第19周 面积计算

第二十周 面积计算（三）专题简析：对于一些比较复杂的组合图形，有时直接分解有一定的困难，这时，可以通过把其中的部分图形进行平移、翻折或旋转，化难为易。

有些图形可以根据“容斥问题“的原理来解答。

在圆的半径r 用小学知识无法求出时，可以把“r 2”整体地代入面积公式求面积。

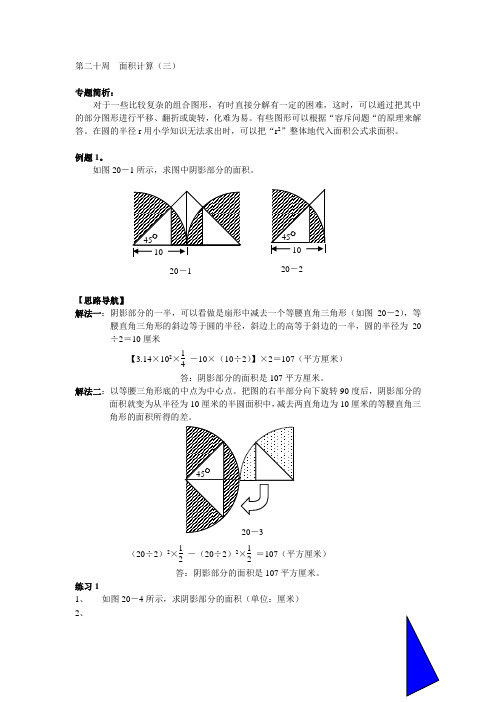
例题1。

如图20－1所示，求图中阴影部分的面积。

【思路导航】解法一：阴影部分的一半，可以看做是扇形中减去一个等腰直角三角形（如图20－2），等腰直角三角形的斜边等于圆的半径，斜边上的高等于斜边的一半，圆的半径为20÷2＝10厘米【3.14×102×14－10×（10÷2）】×2＝107（平方厘米） 答：阴影部分的面积是107平方厘米。

解法二：以等腰三角形底的中点为中心点。

把图的右半部分向下旋转90度后，阴影部分的面积就变为从半径为10厘米的半圆面积中，减去两直角边为10厘米的等腰直角三角形的面积所得的差。

（20÷2）2×12 －（20÷2）2×12＝107（平方厘米） 答：阴影部分的面积是107平方厘米。

练习11、 如图20－4所示，求阴影部分的面积（单位：厘米）2、20－1 20－2例题2。

如图20－6所示，求图中阴影部分的面积（单位：厘米）。

【思路导航】解法一：先用长方形的面积减去小扇形的面积，得空白部分（a ）的面积，再用大扇形的面积减去空白部分（a ）的面积。

如图20－7所示。

3.14×62×14 －（6×4－3.14×42×14 ）＝16.82（平方厘米） 解法二：把阴影部分看作（1）和（2）两部分如图20－8所示。

把大、小两个扇形面积相加，刚好多计算了空白部分和阴影（1）的面积，即长方形的面积。

3.14×42×14 +3.14×62×14－4×6＝16.28（平方厘米） 答：阴影部分的面积是16.82平方厘米。

2024年五年级数学教学计划第一学期1. 第一单元：整数的认识和应用- 理解整数的定义和联系- 正整数和负整数的认识和比较- 整数的加减法运算和应用- 整数在实际问题中的应用2. 第二单元：小数的认识和运算- 小数的读法和表示法- 小数的大小比较- 小数的加减法运算和应用- 小数在实际问题中的应用3. 第三单元：长方体和体积- 长方体的认识和特征- 长方体的表面积和体积的计算- 长方体在实际问题中的应用4. 第四单元：图形的认识和变换- 平面图形的分类和特征- 三角形、四边形和圆的认识和性质- 图形的旋转、翻转和平移变换- 图形在实际问题中的应用5. 第五单元：数据的收集和表示- 数据的收集和整理- 数据的图表表示（条形图、折线图等）- 数据的分析和解读第二学期1. 第六单元：分数的认识和运算- 分数的概念和表示法- 分数的大小比较- 分数的加减法和乘除法运算- 分数在实际问题中的应用2. 第七单元：几何图形的分类和性质- 平行线、垂直线和相交线的认识和性质- 直角、钝角和锐角的认识和性质- 三角形的分类和性质- 四边形的分类和性质3. 第八单元：算式的解法和应用- 算式的解法（倒序计算、调整计算顺序等）- 算式在实际问题中的应用- 算式解答的合理性判断4. 第九单元：约数和倍数- 正整数的约数和倍数的认识和性质- 使用约数和倍数解决实际问题5. 第十单元：数列的认识和应用- 数列的概念和表示法- 数列的规律和性质- 数列在实际问题中的应用通过以上教学计划，学生将能够全面了解并掌握整数、小数、几何图形、分数、数据统计等数学概念和运算方法，培养学生的逻辑思维、分析问题和解决问题的能力。

同时，将数学与实际生活相结合，让学生能够将所学知识应用于实际问题的解决中，培养学生的数学应用能力。

2024年五年级数学教学计划（二）一、教学目标1. 培养学生对数学的兴趣和探究精神，激发学生学习数学的积极性。

2. 掌握五年级数学基本知识和技能。

面积与周长的概念面积和周长是数学中常见的概念，用于描述几何形状的属性。

它们是解决几何问题和实际应用中不可或缺的工具。

本文将介绍面积和周长的定义、计算方法以及其在日常生活中的应用。

一、面积的概念与计算方法面积是指一个平面内的一部分所占的空间大小。

它通常用单位面积来衡量，如平方厘米（cm²）、平方米（m²）等。

而不同几何形状的面积计算方法是不同的。

1.1 矩形和正方形的面积矩形的面积可以通过长和宽的乘积来计算，即面积等于长乘以宽（A = l × w）。

同样，正方形的面积计算公式也是边长的平方（A = s²）。

1.2 三角形的面积三角形的面积计算需要知道其底和高。

面积等于底乘以高的一半（A = 0.5 × b × h）。

1.3 圆的面积圆的面积计算需要知道其半径。

面积等于半径的平方乘以圆周率π（A = π × r²）。

二、周长的概念与计算方法周长是指封闭几何形状的边长之和。

与面积不同，周长的计算方法主要根据几何形状进行。

2.1 矩形和正方形的周长矩形和正方形的周长可以通过计算四条边的长度之和来得到。

对于矩形来说，周长等于两边长和两边宽的两倍（P = 2 × (l + w)）。

而正方形的周长等于四条边长之和（P = 4 × s）。

2.2 三角形的周长三角形的周长计算需要知道三条边的长度。

周长等于三条边长之和（P = a + b + c）。

2.3 圆的周长圆的周长通常称为圆周。

它可以通过圆的直径或半径与圆周率π的乘积来计算。

周长等于直径乘以π（P = d × π）或者等于半径乘以2π（P = 2 × r × π）。

三、面积与周长的应用面积和周长是数学中重要的概念，它们在日常生活和实际应用中有广泛的应用。

3.1 房地产领域在房地产领域，面积和周长的概念被广泛应用于土地和建筑物的测量与评估。

集体备课主讲教案高三数学（文科）主讲人：申占宝19周一、复习方向把握1.一周复习内容：必修二（立体几何）2．考纲研讨了解空间几何体的结构特征和性质、水平放置的平面图形直观图理解三视图空间几何体的体积表面积掌握空间点线面的平行垂直的判定与性质3.考点梳理一、多面体的结构特征三、简单组合体简单组合体的构成有两种基本形式：一种是由简单几何体拼接而成；一种是由简单几何体截去或挖去一部分而成，有多面体与多面体、多面体与旋转体、旋转体与旋转体的组合体．四、平行投影与直观图空间几何体的直观图常用斜二测画法来画，其规则是：(1)原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴、y′轴的夹角为45°(或135°)，z′轴与x′轴和y′轴所在平面垂直．(2)原图形中平行于坐标轴的线段，直观图中仍平行于坐标轴．平行于x轴和z轴的线段在直观图中保持原长度不变，平行于y轴的线段长度在直观图中变为原来的一半．五、三视图几何体的三视图包括正视图、侧视图、俯视图，分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线．六、柱、锥、台和球的侧面积和体积二、习题配置处理5:40小考试题1．(教材习题改编)以下关于几何体的三视图的论述中，正确的是()A．球的三视图总是三个全等的圆B．正方体的三视图总是三个全等的正方形C．水平放置的正四面体的三视图都是正三角形D．水平放置的圆台的俯视图是一个圆2．(2012·杭州模拟)用任意一个平面截一个几何体，各个截面都是圆面，则这个几何体一定是()A．圆柱B．圆锥C．球体D．圆柱、圆锥、球体的组合体3．下列三种叙述，其中正确的有()①用一个平面去截棱锥，棱锥底面和截面之间的部分是棱台；②两个底面平行且相似，其余各面都是梯形的多面体是棱台；③有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台．A．0个B．1个C．2个D．3个4．(教材习题改编)利用斜二测画法得到的：①正方形的直观图一定是菱形；②菱形的直观图一定是菱形；③三角形的直观图一定是三角形．以上结论正确的是________．5．一个长方体去掉一个小长方体，所得几何体的正视图与侧视图分别如图所示，则该几何体的俯视图为________．三、学生学法指导：（注意问题）1、用斜二测画法画几何体的直观图时，要注意原图形与直观图中的“三变、三不变”． “三变”⎩⎪⎨⎪⎧坐标轴的夹角改变，与y 轴平行线段的长度改变，图形改变；“三不变”⎩⎪⎨⎪⎧平行性不变，与x 轴平行的线段长度不变，相对位置不变.2．对三视图的认识及三视图画法(1)空间几何体的三视图是该几何体在三个两两垂直的平面上的正投影，并不是从三个方向看到的该几何体的侧面表示的图形．(2)在画三视图时，重叠的线只画一条，能看见的轮廓线和棱用实线表示，挡住的线要画成虚线．(3)三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体用平行投影画出的轮廓线．3．对斜二测画法的认识及直观图的画法(1)在斜二测画法中，要确定关键点及关键线段，“平行于x 轴的线段平行性不变，长度不变；平行于y 轴的线段平行性不变，长度减半．”(2)按照斜二测画法得到的平面图形的直观图，其面积与原图形的面积有以下关系： S 直观图＝24S 原图形，S 原图形＝22S 直观图． 4．以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量． 5．多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理． 6．旋转体的表面积问题注意其侧面展开图的应用．7．计算柱、锥、台体的体积，关键是根据条件找出相应的底面面积和高，应注意充分利用多面体的截面和旋转体的轴截面，将空间问题转化为平面问题求解．8．注意求体积的一些特殊方法：分割法、补体法、转化法等，它们是解决一些不规则几何体体积计算常用的方法，应熟练掌握．9．等积变换法：利用三棱锥的任一个面可作为三棱锥的底面．①求体积时，可选择容易计算的方式来计算；②利用“等积法”可求“点到面的距离”10．解决与球有关的“切”、“接”问题，一般要过球心及多面体中的特殊点或过线作截面，把空间问题转化为平面问题，从而寻找几何体各元素之间的关系．11．记住几个常用的结论：(1)正方体的棱长为a，球的半径为R，①正方体的外接球，则2R＝3a；②正方体的内切球，则2R＝a；③球与正方体的各棱相切，则2R＝2a.(2)长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝a2＋b2＋c2.(3)正四面体的外接球与内切球的半径之比为1∶3.12.几何体的侧面积和全面积：几何体侧面积是指(各个)侧面面积之和，而全面积是侧面积与所有底面积之和．对侧面积公式的记忆，最好结合几何体的侧面展开图来进行．13．求体积时应注意的几点：(1)求一些不规则几何体的体积常用割补的方法转化成已知体积公式的几何体进行解决．(2)与三视图有关的体积问题注意几何体还原的准确性及数据的准确性．14．求组合体的表面积时注意几何体的衔接部分的处理．。

圆的面积计算教学内容:义务教育小学教学教科书（西师版）.六年级上册.圆的面积.第19--20页。

教学目标：1.让学生经历圆的面积公式的探索过程，理解并掌握圆的面积计算公式，能计算圆的面积。

2.通过观察，比较和实验，发展学生空间观念，培养学生的归纳能力。

3.让学生通过活动体会到知识与观察生活的关系。

教学重点:使学生理解掌握圆的面积计算方法，并能正确计算圆的面积。

教学难点：理解圆的面积计算方法的推导。

教具准备：圆形纸片和正方形纸片、剪刀、直尺。

教学过程:一、课题引入：让学生说出已学平面圆形的面积计算方法。

引入指示课题，并板书：圆的面积计算。

二、新授：1、教学例1.通过展示、学生观察、分析、归纳，用估测方法，得出：一个圆与以圆的半径为边长的小正方形，圆的面积比四个小正方形的面积和小。

用数方格法：得出：圆的面积比3个小正方形的面积和大。

引导学习归纳出:圆的面积是小正方形面积3倍多一些。

即：半径平方的3倍多一些。

2.教学例2.（1）让学生拿出准备好的圆形纸板，将圆平均分成16份，将圆剪开。

（2）引导学生拼成一个（近似）平行的四边形。

（3）引导学生得出圆的面积计算方法。

讨论得出：圆的面积等于这个平行四边形的面积。

近似平行边形的底，相当于圆的周长的一半。

平行四边形的高相当于圆的半径。

归纳出：圆的面积等于平行四边形的面积。

板书：平行四边形面积＝底X高圆的面积＝圆周长的一半X半径用字母表示：s＝πr × r＝πr²3.引导学生概括出：圆的面积等于半径平方（r²）的3倍多一些。

三、应用:教学例3.修建一个半径是30cm的圆形水池，它的占地面积是多少平方米？学生独立完成，集体订正。

四、全课总结：问：这节课学习了什？学会了吗？五、作业布置：练习五第1.2.题。

板书设计：圆的面积圆的面积是半径平方r²的3倍多一些平行四边形面积=底×高圆的面积=周长一半×半径s＝πr × r＝πr²。

第十九周组合图形的面积专题简析：在组合图形中，三角形的面积出现的机会很多，解题时我们还可以记住下面三点：1，两个三角形等底、等高，其面积相等；2，两个三角形底相等，高成倍数关系，面积也成倍数关系；3，两个三角形高相等，底成倍数关系，面积也成倍数关系。

例题1 如图，ABCD是直角梯形，求阴影部分的面积和。

（单位：厘米）分析按照一般解法，首先要求出梯形的面积，然后减去空白部分的面积即得所求面积。

其实，只要连接AC，显然三角形AEC与三角形DEC同底等高其面积相等，这样，我们把两个阴影部分合成了一个三角形ABC。

面积是：6×3÷2=9平方厘米。

练习一1，求下图中阴影部分的面积。

2，求图中阴影部分的面积。

（单位：厘米）3，下图的长方形是一块草坪，中间有两条宽1米的走道，求植草的面积。

例题2 下图中，边长为10和15的两个正方体并放在一起，求三角形ABC（阴影部分）的面积。

分析三角形ADC的面积是10×15÷2=75，而三角形ABC的高是三角形BCD高的15÷10=1.5倍，它们都以BC为边为底，所以，三角形ABC的面积是三角形BCD的1.5倍。

阴影部分的面积是：7.5÷（1＋1.5）×1.5=45。

练习二1，下图中，三角形ABC的面积是36平方厘米，三角形ABE与三角形AEC的面积相等，如果AB=9厘米，FB=FE，求三角形AFE的面积。

2，图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。

3，图中三角形ABC的面积是36平方厘米，AC长8厘米，DE长3厘米，求阴影部分的面积（ADFC不是正方形）。

例题3 两条对角线把梯形ABCD分割成四个三角形。

已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？（单位：平方厘米）分析1，因为三角形ABD与三角形ACD等底等高，所以面积相等。

因此，三角形ABO的面积和三角形DOC的面积相等，也是6平方厘米。

面积和周长的推算技巧在日常生活中，我们经常需要计算物体的面积和周长。

无论是建筑设计、土地测量还是日常生活中的购物和装修，面积和周长的计算都是必不可少的技巧。

本文将介绍一些简单而实用的推算技巧，帮助读者更加高效地计算面积和周长。

一、面积的推算技巧1. 矩形和正方形的面积计算对于一个矩形或正方形，我们可以利用简单的公式来计算其面积。

矩形的面积等于长乘以宽，正方形的面积等于边长的平方。

例如，一块长为5米、宽为3米的矩形地板的面积等于5米乘以3米，即15平方米。

2. 三角形的面积计算计算三角形的面积可以使用海伦公式或直角三角形的特殊公式。

对于已知三边长度的任意三角形，可以使用海伦公式：面积等于根号下（p(p-a)(p-b)(p-c)），其中p为半周长，即p=(a+b+c)/2，a、b、c分别为三角形的三边长度。

对于直角三角形，面积等于直角边的乘积的一半。

例如，一个直角三角形的直角边长度分别为3米和4米，那么其面积等于3米乘以4米的一半，即6平方米。

3. 圆的面积计算计算圆的面积可以使用πr²的公式，其中π取近似值3.14，r为圆的半径。

例如，一个半径为5米的圆的面积等于3.14乘以5米的平方，即78.5平方米。

二、周长的推算技巧1. 矩形和正方形的周长计算矩形的周长等于两倍的长加两倍的宽，正方形的周长等于4倍的边长。

例如，一个边长为4米的正方形的周长等于4米乘以4，即16米。

2. 三角形的周长计算计算三角形的周长可以将三边长度相加。

例如，一个三角形的三边长度分别为3米、4米和5米，那么其周长等于3米加4米加5米，即12米。

3. 圆的周长计算计算圆的周长可以使用2πr的公式，其中π取近似值3.14，r为圆的半径。

例如，一个半径为5米的圆的周长等于2乘以3.14乘以5米，即31.4米。

三、应用技巧1. 分割法当面积或周长无法直接计算时，可以将复杂的形状分割成简单的几何图形，然后计算每个简单图形的面积或周长，最后将结果相加。