矩形截面波导管壁电流分析

引言 金属波导中电磁场解的一般形式 矩形截面波导场方程的求解 矩形截面波导传输模式 矩形截面波导中的TE10模 矩形截面波导的工程应用
一 引言
波导管作为定向导引电磁波传输的机构， 是微波传输线的一种典型类型，它已不再 是普通电路意义上的传输线。虽然电磁波 在波导中的传播特性仍然符合本书第二章 中关于传输线的概念和规律，但是深入研 究导行电磁波在波导中的存在模式及条件， 横向分布规律等问题，则必须从场的角度 根据电磁场基本方程来分析研究。
mπ 2 nπ 2 2 β 2 = ω 2 ε ( k x2 + k y ) = ω 2 ε + a b mπ 2 nπ 2 kc2 = + = ωc 2 ε a b fc = 1 2π ε 1 m n + 2 a 2b
三 矩形截面波导场方程的求解
矩形截面波导结构和坐标如图所示，结构 参数内腔宽a和高b，电磁参数：腔内填充 介质介电常数和磁导率。 求解思路：先求纵场，再求横场。
y
b 0 z
、 ε
x a
矩形截面波导结构和坐标图
1 纵场满足方程和边界条件 很容易推导纵向场所满足的方程如下， TE波中Ψ表示磁场，TM波中Ψ表示电场。
模式存在的条件
对于一种模式，并不是所有的频率电磁波 都能以这种模式存在，或者说每一种模式 存在是有条件的。 这个条件就是这种模式一定能以行波的形 式在波导中传播。 相位常数是实数，其模平方要大于0。
β >0
2
截止频率和截止波长
根据相位常数和模式之间的关系，一种频率 电磁波能在矩形波导中以一种模式传播，则 其频率要大于某一个临界值，这个临界值称 为这种模式存在的截止频率。 截止频率对应波长称为截止波长，截止频率 和截止波长的乘积数值上等于电磁波在波导 填充介质为无界时的相速度。 根据模式截止特性容易判定矩形波导具有高 通的选频特性。

在矩形波导作为传输线运用时，功率容量和衰减是 一个问题的两个方面。功率容量是为了使通信和雷达 “看”得远，减小衰减是为了保证功率不受损失，一个 “增产” ，一个“节支” ，相互依存，缺一不可。
(五)矩形波导的主模—TE10模
由式(2.50)得
PTE10
A2 a3bZ TEM

2
1 2a (2.66a)
(三)场结构和管壁电流分布
(6)波导横截面内电、磁力线疏密分布相间(体现的是驻波 特性)，纵剖面内电、磁力线疏密分布同位(体现的是行波 特性)。
(7)波导中两大系列(TE、TM)波无穷多种模式(TEnm、 TMnm)的场分布可视为m、n取最小值时基本模式场图的组 合。
(五)矩形波导的主模—TE10模
(三)场结构和管壁电流分布
(3)遵循边界条件，理想导体波导壁处电场切向分量应为0， 则电力线应垂直于波导壁而生存，由规律(2)知磁力线必平 行相切于波导壁而生存。 (4)波导壁传导电流(称为壁电流)分布由 n Ht 确定，其中 n为波导壁面向场区一侧的外法向，Ht为壁处切向磁场分 布。 (5)波导空间磁力线始终自身闭合(因自然界不存在磁荷， 磁力线环绕传导或位移电流生存)，电力线既有始于又终 止于波导壁而生存(壁处有表面电荷，体现电场的有散性) 的形式，也有闭合力线(体现时变场中电场的有旋性 E j B )
2ห้องสมุดไป่ตู้
(2.62) (2.64)
g

1 2a
k
2
vg v 1 2a
(2.65)
v
Z TE10

Z TEM
c
r r
(三)场结构和管壁电流分布 可见TE10模只有三个场分量存在，一个电场分量和两 个磁场分量。这里，将场的空间分布图形用z=0处的xy剖 面、x=a/2处的yz剖面和y=b/2处的xz剖面上的分布图表示。 并取瞬时进行作图，首先作三个剖面上的电场分布图。

H10(即TE10）波的截止波长最大，它最容易在波导中传播。
为了保证单一的H10波传输，波导尺寸必须满足：
(c ) H20 (c ) H10
a 2a
(c ) H01
2b
§2.2 矩形波导
2.2.4 矩形波导的主模—TE10
1.场表达式
Ez 0
电力线只分布在波导的横截面内
基模：TE10(a>b)
a
横截面图
y z
Hx 窄边纵切面 Ey
§2.2 矩形波导
x z
g
立体图见图2-5
基模：TE10(a>b) 宽边纵切面
§2.2 矩形波导
3.传输参量
波导波长
g
vp f
1 ( / c )2
相移常数
2 2 g
1 ( / c )2
§2.2 矩形波导
相速
vp
v
1 ( / c )2
群速 vg v 1 ( / c )2
（3） 场量沿z轴为行波，沿x轴和y轴为纯驻波
（4） 主模：最低次模
TE10模
一般来说，用a表示波导宽边，b表示窄边，a>b，K10=π/a是所 有波型中波数最小的，因此TE波型的最低次波型是TE10模。
§2.2 矩形波导
3.传输条件
波导中不同模式的截止波长是不同的，对于特定尺寸的波导，
只有满足 c 的模才能得到传输。
§2.2 矩形波导
TE10单模传输条件：
a 2a
2b
兼顾所能够承受一定的传输功率：图(2-8)
a 1.8a
(2-97)
兼顾最小功率损耗：
a=0.7λ
b=(0.4～0.5)a
§2.2 矩形波导

令（-U0/a）=E0
E y E0 sin a j ( t z ) Hx E0 sin x e a 1 j ( t z ) Hz j E0 cos x e a a x e j ( t z )
j (t z ) Jx x j a E0 cos a x e
k 2 k
1 2 2 c

2 2 2 m n a b
1 2
H T I ( z ) T ( x, y )
ET U ( z ) T ( x, y ) z
X ( x) C1 cos k x x C 2 sin k x x Y ( y ) C3 cos k y y C 4 sin k y y
( x, y) (C1 cosk x x C2 sin k x x)(C3 cosk y y C4 sin k y y)
§3－5矩形波导
一、矩形波导中传输波型 及其场分量
• （一）TM波（Hz=0）
2 ( x, y) 2 ( x, y) k c2 ( x, y) 0 x 2 y 2
(x,y)=X(x)Y(y)
1 d 2 X ( x) 1 d 2Y ( y ) 2 k c 2 2 X ( x) dx Y ( y) dy
j (t z ) Jz z E0 sin a x e JS x
y b
j (t z ) n H t y x H x z H x z E0 sin a x e y b j (t z ) J z x e

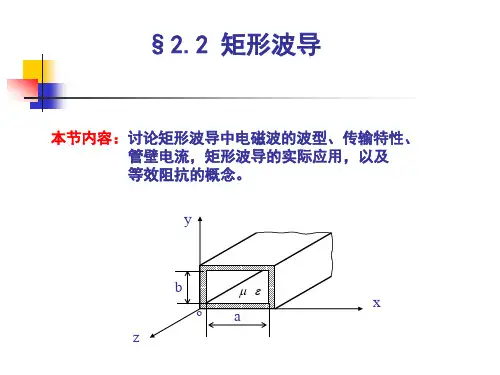
矩形波导的设计讲解矩形波导模式和场结构分析第⼀章绪论1.1选题背景及意义矩形波导(circular waveguide)简称为矩波导，是截⾯形状为矩形的长⽅形的⾦属管。

若将同轴线的内导线抽⾛，则在⼀定条件下，由外导体所包围的矩形空间也能传输电磁能量，这就是矩形波导。

矩波导加⼯⽅便，具有损耗⼩和双极化特性，常⽤于要求双极化模的天线的馈线中，也⼴泛⽤作各种谐振腔、波长计，是⼀种较常⽤的规则⾦属波导。

矩波导有两类传输模式,即TM 模和TE 模。

其中主要有三种常⽤模式，分别是主模TE 11模、矩对称TM 01模、低损耗的TE 01模。

在不同⼯作模式下，截⽌波长、传输特性以及场分布不尽相同，同时，各种⼯作模式的⽤途也不相同。

导模的场描述了电磁波在波导中的传输状态，可以通过电⼒线的疏密来表⽰场得强与弱。

本毕业课题是分析矩形波导中存在的模式、各种模式的场结构和传播特性，着重讨论11TE 、01TE 和01TM 三个常⽤模式，并利⽤MATLAB 和三维⾼频电磁仿真软件HFSS 可视化波导中11TE 、01TE 和01TM 三种模式电场和磁场波结构。

1.2国内外研究概况及发展趋势由于电磁场是以场的形态存在的物质，具有独特的研究⽅法，采取重叠的研究⽅法是其重要的特点，即只有理论分析、测量、计算机模拟的结果相互佐证，才可以认为是获得了正确可信的结论。

时域有限差分法就是实现直接对电磁⼯程问题进⾏计算机模拟的基本⽅法。

在近年的研究电磁问题中，许多学者对时域脉冲源的传播和响应进⾏了⼤量的研究，主要是描述物体在瞬态电磁源作⽤下的理论。

另外，对于物体的电特性，理论上具有⼏乎所有的频率成分，但实际上，只有有限的频带内的频率成分在区主要作⽤。

英国物理学家汤姆逊(电⼦的发现者) 在1893 年发表了⼀本论述麦克斯韦电磁理论的书,肯定了矩⾦属壁管⼦(即矩波导) 传输电磁波的可实现性, 预⾔波长可与矩柱直径相⽐拟, 这就是微波。

他预⾔的矩波导传输, 直到1936 年才实现。

(3-4)
1E P= ab 4η
2 0
空气波导
µ =120π ε
非磁介质波导 µ = µ0 ,ε = ε0εr
E ab λ P= 1− 2a 480π
2 0
2
P=
2 E0 ab εr
ห้องสมุดไป่ตู้480π
λ 1− 2a
2
λ 请注意：对非磁介质波导， = 请注意：对非磁介质波导，
ωµ π
β π
TE10波主要特性
传 条 播 件 波 波 导 长
λ＜ c = 2a λ λ λg = 2 λ
1− 2a C λ 1− 2a 1 λ 1− 2a
2 2
相
速
υp =
波 阻 型 抗
η=
µ ε
场结构
图 3-1
二、TE10波的另一种表示
$ dσ = kdxdy。
v
y
ds z x b a 0
图 3-2
计算功率时的面积元
2 v v 1 E0 2 π S ⋅ dσ = sin xdxdy 2η a 2 1 E0 a b 2 π P= ∫0 ∫0 sin a xdxdy 2η 2 1 E0 a π = b∫ 1− cos xds 2η 0 a
我们在上面给出的TE 波表达式， 我们在上面给出的 TE10 波表达式 ， 是以 Hz 为领矢 矢量的。然而， 作领矢矢量， 矢量的。然而，在实用上也常有用Ey作领矢矢量，即 设 π − jβz Ey = E0 sin x e (3(3-1) a 利用Maxwell方程 方程 利用
2 Htmdl s
(3-9)
其中， 其中，

实验二 矩形波导仿真与分析一、实验目的：1、 熟悉HFSS 软件的使用；2、 掌握导波场分析和求解方法，矩形波导高次模的基本设计方法；3、 利用HFSS 软件进行电磁场分析，掌握导模场结构和管壁电流结构规律和特点。

二、预习要求1、 导波原理。

2、 矩形波导模式基本结构，及其基本电磁场分析和理论。

3、 HFSS 软件基本使用方法。

三、实验原理由于矩形波导的四壁都是导体,根据边界条件波导中不可能传输TEM 模,只能传输TE 或TM 模。

这里只分析TE 模(Ez=0)对于TE 模只要解Hz 的波动方程。

即采用分离变量，并带入边界条件解上式，得出TE 模的横向分量的复振幅分别为（1）矩形波导中传输模式的纵向传输特性①截止特性波导中波在传输方向的波数β由式9 给出222000220z z c z H H k H x y ∂∂++=∂∂式7000220002200020002()cos()sin()()sin()cos()()sin()cos()()cos()sin()z x c c z y c c y x H c x y H c H n m n E j j H x y k y k b a b H m m n E j j H x y k x k a a b E m m n H j H x y Z k a a b E n m n H j H x y Z k b a b ωμωμπππωμωμπππβπππβπππ∂⎧==⎪∂⎪⎪∂==-⎪∂⎪⎨⎪=-=⎪⎪⎪==⎪⎩式822222c c k k ππβλλ=-=-式9式中k 为自由空间中同频率的电磁波的波数。

要使波导中存在导波,则β必须为实数,即k 2＞k 2c 或λ＜λc(f ＞f c ) 式10如果上式不满足,则电磁波不能在波导内传输,称为截止。

故k c 称为截止波数。

矩形波导中TE 10模的截止波长最长,故称它为最低模式,其余模式均称为高次模。

由于TE 10模的截止波长最长且等于2a,用它来传输可以保证单模传输。

m 场量沿x轴[0,a]出现的半周期（半个纯驻波）的数目；
n 场量沿y轴[0,b]出现的半周期的数目。
④j 相位关系 Ey－Hx、Ex－Hy
z轴有功率传输
Ez－Hx、Ez－Hy
x、y轴无功率传输
所以行波状态下，沿波导纵向（z轴）传输有功功率、横向（x、
y轴）无功功率。
2) 场结构
为了能形象和直观的了解场的分布（场结构），可以 利用电力线和磁力线来描绘它。电力线和磁力线遵循 的规律：
力线上某点的切线方向
该点处场的方向
力线的疏密程度
场的强弱
电力线 发自正电荷、止于负电荷，也可以环绕着交变磁场构 成闭合曲线，电力线之间不能相交。在波导壁的内表面（假设为 理想导体）电场的切向分量为零，只有法向分量（垂直分量）， 即在波导内壁处电力线垂直边壁。
磁力线 总是闭合曲线，或者围绕载流导体，或者围绕交变电 场而闭合，磁力线之间不能相交，在波导壁的内表面上只能存在 磁场的切向分量，法向分量为零。
3）相速和群速
TMmn和TEmn波型的相速和群速表示式相同：
vp
v
1(/c)2
vg v 1－c2
4）波型阻抗
TMmn和TEmn波型阻抗为：
ZTE
1
1c2
g
ZTM
1c2
g
5）尺寸选择——矩形波导的工作波型图
基于前面的定义，根据波导横截面尺寸、工作波长、 截止波长之间关系，构成矩形波导工作波型图。根据不 同要求，可利用波型图对波导的横截面尺寸和波导波长 作出选择。
TE0n和TEm0是非简并模；其余的TEmn和TMmn都存在简并模: 若a=b， 则TEmn 、TEnm、TMmn和TMnm是简并模；若a=2b，则TE01与TE20，TE02和 TE40，TE50、TE32和TM32是简并模。

整理ppt
6
管壁电流的求解：
J H （1）
n
s
i
n为波导内壁面的法线方向单位矢量 Hi为波导内壁面上切线方向磁场
TE10模的磁场表达式：
（2）
H ZH 0CO (a S x)
H xj aH 0sin a x ()
整理ppt
7
管壁电流的分布
由（1）式知，只要知道波导表面切向磁场的分布，就可得出管壁电流分布， 通过对各个方向电流的求解，分析出与TE10模相对应的波导内壁上一瞬间的 壁电流分布形态。
管壁电流相反，电流密度既有z 分量，也有x分量，电流密度是x 的函数
10
根据对各个方向管壁电流值得分析得出如下管壁电流分布形态图
对于不同的传输模式，都有其各自对应的壁电流分布。从所画出的TE10模电流的分 布形态可以看出，波导内壁面上的电流似乎在流入流出位置上发生中断，实际上它 是靠着相对壁面间的位移电流连续的。
整理ppt
1
目
1 矩形金属波导
录
2 矩形金属波导在主模TE10模下电磁场
3 管壁电流分布
4
开槽问题
整理ppt
2
矩形金属波导
由金属材料制成的、矩形截面的、 内充空气介质的规则金属波导的统称。
结构简单，机械强度大，其封闭的结构 可以避免外界干扰和辐射损耗，又因为 它无内导体，所以导体损耗低，功率容 量大。
整理ppt
11
开槽问题
若窄缝是沿电流取向，它将不会影响或极少影响场强的分布； 若窄缝切断了管壁电流，则场型将被扰乱，其结果将会引起辐 射和管内波的反射等现象。
非辐射性槽
整理ppt
辐射性槽
12
目前的大功率的微波系统中常采用矩 形波导作为传输线和构成微波元器件。

复习
1. 矩形波导各个模型的截止波长？
2. a>2b和a<2b情况下，矩形波导的第一高次 模分别是什么？ 3.矩形波导有哪几种兼并模式？
4.TE10、TE01、TE11横截面的场结构图？ 下次课交作业
2.2 矩形波导
一. 矩形波导
(一)场分量 (二)模式分布与简并
(三)场结构和管壁电流分布
(四)传输功率、能量和衰减 略
JS JS JS JS
x 0 x a
ax H z
x 0
a y A10 e
j t z
ax H z
x a
a y A10 e j t z
y 0
ay H x H z
y b
a a j j t z j t z a y H x H z az A10 sin x e ax A10 cos x e y b a a
(三)场结构和管壁电流分布 (1)取图2.11(b)中TE10模的磁场结构，设想将波导在b处分 开，展开成平面，内表面在上方，其各表面处的磁力线分 布如图2.18(a)中的虚线所示。 (2)根据电流线和磁力线正交，方向由 n H J s 的右螺 旋关系确定，作出电流分布如图2.18(a)中的实线所示。
综上所述，矩形波导各模的场结构中，只有 TE10 、 TE01、TE11和 TM11四种模的场结构是最基本的。它们是 更高次模场结构的基础结构，只要掌握了这四种模的场 结构，其他模的场结构便全明白了。
(三)场结构和管壁电流分布
和同轴线一样，由于波导中导波电磁场感应，波导 内壁上存在有高频电荷与电流。仿照同轴线的方法，将 波导各内壁处切向磁场分量代入 n H＝J s 式中可求得 各壁上的表面电流分量表达式。根据表面电流表达式或 直接根据导体表面的磁场结构可以作出电流分布图形。 下面以TE10模为例，直接由表面磁场结构作出波导的壁 电流分布图。

矩形波导管中的TE11模电磁波及管壁电流作者：赵春然朱孟正公丕锋张金锋来源：《牡丹江师范学院学报（自然科学版）》2019年第04期摘;要：给出矩形波导管中电磁波的电场和磁场各分量表达式，并分析管内传输的电磁波的特性，重点讨论管中仅传输TE11模波的情况.采用数值计算的方式，描绘对应的场结构以及管壁上的面电流、磁场以及电场分布.关键词：电磁波;波导;面电流密度[中图分类号]O451 ;;;[文献标志码]AExploring TE11 Mode Electromagnetic Wave in aRectangular Waveguide and Wall-currentZHAO Chunran， ZHU Mengzheng， GONG Pifeng， ZHANG Jinfeng（School of Physics and Electronic Information，Huaibei Normal University，Huaibei 235000，China）Abstract：The electric field and magnetic field component expressions of the electromagnetic waves in the rectangular waveguide are given. The characteristics of the electromagnetic waves transmitted in the waveguide are analyzed. This paper focuses on the transmission of only the TE11 mode in the waveguide， using numerical calculations to depict the corresponding field structure and the wall-current， magnetic field and electric field distribution on the tube wall of waveguide by numerical calculation.Key words：electromagnetic waves; waveguide; surface current density在低頻或直流电传输时，通常采用双线传输.随着传输电流频率的提高，采用双线就会出现以下缺点：双线会把所传输的电磁能向周围空间辐射，具有天线的作用;双线传输的导体裸露在外，它本身既相当于一个辐射天线，又相当于一个接收天线，会接收空间的杂散电磁波;双线的分布电容不能忽略，以致会出现部分短路.为了克服双线的上述缺点，当需要传输较高频率的电磁能时，利用导体对电磁波的屏蔽作用，把一根导线展成柱面，使它把另一根导线包围起来.由于柱面导体的屏蔽，较高频率的电磁波不会向四周辐射，外界的干扰信号也不会进到中芯线.当频率更高时，导体中电磁波的穿透深度减小，电流通过的有效截面积减小，因而电阻增大，这一点对同轴线内导体的影响尤为突出，为了克服上述缺点，人们逐渐抛弃了内导体，只有一个空心导体管的波导诞生了.1;矩形波导中电磁波理想导体构成的波导管，其矩形横截面的两边长为a和b，如图1所示.电场的空间分量可令为：E（x）=E（x，y，z）=E（x，y）rikzz.（1）对于一定频率的电磁波，场矢量的空间分量应满足：SymbolQC@2E+k2E=0B=-iωSymbolQC@×ESymbolQC@·E=0;.（2）将波导管壁看作由理想导体构成，则根据边界条件有：n×E（x）=0，（3）即，在导体表面附近的电场线与界面正交.[6]由方程组（2）中的第一个方程解的结果还必须满足第三个方程，以及条件式，得另一个边界条件：En（x）n=0.（4）利用边界条件（3）（4）式，从而对（2）式作出限定，矩形波导管中电场的各分量，并考到是时谐变化的：Ex=E0xcoskxxsinkyyei（kzz-ω t），Ey=E0ysinkxxcoskyyei（kzz-ω t），（5）Ez=kxE0x+kyE0yikzsinkxxsinkyei（kzz-ω，t）.其中，kx=mπ/a，ky=nπ/b，m，n=0，1，2，….M，n分别代表a边、b边所含的半波数目.由方程组（2）的第二个方程及（5）式得磁场的表达形式：Bx=-1ω k[kxkyE0x+（ky2+kz2）E0y]sinkxxcoskyyei（kzz-ω t），By=1ω k[（kx2+kz2）E0x+kxkyE0y]coskxxsinkyyei（kzz-ω t），（6）Bz=-iω（kxE0y-kyE0x）coskxxcoskyyei（kzz-ω t）.从描述波导管内电磁场量的（5）式和（6）式可以看出：（1）电磁波沿波导管长度方向上为行波，在矩形波导管的横截面上的两个方向上为驻波.（2）管中电场和磁场不可能同时为横波.假设管中电场和磁场同时为横波，即Ez=0，Bz=0，则得到：E0x=0，E0y=0.这个结果说明管中无电磁波存在，显然矛盾！若管中Ez=0，则称为横电波（TEmn）;若管中Bz=0，则称为横磁波（TMmn）.（3）波导管中存在截止频率，对于波矢量有：kz2=k2-（kx2+ky2）=ω2μ ε-[（mπa）2+（nπb）2].（7）若kz2ωc，mn=πμε（ma）2+（nb）2（8）称为截止频率，相应的截止（最大）波长：λc，mn=vT=1μ ε2πωc，mn .（9）（4）笔者注意到，（9）式中1/με并非是波导管中电磁波的相速度.由传播因子ri（kzz-ωt）很容易得到导行波的相速度，其等相面方程为kzz-ω t=常数，由此得相速度：vp=dxdt=ωkz>1μ ε .（10）若波导管是真空，则vp>c，按相对论，信号的传播速度绝不能超过光速c，这意味着相速度不能承当信号的传播速度.事实上能够很容易看出，相速度不能从实验上测定，因此它缺乏任何直接物理意义.（5）波导波长λg是指某一频率的导行波等相面在一个周期内沿轴向移动的距离.λg=vpT=2πkz>2πk .（11）而k=ωμε为波源的波数，则波源的波长λ=2π/k，λ代表频率为ω的波源在无限均匀介质的自由空间中传播时的波长，所以波长λ与介质的性质有关.（6）波导管中导行电磁波的群速度.实际中输入的波不可能是完全单色的，其频率总有些微小差别，因此，不同频率的波列叠加形成波群（波包），波群的等振幅面向前传播的速度称为群速度.故此，矩形波导管中电磁波群速度为：vg=dωdkz=kzωμ ε1μ ε由（10）（12）式可以看出，波导管中导行波的相速度vp与群速度vg都和ω有关，这种波称为色散型电磁波.必须指出，导行波的色散是由于波导管壁的边界条件决定的，而光波在透明介质中传播时的色散是由介质的性质引起的，这两种色散物理过程是完全不同的.此外，由（10）和（12）式可得：vpvg=ωkz·kzωμε=1μ ε .2;TE11波的场量及其形成的管壁电流现行绝大多数电动力学[1，3-4]教材涉及这部分内容时，都对TE10波给予了充分的分析，但是对于TE11波的分析少之又少，故此，接下来着重分析矩形波导管中仅存在TE11模时，管内的场结构以及管壁上的面电流分布情况.就TE11模电磁波而言：m=1，n=1，所以：kx=π/a，ky=π/b.（13）横电波要求Ez=0，则：E0x=-aE0y/b.（14）根据（13）式和（14）式表达的条件，针对TE11波的电场部分和磁场部分的各个分量参照（5）式和（6）式就很易得出.利用数值模拟的方法探讨TE11型波的场结构.场结构就是用电场线和磁场线表示的电磁场的空间分布，可以描绘出某一特定时刻的场线空间分布图形，随着时间的推移，整个场线图形将沿z轴方向平移.根据TE11波的电场部分和磁场部分的各个分量，且t=0时刻，取电场和磁场的实部进行数值计算.如图2所示，描绘了TE11型波的场结构，电场用浅色加粗带箭头的线段表示，磁场线用黑色带箭头的线段表示，其带箭头线段的长短代表电场或磁场强度的大小.数值计算中，选择波导管的宽边a=2mm，窄边b=1mm，传输的TE11型波的频率就是截止频率，E0y=1，在传播方向上，即z轴上绘制了一个波导波长.图2中浅色加粗的电场线均平行于xOy平面，参见图1的坐标系，对比文献的结果[2]，TE11型波的场结构显然要比TE10型波的复杂的多.根据电磁场的边值关系，波导管内表面的管壁的面电流密度：α=n×H.（15）在x=0面上，法向矢量n的三个分量很显然可表示为：ny=0，nz=0及nx=1;在x=a面上，ny=0，nz=0及nx=-1;在y=0面上，nx=0，nz=0及ny=1;在y=b面上，nx=0，nz=0及ny= -1.因此很容易得到公式（16）（17）.（1）在x=a面上零时刻的管壁电流：α=-aπE0yμ0ω（1a2+1b2）cosπbysinkzzey-aE0ykzμ0ω bsinπbycoskzzez.（16）（2）在y=b面上零时刻的管壁电流：α=aπE0yμ0ω（1a2+1b2）cosπaxsinkzzex+aE0ykzμ0ωsinπaxcoskzzez.（17）图3;波导管的管壁x=a面上的面图4;波导管的管壁y=b面上的面电流密度、磁场线以及电场分布电流密度、磁场线以及电场分布利用MATLAB软件数值计算方法描绘图1中靠外侧的两个面——波导管的内壁x=a面和y=b面上的面电流、电场线和磁场线.如图3和图4所示，数值计算时所需参数同前面图2提到的一样.浅色加粗带箭头的线段表示面电流密度矢量，相对深颜色带箭头的线段表示磁场强度矢量，线段的长短代表面电流密度或磁场强度的大小;在波导管的内壁x=a面或y=b面上，电场强度矢量与这些面是垂直的，图中用小圆点表示电场强度矢量的方向朝外、叉号表示其方向朝里，因数据采样的等间距性要求，图3和图4中所描绘的小圆点和叉号的分布密度并不能说明相应处的电场强度大小.为弥补这一缺陷，用电场强度的等高图来反映电场在各处强弱分布.管壁上面电流密度α与该管壁面附近的磁场方向垂直，但是在图3和图4中的部分部位可能会发现不垂直，这是图像显示的纵横比导致的.在波导管的内壁x=a面的中线上，沿y轴的面电流为零（图3），表明若在窄边中线上开沿z轴的窄缝，将不会对波导管中的电磁场产生大的扰动，而这种窄缝广泛地应用于用探针测量波导管内物理量的技术中;在波导管的内壁y=b面的中线上，沿x轴的面电流为零（图4），表明若在宽边中线上开沿z轴的窄缝，也不会对波导管中的電磁场产生大的扰动.综上所述，虽然TE11型波的场结构要比TE10型波的复杂很多，但是若想采用探针技术来测量波导管内TE11型波的物理量，仍然是可以找到合适的位置在波导管上开“窄缝”.[1]3;结论给出矩形波导管中电磁波的电场和磁场各分量表达式，并分析了管内传输的电磁波的特性，最后通过MATLAB软件，采用数值计算的方式，讨论了波导管中只传输TE11型波，对应的场结构以及管壁上的面电流、磁场以及电场分布，发现TE11型波的场结构要比TE10型的复杂的多，从管壁上的面电流分布发现：可以在管壁上找到合适的位置开“窄缝”，用于探针测量波导管内电磁波的场量.参考文献[1]郭硕鸿. 电动力学[M]. 北京：高等教育出版社， 2008：131-134.[2]钱尚武. 电磁学要义[M]. 北京：科学出版社， 2009：71-76.[3]张民宽. 电动力学[M]. 开封：河南大学出版社， 1990：197-205.[4]胡友秋，程福臻. 电磁学与电动力学：下[M]. 北京：科学出版社， 2008：116-121.[5]付斯年，朱瑞华，吴春雷，等. 利用波导管的可调终端活塞及单螺调配器测定微波信号源的波长[J]. 牡丹江师范学院学报：自然科学版， 2014（1）：12-13.[6]魏仁怀，朱孟正. 平面电磁波在运动介质界面上折射行为的研究[J]. 牡丹江师范学院学报：自然科学版， 2009（4）：10-12.编辑：琳莉。

s
自 学
§2.2 矩形波导
7.TE10波的波阻抗与等效阻抗
(一) 波阻抗
Z TE 10
1 1 ( / 2 a ) 2
(2-105)
可见TE10波的波阻抗与窄边b的尺寸无关. 因此，如果它完全与传输线的特性阻抗相当，则两个宽边 相等而窄边不等的波导相接时，将无反射存在。 但是实验否定了这一结论。相反这种情况下将发生很大反射。 从而说明：与传输线不同，两个波导的波阻抗并不能保证 它们相匹配。为了寻求波导匹配问题，必须寻求另一个关 于阻抗的量。
§2.2 矩形波导
在y=0宽壁上
J Sz
ˆ (x ˆH x z ˆJ Sx ˆH z ) z ˆJ Sz x J S n H y
a ˆ z H 0 sin( x) cos( t z ) a 2
J Sx
ˆH 0 cos( x
当a=b时，TEmn、TEnm 、TMmn、TMnm是简并波型； 当a=2b时，TE01与TE20 ；TE02与TE40；TE50与TE32；
TEmn、TMmn、是简并波型；等等
唯一的条件:截止波长相等
§2.2 矩形波导
截止频率
f c v / c
1 2
m n a b
ˆE x＋y ˆE y＋z ˆE z 在直角坐标系中，令 E x
则关于E的矢量波动方程分解为三个标量波动方程，
2 2 其中关于Ez的波动方程为： Ez Ez K 2 E 0 c z 2 2
x
y
(2-62)
同理，Hz所满足的标量形式的波动方程为
2H z x 2 2H z y 2
2 Y '' K y Y 0

⎡ ∂ φ ( x, y ) ∂ φ ( x, y ) ⎤ α x H x + α y H y = I ( z )⎢α x + αy × αz ⎥ ∂ x ∂ y ⎦ ⎣
《微波技术》
Harbin Harbin Engineering Engineering University University
3-5 矩形波导
一、矩形波导中传输波型及其场分量 （一）TM波
d2 X ( x ) 2 + k X ( x) = 0 x 2 dx d 2Y ( y ) 2 k + yY ( y ) = 0 2 dy ⎫ ⎪ ⎪ ⎬ ⎪ ⎪ ⎭
Note:
k +k =k
2 x 2 y
2 c
通解为
X ( x ) = C1 cos k x x + C2 sin k x x Y ( y ) = C3 cos k y y + C4 sin k y y
Ez = − j Hz = 0 U sin x ⎟ sin ⎜ y ⎟ e β 0 ⎜ a ⎝ ⎠ ⎝b ⎠ ⎪ ⎪ ⎪ ⎪ ⎭
⎛ mπ ⎞ ⎛ mπ ⎞ ⎛ nπ ⎞ j(ω t − β z ) Ex = −U 0 ⎜ x ⎟ sin ⎜ y⎟e ⎟ cos ⎜ ⎝ a ⎠ ⎝ a ⎠ ⎝ b ⎠ ⎛ nπ ⎞ ⎛ mπ ⎞ ⎛ nπ ⎞ j(ω t − β z ) E y = −U 0 ⎜ ⎟ sin ⎜ x ⎟ cos ⎜ y⎟e ⎝ b ⎠ ⎝ a ⎠ ⎝ b ⎠
截止波数为
⎛ mπ ⎞ ⎛ nπ ⎞ kc = ⎜ ⎟ +⎜ ⎟ ⎝ a ⎠ ⎝ b ⎠
《微波技术》
2 2
Harbin Harbin Engineering Engineering University University

c
2
1
m
2
n
2
a b
§2-3 矩形波导管中电磁波的传输特性——三、矩形波导管中电磁波的传输特性
❖ 简并现象：不同波型具有相同截止波长（或截止频率）的现象
简并波型的kc、fc、vg、vp以及g都是相同的 kc
o 一般情况下： ▪ TE0n和TEm0是非简并模（TM最低次模为TM11）
2 m 2 n 2 a b
矩形波导管管壁电流立体分布图
❖ 左右两侧壁的电流 ❖ 只有Jy分量 ❖ 大小相等，方向相同。
❖ 上下宽壁内的电流 ❖由Jz和Jx合成， ❖ 同一位置上下宽壁内的管壁电流大小 相等，方向相反。
§2-3 矩形波导管中电磁波的传输特性——四、矩形波导管的管壁电流
了解管壁电流的分布情况，对解决某些实际问题有帮助
ax
s
in
2
a
x dxdy
Em2 axb
2ZTE10
a sin 2
0
a
x dx ab
2ZTE10
Em2 ax
§2-3 矩形波导管中电磁波的传输特性——三、矩形波导管中电磁波的传输特性
▪ 功率容量Pbr：波导能够传输（承受）的最大允许功率（极限功率）
Emax Ey xa / 2 Ebr
a 0.7
b 0.4 ~ 0.5a
▪ 使用的波导已标准化：可根据需要选用
§2-3 矩形波导管中电磁波的传输特性——
四、矩形波导管的管壁电流
▪ 导行波在金属波导内壁表面上将感应出高频电流，称为管壁电流。
▪ 管壁电流如何分布？
假定内表面是理想导体， ▪ Js表示内表面上的表面电流密度矢量 ▪ H表示内表面处切线方向的磁场强度 ▪ an表示内表面法线方向的单位矢量

根据边界条件（波导管壁内表面电场切向分量为零）求解 上式中待定常数：
x 0 x a y 0 y b
Ez 0 Ez 0 Ez 0 Ez 0
x 2 K x m a y 2
K y n b
第2章 规则金属波导
则有：
m n E z E0 sin( x) sin( y )e jz a b
第2章 规则金属波导
纵向分量求解： 纵向分量波动方程可写为：
2 Ez 2 Ez K c2 Ez 0 x 2 y 2 2H z 2H z K c2 H z 0 x 2 y 2
采用分离变量法：
（2.3-5) （2.3-6)
EZ X ( x)Y ( y)
X Y K c2 X Y 上式成立必须满足（Kx、Ky为横向截止波数） ：
第2章 规则金属波导
（2）场结构
TM11模场结构图
第2章 规则金属波导
TM21模场结构图
第2章 规则金属波导
(二)TE波 （1）场分量的表示式 此时Ez=0, Hz≠0, 且满足
H z H0 cos(K x x x ) cos(K y y y )e jz
根据边界条件（波导管壁内表面磁场法向分量为零）求解 上式中待定常数：
第2章 规则金属波导
对均不为零的m和n, TEmn 和TMmn 模具有相同的截止波长
和λc截止波数Kc，Kc和λc相同但波型不同称为简并模, 虽然它们
（2.3-16) （2.3-17)
第2章 规则金属波导
二、 矩形波导中的场 由上节分析可知, 矩形金属波导中只能存在TE波和 TM波。下面分别来讨论这两种情况下场的分布。 (一)TM波 （1）场分量的表示式 此时Hz=0, Ez≠0, 且满足

- jwmk y k 0=
2 c
- jwmk x k
2 c
由x=0,y=0边界条件：
0=
( A1 cos k x x + A2 sin k x x) B2 A2 ( B1 cos k y y + B2 sin k y y )
- jwmk x k
2 c
B2 = 0 A2 = 0
由x=a,y=b边界条件及A2=0,B2=0, 可得：
导行波的纵向场分量满足亥姆霍兹方程： 由分离变量法： Ez ( x, y, z ) = E0 z ( x, y)Z ( z) 代入上式并进行分离：
Ñ t E0 z ( x, y ) E0 z ( x, y )
2
ห้องสมุดไป่ตู้
? Ez ? Hz
2
2
k Ez = 0 k Hz = 0
2
2
d
2 2
+ dz Z ( z)
式中
骣p 骣p m n 2 2 2 珑 鼢+ kc = k x + k y = 珑 鼢 珑a 鼢 桫 桫 b
2
2
有无穷多TE导模，TEmn表示。最低TE10模。 注： 对于m=0, n=0的解无意义。
并由前式：
kc = k - b
2
2
2
k = w me =
2p l
(2) TM模 对于TM模：
Ez ? 0, Hz 0
x cos
np b
ゥ
y=
邋
n = 0 m= 0
H 0 mn cos
mp a
x cos
np b
y
对于三维变量，其通解为：
ゥ
H z ( x, y , z ) =

Ey Ez Hx

m 1 n 1


j n mx ny j (t z ) E mn sin cos e 2 a b kc b mx ny j (t z ) E mn sin sin e a b j n mx ny j (t z ) E mn sin cos e 2 b a b kc j m mx ny j (t z ) E mn cos sin e 2 a a b kc
如为虚数，令j=a, 则有 EZ=E0Ze-az为衰减波，在波导中为：
2 v c kc f c
2
m / a n / b
2
2
2
则可得截止频率为：
fc v 1 1 m n m n c 2 2 a b 2 a b kc
代入纵横关系式，可得传输型TE模场分量(P52)：
Ex Ey
m 0 n 0



j n mx ny j (t z ) H mn cos sin e 2 b a b kc
j m mx ny j (t z ) H mn sin cos e 2 a a b kc m 0 n 0
式中
k
2 c
k
2
2
由于波导中不存在TEM波，故只有TE波和TM波。
1）TE模
E z 0, H z 0
磁场的纵向分量应满足本征值方程：
2 抖H 0 z + 2 抖 x 2
H0z + kc2 H 0 z = 0 y2
对于 H 0 z ( x, y ) 应用分离变量法求解：
H 0 z ( x, y ) X ( x)Y ( y )