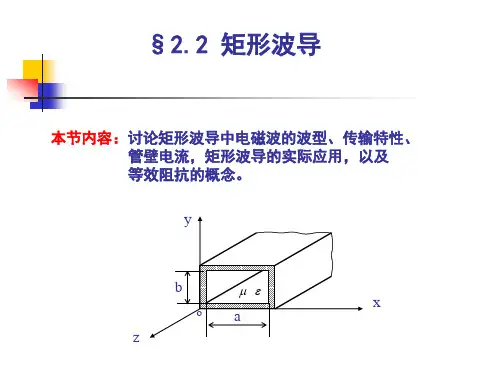
本节主要内容矩形波导中的场不同模式的场结构GG 场分解为(transverse field)zz t z z t H a H H E a E E G K +=+=横向场(transverse field)和纵向场(longitudinal field)z z z y x H z y x H y x E z y x E ββj 0j 0e),(),,(e),(),,(−−==⎟⎟⎠⎞⎜⎜⎛∂∂+∂∂−=x E y H k E z z x βωμ2j ⎟⎟⎞⎜⎜⎛∂∂−∂∂=⎝E x H k E z z y βωμ2c j ⎟⎟⎠⎞⎜⎜⎛∂+∂−=⎠⎝y E x H H y z z x ωεβ2c j ⎟⎟⎞⎜⎜⎛∂+∂−=⎝∂∂E H H k z z y ωεβ2c j ⎝k c，系统将不存在任何场。
全为零，系统将不存在任何场。
一般情况下，只要E z 和H z中有一个不为零即可满足边界条件，这时又可分为二种情形：，这时又可分为种情形横电波（TE波）横磁波（TM波）220),(),(=+∇y x H k y x H oz coz t 222∂+∂=∇22t y x ∂∂直角坐标系中，0)y ,x (H )k (oz 2c 2222=+∂∂+∂yx ∂)y (Y )x (X )y ,x (H oz =122222()1()()()cd X x d Y y k X x dx Y y dy−−=0)x (X k )x (X d 2x 22=+222cyxkk k =+令：yx xz++=TE波的纵向场的通解为y|0Zs H ∂=0|H |H b y z0y z =∂=∂==n∂磁场强度法向分量=0yy ∂∂0xk cos A x k sin A ax ,0x x 2x 1=+−==磁场强度法向分量00|xH |x H a x z0x z =∂∂=∂∂==0A 2=am k x π=yk cos B y k sin B by ,0y y 2y 1=+−==0B 2=n πbk y =2cos()sin()j zx mn j n m n E H x y e βωμπππ∞∞−=∑∑k b a a==j zj m m n E H βωμπππ∞∞−−=sin()cos()y mn m n c x y ek a a a ==∑∑n (m i (H m j πππ−∞∞zj mn 0m 0n 2c x e )y acos()x a sin(a k H ββ==∑∑=m j ∞∞zj mn 0m 0n 2cy e)y a n sin()x a m cos(H b k H βπππβ−==∑∑==00(,,)cos()cos()j zz mn m n m n H x y z H x y e a b βππ∞∞−===∑∑矩形波导TE波的截止波数以TE TE mn 表示和n不能同时为零,否则成为恒定磁场.¾最低次波型为TE 10（a>b）,截止频率最低m和n不能同时为零, 否则成为恒定磁场. m ——表示x 方向变化的半周期数n ——表示y 方向变化的半周期数β−⎛z z e)y ,x (E E ,=0TM 波：H z =00,(,)|0oz y y b E x y ===∑∑∞∞∞=∞=−⎞⎟⎠⎞⎜⎝⎛⎟⎠⎞⎜⎝=11j eπsin πsin m n zmn z y b n x a m E E β∑∑∞∞==−−⎟⎠⎜⎝⎛⎟⎠⎞⎜⎝⎛−=11j 2ceπsin πcos πj m n zmn x y b n x a m E a m k E ββ0,(,)|0oz x x a E x y ===∑∑∞∞==−⎞⎟⎠⎞⎜⎝⎛⎟⎠⎞⎜⎝⎛=11j 2ci eπcos πsin πj m n zmn y E n j y b n x a m E b n k E ββ∑∑∞∞==−−⎟⎠⎜⎝⎛⎟⎠⎞⎜⎝⎛=11j 2c πππeπcos πsin πm n zmn x n m m y bn x a m b k H βωεωε⎞⎛⎞⎛j论TM11模是矩形波导TM波的最低次模，其它均为高模式场的总和。
