压电效应与压电方程

格式：ppt
大小：507.51 KB
文档页数：99

下载文档原格式

压电效应

石英晶体的压电效应
第‹#› 页
26.05.2020
现分别进行如下实验：
（1）当晶片受到沿x轴方向的力Fx作用时，通过冲击电流计，可测出在x轴方向电极面上的电荷q(1)1。并发现x轴方向电极面上的电荷密度（q(1)1/llw）的大小与x轴方向单位面积上的力（Fx /llw）成正比，即：
q (1) 1
P 2 E 0 ( d 2 5 X 5 d 2 6 X 6 ) ( d 1 4 X 5 2 d 1 1 X 6 ) （4-7）
• 振动模式：
– 振动模式、压电振子的等效电路、机电类比和机电网络
• 谐振器和振荡器：
– 谐振器的等效电路、振动模式；振荡器原理
石英晶体的压电效应
第‹#› 页
26.05.2020
压电效应 Piezoelectric effect
• 压电效应 (Piezoelectric effect)：是指材料在压力作用下产生与压力成正比的电荷量，正压电效应；或者在电压作用下，材料发生与电压成正比的机械形变量，逆压电效应。压电效应由压电方程描写；材料的压电性由压电常数决定。并不是所有材料都具有压电性，只有满足一定对称性的晶体材料才会有压电效应。
第‹#› 页
26.05.2020
—石英晶体属于六角晶系32点群，坐标系o-xyz。
石英晶体的压电效应
第‹#› 页
26.05.2020
在晶体x轴垂直的方向上，切下一块薄晶片，晶片面与x轴垂直，如图4-1b所示，称为x切割。更详细的说法是：如果晶片的厚度沿x轴方向，长度沿y方向，则称为xy切割。该晶片的长度为l，宽度为lw，厚度为lt，与x轴垂直的二个晶面上涂上电极，并与冲击电流计连接(测量电量用)，如图4-1c所示。

压电陶瓷的压电原理及制作工艺

极化
在强电场的作用下，使陶瓷内部产生电畴，即压电效应的微观结构。
老炼
在高温和高电压下对极化后的陶瓷进行长时间的老炼处理，以进一步提高其性能。
05
压电陶瓷的发展趋势与展望
高性能化
高压电电压常数
随着科技的发展，对压电陶瓷的电压常数要求越来越高，以提高
其转换效率和应用范围。
高机械品质因数
机械品质因数是衡量压电陶瓷性能的重要参数，提高其数值有助于降低能量损耗，提高陶瓷的稳定性。源自电学品质因数总结词
电学品质因数反映了压电陶瓷的介电能与机械能之比，是评价其能量转换效率的重要参数。
详细描述
高品质的压电陶瓷具有较高的电学品质因数，意味着其介电能转换为机械能的效率高，能量损失小。
非线性效应
总结词
压电陶瓷在极化处理后具有显著的压电效应和非线性效应。
详细描述
在极化处理后，压电陶瓷的压电常数会随施加电压的增加而增大，表现出非线性效应。这种非线性效应使得压电陶瓷在某些应用中具有更高的性能表现。
详细描述
压电陶瓷的压电常数、介电常数等性能参数随温度变化较小，具有良好的温度稳定性，使其在温度变化的环境中仍能保持稳定的压电性能。
机械品质因数
总结词
机械品质因数反映了压电陶瓷的机械能与介电能之比，是评价其能量转换效率的重要参数。
详细描述
高品质的压电陶瓷具有较高的机械品质因数，意味着其机械能转换为介电能的效率高，能量损失小。
压电方程
压电方程定义
压电方程是描述压电陶瓷在机械力和电场作用下的关系，是描述压电效应的数学模型。
常用的压电方程
常用的压电方程包括d33E、g33E等，其中d33E表示在3方向上施加单位力时，材料产生的电荷量与施加的电压之间的关系。

压电陶瓷

在电场E3和应力X1作用下，压电陶瓷片产生电位移

当E3 0，X1 ＝ 0, 产生的介电电位移：
D 3(1) = X33 E3 当E3 ＝ 0，X1 0, 产生的压电电位移： D 3(2) = d31 X1 当E3 0，X1 0, 产生的总电位移：
D3 ＝ D 3(1) ＋ D 3(2) = X33 E3 ＋ d31 X1

热力学关系（守恒定律）赋予物理性质本身的固有对称性对宏观物理性质的影响－－要求描述晶体宏观物理性质的二阶以上张量都是对称张量，如
介电常数张量元 ij = ji 应变 xij = xji
压电常数 dijk = dikj
压电陶瓷的介电常数

对各向同性介质， ij 为标量
对各向异性介质， ij 为二阶张量
X Di ij E j d i X E x d j E j s X
x Di ij E j ei x E X e j E j c x

第二类压电方程组
Ei ijX D j g i X

第三类压电方程组
D x g j D j s X
压电方程组
D3 ＝ X33 E3 ＋ d31 X1 x1 ＝ s11E X1＋ d31 E3
压电方程组

对于一般情况：
Di = ijX Ej + di µX µ
x = dj Ej + s µEX µ

可简写为： D= d X + X E x = sE X + d E

第一类压电方程组
类型第一类边界条件机械自由机械夹持机械自由机械夹持名称电学短路电学短路电学开路电学开路特点 dX=0 d x=0 dX=0 dx=0 dx0 dE=0 dX 0 dE=0 dx 0 dD=0 dX 0 dD=0

第22讲7-3铁电体物理效应

对于逆压电效应，其应变 x与电场强度 E （V/m）的关系为： x = d E
6
压电效应与压电常数
对于正和逆压电效应，压电常数d在数值上是相同的，
D x d X E
D, E
为矢量，
为张量 x, X
7
标量、矢量和张量
标量：与方向无关，如密度、质量、温度等；矢量：既有大小又有方向，如力、速度、电场强度等；张量：简单的说，张量概念是矢量概念和矩阵概念的推广，标量是零阶张量，矢量是一阶张量，矩阵（方阵）是二阶张量，而三阶张量则好比立体矩阵，更高阶的张量用图形无法表达。
和媒质的介电常数和导磁率
（2）色散现象
晶体的折射率与光的频率(波长)有关，这就是色散现象由于电子的质量比原子核的质量小得多，因此，可以近似地把原于核看成是固定不动的。此外，又由于电子运动的速度比光速小得多，所以电磁波对原子的主要作用表现为电磁波的电场E 对原子中电子的作用。
32
色散现象
一. 压电效应对于不存在对称中心的晶体，加在晶体上的外力除了使晶体发生形变以外，同时，还将改变晶体的极化状态，在晶体内部建立电场，这种由于机械力的作用而使介质发生极化的现象称为正压电效应。反之，如果把外电场加在这种晶体上，改变其极化状态，晶体的形状也将发生变化，这就是逆压电效应。二者统称为压电效应。
晶体的热释电效应实际上是一种热-电耦合效应，进一步分析热释电效应可以像压电效应一样列出晶体的热释电方程：
T Di ij E j pi T
S pi Ei C E T T

p i 为热释电常数
24
热释电效应与弹性边界条件
如果晶体是在机械夹持状态下加热的，即晶体的体积和外形被强制地保持不变，这时所观察到的热释电效应为第一类热释电效应如果晶体在机械自由状态下加热，那么晶体将因受热膨胀而产生应变，这种应变将通过压电效应产生电位移而叠加在第一类效应上，这种由于热膨胀通过压电效应耦合而产生的附加热释电效应称为第二类热释电效应自由晶体受热时的热释电效应是第一类效应和第二类效应之和 25

压电材料的基本方程

压电材料的基本方程一、引言压电材料是一种特殊的物质，具有压电效应。

其特点是在外力作用下会出现电荷分布的不均匀现象。

因此，压电材料广泛应用于传感器、振动器、滤波器等领域。

二、压电效应压电效应是指在某些晶体和陶瓷中，在外力作用下会产生电荷分布不均匀的现象。

这种不均匀分布的电荷可以被测量和利用。

三、基本方程1. 应变方程压电材料受到外力作用时，会发生形变，这种形变称为应变。

应变可以表示为：ε = ΔL/L其中，ΔL 是长度的改变量，L 是原始长度。

2. 电荷方程当一个压电材料受到外力作用时，会产生一个极化向量 P。

极化向量 P 与表面上的正常向量成正比例关系。

因此可以表示为：P = d * F其中，d 是比例系数（即压电系数），F 是外力。

3. 介质常数方程介质常数是指介质在储存能量时所需要的能量密度与相对介电常数之比。

对于一个压电材料，其介质常数可以表示为：C = ε / E其中，ε 是介电常数，E 是能量密度。

4. 能量密度方程当一个压电材料被压缩时，会储存能量。

这种储存的能量可以表示为：U = 1/2 * C * E^2其中，C 是介质常数，E 是电场强度。

四、应用压电材料的基本方程可以用于设计和制造各种传感器、振动器、滤波器等产品。

例如，在传感器中，通过测量压电材料产生的电荷来检测外力；在振动器中，通过施加交变电场来使压电材料振动；在滤波器中，则利用压电效应来过滤特定频率的信号。

五、结论总之，压电材料是一种特殊的物质，在外力作用下会发生形变和产生不均匀分布的电荷。

这种现象可以利用基本方程进行计算和设计各种产品。

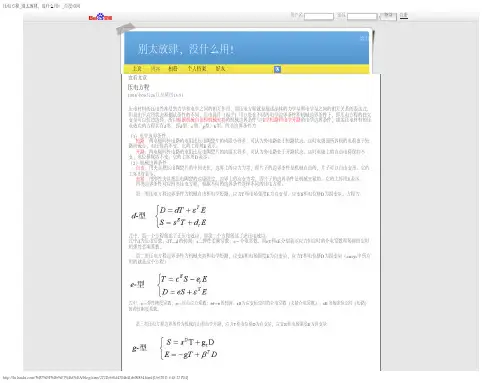
压电方程解析

应变常数；gT—g 的转置。βT为恒应力作用下的介质的隔离率。sD为恒电位移（开路）时弹性柔顺系数。第四类压电方程边界条件为机械夹持和电学开路，应变S和电位移D为自变量，应力T和电场强度E为因变量：
式中，h—压电应力常数；ht—h 的转置。βS为恒应变下（夹紧）的介质隔离率；cD为恒电位移（开路）时弹性刚度系数。理解并掌握了压电理论的基础知识、熟悉压电陶瓷的极化和压电方程等对于全面理解压电换能器的工作原理提供了相关的贴吧 | 浏览(930) | 评论 (0)
上一篇：《不要一辈子靠技术生存》下一篇：VM175
相关文章：
? 金属方程测人生 ? CCTV2 华尔街解说词第5集硅谷... 一元三次方程 ? ? proe方程曲线 Matlab 解方程 ? ? 用Excel解方程(组) 规划求解 MATLAB--二分法求解方程程序(完... ? 扩展欧几里德算法线性同余方程 ... ? ? Matlab非线性方程求根 ? 编程练习(不定方程)
式中，c—弹性刚度常数；e—压电应力系数；et—e 的转置。εS为应变恒定时的介电常数（夹紧介电常数），cE为场强恒定时（短路）的弹性刚度系数。
第三类压电方程边界条件为机械自由和电学开路，应力T和电位移D为自变量，应变S和电场强度E为因变量：
/%B7%BF%B6%F7%BA%EA/blog/item/2721b560d4704b41ebf8f834.html[1/6/2011 6:45:27 PM]
式中，第一个方程叙述了正压电效应，而第二个方程叙述了逆压电效应。式中d为压电常数，dT—d 的转置；s—弹性柔顺常数；ε— 介电常数。而εT和sE分别表示应力恒定时的介电常数和场强恒定时的弹性柔顺系数。第二类压电方程边界条件为机械夹持和电学短路，应变S和电场强度E为自变量，应力T和电位移D为因变量（ansys中所应用的就是这个方程）：B7%BF%B6%F7%BA%EA/blog/item/2721b560d4704b41ebf8f834.html[1/6/2011 6:45:27 PM]t

4.1 压电方程

D Tij cijkl Skl hkij Dk , S Ei hikl Skl ik Dk .
第四类压电方程可以通过选内能U为热力学函数推导得到，式中，hkij 为压电刚度系数，cDijkl为开路弹性刚度系数，βSik为夹持介电隔离率。
16
旋转坐标系中的压电方程组
前面介绍的压电方程组是在主轴坐标系中的压电方程组,介电常数,弹性常数和压电常数都是在主轴坐标系中的数值。这些数值可以在相关手册中查到。但是实用的压电晶片所处的坐标系（一般以晶片的长、宽、厚为坐标轴）与主轴坐标系不同。
Q ni Di ds.
s
& n D &ds. I Q i i
s
I
V . ZL
V 1 2
7
典型力学边界条件：自由与刚性夹持典型电学边界条件：短路与开路
类别名称特点可测常数
第一类边界条件
机械自由和电学短路
T 0, C; S 0, C; E 0, C; D 0, C.
物理意义：压电应变常数等于在恒电场下(电学短路)，由应力分量的单位变化引起电位移分量的变化量；或者等于在恒应力下(机械自由)，由电场强度分量的单位变化引起应变分量的变化量。短路弹性柔顺常数居于恒电场下由应力分量的单位变化引起应变分量的变化量。自由介电常数等于恒应力下，由电场强度分量的单位变化引起电位移分量的变化量。 12
S 0, C; T 0, C; E 0, C; D 0, C. T 0, C; S 0, C; D 0, C; E 0, C.
S 0, C; T 0, C; D 0, C; E 0, C.
T E E ij , sij , cij

12.02 二、压电常数及压电常数矩阵

z (3)y (2)o压电效应的表达式ij Q d F =压电元件受到沿一定方向的外力F 作用时，在相应的表面产生表面电荷Q：ij q d σ=F 1(σxx )F 3(σzz )F 2(σyy )F 4(τyz )F 5 (τzx )F 6(τxy )石英晶体切片的力-电分布q σ—应力(N/m 2)。

压电常数(C/N)（piezoelectric constant）z (3)y (2)oF 1(σxx )F 3(σzz )F 2(σyy )F 4(τyz )F 5 (τzx )F 6(τxy )压电常数d ij 两个下角注的含义¾i －晶体极化方向—正压电效应j ＝1、2、3、4、5、6，分别表示沿x 、y 、z 轴方向作用的单向应力和在垂直于x 、y 、z 轴的平面内作用的剪切力。

¾j －受力的性质i =1、2、3,分别表示产生电荷的表面垂直于x 、y 、z 轴。

¾i －所加电场的方向—逆压电效应¾j －产生应变的方向i =1、2、3,分别表示施加的电场方向沿x 、y 、z 轴。

j ＝1、2、3、4、5、6，分别表示沿在x 、y 、z 轴方向产生的单向应变和在垂直于x 、y 、z 轴的平面内产生的剪切应变。

压电常数d ij 两个下角注的含义z (3)y (2)oF 1(σxx )F 3(σzz )F 2(σyy )F 4(τyz )F 5 (τzx )F 6(τxy )举例在沿着Y 方向施加力的时候，在X 方向产生电场。

（正）在沿着X 方向施加电场的时候，在Y 方向产生应变。

（逆）在垂直于Y轴的平面施加剪切力的时候，在Y方向产生电场。

（正）在沿着Y方向施加电场的时候，在垂直于Y 轴的平面产生剪切应变。

（逆）有缘学习更多＋谓ｙｇｄ３０７６或关注桃报：奉献教育（店铺）压电常数矩阵晶体在任意受力状态下所产生的表面电荷密度：－在垂直于x 轴、y 轴和z 轴的表面上产生的电荷密度；zz yy xx q q q ,,xy zx yz zz yy xx yy d z d d d d d q ττσσσ262524232221+++++=xy zx yz zz yy xx zz d d d d d d q τττσσσ363534333231+++++=xx xx d q σ11=yy d σ12+zz d σ13+yz d τ14+zx d τ15+xy d τ16+zz yy xx σσσ,,－沿x 轴，y 轴和z 轴方向作用的拉或压应力；xy zx yz τττ,,－在yz 平面、zx 平面和xy 平面内作用的剪应力。

压电材料及及其本构方程

D3 31 32 33E3
用张量形式表示：
Di ij E j
(i, j 1,2,3) (4)
上式中εij称为介电常数，第一个下标表示电场位移方向；第二个下标表示电场强度分量的方向。对于已经极化的压电材料εij只有ε11= ε22和ε33
在上述情况下，也可以采用电应变εi和电场强度E来描述它的电行为。
性刚度常数，分别为短路弹性刚度系数 CiEj
和开路弹性刚度系数 CiDj ，其单位为N/m2；而使应力改变一个单位所引起的应变变化量称为弹性柔度常数, 对于压电材料它同样也有两个弹性柔
度常数，分别为短路弹性柔度系数 siEj
和开路弹性柔度系数 siDj ，其中上标E表示在常电场
或零电场情况下所得到的参数，而上标 D表示为在常电位移或零电位移情况下所得到的参数。根据以上定义有：
补充：压电效应的历史
1917年，Paul Langevin第一个应用了压电效应：超音波水下探测器，用来探测潜艇，这个潜艇探测器，主要是将一很薄的石英晶体包覆于两片铁板内并粘结成一体，使其通电后能发出高频声音，再接收打到物体表面后回传信号，以来回时间判断其距离及位置。
Pierre Curie (1பைடு நூலகம்59-1906), Nobel Prize in Physics, 1903
标轴表示法对应如下：
1 1
2
2
3 4
233
5
31
6 12
1 1
2
2
3 4
233
(10)
5
3
1
6 12
(3) 压电材料的压电方程(力电耦合行为)
由压电材料的电行为和力行为叠加即可得到压电材料的压电方程：

压电方程

压电材料的压电性涉及到力学和电学之间的相互作用，而压电方程就是描述晶体的力学量和电学量之间的相互关系的表达式。

但是由于应用状态和测试条件的不同，压电晶片（振子）可以处在不同的电学边界条件和机械边界条件下，即压电方程的独立变量可以任意选择，所以根据机械自由和机械夹持的机械边界条件与电学短路和电学开路的电学边界条件，描述压电材料的压电效应的方程共有4类，即d型、e型、g型、h型。

四类边界条件为：（1）电学边界条件短路：两电极间外电路的电阻比压电陶瓷片的内阻小得多，可认为外电路处于短路状态。

这时电极面所累积的电荷由于短路而流走，电压保持不变。

它的上标用E表示。

开路：两电极间外电路的电阻比压电陶瓷片的内阻大得多，可认为外电路处于开路状态。

这时电极上的自由电荷保持不变，电位移保持不变。

它的上标用D表示。

（2）机械边界条件自由：用夹具把压电陶瓷片的中间夹住，边界上的应力为零，即片子的边界条件是机械自由的，片子可以自由变形。

它的上标用T表示。

夹紧：用刚性夹具把压电陶瓷的边缘固定，边界上的应变为零，即片子的边界条件是机械夹紧的。

它的上标用S表示。

四类边界条件对应四类压电方程，根据不同的边界条件选择不同的压电方程。

第一类压电方程边界条件为机械自由和电学短路，应力T和电场强度E为自变量，应变S和电位移D为因变量。

方程为：式中，第一个方程叙述了正压电效应，而第二个方程叙述了逆压电效应。

式中d为压电常数，dT—d的转置；s—弹性柔顺常数；ε—介电常数。

而εT和sE分别表示应力恒定时的介电常数和场强恒定时的弹性柔顺系数。

第二类压电方程边界条件为机械夹持和电学短路，应变S和电场强度E为自变量，应力T和电位移D为因变量（ansys中所应用的就是这个方程）：式中，c—弹性刚度常数；e—压电应力系数；et—e的转置。

εS为应变恒定时的介电常数（夹紧介电常数），cE为场强恒定时（短路）的弹性刚度系数。

第三类压电方程边界条件为机械自由和电学开路，应力T和电位移D为自变量，应变S和电场强度E为因变量：式中，β—自由倒介电常数；g—压电应变常数；gT—g的转置。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

P3 E0 0 （4-8）

22
根据（4-6）、（4-7）以及（4-8）式的结果，
可得到石英晶体的正向压电效应表示式用矩阵表
示为：
X1
P1 d11

P2

0
P3 0
d11 0 0
0 0 0
d14 0 0
0 d14

2
压电效应的基本现象
通俗来说:压电效应是指材料在压力作用下产生电信号的效应;或者在电场作用下,材料发生机械形变的现象。压电效应有严格的定义，上述说法只是一个简单直观描述。压电效应由压电方程描写；材料的压电性由压电常数决定。

3
压电效应的基本现象

x
2

d
1
2

x3 x4

d 13 d 14

x x
5 6

d d
15 16
d 22 d 23 d 24 d 25 d 26
0 0 0 0

E E E
1 2 3

0

35
从上式可以看出：
（1）对于石英晶体不是在任何方向上都存在逆压电效应，只有在某些方向，在某些电场作用下，才能产生逆压电效应。例如，当x方向电场分量E1 作用时，可产生压电形变x1和x2以及压电切应变 x4。又如当z方向电场分量E3作用时，晶体不会产生任何形变。
P 2 E 0 ( d 2 5 X 5 d 2 6 X 6 ) ( d 1 4 X 5 2 d 1 1 X 6 )
（4-7）即石英晶体的压电常数d25=-d14，d26=-2d11。

21
当选z方向为电极面，重复上述实验，当电场 E=0时，应力张量X对z方向的极化强度分量P3 的贡献为：
0
0 2d11
0

X2 X3 X4 X5 X6

23
在压电物理中常用电位移D代替极化强度P，当电场E=0时，D=0E+P=P，电位移的三个分量： D1=P1，D2=P2，D3=P3。将这些关系代入到（4-9）式，即得到用电位移分量与应力分量表示的石英晶体正向压电效应
d11 d12 d13 d14 d15 d16 dd21 d22 d23 d24 d25 d26
d31 d32 d33 d34 d35 d36

28
可见压电常数d的矩阵形式是一个三行六列矩阵，
即d是一个三级张量。一般情况下正压电效应的
表示式为：
X1
其中下标X表示应力张量X=0。

32
（2）以y面为电极面，当晶片只受到y方向的电场分量E2作用时，分别产生切应变x5和x6，这些应变都与E2正比，即：
x5 X d25E2 d14E2 x6 X d26E2 2d11E1

33
（3）以z面为电极面，当晶片只受到z方向的电场分量E3作用时，晶片不产生任何形变。

25
从以上两式式可以看出：
（1）对于石英晶体不是在任何方向上都存在压电效应，只有在某些方向上，在某些力的作用下，产生才能出现正压电效应。例如，在石英晶体x 方向，只有X1、X2、X4作用时，才能在x方向压电效应，而X3、X5、X6不能在x方向压电效应。在石英晶体的z方向，不论在什么方向作用多大的力，都不能在z方向压电效应。
D1 d11

D2

d21
D3 E d31
d12 d22 d32
d13 d23 d33
d14 d24 d34
d15 d25 d35
d16 d26 d36

X2 X3 X4 X5 X6

的表示式为，

24
D1 d11 d11 0 d14 0

D2

0
0 0 0 d14
D3 E 0 0 0 0 0
式中附标E表示电场强度E=0。
X1
0 2d11
0

X2 X3 X4 X5 X6

19
综合上述实验结果得到，选x方向为电极面，当电场E=0时，应力张量X对x方向的极化强度分量P1的贡献为：
P 1E 0 (d 1 1 X 1 d 1 1 X 2 d 1 4 X 4 )

20
当选y方向为电极面，重复上述实验，当电场E=0 时，应力张量X对y方向的极化强度分量P2的贡献为：

12
（Fy/lwlt）为y方向的应力X2，于是有
P(2) 1

X2
即：
P(2) 1
d12X2
式中，P(2)1为晶片只受到y方向的应力X1作用时，在x方向产生的极化强度分量，比例系数 d12也称为压电常数。

13
实验上还发现当X1=X2时，存在P(2)1= -P(1)1，由此可得d11=-d12，即石英晶体的压电常数d12 的大小等于压电常数d11的负值。
压电效应与压电方程
Piezoelectric effect Piezoelectric equations

1
主要内容
压电效应的基本现象石英晶体的压电效应，压电方程组压电常数与对称性压电晶体的切割, 四类压电方程组，旋转坐标系，次级压电效应，压电常数之间的关系机电耦合系数

6
图4-1：—石英晶体属于六角晶系32点群，它的坐标系o-xyz。

7
光轴电轴机械轴
z轴与天然石英晶体的上、下顶角连线重合（即与晶体的C轴重合）。因为光线沿z轴通过石英晶体时不产生双折射，故称z轴为石英晶体的光轴。
x轴与石英晶体横截面上的对角线重合（即与晶体的a轴重合），因为沿x方向对晶体施加压力时，产生的压电效应最显著，故常称x轴为石英晶体的电轴。

10
因为（ q(1)1/llw ）是极化强度分量 P(1)1 ；（Fx/llw）为x方向的应力X1，于是得到
P(1) 1

X1
即：
P(1) 1
d11X1
(4-1)
式中，P(1)1为晶片只受到x方向的应力X1作用时，在x方向产生的极化强度分量，比例系数d11称为压电常数。
晶体的介电常数、弹性常数与晶体的对称性密切相关。同样，压电常数也与晶体的对称性密切相关。因此不是从压电晶体上随意切下一块晶片，就能做压电元件，而是要根据该压电晶体的压电常数来设计晶片的切割。

4
正压电效应
当压电晶体受到外力而发生形变时，在它的某些表面上出现与外力成线性比例电荷积累，这个现象称为压电效应。是一种线性响应！

36
（2）逆压电常数与正压电常数相同，并且一一对应。
（3）有正压电效应方向就有相应的逆压电效应。晶体中那个方向上有正压电效应，则此方
向上一定存在逆压电效应。

37
对于一般的情况，例如三斜晶系中的压电晶体，它的逆压电效应用矩阵表示即为，
x1 d11 d 21 d 31

11
（2）当晶片受到沿y方向的力Fy作用时，通过冲击电流计，可测出在x轴方向电极面上的电荷 q(2)1 ，并发现 x 方向电极面上的电荷密度（q(2)1/llw）的大小与y方向单位面积上的力（Fx/lwlt）成正比，因为（q(2)1/llw）是极化强度分量P(2)1。

14

15
（3）当晶片受到沿z方向的力Fz作用时，通过冲击电流计，并发现x方向电极面上不产生电荷。即有
P(3) 1
d13X3
0
(4-3)
因为X30，故压电常数d13=0。由此可见，对于 x切割的石英晶片，当z方向受到应力X3的作用时，在x方向并不产生压电效应。
29
或简写为：
D dX E
或：
6
D mE dm jX j; m 1 ,2 ,3 ; j1 ,2 ,3 ,4 ,5 ,6 j 1

30
逆压电效应 inverse effect
当晶体受到电场E的作用时，晶体产生与电场成线性比例的畸变，这个现象称为逆压电效应。逆压电效应的产生是由于压电晶体受到电场的作用时，在晶体内部产生应力，这个应力常称为压电应力。通过压电应力的作用，产生压电形变。仍以石英晶体为例说明如下。

31
（1）选用石英晶体的x切割晶片，以x面为电极面。当晶片只受到x方向的电场分量E1作用（应力张量 X=0）时，分别在x方向和y方向产生应变x1和x2 以及切应变x4，这些应变都与E1成正比，即
x1 X d11E1 x2 X d12E1 d11E1 x4 X d14E1

26
（2）石英晶体的独立压电常数只有d11与d14 两个，它们的数值是：
d11=-2.3110-12库仑/牛顿， d14= 0.7310-12库仑/牛顿。

27
对于一般的情况，例如属于三斜晶系1（C1）点群的压电晶体是完全各向异性的，独立的压电常数共有18个，用矩阵表示即为，

16
（4）当晶片受到切应力X4作用时，通过冲击电流计，可测出在x方向电极面上的面电荷密度（q(4)1/llw）= P(4)1，并发现P(4)1与X2 成正，于是
P(4) 1
d14X4
(4-4)
式中， P(4)1为晶片只受切应力X4作用时，在x 方向产生的极化强度分量，比例系数d14称为压电常数。