下载文档原格式
我国居民消费价格指数预测研究--基于LASSO-IPSO-LSTM
组合预测模型
薛洁;冯楠
【期刊名称】《统计科学与实践》
【年(卷),期】2022()7
【摘要】针对CPI时序数据的非线性特征以及传统的统计预测方法、神经网络的不足,文章提出LASSO-IPSO-LSTM组合预测模型。
以2011年1月至2020年12月我国CPI月度数据为研究对象,运用LASSO方法筛选出对CPI产生显著影响的指标,利用改进PSO算法优化LSTM网络的超参数,进而构建组合模型对CPI数据进行预测。
结果表明,LASSO-IPSO-LSTM组合预测模型的预测误差均小于其他模型,且平均绝对百分比误差仅为0.53%,说明该模型具有良好的泛化能力,可为准确预测CPI提供一种稳定而有效的方法。
【总页数】5页(P15-19)
【作者】薛洁;冯楠
【作者单位】杭州电子科技大学
【正文语种】中文
【中图分类】F72
【相关文献】
1.基于GM(1,1)理论的中国居民消费价格指数预测模型研究
2.基于遗传算法的我国居民消费价格指数短期灰色预测研究
3.基于小波分析的SVM和ARMA预测模型
的实证研究——以居民消费价格指数CPI为例4.基于半参数时间序列模型的我国城市居民消费价格指数的预测研究5.基于新维无偏灰色RBF神经网络的居民消费价格指数预测模型
因版权原因，仅展示原文概要，查看原文内容请购买。
居民消费价格指数时间序列模型分析内容摘要由于去年来我国居民消费价格指数（CPI）出现了持续较快上涨，而CPI对经济生活各个方面都有重要影响，因此本文选用时间序列模型来分析其变化规律，以期能够根据其规律对经济生活中某些决策起到某些借鉴作用。
本文首先描述性分析了我国CPI数据变动情况，然后用乘积季节模型来拟合该数据变动规律，并根据拟合模型作了短期预测。
从模型拟合效果和预测结果看，乘积季节模型能够较好地说明CPI数据变动规律。
关键词：居民消费价格指数（CPI）乘积季节模型预测相关图ABSTRACTBecause the CPI （Consumer Price Index） has been going up increasingly and sharply since last year and it' s very important for the people in all the aspects of the economy life, this text selects the time series model in order to draw up the regulations in the data of the CPI and make use of them in the decision-makings・ First of all, this text described fluctuations of the CPI in China, fitted the regulations with the multiplicative seasonal model and forecasted the short-term CPI with the mode1・ Compared with the estimation and the forecast in the model, the multiplicative seasonal model made a good descriptionof the regulations and trends about the data・KEY WORDS： Consumer Price Index Multiplicative Seasonal ModelsForecastCorrelation Function Charts---------------------------------------------- 1页一、居民消费价格指数概念和经济意义 ------------------------------------ 1页二、数据结构检验及初步分析 -------------------------------------------- 2页三、季节调整模型历史和建模思想 ---------------------------------------- 3页四、我国CPI数据建模和预测-------------------------------------------- 4页（一）、数据平稳化检验（二）---------------------------------------------------------------- 、数据平稳化过程--------------------------------------------------------------- 5页（三）------------------------------------------------------------------- 、建立乘积季节模型------------------------------------------------------------ 7页（四）------------------------------------------------------------------- 、预测和分析------------------------------------------------------------------ 8页结语--------------------------------------------------------------------------------------------------- 9页（一）-------------------------------------------------- 预测合理性和可行性9页（二）-------------------------------------------------------- CPI预测意义9页（三）------------------------------------------------------ 预测中存在问题9页参考文献10页居民消费价格指数时间序列模型分析居民消费价格指数不仅是反映通货膨胀首要指标，也是及居民生活水平密切相关重要指数，该指数被用来监控和预警宏观经济运行状态，并作为重要依据来调整我国财政政策和货币政策。
对居民消费价格指数进行准确地预测，是合理制定宏观经济政策的前提。
本文选取武汉市２００３年１月至２００９年１１月居民消费价格指数的月度定基比数据，采用时间序列分解法建立模型并进行预测。
从居民消费价格指数中分解出季节因素和长期趋势因素，并对居民消费价格指数的变化做出准确的预测，以期为宏观经济分析和决策提供参考。
一、武汉市居民消费价格指数时间序列分析时间序列分解模型的基本思想是序列的各种变化受到长期趋势、周期性循环要素、季节性变化和不规则变动这四个因素的影响。
其中（１）长期趋势因素（Ｔ）：反映经济现象在一个较长时间内的发展方向，它可以在一个相当长的时间内表现为一种近似直线的持续向上或持续向下或平稳的趋势。
（２）周期性循环要素（Ｃ）：是一种周期性变动，它是受各种经济因素影响的上下起伏不定的波动。
（３）季节性要素（Ｓ）：是受季节变动影响所形成的一种长度和幅度固定的周期性波动。
（４）不规则要素（Ｉ）：是受各种偶然因素影响所形成的不规则变动。
时间序列可以表示为上述四个因素的函数。
时间序列分解模型有很多，最常用的有加法模型：时间序列Ｙ等于以上四个因素之和；乘法模型：时间序列Ｙ等于以上四个因素的乘积；混合模型：时间序列Ｙ等于长期趋势与季节性要素的乘积再加上循环要素与不规则要素之和。
本文选取武汉市２００３年１月至２００９年１１月居民消费价格指数的月度定基比数据Ｙ，由于是定基比数据，因此在各期之间具有可比性。
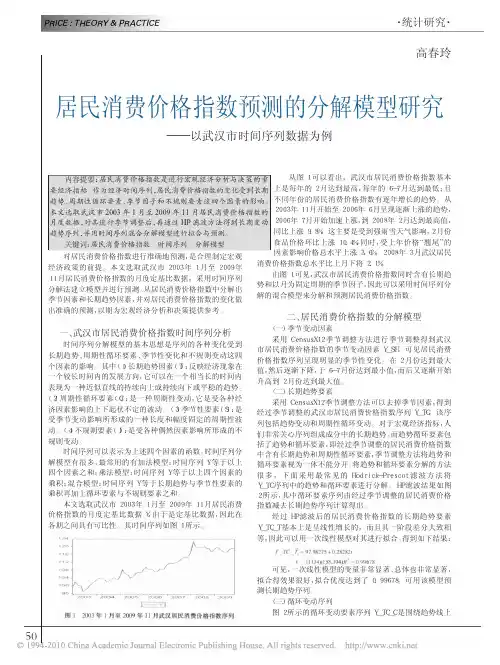
其时间序列如图１所示。
从图１可以看出，武汉市居民消费价格指数基本上是每年的２月达到最高，每年的６－７月达到最低；且不同年份的居民消费价格指数有逐年增长的趋势。
从２００３年１１月开始至２００６年６月呈现逐渐上涨的趋势，２００６年７月开始加速上涨，到２００８年２月达到最高值，同比上涨９．８％，这主要是受到强雨雪天气影响，２月份食品价格环比上涨１０．４％，同时，受上年价格“翘尾”的因素影响价格总水平上涨３．６％。
２００８年３月武汉居民消费价格指数总水平比上月下将２．１％。
居民消费价格指数的时间序列分析作者：杨志来源：《经济研究导刊》2013年第35期摘要：社会经济现象往往受许多因素的影响，且这些因素之间又保持着错综复杂的联系，因而，运用结构式的因果模型进行分析和预测往往比较困难，而根据其自身的变动规律建立动态模型即时间序列分析则是一种行之有效的方法。
对此，介绍了平稳时间序列分析的思想及方法，并以1995—2006年全国居民消费价格指数统计资料为依据，建立其时间序列模型。
关键词：时间序列；居民消费价格指数；模型中图分类号：F126；C913 文献标志码：A 文章编号：1673-291X（2013）35-0008-03一、平稳时间序列模型介绍（一）ARMA模型模型（3）的无条件均值、无条件方差和条件方差都是常数。
条件均值随着时间的变化而变化。
所以，可以利用该模型对未来进行预测，应该可以得到比平均数更好的预测，因为该预测会随着新数据的增加而不断调整。
假设我们得到的时间序列是平稳的，就可以对它建立ARMA模型。
（二）ARIMA模型上述的ARMA模型是平稳时间序列模型。
现实中很多时间序列都存在一定的趋势，因此是非平稳的。
对于非平稳时间序列不能直接建立ARMA模型，我们可以通过对非平稳序列进行差分以得到平稳序列。
若某时间序列是非平稳的，通过差分运算，得到平稳性的序列称为单整序列。
如果序列Xt通过d次差分成为一个平稳序列，而这个序列差分d-1时却不平稳，那么则称序列Xt为d 阶单整序列，记为Xt～I（d）；特别地，如果序列Xt本身是平稳的，则称为零阶单整序列，记为Xt～I（0）。
对于非平稳时间序列Xt，经过d阶差分变换得到平稳序列ΔdXt，可对其建立ARMA（p，q）模型，即称上述模型为求和自回归滑动平均模型，记为ARIMA（p，d，q），其中，p，d，q分别表示自回归阶数、差分阶数、移动平均阶数，当d=0时，ARIMA（p，d，q）模型就是ARMA 模型。
（三） ARMA模型的建模步骤ARMA（p，q）模型的建模步骤如下：首先，对原时间序列进行平稳性检验，如果序列不满足平稳性条件，可以通过差分变换或者对数差分等其他变换，使原时间序列满足平稳性条件。
我国居民的消费水平时间序列分析及预测作者：刘敏来源：《商场现代化》2014年第21期摘要：本文采用时间序列分析及预测的方法对我国居民的消费水平的发展趋势进行分析预测。
通过EViews7.0建立时间序列模型，选择合适模型进行拟合，并作出预测。
利用二次型模型和指数型模型，用最小二乘法进行参数估计。
利用拟合优度大小和拟合图相结合，选出最优模型及预测值。
关键词：消费水平；时间序列；二次型模型；指数型模型一、引言居民消费水平是指居民在物质产品和劳务的消费过程中，对满足人们生存、发展和享受需要方面所达到的程度。
通过消费的物质产品和劳务的数量和质量反映出来。
现在物价上涨，我国的消费水平和消费能力提高，对我国的经济发展有一定的推动作用。
所谓时间序列是按照时间的顺序排列的统计数据。
对时间序列进行观察，研究，找出一定的规律，预测将来的趋势。
在日常生活，生产中，时间序列随处可见，时间序列分析的应用领域很广泛。
本文将运用于经济领域。
二、样本与数据处理本文选用1993年-2012年的居民的消费水平年度数据作为样本。
（数据来源：中国统计年鉴2012）根据EViews7.0得到时序图，知样本总体呈现出不断上升的趋势。
进一步做单位根检验可得：P值为1，P值大于0.05，故不能拒绝原假设，即存在单位根，该序列不平稳。
由于序列不平稳，所以对样本数据进行差分处理。
经过一阶差分后的单位根检验结果中，P值为0.4349，P值大于0.05，故接受原假设，即存在单位根，该序列不平稳。
经过二阶差分后的单位根检验结果中，P值为0.01，P值小于0.05，故拒绝原假设，即不存在单位根，该序列平稳。
三、模型的选择1. 二次型模型的建立由于原序列经过二阶差分得到平稳序列可知，此序列可能为二次型序列，所以对其进行二次型模型处理。
（1）确定二次型模型由EViews7.0图对原序列的二次型拟合图由图1可得到二次型模型，但也需要对其残差自相关等分析，而后对残差进行模型拟合。
我国居民消费价格指数时间序列模型与预测摘要: 居民消费价格指数CPI 是具有重要经济意义的指标，它的增长具有一定的内在规律性，而大多数经济时间序列存在惯性或者说是迟缓性，通过对这种惯性的分析可以由时间序列的当前值和过去值对未来值进行预测。
本文利用了ARMA 模型对我国1993年8月—2014年10月的月度CPI 的时间序列数据进行建模分析，并利用所建立的模型对我国的居民消费价格指数进行了短期预测。
关键词: CPI ARMA 模型 时间序列 预测时间序列预测是通过对预测目标自身时间序列的处理来研究其变化趋势的。
即通过时间序列的历史数据揭示现象随时间变化的规律，将这种规律延伸到未来从而对该现象的未来作出预测。
文中所用的ARMA 模型是目前最常用的随机时间序列拟合模型。
其基本思想是:某些时间序列是依赖于时间t 的一组随机变量，构成该时序的单个序列值虽然具有不确定性。
但整个序列的变化却有一定的规律性，可以用相应的数学模型近似描述。
通过对该数学模型的分析研究，能够更本质地认识时间序列的结构与特征达到最小方差意义下的最优预测。
研究我国的居民消费价格指数CPI 的统计规律性和变动趋势，对于我国相关的经济发展政策有特别重要的意义。
本文利用我国1993年8月—2014年10月的月度CPI 历史数据为样本，利用在研究一个国家或地区经济和商业预测中比较先进适用的时间序列模型之一的ARMA 模型对样本进行统计分析，以揭示我国居民消费价格指数CPI 变化的内在规律性，并进行后期预测。
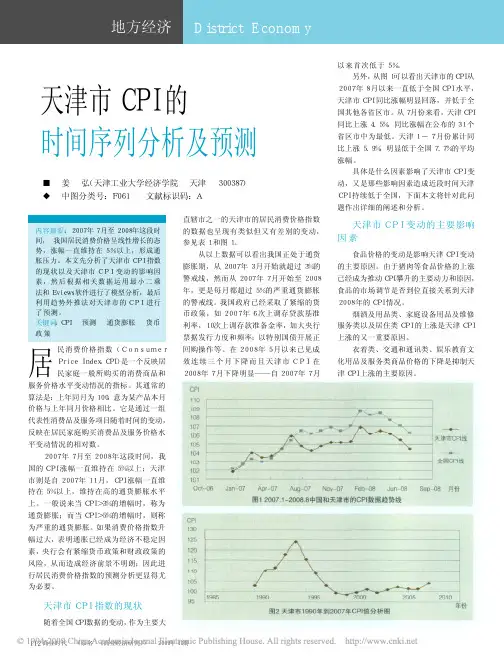
一、数据预处理1.平稳性检验 （1）时序图96100104108112116120124128255075100125150175200225250居民消费价格指数(上年同月=100)从上图可知，该数据有截距项，无明显变动趋势。
（2）ADF 单位根检验Null Hypothesis: CPI has a unit rootExogenous: ConstantLag Length: 12 (Automatic - based on SIC, maxlag=15)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -4.798075 0.0001 Test critical values: 1% level -3.4572865% level -2.87328910% level -2.573106*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(CPI)Method: Least SquaresDate: 11/26/14 Time: 22:25Sample (adjusted): 14 255Included observations: 242 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.CPI(-1) -0.032085 0.006687 -4.798075 0.0000 D(CPI(-1)) 0.168383 0.053134 3.169021 0.0017 D(CPI(-2)) 0.075710 0.053347 1.419191 0.1572 D(CPI(-3)) 0.043381 0.053218 0.815167 0.4158 D(CPI(-4)) 0.106993 0.053157 2.012767 0.0453 D(CPI(-5)) 0.059208 0.052698 1.123534 0.2624 D(CPI(-6)) 0.022702 0.052143 0.435374 0.6637 D(CPI(-7)) 0.077984 0.051391 1.517469 0.1305 D(CPI(-8)) 0.112575 0.051273 2.195607 0.0291 D(CPI(-9)) 0.028500 0.051586 0.552476 0.5812 D(CPI(-10)) -0.039258 0.051568 -0.761295 0.4473 D(CPI(-11)) 0.210599 0.051451 4.093188 0.0001 D(CPI(-12)) -0.481773 0.049770 -9.680053 0.0000C 3.261175 0.693266 4.704072 0.0000R-squared 0.474112 Mean dependent var -0.100000 Adjusted R-squared 0.444127 S.D. dependent var 0.690841 S.E. of regression 0.515070 Akaike info criterion 1.567081Sum squared resid 60.48765 Schwarz criterion 1.768920Log likelihood -175.6168 Hannan-Quinn criter. 1.648389F-statistic 15.81172 Durbin-Watson stat 2.004497Prob(F-statistic) 0.000000由检验结果可知，在5%的置信度水平下，p=0.0001<0.05, 通过单位根检验，数据平稳。
1994-2012年江苏省居民消费价格指数的时间序列分析班级：统计1班姓名：陈晶晶学号：09704122摘要居民消费价格指数（CPI）是宏观经济分析和决策，价格总水平监测和调控以及国民经济核算的重要指标。
本文利用1994-2012年江苏省居民消费价格指数的月度数据，运用Eviews 软件建立一个乘积季节模型，并用这个模型对江苏省未来的居民消费价格指数进行合理的预测。
关键词居民消费价格指数时间序列分析乘积季节模型预测分析一．引言居民消费价格指数(CPI)是用来测定一定时期内居民支付所消费商品和服务价格变化程度的相对数指标。
它既是反映通货膨胀程度的重要指标，也是国民经济核算中的缩减指标。
一般说来，当CPI>3% 的增幅时，我们称为通货膨胀；而当CPI>5% 的增幅时，我们把它称为严重的通货膨胀。
这一指标影响着政府制定货币、财政、消费、价格、工资、社会保障等政策，同时，也直接影响居民的生活水平及评价。
居民消费价格指数反映的市场价格信号真实．带动价格舆论导向正确，有利于改善价格总水平调控。
首先，它有利于维护正常的经济生活和市场价格信息秩序。
其次，有利于引导消费形成合理的消费价格，促进有效需求。
再次，它有利于综合运用价格和其他经济手段，实现价格总水平调控目标。
【1】所以，对该指标的分析与预测是非常有意义的工作。
本人在阅读与之有关的参考文献时，发现很多学者采用全国的CPI数据进行时间序列分析，就某个省份或某个城市的CPI数据研究很少，而且采用的模型也各不相同，所以本人就用江苏省1994-2012年的居民消费价格指数进行了时间序列分析。
二．数据描述和模型说明1.数据描述1994年1月——2012年3月江苏省居民消费价格指数如下表：（数据来源：/data/mac/jmxf_dq.php?symbol=320000）1月2月3月4月5月6月7月8月9月10月11月12月1994年123.9 125.9 122.6 121.4 119.8 120.6 122.3 123.4 125.5 125.6 124.9 121.61995年120.8 119.6 119.1 118.1 118.4 117.4 115.4 113.1 112.5 112.1 111.6 1121996年112.6 111.9 111.8 111.5 109.9 108.9 109.3 109.2 107.6 106.9 106.6 105.51997年104.2 104.3 103.1 103 102.4 101.8 101 100.8 100.9 100.1 99.7 99.41998年99.5 99.5 100.4 99.5 99.4 99 99 99.6 99.2 99.4 99.5 99.21999年98.9 98.8 98.1 97.6 97.9 98.7 99.3 98.9 98.9 99.3 99.2 99.32000年100.4 101.4 100.4 100.1 99.7 99.6 99.7 99.4 99.5 99.4 100.3 100.72001年101.6 100.4 101 101.9 102 101.4 101.4 101.2 100.3 100 99.4 99.32002年99.2 99.9 99.3 98.6 99 99.5 99.3 99.4 99.1 99 99.1 99.42003年100 100.2 100.6 100.7 100.1 99.6 100.3 101 101.2 102.2 103.2 103.22004年103.2 102.4 103.6 104.3 105.1 105.6 105.3 105.5 105.1 104.1 102.5 102.12005年102.2 104.4 103 102 101.5 101.4 101.8 101.3 101.4 102.1 102 102.32006年102.5 101.2 100.9 101.4 101.5 101.4 101.3 101.5 101.3 101 102 103.12007年102 102 102.5 102.7 103.1 104 105.2 106 105.9 106.2 106.5 105.62008年106.1 107.7 107.7 107.6 107.1 106.9 106 104.6 104.3 103.5 101.9 101.42009年101.4 99.5 99.6 98.9 98.8 98.3 98 98.8 99.3 99.6 100.6 102.12010年101.7 102.4 102.4 103.2 103.7 103.5 104.1 103.9 104.6 105.2 106.1 1052011年105.1 105.7 105.6 105.3 105.7 106.9 106.4 106 105.4 104.8 103.5 103.62012年103.9 102.9 103.5首先，做出序列时序图和自相关图，如下：X13012512011511010510095949698000204060810可以看出该序列是不平稳的序列，做1阶12步差分dx=d(x,1,12)得到如下时序图：DX4321-1-2-3-4949698000204060810可以看出差分后的序列是平稳序列。
居民消费价格指数分析及预测居民消费价格指数是反映一个地区经济生活状况的重要指标，研究分析某一地区的指数变化趋势有着重要的现实意义。
本文通过建立模型，对西安市近些年居民消费价格指数数据进行了分析。
实证分析的结果表明，3,1,3模型能够较好地拟合数据，预测的准确度比较高，可以为市场的短期预测与经济政策的制定提供一定的参考依据。
指数；模型；预测一、引言居民消费价格指数是用来衡量一个地区通货膨胀率的重要指标。
通俗的讲，就是该地区市场上一组有代表性的消费品及服务项目的价格水平在一段时间内增长的百分比。
一般认为在2~3属于可接受范围内，如果该指标高于3则认为该地区存在通货膨胀的风险。
[1]由于该指标的重要性，国内学者对于它的研究分析有很高的热度。
刘颖等用季节调整方法对我国时间序列进行分析。
[2]雷鹏飞运用季节性模型对我国序列进行了有效地分析。
[3]郭玉等运用6构建了模型对我国的进行分析和预测。
[4]我国地理幅员辽阔，每个地区经济社会状况有所差异，一个地区的居民消费价格指数更能代表这一地区的经济生活情况，对于该地区的老百姓更是密切相关。
因此，对一个地区指数的分析和预测，可以准确掌握该地区老百姓的生活状况和未来的经济发展形势，对各级政府开展工作具有重要的指导意义。
本文通过建立模型，对西安市近些年指数的月度数据进行了分析与预测，为经济政策的制定提供了一定的参考依据。
二、模型在对传统的时间序列研究分析中，模型是其中一个重要方法，它是由自回归模型模型与移动平均模型模型为基础混合构成的。
但是模型含有一个假设条件就是该时间序列是平稳的，然而对于大多数的经济和金融时间序列，受到趋势、季节等一些随机因素的影响，会呈现出非平稳的特点。
根据这一现象，在本文中使用由博克斯-詹金斯提出的通过将时间序列进行差分变换从而达到平稳的模型,[5]来对时间序列进行建模。
该模型的表达式如下其中，ω是经过阶差分后得到的变量，即；δ为自回归系数；ɛ为移动平均系数；为自回归项数；为移动平均项数。
居民消费价格指数的时间序列分析作者：杨志来源：《经济研究导刊》2013年第35期摘要：社会经济现象往往受许多因素的影响，且这些因素之间又保持着错综复杂的联系，因而，运用结构式的因果模型进行分析和预测往往比较困难，而根据其自身的变动规律建立动态模型即时间序列分析则是一种行之有效的方法。
对此，介绍了平稳时间序列分析的思想及方法，并以1995—2006年全国居民消费价格指数统计资料为依据，建立其时间序列模型。
关键词：时间序列；居民消费价格指数；模型中图分类号：F126；C913 文献标志码：A 文章编号：1673-291X（2013）35-0008-03一、平稳时间序列模型介绍（一）ARMA模型模型（3）的无条件均值、无条件方差和条件方差都是常数。
条件均值随着时间的变化而变化。
所以，可以利用该模型对未来进行预测，应该可以得到比平均数更好的预测，因为该预测会随着新数据的增加而不断调整。
假设我们得到的时间序列是平稳的，就可以对它建立ARMA模型。
（二）ARIMA模型上述的ARMA模型是平稳时间序列模型。
现实中很多时间序列都存在一定的趋势，因此是非平稳的。
对于非平稳时间序列不能直接建立ARMA模型，我们可以通过对非平稳序列进行差分以得到平稳序列。
若某时间序列是非平稳的，通过差分运算，得到平稳性的序列称为单整序列。
如果序列Xt通过d次差分成为一个平稳序列，而这个序列差分d-1时却不平稳，那么则称序列Xt为d 阶单整序列，记为Xt～I（d）；特别地，如果序列Xt本身是平稳的，则称为零阶单整序列，记为Xt～I（0）。
对于非平稳时间序列Xt，经过d阶差分变换得到平稳序列ΔdXt，可对其建立ARMA（p，q）模型，即称上述模型为求和自回归滑动平均模型，记为ARIMA（p，d，q），其中，p，d，q分别表示自回归阶数、差分阶数、移动平均阶数，当d=0时，ARIMA（p，d，q）模型就是ARMA 模型。
（三） ARMA模型的建模步骤ARMA（p，q）模型的建模步骤如下：首先，对原时间序列进行平稳性检验，如果序列不满足平稳性条件，可以通过差分变换或者对数差分等其他变换，使原时间序列满足平稳性条件。
