35-4固体热容量的统计理论的研究
- 格式:doc
- 大小:396.00 KB
- 文档页数:12


混合法测固体比热容实验报告混合法测固体比热容实验报告引言固体比热容是描述物质热性质的重要参数,它能够反映物质在吸热或放热过程中的热容量大小。
本实验采用混合法测定固体比热容,通过测量固体与水混合后的温度变化,计算固体比热容。
本实验的目的是研究固体比热容的测定方法,并探讨不同固体的热容性质。
实验方法1. 实验装置本实验采用热量计法测定固体比热容,实验装置主要包括恒温水槽、温度计、电热器和热量计。
2. 实验步骤(1)将恒温水槽中的水加热至恒定温度,保持水温稳定。
(2)将待测固体样品称量并记录其质量。
(3)将待测固体样品放入热量计中,并将热量计放入水槽中。
(4)记录热量计中水的初始温度,并将电热器通电加热水槽。
(5)当水温达到一定稳定温度后,记录热量计中水的最终温度,并关闭电热器。
(6)根据温度变化计算固体比热容。
实验结果与分析通过实验测量,我们得到了不同固体样品的质量和温度变化数据。
以铝为例,其质量为10g,初始温度为25℃,最终温度为35℃。
根据热量守恒定律,可以得到以下公式:m1c1ΔT1 = m2c2ΔT2其中,m1为水的质量,c1为水的比热容,ΔT1为水的温度变化,m2为固体的质量,c2为固体的比热容,ΔT2为固体与水的温度差。
根据上述公式,我们可以计算出铝的比热容为:c2 = (m1c1ΔT1) / (m2ΔT2)将实验数据代入计算,可得铝的比热容为0.897 J/g℃。
通过对其他固体样品的测量和计算,我们可以得到它们的比热容。
然后,我们可以对比不同固体的比热容数据,分析它们之间的差异。
这些差异可能与固体的物理性质、结构以及化学成分有关。
讨论与结论通过本实验,我们成功地采用混合法测定了固体的比热容。
通过对多个固体样品的测量和计算,我们得到了它们的比热容数据,并进行了比较和分析。
在实验过程中,我们发现不同固体的比热容数值存在差异。
这可能是由于它们的物理性质和化学成分不同所导致的。
例如,金属固体通常具有较低的比热容,而非金属固体的比热容则相对较高。

固体比热容的研究固体比热容是指固体以一定量的能量温度升高的大小。
研究固体比热容的作用十分重要,因为它可以提供重要的理论准则,有助于研究有关电磁、物理、化学等不同领域的物质性质。
近年来,相关领域的研究人员对固体比热容进行了大量研究,以更深入地理解它的物理意义。
首先,科学家们使用不同的方法来表征固体比热容,例如交叉狄拉克方程(Cross-Dulwick equation)和普朗克方程(Prandtl equation)。
用这种方法,他们得出准确的结论,说明固体比热容可以表征物体的热态,它可以揭示物质的性质。
这些方法还可以用于计算固体比热容的最终值,以便准确的推断物质的性质。
其次,研究人员还利用不同的技术,开展了关于固体比热容的实验研究。
例如,他们使用金属片曲线及金属球来进行相关实验,研究不同温度下,金属物质的比热容是多少,以及它们如何变化。
此外,他们还通过电子衍射技术,对纳米固体进行检测,从而探究固体尺度上的比热容。
总之,近年来,研究人员对固体比热容的研究取得了很大进展,他们发展了许多不同的方法,以准确计算和检测固体比热容,取得了宝贵的结论。
此外,对固体比热容的研究,也有助于探究物质的性质,为大自然的研究奠定基础。
Scientists have conducted extensive research on the solid specific heat capacity in recent years in order to gain a deeper understanding of its physical meaning.First, scientists use different methods to characterise solid specific heat capacity, such as Cross-Dulwick equation and Prandtl equation. With such methods, they can obtain accurate results that suggest that the solid specific heat capacity is indicative of the thermal state of the object and can reveal its properties. Thesemethods can also be used to calculate the ultimate value of solid specific heat capacity in order to make an accurate inference of a material’s properties.Second, researchers has also used different techniques to carry out experimental studies on solid specific heat capacity. For instance, they utilized metal strips curves and metal balls for relevant experiments to study the specific heat capacity of metal objects under different temperatures and how it changes. In addition, they also used electron diffraction techniques to detect nanosolids in order to explore the specific heat capacity on a solid scale.In conclusion, researchers have made significant progress in the research of solid specific heat capacity in recent years. They have developed various methods to accurately calculate and detect the solid specific heat capacity, yielding valuable conclusions. Moreover, research on solid specific heat capacity has also helped to explore material properties, thus laying a foundation for nature research.。
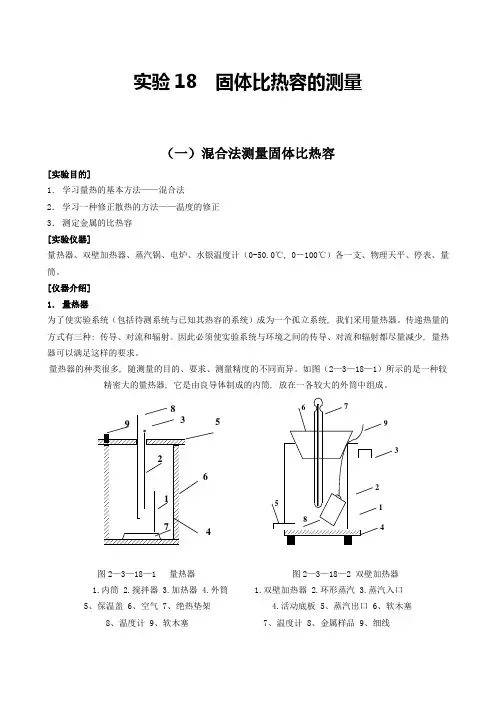
实验18 固体比热容的测量(一)混合法测量固体比热容[实验目的]1.学习量热的基本方法——混合法2.学习一种修正散热的方法——温度的修正3.测定金属的比热容[实验仪器]量热器、双壁加热器、蒸汽锅、电炉、水银温度计(0-50.0℃, 0-100℃)各一支、物理天平、停表、量筒。
[仪器介绍]1.量热器为了使实验系统(包括待测系统与已知其热容的系统)成为一个孤立系统, 我们采用量热器。
传递热量的方式有三种: 传导、对流和辐射。
因此必须使实验系统与环境之间的传导、对流和辐射都尽量减少, 量热2.外筒是双层结构, 空气封闭其中, 因为空气是热的不良导体, 故可避免空气传导而引起热量的损失;外筒上端的木盖可严密地盖着, 避免空气对对流所引起的热量损失;外筒的内壁和内筒的外壁均电镀得十分光亮, 可减少热辐射, 外筒的底部放上一个隔外筒的外表再包一层绒布, 这样就能使整个系统尽可能根据上述测量的T-t数据, 以T为纵坐标, 以t为横坐标, 即得如图(2—3—18—4)的T-t曲线。
A点对应的时刻就是测水温开始的时间 , B点对应的时刻就是, 而不是5分钟末的时间。
然后作图即得混合前后冷水的初温和末温T。
把各个物理量的测量值代入式(2-3-18-1)即可算出金属样品的比热容。
图(2—3—18—4)中的G点所对应的温度应为室温所在的位置, 这样才不影响温度的修正。
[实验内容和要求]1. 混合法测定铜块的比热容2.混合过程中散热的温度修正法3.混合前量热器(含水)系统温度低于室温(加冰块), 测量系统随时间吸热变化的温度。
4. 混合过程快速测量变化的温度5. 数据处理:Cx与标准值求百分误差[注意事项]1. 作温度值修正法曲线图, FE垂直于t轴, 满足S1=S2, 图中G点对应的温度接近室温为佳。
2. 从曲线图中定出初温T2和末温T。
[实验思考]请分析本实验主要的误差来源。
(二)冷却法测量金属的比热容[实验目的]学习冷却法测量金属比热容的方法[实验仪器]FB312型冷却法金属比热容测量仪[实验原理]根据牛顿冷却定律, 用冷却法测定金属的比热容是量热学常用方法之一。


讨论固体中原子、电子对热容量的贡献固体是由原子或者分子组成的物质,其热容量是指在加热过程中吸收热量的能力。
热容量的大小反映了固体内部粒子的运动自由度,包括原子和电子的运动。
在固体中,原子和电子对热容量的贡献有着不同的特点和机制。
首先,我们来讨论原子对固体热容量的贡献。
固体中的原子由于受到晶格的限制,其运动仅限于振动,即原子在平衡位置附近做小幅度的振动。
这种振动称为晶格振动或者声子振动。
由于原子振动的自由度有限,因此原子对固体热容量的贡献很小。
然而,随着温度的升高,原子的振动会增强,其能量和热容量也会增大。
根据经典统计物理学的理论,固体的热容量与温度的关系可以由爱因斯坦模型或者德拜模型来描述。
爱因斯坦模型假设固体中的每个原子都具有相同的振动频率,且原子之间没有相互作用。
这个模型对于描述固体的低温热容量是比较准确的,但是在高温下的热容量预测就不太准确了。
爱因斯坦模型预测的固体热容量与温度的关系可以用以下公式表示:Cv = 3Nk [(θE / T)^2 exp(θE / T)] / [(exp(θE / T) - 1)^2]其中,Cv表示固体的摩尔热容量,N表示固体中的原子数目,k是玻尔兹曼常数,θE是爱因斯坦温度,T是绝对温度。
德拜模型更为复杂,它考虑了固体中的原子之间的相互作用。
德拜模型假设固体中的原子之间可以发生相互作用,且每个原子的振动频率不一样。
德拜模型可以更好地解释高温下固体热容量的行为。
德拜模型预测的固体热容量与温度的关系可以用以下公式表示:Cv = 3R [(T / θD)^3 ∫0θD/(T / θD) (x^4 exp(x) / (exp(x) - 1)^2) dx]其中,Cv表示固体的摩尔热容量,R是气体常数,θD是德拜温度,T是绝对温度。
除了原子振动对热容量的贡献外,固体中的电子也对热容量有贡献。
电子是固体中带有负电荷的粒子,其能量受到晶格势场的制约。
在固体中,电子可以在能带中自由运动,其能量由费米能级决定。


热力学实验探索热容量与比热容的实验测量与数据分析热容量和比热容是描述物质热学性质的重要参数,它们在热力学领域有着广泛的应用。
本文将通过热力学实验的方法,探索热容量与比热容的实验测量与数据分析。
一、实验目的研究物质在不同温度下的热容量及比热容,了解物质的热学性质。
二、实验原理热容量是指物体在温度变化时吸收或放出的热量与温度变化的比值。
比热容则是指单位质量物体的热容量。
根据热力学理论,热容量和比热容可通过测量物体的温度变化和吸热量来求得。
三、实验器材与试剂1. 热容量比较器2. 温度计3. 热源4. 实验物体:可以使用金属块或液体等不同材料。
四、实验步骤1. 热容量测量:步骤一:取一块给定材料的金属块,称量其质量并记录。
步骤二:将金属块放入热容量比较器中,并使其与热源接触。
步骤三:利用温度计测量金属块的初始温度,并记录。
步骤四:启动热源,使金属块受热。
步骤五:记录金属块在不同时间点的温度,直到温度变化趋于稳定。
步骤六:根据测量数据,计算金属块的热容量。
2. 比热容测量:步骤一:取一定质量的液体(如水),称量并记录。
步骤二:将液体放入热容量比较器中,并接触热源。
步骤三:使用温度计测量液体的初始温度,并记录。
步骤四:启动热源,使液体受热。
步骤五:记录液体在不同时间点的温度,直到温度变化趋于稳定。
步骤六:根据测量数据,计算液体的比热容。
五、实验数据分析1. 热容量数据分析:将实验测得的金属块温度随时间变化的数据绘制成温度-时间曲线。
根据曲线的斜率,计算金属块的热容量。
热容量的单位为焦耳/摄氏度。
2. 比热容数据分析:将实验测得的液体温度随时间变化的数据绘制成温度-时间曲线。
根据曲线的斜率,计算液体的比热容。
比热容的单位为焦耳/克·摄氏度。
六、结果与讨论根据实验测得的数据,可以得到不同物质的热容量和比热容值。
比较不同物质的热容量和比热容,可以探索物质的热学性质和热传导能力。
比如,金属块的热容量通常较大,而液体的比热容通常较大。

3.3 固体热容的量子理论一. 经典理论二. 爱因斯坦模型(Einstein 1907年)D b1912三. 德拜模型(Debye 1912年)四. 实际晶体的热容参考:黄昆书 3.8节(p122-132)Kittel 书5.1节(79-87)前面提到:热容是固体原子热运动在宏观性质上的最直接体现,因而对固体原子热运动的认识实际上首先是从固体热容研究开始的。
我们讨论固体热容仍是以揭示原子热运动特征为目的,而完整地介绍热容统计理论应是统计物理的内容。
而完整地介绍热容统计理论应是统计物理的内容固体热容由两部分组成:部分来自晶格振动的贡献,称为固体热容由两部分组成:一部分来自晶格振动的贡献称为晶格热容;另一部分来自电子运动的贡献,称为电子热容。
除非在极低温度下,电子热容是很小的(常温下只有晶格热容的1%)。
这里我们只讨论晶格热容。
经典理论的失败固体比热Dulong-Petit 定律曾在多年间被用作量度原子质量的一种技巧,然而,后来詹姆斯·杜瓦及海因里希·夫里德里希·韦伯的研究表明杜隆-珀蒂定律只于高温时成立;在低温时或像金刚石这种异常地硬的固体,比热还要再低一点。
在低温时或像金刚石这种异常地硬的固体热要再低点双原子气体比热气体比热的实验观测也引起了对均分定理是否有效的质疑。
定理预测简单单元子气体的摩尔比热容应约为3cal/(mol·K),而双原子气体则约为()7cal/(mol·K)。
实验验证了预测的前者,但却发现双原子气体的典型摩尔比热容约为5cal/(mol·K),并于低温时下跌到约3cal/(mol·K)。
麦克斯韦于1875年指出实验与均分定理的不合比这些数字暗示的要坏得多。
金属的比热根据古典德鲁德模型,金属电子的举止跟几乎理想的气体一样,因此它们应该向(3/2)NekB 的热容,其中Ne 为电子的数量。
不过实验指出电子对热容的供给并不多很多的金属的摩尔比热容与绝缘体几乎样给并不多:很多的金属的摩尔比热容与绝缘体几乎一样。

固体热容的计算方法发展史固体热容是指单位质量的物质在温度变化下所吸收或释放的热量。
它是研究固体热力学和热传导性质的重要参数。
固体热容的计算方法的发展历史可以追溯到18世纪。
在18世纪,拉瓦锡通过实验测定了金属的热容,并提出了一个简单的近似计算公式:C=αT,其中C为热容,α为比热系数,T为温度。
这个公式在当时的实验条件下得到了比较好的近似。
然而,随着温度的升高,尤其是在高温下,这个公式的适用性变得较差。
19世纪,热力学的发展推动了固体热容计算方法的改进。
杜朗-珀托热容定理(Dulong-Petit theorem)提供了一种计算金属热容的近似方法。
根据该定理,金属的原子热容近似等于 3R,其中 R 为普适气体常量。
这个方法适用于大多数金属,但在低温下和其他一些特殊条件下效果变差。
20世纪初,爱因斯坦对于低温下固体热容的行为提出了一个理论模型,即爱因斯坦模型。
他假设固体是由一系列简谐振动子组成,每个振动子在不同的能级上分布,并服从玻尔兹曼分布。
通过对振动频率进行积分,可以计算出固体的热容。
这个模型在低温下对实验结果的拟合效果比较好。
随着量子力学的发展,德拜模型在固体热容计算中被引入。
德拜模型将固体看作是一系列具有离散能级的振动子,这些振动子的分布以及振动频率通过量子力学的方法进行计算。
德拜模型对于低温下的固体热容计算有较好的效果,但在高温下仍然存在差异。
近年来,随着计算机的快速发展,分子动力学模拟和密度泛函理论等计算方法的应用推动了固体热容的计算精度的提高。
这些计算方法能够精确地计算出固体原子和分子的振动、旋转等运动的能量和频率。
通过对这些结果进行统计处理,可以得到固体热容的更准确的计算结果。
总结起来,固体热容的计算方法发展经历了拉瓦锡公式、杜朗-珀托热容定理、爱因斯坦模型、德拜模型以及计算机模拟等多个阶段。
这些方法在不同温度范围和条件下具有不同的适用性和精度,为固体热容的理论研究和实际应用提供了重要的理论基础和计算工具。

固体热容量的爱因斯坦理论如前所述,固体中原子的热运动可以看成3N 个振子的振动。
爱因斯坦假设这3N 个振子的频率都相同。
以ω表示振子的圆频率,振子的能量级为)21(+=n n ωε n=0,1,2,⋯ (7.7.1)由于每一个振子都定域在其平衡位置附近作振动,振子是可以分辨的,遵从玻耳兹曼分布,配分函数为ωβωβωβ --∞=+--==∑ee eZ n n 12)2/1(1 (7.7.2) 根据式(7.1.4),固体的内能为 1323l n 31-+=∂∂-=ωβωωβ e N N Z NU (7.7.3) 式(7.7.3)的第一项是3N 个振子的零点能量。
与温度无关;第二项是温度为T 时3N 个振子的热激发能量定容热容量C V 为 22)1()(3)(-=∂∂=kTkTV V ee kTNk T U C ωωω (7.7.4)引入爱因斯坦特征温度E θ ωθ =E k (7.7.5)可将热容量表为 22)1()(3-=T T EV EEe e TNk C θθθ (7.7.6)因此根据爱因斯坦的理论,C V 随温度降低而减少,并且C V 作为TEθ的函数是一个谱适函数。
现在讨论(7.7.6)式在高温和低温范围的极限结果。
当T E θ≥时,可以取近似。
由式得Nk C V 3= (7.7.7)式(7.7.7)和能量均分定理的结果一致。
这个结果的解释是,当T E θ≤时,能级间距远小于kT ,能量量子化的效应可以忽略,因此经典统计是适用的。
用经典统计和量子统计讨论固体的内能和热容量1.量子统计和经典统计的联系和区别建立在经典力学基础上的统计物理学称为经典统计物理学, 建立在量子力学基础上的统计物理学, 称为量子统计物理学。
近独立的费米粒子与玻色粒子构成孤立系统, 处于平衡时的量子统计分布规律分别遵从费米分布和波色分布, 玻色—爱因斯坦统计和费米—狄拉克统计是最基本的量子统计分布, 定域系统遵从玻耳兹曼分布律, 玻耳兹曼统计属半经典的统计分布。
运用玻耳兹曼统计, 对力学系统的平衡热性质作出了一些满意的解释, 推动了物理学的发展。
然而, 在发展过程中, 某些理论结果却与事实不符, 例如对气体和固体的热容量不能给出适当的解释。
应用经典统计理论研究平衡热辐射问题时, 理论结果与实验事实也不相一致。
20 世纪开始, 普朗克在他的黑体辐射公式中提出了量子概念, 首先动摇了经典物理学的观念, 后来爱因斯坦应用量子理论成功地解释了光电效应, 接着爱因斯坦、德拜等人应用量子理论成功地研究了固体的热容量, 获得了满意的结果, 到1925 年海森堡和薜定谔建立了量子力学之后, 人们才明确了在宏观运动中归纳总结的经典电动力学不能完全适用于微观运动, 而必须运用量子力学的规律对经典统计理论进行根本的改造, 因而, 随着量子力学的建立, 量子统计理论也同时形成并不断得到完善。
对经典系统或量子系统的随机运动过程而言, 在统计原理上并没有本质的差别, 所以, 量子统计仍以等概率原理为基本假设, 肯定系统的系综平均值等于实验观测的时间平均值这个统计等效原理以及认为平衡态下的系综分布函数形式与经典统计的形式一样, 量子统计与经典统计的根本区别, 在于它们的力学基础不同, 经典统计是以经典力学为基础, 而量子统计则是建立在量子力学的基础上, 这就导致对微观粒子运动的描述绝然不同。
2.固体内能的研究固体内能理论认为,低温内能U(T)<3NkT+U0,高温内能U(T)≈3NkT+U0[1]。
热力学中的热容量实验设计热容量是物质在温度变化下吸收或释放的热量与其温度变化之比,是热力学中重要的物性参数之一。
为了准确测量物质的热容量,我们需要设计一系列实验来获取可靠的数据。
本文将介绍一个用于测量热容量的实验设计。
一、实验目的本实验旨在测量物质在不同温度下的热容量,并通过实验数据分析热容量的变化规律,探究物质的热性质。
二、实验仪器与材料1. 热容量测定装置:包括热源、热浴、测温仪器等;2. 待测物质:选择具有热容量变化较明显的物质,如水或金属样品等;3. 实验记录工具:温度计、计时器等。
三、实验步骤与设计方案1. 实验准备a. 将待测物质制备成小块或液体状态,以便于加热和测温;b. 准备热容量测定装置,确保其正常运行。
2. 测定物质的初始温度a. 将待测物质置于室温环境中,等待其与环境温度达到平衡;b. 使用温度计测量待测物质的初始温度,记录在实验数据表中。
3. 加热过程a. 将待测物质加热至一定温度,可以采用加热器、电炉等热源;b. 加热至目标温度后,停止加热,并立即记录下物质的温度和时间。
4. 冷却过程a. 停止加热后,观察并记录待测物质的温度变化,直到温度趋于稳定;b. 记录下物质冷却至室温的时间。
5. 测定下一温度点a. 重复步骤3-4,分别将待测物质加热至不同的温度点,记录相关数据。
6. 数据处理与分析a. 将实验记录的温度与时间数据绘制成温度-时间曲线图;b. 通过曲线的斜率来计算出物质在不同温度下的热容量;c. 统计不同温度下的热容量数值,进行数据分析和解释。
四、实验安全注意事项1. 操作时要注意安全,避免烫伤和火灾等事故的发生;2. 加热过程中,检查仪器是否正常运行,避免温度过高导致仪器损坏;3. 操作精确、仪器准确是保证实验可靠性的关键。
五、实验结果与讨论通过实验设计,我们可以得到一系列温度-时间数据,并通过斜率计算得到物质在不同温度下的热容量。
分析实验结果可以发现不同物质的热容量存在差异,并且随温度的升高或降低而变化。
对固体比热容的研究陈芳蕊(天水师范学院 物理系 甘肃,天水 741000 )摘要:固体比热容根据能量均分原理可得其定容比热容应为Nk C v 3= 在室温下与杜隆—珀蒂定律相符,但在低温范围内偏离杜隆—珀蒂定律,温度越低,比热容越小。
固体的定容比热容v C 包括晶格比热容和电子比热容两方面。
由于这两方面之间相互作用很弱,所以在本文中,从经典统计理论和量子统计理论出发将分别讨论晶格振动和电子热运动对固体比热容的贡献,并加以比较作出结论。
关键词:固体 温度 比热容The research on the specific heat capacity of solidChenfangrui(College of Physics and Information Science, Tianshui Normal University ,Tianshui ,741000)Abstract: The solid may result in its specific heat at constant volume compared to the heat capacity according to the equipartition of energy principle to accommodate is Nk C v 3=Under room temperature with Du prosperous - Podi law match case, but deviates Du in the low temperature scope the prosperous - Podi law, the temperature is lower, is smaller than the heat capacity. The solid specific heat at constant volume accommodates including the crystal lattice compares the heat capacity two aspects compared to the heat capacity and the electron. Because between these two aspects the interaction is very weak, therefore in this paper, will embark from the classics statistical theory and the quantum statistics theory will discuss the lattice vibration and the electronic heat movement separately compares the heat capacity to the solid the contribution, and will compare draws the conclusion.Key words: Solid Specific heat capacity Temperature1.引言固体比热容是指单位质量的物质在某一过程温度升高1K 所吸收的热量,也是特定粒子(电子、原子、分子等)结构及其运动特性的宏观表现。
固体热容两种物理模型的分析和比较宋学丽【摘要】固体热容是反映晶体热学性质的一个重要物理量,对固体热容的具体求解是一个相当复杂的问题,在一般讨论中,常采用爱因斯坦模型及德拜模型.其实验结果的理论解释是贯穿整个统计物理学的一个重要问题,由于假设模型的不同导致所得的结果各自有自己不同的特点.分别针对两种模型在高温和低温时的特点进行分析和讨论,并把两种模型进行对比,分析理论与实验出现差异的原因.对进一步理解两种模型的物理思想,及其讨论具体问题的方法具有重要意义.【期刊名称】《赤峰学院学报(自然科学版)》【年(卷),期】2010(026)012【总页数】2页(P143-144)【关键词】爱因斯坦模型;德拜模型;固体热容;金属固体【作者】宋学丽【作者单位】锡林郭勒职业技术学院,机械与电力工程系,内蒙古锡盟026000【正文语种】中文【中图分类】O469固体热容的实验结果的理论解释是贯穿整个统计物理的一个重要问题,通过对爱因斯坦模型和德拜模型进行理论计算所得结果的分析,爱因斯坦模型和德拜模型分别在高温和低温时表现出各自的特点.按照经典玻尔兹曼统计定容热容量为3Nk恒量[1-3].而实验上当低温时却趋于零.爱因斯坦模型和德拜模型在高温时都与实验结果一致,但低温时爱因斯坦模型趋于零的速度过快,而德拜模型在低温时以的方式趋于零的结果与实验符合的很好.通过对两种模型的对比可以对固体热容有更深的认识.爱因斯坦首先用量子理论分析固体热容量[4,5,7]的问题,成功的解释了固体热容量随温度下降[1-3]的实验事实.爱因斯坦把固体中原子的热容看成3 N个振子的振动假设这3 N个振子的频率都相同,所以有,定域遵从玻尔滋曼分布,所以振子的配分函数为:内能热容令(1)当高温时,T>>θE,CV=3 NK这个结果与经典所得的结果是一致的.(2)当低温时结果与实验定性相符,但是在定量上符合的不好.德拜模型[4,5,7]认为,固体是各向同性的连续弹性介质,固体中的原子或离子集体微振动,在固体中形成了各种频率与波矢量k的弹性驻波,整个固体的热振动能量为各种弹性驻波的能量之和,即在固体中原子产生的弹性驻波属于声波,因此声波场的能量也是量子化的,以hv为单位增减能量,我们把声波场能量的最小单位叫‘声子’[8],可以把声子看成粒子,但又不同与真实粒子,所以称为准粒子.声子的能量和动量分别为ε=hv,p=hk对应的弹性波可分为纵波与横波,横波有两个分量代表两个偏振方向,纵波与横波波速不同,因此声子可分为纵波声子与横波声子,能量和动量的关系分别为E=clp,E=ctp,在简谐近似下,各种弹性驻波是相互独立的,所以各种频率的声子之间没有相互作用,且处在某一状态的声子数是任意的,所以声子是理想的玻色气体,由于声子可以不断产生和消灭,所以声子数不守恒,即声子气体的化学势为零.于是温度为T时处在能量为hv的一个量子态的平均声子数为由此可知,温度为T时的内能为其中Φ0表示所有原子都位于平衡位置时原子之间的相互作用势能,上式中第二项为声子的总能量,即温度为T时固体热运动的能量.因此在体积v内,频率在v-v+dv之间的声子(包括纵波声子和横波声子)的量子态数为由于固体中有N个原子或离子,共3 N个自由度,相应的有3 N的独立的弹性驻波,即声子的量子态总数为3 N,于是有因此其中固体内能可表示为即令于是有其中(1)高温极限[6]这正是经典玻尔滋曼统计理论所推出的能均分定理的结果.(2)低温极限[6]:T<<θD,则有U=U0+3 Nk·上式称为T3定律.两种热容量各有不同的特征,爱因斯坦模型高温时符合实验(CV=3 Nk),低温时热容趋于零的速度过快,是定性相符,定量符合的不好.原因是爱因斯坦模型认为所有谐振子都取同一频率太简化了.德拜模型高温时符合实验(CV=3 Nk),低温时符合T3律,对于金属固体德拜模型在3 K以下不符,原因是3 K以下电子对热容的贡献不可忽略.图中画出了爱因斯坦理论(虚线),德拜理论(实线),和铜的实验结果(圆圈),以作比较.固体中真实的粒子是原子,由于原子间的强烈相互作用,如果直接去处理他们,问题会变得很复杂,德拜在引入声子[8]概念后,使得模型十分形象,问题也大为简化,目前这种准粒子的方法已成为处理耦合着的多粒子系统的很有效的方法.【相关文献】〔1〕汪志诚.热力学统计物理[M].北京.高等教育出版社,1980.〔2〕马本坤,高尚惠.热力学与统计物理[M].北京.高等教育出版社,1986.〔3〕梁希侠,班士良.统计热力学[M].内蒙古:内蒙古出版社,2001.〔4〕黄昆,韩汝琦.固体物理学[M].北京:高等教育出版社,2005.〔5〕王矜奉.固体物理学教程[M].济南:山东大学出版社,1999.〔6〕王矜奉,范希会,张承琚.固体物理概念和习题指导[M].济南:山东大学出版社,2005.〔7〕方俊鑫,陆栋.固体物理学[M].上海科学技术出版社,1980.〔8〕李正中.固体理论(第 2版)[M].北京:高等教育出版社,2002.。
固体统计力学固体统计力学是一门研究物理学基本规律的学科,其研究对象为固体物质。
固体物质的核心特点是分子或离子排列有序,且相互之间的相互作用较强,因此固体物质具有较高的稳定性和较强的电学和热学性质。
固体统计力学主要研究固体粒子的排列和相互作用规律,以及温度、压力等环境条件对固体的影响。
下面将从三个方面分别介绍固体统计力学的研究内容。
一、固体物质的基本结构固体物质的基本结构特征是原子、分子、离子等微观粒子按照规则排列形成的固态晶体。
因为固体粒子排列有序,因此不同于气体和液体,固体物质的各种性质呈现出明显的方向性或者周期性,例如晶体的各种物理性质都具有方向性,常常可以用周期性函数来表示。
除了晶体之外,还有非晶态固体。
非晶态固体的粒子在空间上并没有有序排列,而是具有一定的随机性,因此其物理性质并不呈现出明显的周期性。
二、固体物质的热学性质固体物质的热学性质与温度、压力等环境条件密切相关。
在固体中,粒子之间的相互作用很强,因此温度较低时固体物质表现出很大的弹性形变,当温度升高到一定程度时,则会发生热膨胀、热压缩等热力学现象。
固体物质的热学性质主要包括热容、热导率、热膨胀系数等指标。
其中热容代表固体物质在吸收一定热量时的温度升高程度,热导率代表固体物质传递热能的能力,热膨胀系数则代表固体物质在温度变化时的体积变化率。
固体物质的电学性质主要包括导电性、介电常数、电阻率等指标。
固体物质的导电性与其电子的自由度密切相关。
一般来说,具有自由电子的金属材料具有良好的导电性,而没有自由电子的电介质则没有导电性。
介电常数表示电介质中电荷的运动所受到的阻力程度,电阻率则代表固体物质中电荷运动的难易程度。
电学性质对于固体物质的应用十分重要,例如半导体材料和金属材料具有不同的导电性能,因此可以广泛地应用于电子器件、光电子器件等领域。
总之,固体统计力学研究物质的基本结构以及其热学、电学性质,对于推动物理学的发展、解决实际问题以及促进科学技术的进步都有着重要的作用。
学科代码:0702学号:2007052011 铜仁学院本科学生毕业论文题目:固体热容理论的研究系别:物理与电子科学系专业:物理学年级:2007级学生:符东欧指导老师:宋谋胜完成时间:2011年5月10日固体热容理论的研究符东欧摘要:固体热容量是物质热性质的重要参量之一,也是研究材料热性质最基本的根据与内容之一。
从而对固体热容的研究就显得十分重要。
本文将用归纳总结从经典统计理论到量子统计理论的过程去研究两种理论的建立背景、应用范围与条件,分析二者的互关系、二者的局限性以及各自的应用情况。
得出经典热容理论与量子热容理论两者的成功与不足,可见热容理论还不完善从而使本文为今后对固体热容的研究提供一定的理论基础。
关键字:热容;经典理论;爱因斯坦模型;德拜模型;Study of Solid heat capacity theoryDong ou FuAbstract:Solid heat capacity is an important parameter material thermal properties, and also one of the most basic research material thermal properties of according and one of the contents.So the study of solid heat capacity becomes very important. This paper from the classical statistical theory to quantum statistical theory to study the process of the two theories of building background, application range and conditions, analysis of both the limitations of mutual relations, both and their application. Heat capacity that classical theory and quantum theory of heat capacity of both success and inadequacy ,visible heat capacity theory is not perfect so this paper for future research on solid heat capacity provide certain theoretical basis.Key words:Heat capacity Classical theory Einstein model Debye model一. 引言在20世纪末期对固体热容的研究比较少。
可以知道在常温度下,电子气的摩尔比热容与晶格振动的摩尔比热相比较是很小的,可以忽略不计,因此金属的比热容遵从Dulong-petit定律,即平时给出的固体比热容的数值时固体金属定压比热容数值的平均值[1-3]。
对金属材料,比热容由晶格振动和电子两部分的贡献的。
在常温下,主要考虑晶格振动的贡献;在低温下,电子对比热容的贡献起主要作用[4-6]。
在实温下,某些固体的比热容远小于经典值,在低温下比热容是随温度的降低而降低是经典热容理论的不足。
进入21世纪后人们对固体比热容的研究越来越重视,研究它的人也越来越多。
先给出固体热容量的实验规律,再用近代量子统计理论对金属中自由电子运动和晶格振动对固体热容量产生的影响作了定量分析[7]。
运用比较和归纳方法,从微观粒子的二象性,测不准原理,全同性原理,微观粒子运动状态描述和对应定理几方面阐述了量子统计与经典统计之间的区别与联系。
以及从经典统计理论发展到量子统计理论的推导解释过程中,可以看出经典统计理论局限的突破,是热现象理论发展的必要也是量子理论产生的必然[8-9]。
从确定了晶体的Debye 温度随温度变化的普适关系,导出在此关系下晶体热力学函数的表达式,在这基础上对铟的德拜温度和定压热容量随温度变化的规律,得出在高温和低温的理论值与实验符合得较好,在中间段符合得较差。
通过对德拜模型的研究,分析了利用德拜模型解决金属固体热容量与实验结果不一致的原因,并且研究了金属自由电子气对热容量的贡献,最终达到了由统计理论得到的金属固体热容量与实验结果一致的结论[10-13]。
目前,在研究固体热力学性质尤其是研究固体热容量随温度的变化时,许多文献都把德拜温度看作常数来处理,其理论结果与实验结果有所偏差.大量实验研究表明:系统的德拜温度与温度.压强.体积有关.可见固体热容理论还够不完善.固体热容量是物质热性质的重要参量之一,也是研究材料热性质最基本的根据与内容之一。
对它的研究经历了从经典统计理论到量子统计理论的过程,然而这两种理论均有各自的应用范围,只有在给定的条件下才适用.尽管二者的理论计算结果与实验有不同程度的偏差,但量子统计理论对热容量的究更与实验结果相符合。
因此,本文通过研究两种理论的建立背景、应用范围与条件,分析二者的相互关系、二者的局限性以及各自的应用情况。
二. 经典热容理论2.1 能量均分定理玻耳兹曼在经典条件下得的玻耳兹曼分布,在满足其分布下由经典力学知道粒子的能量是动能p ε和势能q ε之和。
动能可以表示为动量的平方项之和:2112ri pi i p a ε==∑ (2-1)21112a p 的平均值为: 2111110 (1111222)r r r dq dq dp dp a p e kT Z h βεβ-=⋅=⎰ (2-2) 假如势能中有一部分可表示为平方项:()'''2111,,2r i i r q q r i b q q q εε+==+∑则可同样证明(i q 的积分限是-∞到+∞):2111122b q kT =⋅ (2-3)这样就证明了,能量ε中每一个平方项的平均值等于12kT ⋅。
2.2 经典统计理论的热容量经典统计理论把固体中各个原子在它们各自的平衡位置附近作微小的简谐振动看成是彼此独立的。
设固体的总原子数为N ,把原子看成质点,则系统共有3N 个自由度。
除去整个固体作为刚体而有的3个平动和3个转动自由度,总振动自由度为3N-6个。
当1>>N 时,3N -6≈3N ,则固体的微观总能量为:301Nii E E ε==+∑ (2-4)其中i ε为第i 个振动自由的能量,其经典形式为:222122i i i p m q m εω=+ (2-5)()00E E V =是固体原子处于平衡位置时的总能量,既固体的结合能,它是体积的函数。
由经典统计的能量均分定理得到每一个振动自由度的平均能量等于KT ε=,故有:03E NkT E =+ (2-6)3v VE C Nk T ⎛⎫∂== ⎪∂⎝⎭ (2-7)2.3 经典热容理论的应用、局限性.经典统计理论的热容量是在全经典力学下推导得出的,从(2-7)式可以看出固体热容的经典理论给出的热容是一个与温度无关的恒量.这结果在高温和实温范围内与实验测量值相符合,这也与Pearl DuLong - for law 一致。
在经典统计理论中粒子遵从波尔兹曼分布,如已知粒子遵从经典波尔兹曼分布,其能量表达式为:()222212x y z p p p ax bx m ε=++++ ()bX aX p p p mz y x ++++=222221ε 其中a 、b 是常数,则粒子的平均能量为ε⎛⎫=- ⎪⎝⎭21424b kT a 。
上面是经典统计理论的成功之处,然而在低温下固体热容量的实验测量表明,固体的热容量随温度的降低而减少.并在0T =时变为零.固体热容的低温特性可用下面的关系式[11]表示:3v C T T αγ=+α、γ均为常数,这一关系是经典理论所不能解释的。
1900年普朗克在处理黑体辐射时提出能量量子化的假说以后,有几年时间并未引起物理学界的重视。
是爱因斯坦首先提出量子概念有更广泛的应用,在1906年爱因斯坦用量子理论来解决固体比热的问题[6-7]。
如在经典的固体比热理论暴露出来的问题,例如:在实温下,某些固体的比热容远小于经典值。
既比热容并非是像经典统计理论得出的是常数,在低温下比热容是随温度的降低而降低。
爱因斯坦认识到,经典统计理论的问题出在能量均分定理在低温下不适用。
三. Einstein 热容理论3.1 Einstein 模型爱因斯坦模型:爱因斯坦把固体中原子的热运动看成3N 个振子的振动,并且这3N 个振子的频率都相同。
3.2 Einstein 热容量设ω为振子的圆频率,则振子的能级为:12n n εω⎛⎫=+⎪⎝⎭n=0、1、2、…由于每一个振子都定域在其平衡位置附近作振动,振子是可以分辨的,遵从波尔兹曼分布。
其配分函数为:211eZ e βωβω--=- (3-1) 由内能的统计表达式:1ln U NZ β∂=-∂ (3-2) 由 (3-1)式和 (3-2)得固体的内能为:133ln 321N U NZ N e βωωωβ∂=-=+∂- (3-3) (3-3)式中的第一项为3N 个振子的零点能量、第二项为温度在T 时刻3N 个振子的热激发能量。
定容热容量v C 为:2231kTv v kTU e C Nk T kT e ωωω∂⎛⎫⎛⎫== ⎪ ⎪∂⎝⎭⎝⎭⎛⎫- ⎪⎝⎭(3-4)引入爱因斯坦特征温度E θ,并令E k θω= 则热量为:2231EETE vTeC Nk T e θθθ⎛⎫= ⎪⎝⎭⎛⎫- ⎪⎝⎭(3-5)可见v C 随温度降低而减少,并且v C 作为ETθ的函数是一个普适函数。
对 (3-5)式在高温(E T θ )和低温(E T θ )的范围内进行讨论。
当E T θ时,可以取近似1EE T e Tθθ-≈代入(3-5)式得:3v C Nk = (3-6)(3-6)式和能量均分定理的结果一致,因为在高温(E T θ )时,能级间距远小于kT ,能量量子化的效应可以忽略,可见经典统计是实用的。
当E T θ 时1EETT ee θθ-≈带入(3-5)式得:23E E Tv C Nk eT θθ-⎛⎫= ⎪⎝⎭(3-7) 由(3-7)式可知,当温度趋于零时,v C 也趋于零。
这个结论与实验结果定性符合,这是因为温度趋于零时,振子能级间距ω 远大于kT 。
3.3 Einstein 热容理论的应用、局限性.由于经典热容理论无法解释固体热容在低温下的情况的条件下,爱因斯坦首先用量子理论解释固体热容在低温下趋于零的问题,但是它与实验结果在低温下的情况还有偏差,它在高温下适用。