基于k-Means算法的文本聚类(python实现)

利⽤Python如何实现K-means聚类算法⽬录前⾔算法原理⽬标函数算法流程Python实现总结前⾔K-Means 是⼀种⾮常简单的聚类算法(聚类算法都属于⽆监督学习)。

给定固定数量的聚类和输⼊数据集，该算法试图将数据划分为聚类，使得聚类内部具有较⾼的相似性，聚类与聚类之间具有较低的相似性。

算法原理1. 初始化聚类中⼼，或者在输⼊数据范围内随机选择，或者使⽤⼀些现有的训练样本(推荐)2. 直到收敛将每个数据点分配到最近的聚类。

点与聚类中⼼之间的距离是通过欧⼏⾥德距离测量得到的。

通过将聚类中⼼的当前估计值设置为属于该聚类的所有实例的平均值，来更新它们的当前估计值。

⽬标函数聚类算法的⽬标函数试图找到聚类中⼼，以便数据将划分到相应的聚类中，并使得数据与其最接近的聚类中⼼之间的距离尽可能⼩。

给定⼀组数据X1，...，Xn和⼀个正数k，找到k个聚类中⼼C1，...，Ck并最⼩化⽬标函数：其中是质⼼，计算表达式为上图a表达了初始的数据集，假设k=2。

在图b中，我们随机选择了两个k类所对应的类别质⼼，即图中的红⾊质⼼和蓝⾊质⼼，然后分别求样本中所有点到这两个质⼼的距离，并标记每个样本的类别为和该样本距离最⼩的质⼼的类别，如图c所⽰，经过计算样本和红⾊质⼼和蓝⾊质⼼的距离，我们得到了所有样本点的第⼀轮迭代后的类别。

此时我们对我们当前标记为红⾊和蓝⾊的点分别求其新的质⼼，如图4所⽰，新的红⾊质⼼和蓝⾊质⼼的位置已经发⽣了变动。

图e和图f重复了我们在图c和图d的过程，即将所有点的类别标记为距离最近的质⼼的类别并求新的质⼼。

最终我们得到的两个类别如图f。

当然在实际K-Mean算法中，我们⼀般会多次运⾏图c和图d，才能达到最终的⽐较优的类别。

算法流程注意点：1. 对于K-Means算法，⾸先要注意的是k值的选择，⼀般来说，我们会根据对数据的先验经验选择⼀个合适的k值，如果没有什么先验知识，则可以通过交叉验证选择⼀个合适的k值2. 在确定了k的个数后，我们需要选择k个初始化的质⼼，就像上图b中的随机质⼼。

K-means聚类算法及python代码实现K-means聚类算法（事先数据并没有类别之分！所有的数据都是⼀样的）1、概述K-means算法是集简单和经典于⼀⾝的基于距离的聚类算法采⽤距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越⼤。

该算法认为类簇是由距离靠近的对象组成的，因此把得到紧凑且独⽴的簇作为最终⽬标。

2、核⼼思想通过迭代寻找k个类簇的⼀种划分⽅案，使得⽤这k个类簇的均值来代表相应各类样本时所得的总体误差最⼩。

k个聚类具有以下特点：各聚类本⾝尽可能的紧凑，⽽各聚类之间尽可能的分开。

k-means算法的基础是最⼩误差平⽅和准则,其代价函数是：式中，µc(i)表⽰第i个聚类的均值。

各类簇内的样本越相似，其与该类均值间的误差平⽅越⼩，对所有类所得到的误差平⽅求和，即可验证分为k类时，各聚类是否是最优的。

上式的代价函数⽆法⽤解析的⽅法最⼩化，只能有迭代的⽅法。

3、算法步骤图解下图展⽰了对n个样本点进⾏K-means聚类的效果，这⾥k取2。

4、算法实现步骤k-means算法是将样本聚类成 k个簇（cluster），其中k是⽤户给定的，其求解过程⾮常直观简单，具体算法描述如下：1) 随机选取 k个聚类质⼼点2) 重复下⾯过程直到收敛 {对于每⼀个样例 i，计算其应该属于的类：对于每⼀个类 j，重新计算该类的质⼼：}其伪代码如下：******************************************************************************创建k个点作为初始的质⼼点（随机选择）当任意⼀个点的簇分配结果发⽣改变时对数据集中的每⼀个数据点对每⼀个质⼼计算质⼼与数据点的距离将数据点分配到距离最近的簇对每⼀个簇，计算簇中所有点的均值，并将均值作为质⼼********************************************************5、K-means聚类算法python实战需求：对给定的数据集进⾏聚类本案例采⽤⼆维数据集，共80个样本，有4个类。

kmeans文本聚类案例本篇文章将介绍一个kmeans文本聚类案例。

聚类是一种无监督的机器学习方法，它可以将数据集中相似的数据点分组在一起。

在文本聚类中，我们将文本数据集中的相似文本聚集在一起。

kmeans 是一种聚类算法，它将数据点分为 k 个不同的簇。

在本文中，我们将使用 kmeans 算法对一个文本数据集进行聚类分析，并展示聚类结果。

首先，我们需要准备一个文本数据集。

这里我们将使用一个包含1000 篇新闻文章的数据集。

我们可以使用 Python 中的 pandas 库读取和处理数据集。

接下来，我们需要对文本数据进行预处理，包括去除停用词、标记化、词干提取等。

然后，我们需要将文本数据转换为数值向量，以便于计算相似度。

这里我们将使用词袋模型，其中每个单词被视为一个特征，并计算每个文本中每个单词的出现次数。

然后，我们使用 TF-IDF（Term Frequency-Inverse Document Frequency）算法对每个单词进行加权，以便更好地区分重要单词和常见单词。

接下来，我们使用 kmeans 算法对文本数据进行聚类。

kmeans 算法的主要步骤是初始化 k 个聚类中心，然后将每个数据点分配到最近的中心。

接着，重新计算每个聚类中心的位置，并重复以上步骤，直到聚类中心的位置不再改变或达到预设的迭代次数。

最后，我们可以使用可视化工具对聚类结果进行展示，并对每个簇进行分析和解释。

通过聚类，我们可以发现相似主题或类别的文本，并对文本数据集进行分类和组织。

总之，使用 kmeans 算法进行文本聚类可以帮助我们更好地理解文本数据集中的结构和关系。

通过聚类分析，我们可以发现文本数据中的隐藏模式和趋势，并为后续的数据挖掘和分析提供有价值的信息。

kmeans聚类---（代码为：博客数据聚类）（python）kmeans聚类迭代时间远⽐层次聚类的要少，处理⼤数据，kmeans优势极为突出.。

对博客数据进⾏聚类，实验测试了: 层次聚类的列聚类（单词聚类）⼏乎要上1⼩时，⽽kmeans对列聚类只需要迭代4次！！快速极多。

如图：包含两个聚类的kmean聚类过程：总思路：将所有要聚类的博客，全部⽤word表⽰成⼀个向量，即每篇博客都是由单词组成的，然后形成了⼀个单词-博客的矩阵，矩阵⾥的权重值就是单词在当前博客出现的总次数。

这样kmeans就是要将这些词频矩阵进⾏聚类。

其实kmeans这⾥⽤到的距离相似度是⽤pearson。

聚类之前，先读取数据⽂件blogdata.txt.⽂本如下：源⽂件第⼀列是博客名。

第⼀⾏从第⼆列起，是这些博客的单词列表的所有单词。

所以这⾥便有个wordlist。

这⾥的博客内容全部⽤单词表⽰，从第⼆⾏开始，每⼀⾏都是表⽰⼀篇博客。

def readfile(filename):#取得⽂件的所有内容，⽤数组存⽂件的每⾏数据lines = [line for line in file(filename)]#获取矩阵的第⼀⾏数据，⽤数组列表columnames存储所有列名columnnames = []columnnames = lines[0].strip().split('\t')[1:] #从数组下标为1的开始取，不要下标为0的，因为下标为0，是“Blog”，删去，返回的是数组列表rownames = []data = []splitwords = []datatemp = []for line in lines[1:]: #从下标为1的line数组⾥取各⾏，即从矩阵第⼆⾏开始去splitwords = line.strip().split('\t')#每⾏的第⼀列是⾏名，rownames存的是所有⾏名rownames.append(splitwords[0])#剩下部分是该⾏对应的数据# data.append(splitwords[1:]) #这⾥数据虽然是数字，但添加的是string类型，但是应该改成添加float类型datatemp = [float(x) for x in splitwords[1:]] #即，datatemp存的是所有x的数组：[x]。

Python实现Kmeans聚类算法本节内容：本节内容是根据上学期所上的模式识别课程的作业整理⽽来，第⼀道题⽬是Kmeans聚类算法，数据集是Iris(鸢尾花的数据集)，分类数k是3，数据维数是4。

关于聚类聚类算法是这样的⼀种算法：给定样本数据Sample，要求将样本Sample中相似的数据聚到⼀类。

有了这个认识之后，就应该了解了聚类算法要⼲什么了吧。

说⽩了，就是归类。

⾸先，我们需要考虑的是，如何衡量数据之间的相似程度？⽐如说，有⼀群说不同语⾔的⼈，我们⼀般是根据他们的⽅⾔来聚类的（当然，你也可以指定以⾝⾼来聚类）。

这⾥，语⾔的相似性（或者⾝⾼）就成了我们衡量相似的量度了。

在考虑存在海量数据，如微博上各种⽤户的关系⽹，如何根据⽤户的关注和被关注来聚类，给⽤户推荐他们感兴趣的⽤户？这就是聚类算法研究的内容之⼀了。

Kmeans就是这样的聚类算法中⽐较简单的算法，给定数据样本集Sample和应该划分的类数K，对样本数据Sample进⾏聚类，最终形成K个cluster，其相似的度量是某条数据i与中⼼点的”距离”(这⾥所说的距离，不⽌于⼆维)。

基本思想KMeans算法的基本思想是初始随机给定K个簇中⼼，按照最邻近原则把待分类样本点分到各个簇。

然后按平均法重新计算各个簇的质⼼，从⽽确定新的簇⼼。

⼀直迭代，直到簇⼼的移动距离⼩于某个给定的值。

基本步骤K-Means聚类算法主要分为三个步骤：1，初始化k个聚类中⼼。

2，计算出每个对象跟这k个中⼼的距离（相似度计算，这个下⾯会提到），假如x这个对象跟y这个中⼼的距离最⼩（相似度最⼤），那么x属于y这个中⼼。

这⼀步就可以得到初步的k个聚类。

3，在第⼆步得到的每个聚类分别计算出新的聚类中⼼，和旧的中⼼⽐对，假如不相同，则继续第2步，直到新旧两个中⼼相同，说明聚类不可变，已经成功。

复杂度分析时间复杂度：O(tKmn)，其中，t为迭代次数，K为簇的数⽬，m为记录数，n为维数空间复杂度：O((m+K)n)，其中，K为簇的数⽬，m为记录数，n为维数初始质⼼的选择选择适当的初始质⼼是基本kmeans算法的关键步骤。

标题：探究K均值聚类算法在Python中的实际应用1. 介绍K均值聚类算法是一种常见的无监督学习算法，广泛应用于数据分析、模式识别和图像处理等领域。

本文将深入探讨K均值聚类算法在Python中的实际应用，并通过实例演示其在数据聚类中的效果和价值。

2. K均值聚类算法简介K均值聚类算法是一种基于计算距离的聚类方法，其核心思想是将数据集划分为K个簇，并使每个数据点都属于距离最近的簇中心。

通过迭代更新簇中心的位置，最终实现簇内数据点的相似性最大化，簇间数据点的相似性最小化。

K均值聚类算法的主要优点是简单易实现，但也存在对初始聚类中心敏感、对异常值敏感的缺点。

3. K均值聚类算法Python实现在Python中，我们可以使用scikit-learn库中的KMeans类来实现K均值聚类算法。

我们需要导入所需的库和模块，然后准备数据集并进行标准化处理。

接下来，我们可以通过KMeans类来拟合数据并进行聚类分析，最终得到每个数据点所属的簇标签。

4. K均值聚类算法实例分析我们以一个实际案例来演示K均值聚类算法的应用。

假设我们有一个包含多个维度的数据集，并希望将其划分为三个簇。

我们可以通过Python代码来实现K均值聚类算法，并可视化展示聚类结果。

通过分析实例，我们可以深入理解K均值聚类算法在实际应用中的效果和局限性。

5. 总结与展望本文通过深入探究K均值聚类算法在Python中的实际应用，对该算法的原理、实现和实例进行了全面评估。

通过此次学习，我们理解了K均值聚类算法在数据分析中的重要性和实用性。

但也需要注意到K均值聚类算法对初始聚类中心的敏感性，并且在处理大规模数据时的效率问题。

未来，我们可以进一步研究改进的K均值聚类算法及其在更多领域的应用。

6. 个人观点作为我的文章写手，我对K均值聚类算法的个人观点是，它是一种简单而有效的聚类算法，在实际应用中具有较好的效果。

但在处理大规模高维数据时，需要结合其他聚类算法来提高效率和准确性。

kmeans聚类算法代码K-means是一种经典的聚类算法，通过将数据划分为k个簇来实现聚类。

下面是一个Python实现的K-means算法代码示例：```pythonimport numpy as npdef kmeans(X, k, max_iters=100):#随机选择k个中心点centers = X[np.random.choice(range(len(X)), k,replace=False)]for _ in range(max_iters):#分配数据点到最近的中心点labels = np.argmin(np.linalg.norm(X[:, np.newaxis] - centers, axis=-1), axis=-1)#更新中心点位置new_centers = np.array([X[labels==i].mean(axis=0) for i in range(k)])#判断中心点是否变化很小if np.linalg.norm(new_centers - centers) < 1e-5:breakcenters = new_centersreturn labels, centers#测试代码X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4, 0]])k=2labels, centers = kmeans(X, k)print("Cluster labels:", labels)print("Cluster centers:", centers)```上述代码实现了K-means算法的一个简单版本。

输入数据`X`是一个二维数组，大小为(n_samples, n_features)，代表n_samples个样本的特征向量。

参数`k`表示要划分的簇的个数。

`max_iters`是最大迭代次数，默认为100次。

k-means聚类算法与Python实现代码k-means 聚类算法思想先随机选择k个聚类中⼼，把集合⾥的元素与最近的聚类中⼼聚为⼀类，得到⼀次聚类，再把每⼀个类的均值作为新的聚类中⼼重新聚类，迭代n次得到最终结果分步解析⼀、初始化聚类中⼼⾸先随机选择集合⾥的⼀个元素作为第⼀个聚类中⼼放⼊容器，选择距离第⼀个聚类中⼼最远的⼀个元素作为第⼆个聚类中⼼放⼊容器，第三、四、、、N个同理，为了优化可以选择距离开⽅做为评判标准⼆、迭代聚类依次把集合⾥的元素与距离最近的聚类中⼼分为⼀类，放到对应该聚类中⼼的新的容器，⼀次聚类完成后求出新容器⾥个类的均值，对该类对应的聚类中⼼进⾏更新，再次进⾏聚类操作，迭代n次得到理想的结果三、可视化展⽰利⽤ python 第三⽅库中的可视化⼯具 matplotlib.pyplot 对聚类后的元素显⽰（散点图），⽅便查看结果python代码实现import numpy as npimport matplotlib.pyplot as plt# 两点距离def distance(e1, e2):return np.sqrt((e1[0]-e2[0])**2+(e1[1]-e2[1])**2)# 集合中⼼def means(arr):return np.array([np.mean([e[0] for e in arr]), np.mean([e[1] for e in arr])])# arr中距离a最远的元素，⽤于初始化聚类中⼼def farthest(k_arr, arr):f = [0, 0]max_d = 0for e in arr:d = 0for i in range(k_arr.__len__()):d = d + np.sqrt(distance(k_arr[i], e))if d > max_d:max_d = df = ereturn f# arr中距离a最近的元素，⽤于聚类def closest(a, arr):c = arr[1]min_d = distance(a, arr[1])arr = arr[1:]for e in arr:d = distance(a, e)if d < min_d:min_d = dc = ereturn cif __name__=="__main__":## ⽣成⼆维随机坐标（如果有数据集就更好）arr = np.random.randint(100, size=(100, 1, 2))[:, 0, :]## 初始化聚类中⼼和聚类容器m = 5r = np.random.randint(arr.__len__() - 1)k_arr = np.array([arr[r]])cla_arr = [[]]for i in range(m-1):k = farthest(k_arr, arr)k_arr = np.concatenate([k_arr, np.array([k])])cla_arr.append([])## 迭代聚类n = 20cla_temp = cla_arrfor i in range(n): # 迭代n次for e in arr: # 把集合⾥每⼀个元素聚到最近的类ki = 0 # 假定距离第⼀个中⼼最近min_d = distance(e, k_arr[ki])for j in range(1, k_arr.__len__()):if distance(e, k_arr[j]) < min_d: # 找到更近的聚类中⼼min_d = distance(e, k_arr[j])ki = jcla_temp[ki].append(e)# 迭代更新聚类中⼼for k in range(k_arr.__len__()):if n - 1 == i:breakk_arr[k] = means(cla_temp[k])cla_temp[k] = []## 可视化展⽰col = ['HotPink', 'Aqua', 'Chartreuse', 'yellow', 'LightSalmon']for i in range(m):plt.scatter(k_arr[i][0], k_arr[i][1], linewidth=10, color=col[i])plt.scatter([e[0] for e in cla_temp[i]], [e[1] for e in cla_temp[i]], color=col[i])plt.show()结果展⽰总结到此这篇关于k-means 聚类算法与Python实现代码的⽂章就介绍到这了,更多相关k-means 聚类算法python内容请搜索以前的⽂章或继续浏览下⾯的相关⽂章希望⼤家以后多多⽀持！。

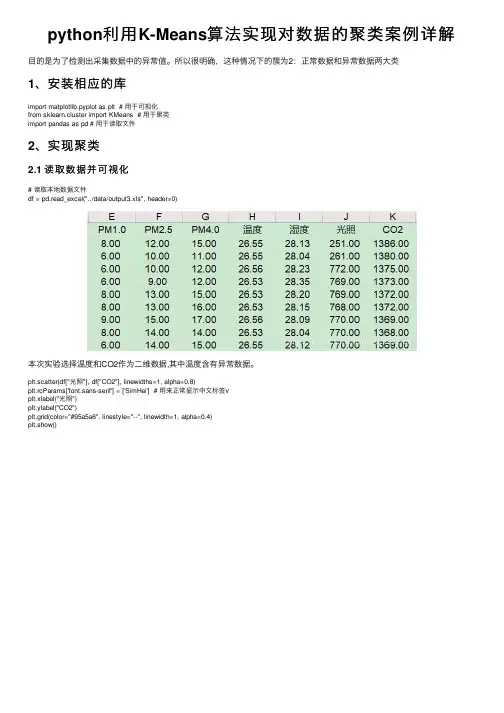
python利⽤K-Means算法实现对数据的聚类案例详解⽬的是为了检测出采集数据中的异常值。

所以很明确，这种情况下的簇为2：正常数据和异常数据两⼤类1、安装相应的库import matplotlib.pyplot as plt # ⽤于可视化from sklearn.cluster import KMeans # ⽤于聚类import pandas as pd # ⽤于读取⽂件2、实现聚类2.1 读取数据并可视化# 读取本地数据⽂件df = pd.read_excel("../data/output3.xls", header=0)本次实验选择温度和CO2作为⼆维数据,其中温度含有异常数据。

plt.scatter(df["光照"], df["CO2"], linewidths=1, alpha=0.8)plt.rcParams['font.sans-serif'] = ['SimHei'] # ⽤来正常显⽰中⽂标签vplt.xlabel("光照")plt.ylabel("CO2")plt.grid(color="#95a5a6", linestyle="--", linewidth=1, alpha=0.4)plt.show()2.2 K-means聚类设置规定要聚的类别个数为2data = df[["光照","CO2"]] # 从原始数据中选择该两项estimator = KMeans(n_clusters=2) # 构造聚类器estimator.fit(data) # 将数据带⼊聚类模型获取聚类中⼼的值和聚类标签label_pred = bels_ # 获取聚类标签centers_ = estimator.cluster_centers_ # 获取聚类中⼼将聚类后的 label0 和 label1 的数据进⾏输出x0 = data[label_pred == 0]x1 = data[label_pred == 1]plt.scatter(x0["光照"], x0["CO2"],c="red", linewidths=1, alpha=0.8,marker='o', label='label0') plt.scatter(x1["光照"], x1["CO2"],c="green", linewidths=1, alpha=0.8,marker='+', label='label1') plt.grid(c="#95a5a6", linestyle="--", linewidth=1, alpha=0.4)plt.legend()plt.show()附上全部代码import matplotlib.pyplot as pltfrom sklearn.cluster import KMeansimport pandas as pddf = pd.read_excel("../data/output3.xls", header=0)plt.scatter(df["光照"], df["CO2"], linewidths=1, alpha=0.8)plt.rcParams['font.sans-serif'] = ['SimHei'] # ⽤来正常显⽰中⽂标签vplt.xlabel("光照")plt.ylabel("CO2")plt.grid(color="#95a5a6", linestyle="--", linewidth=1, alpha=0.4)plt.show()data = df[["光照","CO2"]]estimator = KMeans(n_clusters=2) # 构造聚类器estimator.fit(data) # 聚类label_pred = bels_ # 获取聚类标签centers_ = estimator.cluster_centers_ # 获取聚类结果# print("聚类标签",label_pred)# print("聚类结果",centers_)# predict = estimator.predict([[787.75862069, 1505]]) # 测试新数据聚类结果# print(predict)x0 = data[label_pred == 0]x1 = data[label_pred == 1]plt.scatter(x0["光照"], x0["CO2"],c="red", linewidths=1, alpha=0.8,marker='o', label='label0')plt.scatter(x1["光照"], x1["CO2"],c="green", linewidths=1, alpha=0.8,marker='+', label='label1')plt.grid(c="#95a5a6", linestyle="--", linewidth=1, alpha=0.4)plt.legend()plt.show()到此这篇关于python利⽤K-Means算法实现对数据的聚类的⽂章就介绍到这了,更多相关python K-Means算法数据的聚类内容请搜索以前的⽂章或继续浏览下⾯的相关⽂章希望⼤家以后多多⽀持！。

Python KMeans 文本分类实例训练测试集1. 介绍文本分类是自然语言处理领域的一项重要任务，是将文本划分为不同的类别或标签的过程。

在本文中，我们将介绍如何使用 Python 中的KMeans 算法进行文本分类，对文本进行聚类以及对聚类结果进行评估。

2. 数据准备在进行文本分类之前，我们需要准备训练集和测试集。

我们可以使用已经标记好类别的文本数据作为训练集，然后使用未标记的文本数据作为测试集。

3. 数据预处理在将文本数据输入到 KMeans 算法之前，我们需要对文本数据进行预处理。

预处理包括文本分词、去除停用词、词干提取等步骤。

4. 特征提取在进行文本分类时，我们需要将文本数据转换成向量形式。

常用的特征提取方法包括词袋模型、TF-IDF 等。

这些方法会将文本数据转换成稀疏矩阵，以便进行聚类操作。

5. 模型训练使用 Python 中的 KMeans 算法对文本数据进行聚类。

KMeans 算法是一种基于距离的聚类算法，它将文本数据划分为 K 个类别，使得每个文本样本与所属类别的中心点的距离最小化。

6. 模型评估完成模型训练后，我们需要对聚类结果进行评估。

常用的评估指标包括轮廓系数、Calinski-Harabasz 指数等。

这些指标可以帮助我们评估模型的聚类效果，选择最优的 K 值。

7. 模型测试使用已经训练好的 KMeans 模型对测试集进行分类预测。

将测试集中的文本数据输入到模型中，得到文本所属的类别。

8. 结果分析分析分类结果，可以使用混淆矩阵、准确率、召回率等指标对分类结果进行分析和评估。

这些指标可以帮助我们了解模型的分类效果，找出分类错误的样本，优化模型性能。

总结在本文中，我们介绍了如何使用 Python 中的 KMeans 算法进行文本分类的实例训练和测试。

通过合理的数据准备、预处理、特征提取，以及模型训练、评估、测试和结果分析，我们可以得到一个高质量的文本分类模型，为文本数据的处理和应用提供了重要的参考。

Python机器学习之K-Means聚类实现详解本⽂为⼤家分享了Python机器学习之K-Means聚类的实现代码，供⼤家参考，具体内容如下1.K-Means聚类原理K-means算法是很典型的基于距离的聚类算法，采⽤距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越⼤。

其基本思想是：以空间中k个点为中⼼进⾏聚类，对最靠近他们的对象归类。

通过迭代的⽅法，逐次更新各聚类中⼼的值，直⾄得到最好的聚类结果。

各聚类本⾝尽可能的紧凑，⽽各聚类之间尽可能的分开。

算法⼤致流程为：（1）随机选取k个点作为种⼦点(这k个点不⼀定属于数据集)；（2）分别计算每个数据点到k个种⼦点的距离，离哪个种⼦点最近，就属于哪类；（3）重新计算k个种⼦点的坐标(简单常⽤的⽅法是求坐标值的平均值作为新的坐标值；（4）重复2、3步，直到种⼦点坐标不变或者循环次数完成。

2.数据及其寻找初步的聚类中⼼数据为Matlab加载格式（mat），包含X变量，数据来源为（⼤家可以去这），X为300*2维变量，由于是2维，所以基本上就是在平⾯坐标轴上的⼀些点中进⾏聚类。

我们⾸先构建初步寻找聚类中⼼（centroids，质⼼）函数，再随机设置初始质⼼，通过欧⽒距离初步判断X的每⼀个变量属于哪个质⼼。

代码为：import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as sbfrom scipy.io import loadmatdef find_closest_centroids(X, centroids):m = X.shape[0]k = centroids.shape[0] #要聚类的类别个数idx = np.zeros(m)for i in range(m):min_dist = 1000000 #迭代终⽌条件for j in range(k):dist = np.sum((X[i,:] - centroids[j,:]) ** 2)if dist < min_dist:# 记录当前最短距离和其中⼼的索引值min_dist = distidx[i] = jreturn idxdata = loadmat('D:\python\Python ml\ex7data2.mat')X = data['X']initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])idx = find_closest_centroids(X, initial_centroids)idx[0:3]在这⾥先⽣成m（这⾥为300）个0向量，即idx，也就是假设X的每个变量均属于0类，然后再根据与初始质⼼的距离计算dist = np.sum((X[i,:] - centroids[j,:]) ** 2)，初步判断每个变量归属哪个类，最终替代idx中的0.3.不断迭代寻找质⼼的位置并实现kmeans算法上述idx得到的300维向量是判断X中每个变量的归属类别，在此基础上，再对初始质⼼集群位置不断调整，寻找最优质⼼。

聚类算法python代码聚类算法是机器学习中常用的一种算法。

它将数据集中的数据根据某个相似度指标进行分类，使得同类别的数据距离更近，不同类别的数据距离更远。

本文将介绍用Python实现聚类算法（KMeans和DBSCAN）的步骤和代码。

聚类算法的步骤：1. 初始化：随机选择k个点作为质心，即每个质心代表一个聚类。

2. 分配：对于数据集中的每个点，根据距离最近的质心来分配所在的聚类。

3. 更新：重新计算每个聚类的质心。

4. 重复步骤2和步骤3，直到聚类不再发生改变。

KMeans算法的Python实现代码：```import numpy as npimport randomdef kmeans(data, k):# 随机初始化k个质心centroids = random.sample(list(data), k)n = len(data)# 初始化聚类标签和误差labels = [0] * nerrors = [np.inf] * nflag = Truewhile flag:flag = False# 分配：计算每个点距离每个质心的距离，选择距离最近的质心所在的类别for i in range(n):for j in range(k):distance = np.linalg.norm(data[i] - centroids[j])if distance < errors[i]:errors[i] = distancelabels[i] = j# 更新：重新计算每个类别的质心，并判断聚类是否发生改变for j in range(k):cluster = [data[i] for i in range(n) if labels[i] == j]if cluster:new_centroid = np.mean(cluster, axis=0)if not np.array_equal(centroids[j], new_centroid):centroids[j] = new_centroidflag = Truereturn labels, centroids```以上就是Python实现聚类算法（KMeans和DBSCAN）的步骤和代码。

Python实现的KMeans聚类算法实例分析本⽂实例讲述了Python实现的KMeans聚类算法。

分享给⼤家供⼤家参考，具体如下：菜鸟⼀枚，编程初学者，最近想使⽤Python3实现⼏个简单的机器学习分析⽅法，记录⼀下⾃⼰的学习过程。

关于KMeans算法本⾝就不做介绍了，下⾯记录⼀下⾃⼰遇到的问题。

⼀、关于初始聚类中⼼的选取初始聚类中⼼的选择⼀般有：（1）随机选取（2）随机选取样本中⼀个点作为中⼼点，在通过这个点选取距离其较⼤的点作为第⼆个中⼼点，以此类推。

（3）使⽤层次聚类等算法更新出初始聚类中⼼我⼀开始是使⽤numpy随机产⽣k个聚类中⼼Center = np.random.randn(k,n)但是发现聚类的时候迭代⼏次以后聚类中⼼会出现nan，有点搞不清楚怎么回事所以我分别尝试了：（1）选择数据集的前K个样本做初始中⼼点（2）选择随机K个样本点作为初始聚类中⼼发现两者都可以完成聚类，我是⽤的是iris.csv数据集，在选择前K个样本点做数据集时，迭代次数是固定的，选择随机K个点时，迭代次数和随机种⼦的选取有关，⽽且聚类效果也不同，有的随机种⼦聚类快且好，有的慢且差。

def InitCenter(k,m,x_train):#Center = np.random.randn(k,n)#Center = np.array(x_train.iloc[0:k,:]) #取数据集中前k个点作为初始中⼼Center = np.zeros([k,n]) #从样本中随机取k个点做初始聚类中⼼np.random.seed(5) #设置随机数种⼦for i in range(k):x = np.random.randint(m)Center[i] = np.array(x_train.iloc[x])return Center⼆、关于类间距离的选取为了简单，我直接采⽤了欧⽒距离，⽬前还没有尝试其他的距离算法。

def GetDistense(x_train, k, m, Center):Distence=[]for j in range(k):for i in range(m):x = np.array(x_train.iloc[i, :])a = x.T - Center[j]Dist = np.sqrt(np.sum(np.square(a))) # dist = np.linalg.norm(x.T - Center)Distence.append(Dist)Dis_array = np.array(Distence).reshape(k,m)return Dis_array三、关于终⽌聚类条件的选取关于聚类的终⽌条件有很多选择⽅法：（1）迭代⼀定次数（2）聚类中⼼的更新⼩于某个给定的阈值（3）类中的样本不再变化我⽤的是前两种⽅法，第⼀种很简单，但是聚类效果不好控制，针对不同数据集，稳健性也不够。

kmeans聚类算法python案例以下是一个使用K-means算法进行聚类的Python案例：```pythonimport numpy as npimport matplotlib.pyplot as pltfrom sklearn.cluster import KMeans# 生成随机数据（2个簇）np.random.seed(0)n_samples = 1000X = np.random.randn(n_samples, 2)# 使用K-means算法进行聚类n_clusters = 2kmeans = KMeans(n_clusters=n_clusters)kmeans.fit(X)y_pred = kmeans.predict(X)centroids = kmeans.cluster_centers_# 可视化聚类结果plt.scatter(X[:, 0], X[:, 1], c=y_pred)plt.scatter(centroids[:, 0], centroids[:, 1], marker='x', s=200, linewidths=3, color='r')plt.title("K-means Clustering")plt.show()```在这个案例中，我们使用`numpy`库生成了一个包含1000个样本的数据集，每个样本有两个特征。

然后，我们使用`scikit-learn`库的`KMeans`模型对数据进行聚类。

聚类的簇数设定为2。

最后，我们使用`matplotlib`库将聚类结果可视化展示出来，并将聚类中心用红色的"x"标记出来。

运行上述代码，你将会得到一个散点图，其中的散点被分成了两个簇，并且每个簇的中心点用红色的"x"标记出来。

kmeans python聚类实例K-Means Python聚类实例：从数据预处理到聚类结果解读引言：在机器学习和数据挖掘领域，聚类算法是一种常用的无监督学习方法。

其中，K-Means聚类算法是最常见和广泛使用的聚类算法之一。

它的主要思想是将数据集中的样本分成K个不同的簇或者组。

本文将为您详细介绍如何使用Python中的K-Means算法进行聚类分析，并解读聚类结果。

步骤一：数据预处理在进行聚类分析之前，我们首先需要对数据进行预处理。

这个步骤的目的是为了将原始数据转换成适合进行聚类分析的格式。

常见的数据预处理步骤包括数据清洗、特征选择和数据标准化等。

1. 数据清洗：数据清洗是指对原始数据进行缺失值处理或异常值处理。

在Python中，我们可以使用pandas库来进行数据清洗操作。

例如，可以使用dropna()函数删除缺失值，使用fillna()函数填充缺失值，使用isnull()函数判断是否存在缺失值等。

2. 特征选择：特征选择是指从原始数据中选择对聚类分析有意义的特征。

通过选择合适的特征，可以提高聚类结果的质量和解释性。

在Python中，我们可以使用sklearn库中的特征选择函数来进行特征选择。

例如，可以使用VarianceThreshold类删除方差低于阈值的特征，使用SelectKBest类根据某个评价指标选择K个最佳特征等。

3. 数据标准化：数据标准化是指通过对原始数据进行处理，将其转换为具有统一尺度和分布的数据。

这样做的目的是为了避免某些特征对聚类结果的影响程度过大。

在Python中，我们可以使用sklearn库中的StandardScaler类来进行数据标准化操作。

步骤二：K-Means聚类算法在完成数据预处理之后，我们可以开始进行K-Means聚类分析了。

K-Means算法的核心思想是通过迭代优化的方式将数据集中的样本分成K个不同的簇。

算法的步骤如下：1. 随机选择K个簇中心点。

利⽤python实现聚类分析K-means算法的详细过程K-means算法介绍K-means算法是很典型的基于距离的聚类算法，采⽤距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越⼤。

该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独⽴的簇作为最终⽬标。

算法过程如下：1）从N个⽂档随机选取K个⽂档作为中⼼点；2）对剩余的每个⽂档测量其到每个中⼼点的距离，并把它归到最近的质⼼的类；3）重新计算已经得到的各个类的中⼼点；4）迭代2～3步直⾄新的质⼼与原质⼼相等或⼩于指定阈值，算法结束。

算法优缺点：优点：原理简单速度快对⼤数据集有⽐较好的伸缩性缺点：需要指定聚类数量K对异常值敏感对初始值敏感代码实现：⾸先我们随机⽣成200个点，就取（0,2000）之间的，并确定质⼼个数，这⾥就取个3个质⼼，也是随机⽣成（可以根据需求改变）如下：import randomimport matplotlib.pyplot as pltrandom_x = [random.randint(0,2000) for _ in range(200)]random_y = [random.randint(0,2000) for _ in range(200)]random_poinsts = [(x, y) for x, y in zip(random_x, random_y)]def generate_random_point(min_,max_):return random.randint(min_,max_),random.randint(min_,max_)k1,k2,k3 = generate_random_point(-100,100),generate_random_point(-100,100),generate_random_point(-100,100)plt.scatter(k1[0],k1[1],color = 'red',s=100)plt.scatter(k2[0],k2[1],color = 'blue',s=100)plt.scatter(k3[0],k3[1],color = 'green',s=100)plt.scatter(random_x,random_y)结果如下：接着导⼊numpy，来计算各个点与质⼼的距离，并根据每个点与质⼼的距离分类，与第⼀个点近则分配在列表的第⼀个位置，离第⼆个近则分配到第⼆个位置，以此类推，如下import numpy as npdef dis(p1,p2): #这⾥的p1,p2是⼀个列表[number1,number2] 距离计算return np.sqrt((p1[0] - p2[0])**2 + (p1[1]-p2[1])**2)random_poinsts = [(x, y) for x, y in zip(random_x, random_y)] #将100个随机点塞进列表groups = [[],[],[]] #100个点分成三类for p in random_poinsts: #k1,k2,k3是随机⽣成的三个点distances = [dis(p,k) for k in [k1,k2,k3]]min_index = np.argmin(distances)#取距离最近质⼼的下标groups[min_index].append(p)groups结果如下：[[(1000, 867),(1308, 840),(1999, 1598),(1606, 1289),(1324, 1044),(780, 923),(1915, 788),(443, 980),(687, 908),(1763, 1039),(1687, 1372),(1932, 1759),(1274, 739),(939, 1302),(790, 1169),(1776, 1572),(1637, 1042),....可以看到，这200个点根据与三个质⼼的距离远近不同，已经被分成了三类，此时groups⾥⾯有三个列表，这三个列表⾥分别是分配给三个质⼼的点的位置，接着我们将其可视化，并且加⼊循环来迭代以此找到相对最优的质点，代码如下：previous_kernels = [k1,k2,k3]circle_number = 10for n in range(circle_number):plt.close() #将之前的⽣成的图⽚关闭kernel_colors = ['red','yellow','green']new_kernels =[]plt.scatter(previous_kernels[0][0],previous_kernels[0][1],color = kernel_colors[0],s=200)plt.scatter(previous_kernels[1][0],previous_kernels[1][1],color = kernel_colors[1],s=200)plt.scatter(previous_kernels[2][0],previous_kernels[2][1],color = kernel_colors[2],s=200)groups = [[],[],[]] #100个点分成三类for p in random_poinsts: #k1,k2,k3是随机⽣成的三个点distances = [dis(p,k) for k in previous_kernels]min_index = np.argmin(distances)#取距离最近质⼼的下标groups[min_index].append(p)print('第{}次'.format(n+1))for i,g in enumerate(groups):g_x = [_x for _x,_y in g]g_y = [_y for _x,_y in g]n_k_x,n_k_y = np.mean(g_x),np.mean(g_y)new_kernels.append([n_k_x,n_k_y])print('三个点之前的质⼼和现在的质⼼距离：{}'.format(dis(previous_kernels[i],[n_k_x,n_k_y])))plt.scatter(g_x,g_y,color = kernel_colors[i])plt.scatter(n_k_x,n_k_y,color = kernel_colors[i],alpha= 0.5,s=200)previous_kernels = new_kernels结果如下：第1次三个点之前的质⼼和现在的质⼼距离：344.046783724601三个点之前的质⼼和现在的质⼼距离：178.67567512699137三个点之前的质⼼和现在的质⼼距离：85.51258602308063第2次三个点之前的质⼼和现在的质⼼距离：223.75162213961798三个点之前的质⼼和现在的质⼼距离：41.23571511332308三个点之前的质⼼和现在的质⼼距离：132.0752155320645第3次三个点之前的质⼼和现在的质⼼距离：87.82012730359548三个点之前的质⼼和现在的质⼼距离：22.289121504444285三个点之前的质⼼和现在的质⼼距离：33.55374236991017第4次三个点之前的质⼼和现在的质⼼距离：50.94506045880864三个点之前的质⼼和现在的质⼼距离：25.754704854433683三个点之前的质⼼和现在的质⼼距离：23.145028187286528第5次三个点之前的质⼼和现在的质⼼距离：66.35519842692533三个点之前的质⼼和现在的质⼼距离：31.90944410706013三个点之前的质⼼和现在的质⼼距离：36.247409926389686第6次三个点之前的质⼼和现在的质⼼距离：46.17069651194525三个点之前的质⼼和现在的质⼼距离：15.076857795406966三个点之前的质⼼和现在的质⼼距离：42.59620276776667第7次三个点之前的质⼼和现在的质⼼距离：36.7751709217284三个点之前的质⼼和现在的质⼼距离：15.873333735074496三个点之前的质⼼和现在的质⼼距离：23.469882661161705第8次三个点之前的质⼼和现在的质⼼距离：0.0三个点之前的质⼼和现在的质⼼距离：0.0三个点之前的质⼼和现在的质⼼距离：0.0第9次三个点之前的质⼼和现在的质⼼距离：0.0三个点之前的质⼼和现在的质⼼距离：0.0三个点之前的质⼼和现在的质⼼距离：0.0第10次三个点之前的质⼼和现在的质⼼距离：0.0三个点之前的质⼼和现在的质⼼距离：0.0三个点之前的质⼼和现在的质⼼距离：0.0这⾥设置了总共迭代10次，可以看到在迭代到第⼋次的时候就找到了最优的质点，如图所⽰：那么，以上就是对于k-means算法的⼀个简单实现，如果有任何问题，欢迎留⾔。