简单的二阶数独
- 格式:xls
- 大小:41.50 KB
- 文档页数:2
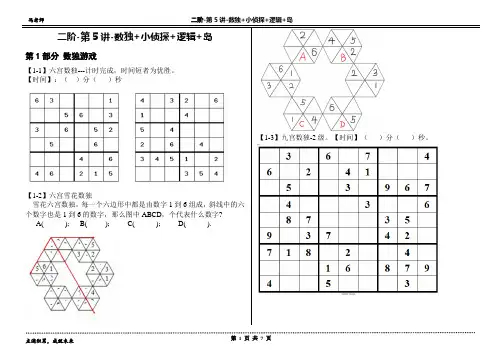
二阶-第5讲-数独+小侦探+逻辑+岛第1部分数独游戏【1-1】六宫数独---计时完成,时间短者为优胜。
【时间】:()分()秒【1-3】九宫数独-2级。
【时间】()分()秒。
【1-2】六宫雪花数独雪花六宫数独,每一个六边形中都是由数字1到6组成,斜线中的六个数字也是1到6的数字,那么图中ABCD,个代表什么数字?A( ); B( ); C( ); D( ).【3-2】横向思维一个人正在考察一座大山。
他的脚下突然一滑,跌倒了。
他滑倒的时候距离山顶还有150英尺,但是他滑倒后已经处于山顶了。
他没有攀登剩余的路程,也没有被同事们拉到山顶。
他是怎么滑到山顶的?【提示】1、他是在同一座山上,而且山顶就在他上面;2、他没有靠氢气球或者氦气球帮助;3、没有绳子也没有滑轮;4、没有上升的热气流;5、不是在看电影;【答案】【3-3】我的作业是对的幼儿园老师给孩子布置了一些数学计算题作为家庭作业。
第二天,老师把汤姆叫出去,并且告诉他所有的题目都做错了。
汤姆的答案排列如下图所示:汤姆的也没有错。
这是怎么回事呢?【答案】【3-4】逻辑数值--“?”号的地方数值是多少?【答案】【3-5】过桥问题--最短时间是多少?A、B、C、D、E、F六人晚上出行,速度分别为:1分、2分、3分、4分、5分、6分。
他们要经过一座桥,六人只有一把手电筒,桥上没有灯光,过桥必须要手电筒,并且每次只能两人一起过桥,然后其中一个人回来送手电筒,那么六人通过桥最少需要多少分钟?第4部分岛谜题岛主要锻炼什么能力?【推理力】解答岛谜题时,通常是从数字最小或者最大的第一个岛屿出发,根据已知条件,连接合理数量的桥梁到达第二个岛屿,再通过分析和整理其他已知条件,连续推理,不断引出新的桥梁到达新的岛屿。
以此反复,最终把所有的岛屿连成一个整体。
【专注力】【4-1】岛与桥【4-2】岛与桥----规则同上。
解谜之前,要快速分析谜题给出的已知条件,提炼有效信息,迅速找到切入点,更快、更有效地分析后续岛屿的信息,再根据这些信息做出初步的假设与判断。

以下我们将叙述一道标准数独的全部解题过程,在此过程中涉及到的技巧有摒除法、余数法、区块法、数对法、X- Wing这几个常在数独书籍中会涉及到的技巧,文中将描述各个技巧的结构及作用效果,相信在看完解题过程之后,您能相当程度地掌握到数独的基本解题技巧,也能在解题的过程中发现数独给您带来的乐趣。
谜题如下图第一招:摒除法大家之前已阅读过数独的规则:在每个单元中,每个数字只能出现一次,那么也就意味着,如果一行已经出现了一个1,这行的其他格就不再有1,利用这个观点,引发出摒除法。
第1步:数字2对B1进行摒除r1c8为2,则其所在R1不再有2;r2c4为2,则其所在R2不再有2;r9c2为2,则其所在C2不再有2,在B1中还没有2,B1有6个空格可以填2,但其中5个空格被摒除了,只剩下r3c1,所以得到第一解:r3c1=2这个方法因为是对宫实施摒除的,所以叫宫摒除法。
宫摒除法是解题技巧里面最简单的一种,也是解题过程中使用最多的一种。
其实解数独就是这么简单!第2步:r1c3=7(宫摒余解,数字7对B1摒除)第3步:r4c7=7(宫摒余解,数字7对B6摒除)第4步:数字7对C5进行摒除r1c3为7;则其所在R1不再有7;r2c9为7,则其所在R2不再有7;r4c7为7,则其所在R4不再有7;r6c2为7,则其所在R6不再有7;r8c1为7,则其所在R8不再有7;r9c8为7,则其所在R9不再有7,在C5中还没有7,C5有7个空格可以填7,但其中6个空格不能为7了,所以天元格r5c5=7这个方法因为是对列实施摒除的,所以叫列摒除法,与其类似的还有行摒除法。
行列摒除法也是很常用的方法。
见识了摒除法之后,大家是否尝试寻找另一个摒余解呢?不好意思要给大家泼凉水了,因为这个盘势下已经找不到宫摒余解或者行列摒余解了,那怎么办呢,没关系,我们继续介绍其它的技巧。
第二招:余数法前面我们提到,一格受其所在单元中其他20格的牵制,假如这20格里面已经出现了1-8这8个数字,我们就可以断定这格一定是未出现的唯一数字9。

数独入门及技巧9宫格全文共四篇示例,供读者参考第一篇示例:数独是一种益智游戏,源自日本,通过填入数字1-9在一个9x9的网格中,使每一行、每一列和每一个3x3的小方格中都包含数字1-9,且数字不重复。
数独看似简单,实际上需要一定的逻辑推理和技巧。
下面我们将介绍一些数独的入门知识和技巧,帮助您更好地解决数独难题。
第一步:了解数独规则第二步:找准切入点在解数独时,需要找准一个切入点,通常从一些已知数字比较多的行、列、小方格入手。
首先找出可确定的数字,填入网格中,然后逐步填入其他数字。
第三步:排除法在填字过程中,遇到疑难问题时,可以运用排除法。
在某个方格中,可能有几个数字都是可能的选择,可以通过推理和逻辑排除那些不可能的数字,从而确定正确的数字。
第四步:观察法观察法是解决数独问题的有效技巧之一。
通过观察每一行、每一列和每个小方格中已经存在的数字,来推断其他方格中应该填入的数字。
定位已知数字和求解未知数字之间的联系,是解决数独难题的关键。
第五步:尝试法在遇到难题时,可以尝试填入一些可能的数字,然后根据填入的数字继续遍历推断解题。
如果发现填入的数字有矛盾或者无解,就需要重新考虑填入的数字,并尝试其他可能的解决方法。
数独是一项耐心和逻辑的游戏,通过不断练习和探索,可以提高解决问题的能力。
希望上述数独入门及技巧可以帮助您更好地解决数独难题,提高数独游戏的乐趣和挑战性。
祝您解题愉快,享受数独的乐趣!第二篇示例:数独,又称“九宫格”,是一种风靡全球的数学逻辑游戏。
它的规则很简单,只需填入1至9的数字,保证每行、每列和每个九宫格内的数字都不重复即可。
虽然规则简单,但数独却是一款极具挑战性的益智游戏,需要玩家在排除多种可能性的灵活运用逻辑推理和专注力,才能完成每一道题目。
入门技巧:1. 专注观察:数独游戏的第一步是观察。
仔细观察整个数独盘面,找出已知数字的位置,并根据它们的位置和限制条件,推断其他数字的可能位置。
2. 逻辑推理:数独的一个核心技巧就是逻辑推理。


数独技巧_数独的进阶方法介绍(2)数独历史发展起源既然“数独”有一个字是“数”,人们也往往会联想到数学,那就不妨从大家都知道的数学家欧拉说起,但凡想了解数独历史的玩家在网络、书籍中搜索时,共同会提到的就是欧拉的“拉丁方块(Latin square)”。
拉丁方块的规则:每一行(Row)、每一列(Column)均含1-N(N即盘面的规格),不重复。
这与前面提到的标准数独非常相似,但少了一个宫的规则。
近代发展数独起源于18世纪初瑞士数学家欧拉等人研究的拉丁方阵(Latin Square)。
19世纪80年代,一位美国的退休建筑师格昂斯(Howard Garns)根据这种拉丁方阵发明了一种填数趣味游戏,这就是数独的雏形。
20世纪70年代,人们在美国纽约的一本益智杂志《Math Puzzles and Logic Problems》上发现了这个游戏,当时被称为填数字(Number Place),这也是目前公认的数独最早的见报版本。
1984年一位日本学者将其介绍到了日本,发表在Nikoli公司的一本游戏杂志上,当时起名为“Suuji wa dokushin ni kagiru”,就改名为“sudoku”,其中“su”是数字的意思,“doku”是单一的意思。
后来一位前任香港高等法院的新西兰籍法官高乐德(Wayne Gould)在1997年3月到日本东京旅游时,无意中发现了。
他首先在英国的《泰晤士报》上发表,不久其他报纸也发表,很快便风靡全英国,之后他用了6年时间编写了电脑程式,并将它放在网站上(这个网站也就是著名的数独玩家论坛),后来因一些原因,网站被关闭,幸好数独大师Glenn Fowler恢复了数据,玩家论坛有了新处所。
在90年代国内就有部分的益智类书籍开始刊登,南海出版社在2005年出版了《数独1-2》,随后日本著名数独制题人西尾彻也的《数独挑战》也由辽宁教育出版社出版。
《北京晚报》、《扬子晚报》、《羊城晚报》、《新民晚报》、《成都商报》等等报纸媒体也先后刊登了数独游戏。


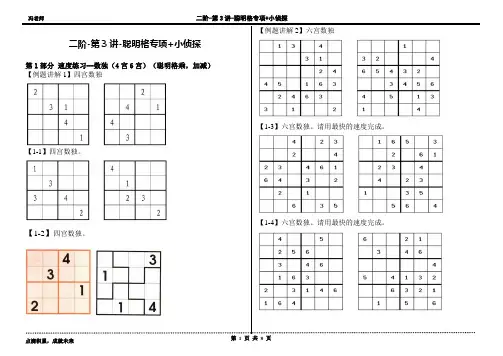
二阶-第3讲-聪明格专项+小侦探第1部分速度练习--数独(4宫6宫)(聪明格乘,加减)【例题讲解1】四宫数独【1-1】四宫数独。
【1-2】四宫数独。
【例题讲解2】六宫数独【1-3】六宫数独。
请用最快的速度完成。
【1-4】六宫数独。
请用最快的速度完成。
【小侦探1】破绽在哪里?B公司的董事长办公室里发生了一起命案。
董事长吴先生被杀害,死因是刀子刺穿心脏,这件案子没有告诉任何百姓和员工,只有警方知道。
要是公布开就会有不安定的因素。
警方请来了死者的妻子。
下面是他们的对话:警察说:“您的丈夫被人杀害了”。
死者的妻子非常痛苦,不停的在哭。
妻子说:“不可能,他又没得罪什么人,他怎么会被刀子刺死了呢?”警察说:“好了,凶手就是你,死者的妻子!”警官是怎么知道凶手就是死者的妻子呢?【答案】【例题讲解3】聪明格数独-----三宫乘法。
规则:1、每行只有数字1、2、3这三个数字;每行不可以重复出现;2、左上角的数字和符号表示粗线分成的格子内数字相乘的积;3、单格直接将数字写在格子内;【1-5】四宫乘法数独---规则:----如图(1-5)1、每行只有数字1、2、3、4这四个数字;每行不可以重复出现;2、左上角的数字和符号表示粗线分成的格子内数字相乘的积;3、单格直接将数字写在格子内;【1-6】四宫、四则混合数独---规则:如图(1-6)1、在方格中分别填入1~4的数字。
2、每一行,每一列都要分别填入1~4的数字。
3、左上角的数字和+、-、×、÷符号分别粗框内所填数字之和、差、积、商。
4、左上角只有1个数字(无运算符号)时,就将该数字填入此方格中。
【小侦探2】关键线索-5秒钟断案一天上午,杰克和约翰去看望住在郊区别墅的金姆森太太。
平常他们要进去都要按门铃,今天的门却是虚掩着的。
杰克和约翰推开门进去,在一楼餐厅里发现了金姆森太太的尸体,看上去,她已经遇害十多天了。
她是在用餐的时候遭到突然袭击的,一柄尖刀贯穿胸口,瞬间夺去了她的生命。


味数学 QUWEISHUXUE数海星空神奇fi925Bft 数独幻方♦方有昆数独幻方是数独和幻方的有效结合,利用珠心算 功能,来研究和探索数字科学领域中的神奇奥秘,使此 幻方品位和境界得到了进一步提升,正所谓:数字世 界、奥妙无穷。
此幻方好似天上的星星布满天空,相互 依存,相互依赖,令人赏心悦目,变幻莫测。
特性如下:1. 每行1至25个数字不重复,和都等于325 ;2. 每列1至25个数字不重复,和都等于325 ;3. 毎条对角线1至25个数字不重复,和都等于325;4. 每个粗实线内5x5方阵,1至25个数字不重复,和都 等于325;5. 每个粗实线内5x5方阵中有25个格子,在每个方 阵的25格中,各取一个相同位置的数,1至25个数字不重复,和都等于325;6. 其他有规律的组合,1至25个数字不重复,和都等于325;7. 将第一行1至25的数变化排列,以表中介绍的方法,无论是A 图还是B 图都可以编排出1.5亿亿亿(25的 阶乘)组相同品位和境界的数独幻方。
&最大的亮点是:A 、B 两个图相互对应关联,如A 图中每个粗实线5x5方阵中,同数的25个位置,其25个 位置在B 图中就是不重复的1至25个数,数字之和都为325;反之B 图中每个粗实线5x5方阵中,同数的25个位 置,其25个位置在A 图中也是不重复的1至25个数,数字 之和都为325;如A 图中数字8的25位置,在B 图中就是1~ 25二十五个数,其数字之和都等于325;反之B 图中数字 8的25个位置,在A 图中就是1~25二十五个数,其数字之和都等于325;以此类推其它24个数也同样如此。
备注:1. 数字可以转变为英文字母、颜色、地名、姓氏等,来提高趣味性;2. 以此方法,可以编排出2阶多品位和高境界的数独幻方。
实验及珠算竞赛基础上,珠算内化形成的“珠心算”得 到了普及。
珠心算是珠算的升华,通俗讲“珠心算就是在脑子里打算盘”,较为严谨的说法,珠心算就是将算 盘和珠算的运算模型内化于大脑,形成珠像,脑中操作珠像而实现的运算。

数独的高阶解法1. 引言数独是一种经典的逻辑游戏,通过填写数字来完成一个9x9的方格。
每个方格中只能填写1到9的数字,且同一行、同一列和同一个小九宫格内不能有重复数字。
在初级解法基础上,数独还有一些高阶解法技巧,可以帮助玩家更快地解决难题。
本文将介绍数独的高阶解法技巧,包括候选数法、唯余法、剑鱼等。
这些技巧可以让你在面对更复杂的数独问题时更加游刃有余。
2. 候选数法候选数法是一种基本的高级解法技巧。
在某些情况下,我们无法确定某个格子应该填写哪个数字。
这时,我们可以先在该格子中标记所有可能的候选数字,然后通过推理和排除来确定正确答案。
例如,在某个格子中有两个候选数字2和5,但我们无法确定具体应该填写哪个数字。
那么我们可以将该格子标记为(2,5)。
当其他相关区域(行、列、小九宫格)已经确定了某些数字后,我们可以根据已知数字的位置来排除一些候选数字。
最终,通过不断的推理和排除,我们可以确定该格子的正确答案。
3. 唯余法唯余法是一种高效的解题技巧,通过找到某个区域(行、列、小九宫格)中唯一一个可能填写某个数字的格子来解题。
例如,在某行中只有一个格子可以填写数字7,那么我们就可以确定该格子应该填写7。
同样地,在某列或小九宫格中也可以使用唯余法来确定某个格子的答案。
唯余法是数独解题过程中常用的技巧之一,尤其在难度较低的数独问题中非常有效。
4. 剑鱼剑鱼是一种高级解题技巧,通过找到多个候选数字组成特定形态来解题。
具体而言,当某行或某列中有三个格子只能填写三个特定的数字,并且这些数字在其他行或其他列没有出现时,我们就可以应用剑鱼技巧。
通过排除其他行或其他列中与这三个特定数字相关联的候选数字,我们可以确定这三个特定数字所在行或所在列中相应位置上的答案。
剑鱼是数独解题中较为复杂的技巧,需要一定的经验和观察力来运用。
5. 总结数独的高阶解法技巧包括候选数法、唯余法和剑鱼等。
这些技巧可以帮助玩家更快地解决难题,提高解题效率。
数独策略解密最有效的方法数独是一种非常受欢迎的逻辑推理游戏,它的规则简单而又富有挑战性。
在解答数独谜题的过程中,我们常常需要运用一系列策略来帮助我们揭开谜底。
本文将介绍一些最有效的数独策略,让你能够更好地解密数独。
【基础策略】在解密数独之前,我们首先需要掌握一些基础策略。
这些策略更加侧重于观察并填写已知的数字,以便为后续推理提供基础。
1. 唯一候选数法:当一个空格的可能数字只有一个的时候,那么该数字就是该空格的解答。
通过观察其他行、列和九宫格中已经填入的数字,我们可以确定一个数字在某个空格的唯一性。
2. 排除法:在每一行、每一列以及每一个九宫格中,如果某个数字已经在该行、该列或该九宫格中出现过,那么该数字就不能出现在该行、该列或该九宫格的其他空格。
通过排除一些已知的数字,我们可以缩小其他空格的候选数字范围。
【进阶策略】除了基础策略之外,还有一些进阶策略可以帮助我们解密更加复杂的数独谜题。
这些策略需要更多的逻辑思考和观察能力。
1. 唯余法:当某个数字在某行、某列或某九宫格中只剩下一个空格可填时,该空格必然是该数字的解答。
在解密数独过程中,我们需要仔细观察每行、每列和每个九宫格中数字的分布情况,判断出哪些数字的唯余空格可以确定。
2. 隐性唯余法:当一个数字在某行、某列或某九宫格中只有一个位置可填时,即使该位置有多个候选数,也可以确定该数字就是要填入的数。
这是因为其他空格上的候选数会被其他规则所排除。
3. X-Wing法:当某个数字在两行或两列中只出现两次,且这两个位置满足特定条件时,可以排除其他行或列上相同位置的该数字。
X-Wing法需要观察不同行和列中数字的分布情况,找到特定形态的重复数字并进行排除。
4. 锁定候选数法:当一个数字在某行或某列中只出现在一个九宫格的两个空格中,可以排除该九宫格中其他行或其他列上相同位置的该数字。
锁定候选数法需要观察不同行和列中数字的分布情况,找到特定形态的数字分布以及包含候选数字的九宫格。
数独困难级别题目
数独是一种逻辑游戏,其目标是在9x9的格子中填入数字1-9,使得每一行、每一列以及每一个3x3的小格子中都包含这9个数字,且不能重复。
难度级别取决于题目的复杂程度和解决它所需的时间和努力。
数独困难级别的题目通常具有以下特点:
1.高难度初始条件:有些数独题目一开始就有很多限制,使得解题步骤大大减少,从而增加了难度。
例如,一些题目可能已经有了几个数字,或者某些行或列已经有了完整的数字。
2.高密度:一个题目中有很多需要填入的数字,或者某些数字在多个位置都适用,这需要玩家仔细考虑如何填入数字,以避免出现矛盾。
3.多个解决方案:一个数独题目可以有多个解决方案,这需要玩家在解决过程中始终保持警觉,以免错过其他可能的解决方案。
4.高阶数独:除了标准的9x9数独外,还有更大的数独版本,如16x16、25x25等,这需要玩家具备更高的逻辑推理能力才能解决。
5.异形数独:这种数独的形状不是方形的,例如三角形、六边形、圆形等,这使得解题的规则和策略都有所不同。
6.其他限制条件:有些数独题目会有额外的限制条件,例如某些数字只能在特定的行或列中出现,或者某些数字不能出现在某些位置等。
为了提高解决数独题目的能力,玩家可以尝试不同类型的数独题目,学习并掌握各种解题技巧和策略。
五六数独训练题目如下:
题目一:
1. 9 3 5 7 8 4 6 2 1
2. 6 7 4 9 5 3 8 5 3
3. 5 8 2 1 6 9 4 7 6
4. 8 1 6 2 4 5 9 3 7
5. 7 9 3 4 8 2 5 1 6
6. 2 4 1 5 3 7 6 9 8
7. 3 2 9 7 6 8 1 4 X
8. X X X X X X X X X X
题目二:
1. 进行一次随机的六阶数独。
2. 对初学者提供五个问题。
这些问题在简单难度下可能会导致迷惑。
确保答案清晰明确。
3. 一份三阶数独解答样例。
让训练者观察解答过程中的策略使用,尤其是他们可能在多阶段解决中遇到的问题。
题目三:
1. 在一个六宫数独中,设置一些挑战性的问题,这些问题可能需要训练者使用一些高级策略,如假设验证或行/列/宫的连续检查。
2. 提供一份难度适中的六阶数独,并要求训练者找到所有的空单元格并标记它们。
然后给出正确的填充方案。
3. 对于一些熟练的训练者,提供一个复杂的三阶数独,并鼓励他们寻找解决此类问题的方法和策略。
以上就是一些五六数独训练题目,具体的答案和解答思路可能需要您自行探索和研究。
数独是一种逻辑游戏,需要耐心和细心,希望这些题目可以帮助您提高数独技能。
需要注意的是,这些题目主要是为了训练和提升数独技能,难度和问题设置都是为了适应不同水平的玩家。
在解答这些题目时,需要充分理解题目要求,仔细分析数字和空格分布,运用逻辑和推理,逐步解决问题。
同时,也可以参考一些数独的规则和技巧,以提高解题效率。
数独解法七种解法:媒介数独这个数字解谜游戏,完整不须要用到算术!会用到的只是推理与逻辑.刚开端接触数独时,即使是只须用到"独一解"技能的简略单纯级谜题,就已可让我们焦头烂额了,但是跟着我们深陷数独的迷人世界之后,这类简略单纯级的数独谜题确定在短时光内难再使我们获得驯服的知足.于是,当我们慢慢深刻.进阶到更难的游戏后,我们将会须要成长龈?多的解谜技能.固然最好的技能等于我们本身发明的窍门,如许我们很轻易??能记住它们,应用自如,不须要他人来耳提面命.但是假如完整不去不雅摩进修他人成长出来的技能,而端赖本身探索,那将是一个异常坚苦的挑衅,也不是准确的进修之道!所以让我们一齐来商量数独的解谜办法吧!数独的解谜技能,刚开端成长时,以直不雅式的独一解及摒除法为主,对于初入门的玩家来说,这也是一般人较轻易懂得.接收的办法,对于一般简略单纯级或中级的数独谜题,假如能灵巧应用此二轨则,平日已游刃有余.1.独一解法当数独谜题中的某一个宫格因为所处的列.行或九宫格已消失过的数字已达8 个,那么这个宫格所能填入的数字就剩下这个还没消失过的数字了.<图 1> (9, 8)消失独一解了<图1>是最显著的独一解消失机会,请看第8 行,由(1,8) ~(8,8) 都已填入数字了,只剩(9,8)照样空白,此时(9,8)中应填入的数字,当然就是第 8 行中还没消失过的数字了!请一个个数字查对一下, 哦!是数字8 还没消失过,所以(9,8) 中该填入的数字就是数字8了.<图 2> (8, 9)消失独一解了<图 2>是另一个显著消失独一解的情况,请看第 8 列,由 (8,1) ~(8,8) 都已填入数字了,只剩(8,9)照样空白,此时(8, 9)中应填入的数字,当然就是第8 列中还没消失过的数字了!请一个个数字查对一下, 哦!是数字9 还没消失过,所以(8, 9) 中该填入的数字就是数字9 了.<图 3> (7, 5)消失独一解了<图 3>是另一种显著消失独一解的情况,请看下中九宫格,在这个九宫格中除了(7, 5)照样空白外,其他宫格都已填稀有字了,所以(7, 5)中应填入的数字,当然就是下中九宫格中还没消失过的数字了!请一个个数字查对一下, 哦!是数字 1 还没消失过,所以(7, 5) 中该填入的数字就是数字 1 了.<图 4> 一般情况下的独一解相似<图1>~<图3>这种显著消失独一解的情况,在一般情况之下及解题初期是不太可能消失的!<图4>是一个最典范的简略单纯级数独谜题,假如单纯不雅察某一个行.列或九宫格,没有一处是已消失8 个数字的, 岂非如斯就无解了吗?非也!非也!在此图中,消失独一解的宫格其实有 3 处之多!你能找出来吗?没错,在一般情况之下及解题初期,独一解的查找必须分解所处的行.列及九宫格三者,同时过滤筛选出已消失的数字才行!假如漏掉落其一,可能就无法找出独一解的消失地位了.如今且不忙着填入数字,先来找找看<图 4>中今朝已消失的独一解在哪儿吧:第一个独一解地位在(2, 3):(2, 3) 所处的第2 列中已消失的数字是:9.3.5.7.所处的第3 行中已消失的数字是:4.2.6.8.至于所处的上左九宫格中,已消失的数字是:2.9.4.所以分解而言, 受其所处地位的行.列及九宫格影响,不得再应用并填入(2, 3) 的数字计有:2.3.4.5.6.7.8.9. 能用来填入的数字确切只剩数字 1 这个独一的解了.第二个独一解地位在(8, 7):(8, 7) 所处的第8 列中已消失的数字是:1.2.8.6.所处的第7 行中已消失的数字是:3.9.5.4.至于所处的下右九宫格中,已消失的数字是:4.6.5.所以分解而言, 受其所处地位的行.列及九宫格影响,不得再应用并填入(8, 7) 的数字计有:1.2.3.4.5.6.8.9. 能用来填入的数字确切只剩数字 7 这个独一的解了.第三个独一解地位在(5, 5):(5, 5) 所处的第 5 列中已消失的数字是:1.7.所处的第 5 行中已消失的数字是:2.5.至于所处的中心九宫格中,已消失的数字是:3.6.8.9.所以分解而言, 受其所处地位的行.列及九宫格影响,不得再应用并填入(5, 5) 的数字计有:1.2.3.5.6.7.8.9. 能用来填入的数字确切只剩数字 4 这个独一的解了.以上所谓的三个独一解地位,是以<图4>现况未填入任何数字之前而言,假如开端填入数字,消失独一解的地位可能将随之增长.例:当(8, 7) 填入数字 7 之后,(7, 7)将消失独一解 1;假如再将数字 1 填入(7, 7), 在(7, 8)又将消失独一解 3;......如斯不竭轮回下去,就可以将全部谜题解出了.2.独一候选数法概说按照候选数法概说一文中,候选数表的制造规矩,我们可以知道:可以填入某一个宫格的数字,必定会列于该宫格的候选数中;不在候选数中的数字,就不克不及填入该宫格中.所以假如在候选数表中发明某一个宫格的候选数仅有1 个数字,那就是暗示:不必再斟酌了!这个宫格就是只能填入这个数字啦!假如填入此外数字,就会违背数独的填制规矩的.应用“找出候选数表中,候选数仅有1 个数字的宫格来,并填入该候选数”的办法就叫做独一候选数法(Singles Candidature, sole Candidate).独一候选数法示例<图 1>数独谜题的候选数表<图 1> 是我们在候选数法概说一文中完成的候选数表,个中有好几个宫格的候选数都只有1 个,所以可以应用独一候选数法来进行填制.先还不要填入数字,我们先来找找看,有哪些宫格有独一候选数?在 (2, 7) 有独一候选数 7.在 (5, 5) 有独一候选数 5.在 (8, 3) 有独一候选数 3.哇!同时消失了3 个独一候选数啊!那么,先填入哪一个会不会影响填制成果呢?当然不会了, 只要你愉快,爱好先填哪一个都没问题的.好,就在这 3 个宫格中填入他们的独一候选数吧,填制成果如<图2>:<图 2>哇!又有独一候选数消失了呢!没错,一般简略单纯级的数独谜题,假如应用直不雅式的独一解法及摒除法来解题,即使是数独熟手在行,也要消费相当的功夫才干完成; 但是假如采取独一候选数法,从候选数表制造完成开端,独一候选数将一个一个接连不竭的消失,轻轻松松的就可以完成解题啦!<图3> 是<图1> 的完成解.<图 3>完成解3.隐性三链数删减法概说碰到了高等.艰苦级的数独谜题,使得独一候选数法和隐性独一候选数法黔驴之技的时刻,就是各类删减法上场的机会了.在各类的删减法中,哪一个要先用是随小我之爱好的,并没有限制.本页介绍的例子当然可用其他删减法完成解题,但照样要以隐性三链数删减法优先??!<图 1>请看<图 1>的第 2 列,数字 1.7.8 只出如今(2, 1).(2, 7)和(2, 8)这三个宫格的候选数中;这时隐性三链数删减法的前提已成立了!这暗示第 2 列的数字 1.7 和 8 将只能填到这三个宫格中,因为:假如让此外数字填入这三个宫格之中后,这三个相异的数字能填入的可能宫格就只剩下两个,而那是不成能的事!所以若这三个宫格的候选数中还有其他数字,全体是过剩无用的,它们已不成能再用来填入这些宫格中了,所以可以毫不斟酌的把它们删减掉落.于是(2, 7)和(2, 8)这两个宫格候选数中的 6 都可被安然的删减掉落;个中(2, 7)的候选数少了数字 6,将使得(8, 7)消失行隐性独一候选数 6 ,于是可用隐性独一候选数法来填入下一个解了.整顿一下:当某3 个数字仅出如今某列的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该 3 个数字.同理,当某 3 个数字仅出如今某行的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该 3 个数字.当然,当某 3 个数字仅出如今某个九宫格的某三个宫格候选数中时,就可以把这三个宫格的候选数删减成该3 个数字.应用“找出某3 个数字仅出如今某行.某列或某一个九宫格的某三个宫格候选数中的情况,进而将这三个宫格的候选数删减成该3 个数字”的办法就叫做隐性三链数删减法(Hidden Triples).本法其实为隐性数对删除法的推广,并且还可以持续加以推广:隐性四链数删减法就是:“找出某4 个数字仅出如今某行.某列或某一个九宫格的某四个宫格候选数中的情况,进而将这四个宫格的候选数删减成该4 个数字”的办法.隐性五链数删减法就是:“找出某 5 个数字仅出如今某行.某列或某一个九宫格的某五个宫格候选数中的情况,进而将这五个宫格的候选数删减成该 5 个数字”的办法.......假如同意的话,你确切是可以如许推广的,只是,适用上是否有其应用的价值或空间呢?隐性三链数删减法示例隐性三链数删减法一共有3 种状态:第一种产生在行.第二种是产生在列.第三种则产生在九宫格.<图 1> 就是产生在列的例子了,其他的情况举例如下:<图 2><图2> 是隐性三链数删减产生在行的例子:图中第 4 行的数字2.4.9 只出如今(4,4).(5, 4)及(6, 4) 这三个宫格的候选数中,所以可以将三个宫格候选数中2.4.9 以外的数字安然的删减掉落,(4, 4)的候选数删减成2.4; (5, 4)的候选数删减成2.4.9;(6, 4)的候选数删减成 9;消失了独一候选数啦!<图 3><图 3> 是隐性三链数删减产生在九宫格的例子:图中中心九宫格的数字 2.5.9 只出如今(5, 4).(5, 6)及(6, 4) 这三个宫格的候选数中,所以可以将三个宫格候选数中 2.5.9 以外的数字安然的删减掉落, (5, 4)的候选数删减成2.5.9;(5, 6)的候选数删减成2.5;(6, 4)的候选数删减成9;消失了独一候选数啦!<图 4>像 <图 1>~<图 3> 如许只经一次删减就消失下一个解的情况当然不错了,但有时可没法如许顺心, <图 4> 就是一个例子.下一个解将出如今(5, 6) 这个宫格,你能找出该填入什么数字吗?以今朝所学到的办法,要解出下一个解,须要二个步调:先看中左九宫格吧!因为只剩(5, 1)~(5, 3)这个区块尚未填入数字,所以可用区块删减法将第 5 列其他区块候选数中的 1.3.4 全体删减掉落,但现实上仅能删到(5, 4)及(5, 6)候选数的数字 4 罢了.接下来请不雅察第 6 行!因为数字 1.4.9 只出如今 (2, 6).(8, 6)及(9, 6) 这三个宫格的候选数中 [因为(5, 6)的候选数在上一步调中已被删减为5.8 了 ], 所以可用隐性三链数删减将三个宫格候选数中 1.4.9 以外的数字安然的删减掉落, (2, 6)的候选数删减成1.4.9;(9, 6)的候选数没变;(8, 6)的候选数则由 2.4.5.8.9 删减成 4.9; 因为 5 被删减掉落了,使得(5, 6) 消失了行隐性独一候选数5啦!4.隐性数对删减法概说碰到了高等.艰苦级的数独谜题,使得独一候选数法和隐性独一候选数法黔驴之技的时刻,就是各类删减法上场的机会了.在各类的删减法中,哪一个要先用是随小我之爱好的,并没有限制.本页介绍的当然就要以隐性数对删减法优先??!<图 1>请看<图1>的上右九宫格,数字8.9 都只出如今(2, 8)和(2, 9)这两个宫格的候选数中;这时隐性数对删减法的前提已成立了!这暗示上右九宫格的数字 8 和 9 将只能填到这两个宫格中,并且:假如数字 8 将填入(2, 8), 那么(2, 9)就必定要填入数字 9;反之,假如数字 9 将填入(2, 8),那么(2, 9)就必定要填入数字8; 不管哪一个状态消失,(2, 8)和(2, 9)这两个宫格的候选数中若还有其他数字,全体是过剩无用的,因为这两个宫格若填入数字 8.9 以外的数字,那么上右九宫格的数字 8 或 9 就将无处可填了.候选数的意义是可能填入该宫格的数字,而这两个数字以外的数字已不成能再用来填入本宫格中了,所以可以毫不斟酌的把它们删减掉落.当(2, 8)和(2, 9)这两个宫格的候选数都安然的删减成数字 8.9 之后,(2, 5)消失了列隐性独一候选数2 ,于是可用隐性独一候选数法来填入下一个解了.整顿一下:当某个数对仅出如今某个九宫格的某两个宫格候选数中时,就可以把这两个宫格的候选数删减成该数对.同理,当某个数对仅出如今某列的某两个宫格候选数中时,就可以把这两个宫格的候选数删减成该数对.当然,当某个数对仅出如今某行的某两个宫格候选数中时,就可以把这两个宫格的候选数删减成该数对.应用“找出某个数对仅出如今某行.某列或某一个九宫格的某两个宫格候选数中的情况,进而将这两个宫格的候选数删减成该数对”的办法就叫做隐性数对删减法(Hidden Pairs).当隐性数对删减法完成后,平日还可激发数对删减法;以<图1>为例,当(2, 8)和(2, 9)这两个宫格的候选数都安然的删减成数字 8.9 之后,还可应用数对删减法把 (2, 1).(2, 2).(2, 3) 这三个c格候选数中的数字 8 删减掉落.隐性数对删减法示例隐性数对删减法一共有3 种状态:第一种产生在行.第二种是产生在列.第三种则产生在九宫格.<图 1> 就是产生在九宫格的例子了,其他的情况举例如下:<图 2><图 2> 是隐性数对删减产生在行的例子:图中第 2 行的数对 4.6 只出如今 (3, 2)及(9, 2) 这两个宫格的候选数中,所以可以将(3, 2)及(9, 2)的候选数安然的删减成数对4.6;而经此一删,(3, 3) 宫格消失了列隐性独一候选数 1 啦!<图 3><图 3> 是隐性数对删减产生在列的例子:图中第 7 列的数对 4.7 只出如今 (7, 1)及(7,8) 这两个宫格的候选数中,所以可以将(7, 1)及(7, 8)的候选数安然的删减成数对4.7;而经此一删,(8, 1) 宫格消失了行隐性独一候选数 2 啦!三链列删减法概说碰到了高等.艰苦级的数独谜题,使得独一候选数法和隐性独一候选数法黔驴之技的时刻,就是各类删减法上场的机会了.在各类的删减法中,哪一个要先用是随小我之爱好的,并没有限制.本页介绍的例子当然可用其他删减法完成解题,且本删减法成立的前提和其他办法比拟稍嫌复杂,但为了介绍,在进行解题时照样要以三链列删减法优先??!<图 1>请看<图 1>第 1.4.6 列的数字 5 ,都只出如今第 1.5.8 行的宫格候选数中;这时三链列删减法的前提已成立了!这暗示第 1 行.第 5 行及第 8 行的数字 5 将只能被填到第 1 .4.6 列了,因为:第 1 列的数字 5 只出如今(1, 1)及(1, 8),所以数字 5 只能填到这两个宫格;先假设第 1 列的数字 5 将被填到(1, 1),第 1 行就不克不及再填数字 5 了,所以第 4 列的数字 5 只好填到(4, 5),第 6 列的数字 5 只好填到(6, 8);别的,假设第 1 列的数字 5 将被填到(1, 8),第 8 行就不克不及再填数字 5 了,所以第 6 列的数字 5 只好填到(6, 1)或(6, 5);假如第 6 列的数字 5 填到(6, 1),第 4 列的数字 5 就要填到(4, 5);假如第 6 列的数字 5 填到(6, 5),第 4列的数字 5 就要填到(4, 1);不管哪一种情况产生,第 1.5.8 行的数字 5 必定要填在第 1.4.6 列的交点,此外宫格已不克不及再应用数字 5 来填入了,所以若其他宫格的候选数中还稀有字 5,全体是过剩无用的, 可以毫不斟酌的把它们删减掉落.于是(5, 1).(5, 5).(9, 5)和(1, 8).(2, 8)这五个宫格候选数中的5 都可被安然的删减掉落;个中(9, 5)的候选数少了数字5,将使得(9, 4)消失列隐性独一候选数 5 ,于是可用隐性独一候选数法来填入下一个解了.整顿一下:当某个数字在某三列仅出如今雷同的三行时,就可以把这三行其他宫格候选数中的该数字删减掉落.同理,当某个数字在某三行仅出如今雷同的三列时,就可以把这三列其他宫格候选数中的该数字删减掉落.应用“找出某个数字在某三列仅出如今雷同三行的情况,进而将该数字自这三行其他宫格候选数中删减掉落”; 或“找出某个数字在某三行仅出如今雷同三列的情况,进而将该数字自这三列其他宫格候选数中删减掉落”的办法就叫做三链列删减法(Swordfish).本删减法其实是矩形极点删减法的推广,假如你同意的话,还可以持续推广:四链列删减法:应用“找出某个数字在某四列仅出如今雷同四行的情况,进而将该数字自这四行其他宫格候选数中删减掉落”;或“找出某个数字在某四行仅出如今雷同四列的情况,进而将该数字自这四列其他宫格候选数中删减掉落”的办法五链列删减法:应用“找出某个数字在某五列仅出如今雷同五行的情况,进而将该数字自这五行其他宫格候选数中删减掉落”;或“找出某个数字在某五行仅出如今雷同五列的情况,进而将该数字自这五列其他宫格候选数中删减掉落”的办法六链列删减法:...... 不过假如真的如许做,现实应用时,可以或许用上的机率精确不久不多就是了.碰到了高等.艰苦级的数独谜题,使得独一候选数法和隐性独一候选数法黔驴之技的时刻,固然你可以优先应用三链列删减法来查找下一个解;但大部分的人在应用删减法的优先次序上,平日都邑将三链列删减法排在稍后一点,为什么要如斯安插,在现实应用一段时光之后, 信任你自能领会了,但这个办法又是不成或缺的,假如不会应用本删减法,有许多高等的数独谜题就将无解了.三链列删减法示例三链列删减法只有 2 种状态:第一种的删减产生在行.第二种的删减产生在列.<图 1> 就是删减产生在行的例子了,第二种的情况举例如下:<图 2><图 2> 是三链列删减产生在列的例子:图中第 3.5.8 行的数字 2 只出如今第 3.4.5 列, 所以可以将数字 2 自(4, 6).(5, 6)的候选数中安然的删减掉落,个中(5, 6) 的候选数由 2.5 删减成 5 时,消失独一候选数啦!5.区块删减法概说碰到了高等.艰苦级的数独谜题时,独一候选数法和隐性独一候选数法仍有其黔驴之技的时刻;这时就是区块删减法上场的机会了,往后将要介绍的数对删减法(Naked Pairs).隐性数对删减法(Hidden Pairs).三链数删减法(Naked Triples). 隐性三链数删减法(Hidden Triples) .矩形极点删减法(X-Wing).三链列删减法(Swordfish)都具有相似的特征:应用这些技能的目标仅在删减候选数的数量,删减之后,照样得应用独一候选数法和隐性独一候选数法来找出下一个解并填入数字的.当应用独一候选数法或隐性独一候选数法找不出下一个解时,到底该先应用哪一个删减法呢?随您愉快的用吧!假如你比较善于应用数对删减法,那就先用数对删减法吧!假如你以为区块删减法比较好用,那就先用数对删减法吧! ......;介绍时总有先后的次序,但其实不暗示先介绍的就较好用或必须先用哦!只要能达到:“安然删减掉落候选数, 并找出下一个解”的目标,应用哪一种删减法都是可以的.<图 1>请看<图1>,这时若应用独一候选数法或隐性独一候选数法是找不出下一个解来的!就先来尝尝区块删减法吧. 请不雅察第 9 行:数字 1 在本行各宫格的候选数中,是不是仅出如今(1,9)~(3,9)的这一个区块中?太好了,区块删减的前提已有了;因为这暗示第9 行的数字1 只能填在(1,9)~(3,9)的这一个区块中,而不管填在本区块的哪一个宫格中,上右九宫格的其他宫格将因本九宫格已消失数字1,而不得再填入1,不然就违背数独填制的规矩啦!所以(1, 7)~(3, 7)及(1, 8)~(3, 8)这两个区块的宫格,假如其候选数中包含稀有字1,就可以毫不斟酌的把它删除掉落,因为候选数的意义是可能填入该宫格的数字,而这个数字已不成能再用来填入该宫格中了.啊!太好啦!(1, 7)的候选数中包含稀有字1,所以可以把(1, 7) 的候选数由1.6 删减成 6,于是可用独一候选数法来填入下一个解了.当区块删减法的前提成立时,可别愉快得太早,因为很有可能找不到可删减的数字,例如:在<图 1>的第 1 行中, 数字 2 在本行的各宫格候选数中,仅出如今(4, 1)~(6, 1)这一个区块中,而不管数字 2 未来会被填到本区块的哪一个宫格中,将使得数字 2 不得再填入(4, 2)~(6, 2)及(4, 3)~(6, 3)这两个区块中;但请找找看!这两个区块各宫格的候选数中全体没稀有字2,所所以白忙了一场,前提是成立了,但候选数并未是以而得到删减.整顿一下,并为了简化论述起见,下面所述的“区块候选数”暗示:该区块的各个宫格候选数的总和.例如(1, 3)~(3, 3) 的区块候选数就是(1, 3)的候选数 4.6.7 及(2, 3)的候选数 3.4.6 及(3, 3)的候选数 3.7 的总和: 3.4.6.7 啦!:当某一个数字只出如今某行的某一个区块候选数中时,就可以把该数字自包含该区块的九宫格之其他区块候选数中删减掉落.同理,当某一个数字只出如今某列的某一个区块候选数中时,就可以把该数字自包含该区块的九宫格之其他区块候选数中删减掉落.同理,当某一个数字只出如今某个九宫格的某一个区块候选数中时,就可以把该数字自包含该区块的行或列之其他区块候选数中删减掉落.应用“找出某一行.某一列或某一个九宫格各个区块候选数中只消失一次的数字来,并将该数字自包含该区块的另一个行.列或九宫格的其他区块候选数中删减掉落”的办法就叫做区块删减法 (Locked Candidates, Single Sector Candidates).区块删减法示例区块删减法一共有4 种状态:第一种是产生在行而去删减九宫格.第二种是产生在列而去删减九宫格. 第三种是产生在九宫格而去删减行.第四种是产生在九宫格而去删减列.<图 1> 就是产生在行而去删减九宫格的例子了,其他的情况举例如下:<图 2><图 2> 是产生在列而去删减九宫格的例子:因为第 3 列的数字 6 只出如今 (3, 1)~(3, 3) 这一个区块, 所以可以将上左九宫格的另两个区块 (1, 1)~(1, 3).(2, 1)~(2, 3) 候选数中的数字 6 安然的删减掉落; 于是(1, 1)的候选数 2.6 将被删减成 2,消失了独一候选数啦!<图 3><图 3> 是产生在九宫格而去删减列的例子:因为上右九宫格的数字 5 只出如今 (3, 7)~(3, 9) 这一个区块, 所以可以将第 3 列的另两个区块 (3, 1)~(3, 3).(3, 4)~(3, 6) 候选数中的数字 5 安然的删减掉落; 于是(3, 3)的候选数 5.9 将被删减成 9,消失了独一候选数啦!<图 4><图 4> 是产生在九宫格而去删减行的例子:因为中心九宫格的数字 1 只出如今 (4, 5)~(6, 5) 这一个区块, 所以可以将第 5 行的另两个区块 (1, 5)~(3, 5).(7, 5)~(9, 5) 候选数中的数字 1 安然的删减掉落; 于是(8, 5)的候选数 1.3.7.8 将被删减成 3.7.8;同理,中心九宫格的数字7.8 都只出如今(4, 5)~(6, 6) 这一个区块,所以可以将第5 行的另两个区块(1, 5)~(3, 5).(7, 5)~(9, 5) 候选数中的数字 7.8 都安然的删减掉落;于是(8, 5)的候选数 3.7.8 将再度被删减成 3;消失了独一候选数啦!像<图1>~<图3>如许,只做一次区块删减就找到下一个解的情况固然是不错,但有时并没有那么顺心, 像<图 4>就须要删减三次才得到下一个解,不过那还算好的了,因为三次的删减都正好产生在统一个区块中, 请看下面产生在不合区块的情况吧!。