霍普金森压杆实验报告

简述“霍普金斯”杆测量材料动态应力应变曲线的原理；选用一种大型软件对其进行计算模拟，并对模拟结果进行分析。

答：选用ABAQUS大型有限元软件一、“霍普金斯”压杆理论：Hopkinson压杆技术源于1914年B．Hopkinson测试压力脉冲的试验工作，后来R．M．Davies对它进行了改进。

1949年，H．Kolsky在这些基础上建立了进行材料单轴动态压缩性能试验的试验方法，测试了高应变率下金属材料的力学性能，这个方法称为分离式Hopkinson压杆(或Kolsky杆)技术。

其原理是将试样夹持于两个细长弹性杆(入射杆与透射杆)之间，由圆柱形子弹以一定的速度撞击入射弹性杆的另一端，产生压应力脉冲并沿着入射弹性杆向试样方向传播。

当应力波传到入射杆与试样的界面时，一部分反射回入射杆，另一部分对试样加载并传向透射杆，通过贴在入射杆与透射杆上的应变片可记录入射脉冲，反射脉冲及透射脉冲，由一维应力波理论可以确定试样上的应力、应变率、应变随时间的变化，以及应力、应变曲线。

5O多年来，此技术广泛用在高变形速率下材料力学性能的测试。

研究人员也对Hopkinson压杆试验方法进行了系统深入的研究，使该技术不断地改善和发展。

J．Harding 等在1960年将用于单轴压缩试验的Hopkinson压杆推广到了单轴拉伸试验，在此基础上，1983年又提出至今被广泛使用的Hopkinson拉杆试验方法。

W．E．Backer等、J．D．Campbell 等、J．Dully等又提出了Hopkinson扭杆技术，可对于试样施加高应变速率的纯扭转载荷。

为提高试验精度，前人在应力波的弥散效应、三维效应、应力波分离、试样中的瞬态平衡对试验结果的影响等方面做了大量工作。

分离式Hopkinson压杆实验的示意图如下：图8-1 分离式Hopkinson压杆示意图上图表示了压杆、试件和测试仪器等的位置安排。

压杆由高强度合金钢制成。

压杆与试件的接触面需要加工得很平并且保持平行。

A N S Y S L S-D Y N A数值模拟霍普金森压杆试验ANSYS/LS-DYNA数值模拟霍普金森压杆试验1 功能概述大多数材料在强度等力学性质方面都表现出某种程度的加载率或应变率敏感性，高幅值短持续时间脉冲和荷载所引起材料力学性质的应变率效应，对于抗动载的结构设计和分析是非常重要的。

这些动载来至常规武器侵彻与爆炸、偶然爆炸和高速撞击等许多军事和民用事件，对于这些事件的理论分析和数值模拟必须知道材料的高应变率强度、断裂特性和应力-应变关系等本构性质。

要研究材料在脉冲动载作用下的力学性质的实验设备和实验必须模拟类似现场的应变率条件，分离式霍普金森杆被公认为是最常用最有效的研究脉冲动载作用下材料力学性质的实验设备。

数值模拟是一种依靠电子计算机对工程问题和物理问题乃至自然界各类问题进行研究的技术。

它利用材料的本构函数，结合有限元或有限容积的概念，采用数值计算和图像显示的方法，因此具有如下优势：（1）检验理论结果是否正确；（2）弥补实验与观测得不足；（3）利用模拟结果，了解非线性过程中的因果关系与主要物理机制；（4）预测在不同初始条件与边界条件下非线性过程的发展情形；（5）数值模拟成本低，可以带来巨大社会经济效益。

由于很多材料的本构性质已经知道，因此在设计产品时，可以利用材料的本构性质通过仿真来模拟复杂的系统。

ANSYS/LS-DYNA数值模拟霍普金森压杆试验，就是通过ANSYS/LS-DYNA软件来模拟霍普金森压杆实验，通过设置弹丸不同速度，对试件进行研究。

霍普金森压杆实验分为自由式和分离式两种，本仿真采用分离式的办法。

2 原理简介2.1 霍普金森压杆实验简介霍普金森杆实验装置的基本原型最早是由Hopkinson提出的，它可用于测量冲击载荷的脉冲波形。

1949年Kolsky将压杆分成两段，试件置于输入杆和输出杆中间，通过加速的质量块、短杆撞击或炸药爆轰产生加速脉冲，利用这一装置可测量材料在冲击载荷作用下的应力-应变关系。

机械工程学院研究生研究型课程考试答卷课程名称：材料动态特性实验（SHPB实验）考试形式：□专题研究报告□论文√大作业□综合考试评阅人：时间：年月日材料动态特性实验实验目的：1、了解霍普金森杆的实验原理和实验步骤；2、会用霍普金森杆测试材料动态力学性能。

1.SHPB 组成：Kolsky 在Hopkinson 压杆技术的基础上提出采用分离式 Hop-kinson 压杆 SHPB )技术来测定材料在一定应变率范围的动态应力 ── 应变行为 ,该实验的理论基础是一维应力波理论, 它通过测定压杆上的应变来推导试样材料的应力 ── 应变关系, 是研究材料动态力学性能最基本的实验方法之一。

为了测出A3钢（又称Q235钢）的屈服极限、弹性模量以及其他性能参数。

用SHPB 实验就行数据测量。

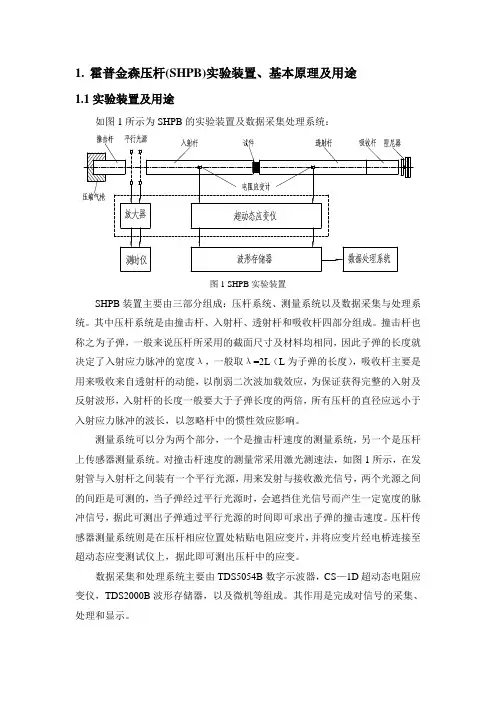
SHPB 的实现装置如下图：分离式Hopkinson 压杆装置示意图它由压缩气枪、撞击杆、测时仪、输入杆（入射杆）、超动态应变仪、试件、透射杆、吸收杆、阻尼器和数据处理系统组成。

2.实验原理：SHPB 技术建立在两个基本假定的前提上：（1）杆中应力波是一维波；（2）试件应力/应变沿其长度均匀分布。

根据垂直入射应力波在界面出的反射、透射原理和上述假定由：应力相等：)()()(t t t T R I σσσ=+ (1)应变相等：)()()(t t t T R I εεε=+ (2)式中()I t σ和()R t σ分别为入射杆的入射应力和反射应力，()T t σ为透射杆的透射应力，()I t ε和()R t ε为入射杆的入射应变和反射应变，()Tt ε为透射杆的透射应变。

图1 输入杆-试件-输出杆相对位置如图2所示，在满足一维应力波假定的条件下，一旦测得试件与输入杆的界面X 1处的应力，可理论推导得： []112()(,)(,)(,)2S I R T SA t X t X t X t A σσσσ=++ （3） SR I T S S L t X v t X v t X v L t X v t X v t ),(),(),(),(),()(11212--=-=ε （4） []⎰⎰--==t R I T S t S S dt t X v t X v t X v L dt t 01120),(),(),(1)(εε （5）式中：A 为压杆的横截面积，s A 为试件的横截面积，S L 为试件的长度。

霍普金森杆冲击力学试验霍普金森杆冲击力学试验，说到这个名字，听起来是不是有点儿高大上？其实啊，这玩意儿看起来复杂，做起来却能让你大开眼界，瞬间明白很多物理现象是怎么回事儿。

你要是觉得这种名字过于学术，那你就当它是“冲击测试”也行，简单来说，就是模拟物体在快速碰撞时的力学行为。

想象一下，你在滑板上玩得开心，然后突然撞上了个障碍物，啪的一声，你的身体瞬间停住，滑板却飞了好远。

这一瞬间发生了什么？冲击力有多大？如果再碰到不同的材料，力的变化会怎样？霍普金森杆就是用来解决这些问题的。

这个试验其实挺有意思的，它可以帮助我们了解材料在突然遭遇外力时的反应，不管是金属、塑料还是橡胶，甚至是你手机屏幕上的玻璃，都能用这个方法测试。

当我们说“冲击”时，脑袋里可能会想起什么赛车撞车啊，或者乒乓球拍打球那一瞬间的反应，但你要知道，这种瞬间的碰撞背后可隐藏着复杂的物理学原理。

霍普金森杆试验的核心就是通过撞击测试来研究材料如何吸收和传递这些突然的外力。

它的原理，简单点说，就是通过两根杆子、一个待测试的样品以及一些传感器来完成的。

试验的操作原理就像你在玩一个简单的“打击游戏”。

我们有一个很重的锤子，或者说是一个冲击源，它会猛烈地撞击到材料的表面。

而这时，冲击力会通过材料传递给接下来的几根钢杆。

等到这一力量传到材料的另一端，就能通过传感器测量这些变化，搞清楚材料在受到撞击时是如何变形的，力传递的速度是怎样的，以及它到底能承受多大的冲击力而不崩溃。

嘿，听起来有点像科幻电影里的实验室场景，是不是？而且啊，霍普金森杆试验的一个好处就是可以在极短的时间内完成。

你想想，物体一旦遭受冲击，瞬间发生的变化是非常剧烈的，如果要测量这些变化，光凭肉眼是不行的。

而通过霍普金森杆，我们就能精准地捕捉到冲击的全过程，所有的细节都不放过！通过这么快速、精准的实验数据，我们就可以知道，某个物体究竟在冲击力下能撑多久，是“顶住了”还是“断了”。

在许多高科技领域，尤其是航空航天、军事装备、汽车碰撞测试等，这种试验可说是“救命稻草”。

第1篇一、实验目的本实验旨在研究混凝土在不同动态载荷作用下的力学性能，包括抗压强度、抗拉强度、抗剪强度等，以期为混凝土结构设计提供理论依据。

二、实验原理混凝土动态性能实验主要基于霍普金森压杆（SHPB）试验方法。

SHPB试验方法是一种非破坏性试验方法，通过高速加载使试件在极短时间内承受高应变率下的动态载荷，从而研究混凝土在不同动态载荷作用下的力学性能。

三、实验材料1. 混凝土试件：采用C30级混凝土，试件尺寸为100mm×100mm×100mm，分别进行抗压、抗拉、抗剪试验。

2. 加载设备：霍普金森压杆试验机，加载速度范围为10～100m/s。

3. 测量设备：高速数据采集系统、应变片、力传感器等。

四、实验步骤1. 准备试件：将混凝土试件切割成100mm×100mm×100mm的立方体，试件表面磨光，确保试件尺寸和形状符合要求。

2. 安装试件：将试件放置于试验机的加载平台上，确保试件中心与加载平台中心对齐。

3. 连接传感器：将应变片和力传感器安装在试件上，确保传感器与试件连接牢固。

4. 设置试验参数：根据试验要求设置加载速度、应变率等参数。

5. 进行试验：启动试验机，使试件在高速加载下承受动态载荷，记录试验数据。

6. 数据处理与分析：对试验数据进行处理和分析，得出混凝土在不同动态载荷作用下的力学性能。

五、实验结果与分析1. 抗压强度实验结果表明，C30级混凝土在不同动态载荷作用下的抗压强度随应变率的增加而降低。

在应变率为10m/s时，抗压强度为50.2MPa；在应变率为100m/s时，抗压强度为45.6MPa。

这说明混凝土在高速加载下抗压强度有所降低，且应变率对其抗压强度有显著影响。

2. 抗拉强度实验结果表明，C30级混凝土在不同动态载荷作用下的抗拉强度随应变率的增加而降低。

在应变率为10m/s时，抗拉强度为2.8MPa；在应变率为100m/s时，抗拉强度为2.5MPa。

9.3 Hopkinson实验技术Kolsky于1949年提出了分离式Hopkinson压杆实验系统。

该装置采用应变片测量得到弹性压杆中的加载脉冲和输出杆中的透射脉冲，间接的推算得到夹在这两根杆中材料试件的动态本构关系，避开了冲击作用下直接测量试件中应力和应变的困难。

并经过几十年的发展形成了比较完整的Hopkinson实验技术，在材料的动态性能试验中得到了广泛的应用。

测试材料在高应变率的应力应变行为通常采用的是分离式Hopkinson压杆装置（Split Hopkinson Pressure Bar），简称SHPB实验装置。

SHPB实验技术已广泛应用于工程材料在高应变率下（102s-1～104s-1）的动态应力—应变曲线的研究。

它结构简单，操作方便，测量方法巧妙，加载波形易于控制。

当材料在受冲击时瞬间变形可近似地视为恒应变率，而应变率效应是工程上关心的问题之一。

目前在国内外该类装置已得到了广泛的应用。

9.3.1 SHPB实验技术SHPB实验技术是基于弹性脉冲在圆杆中传播的初等理论而发展起来的实验技术。

是目前测量材料在高应变率（102s-1～104s-1）下动态应力—应变曲线最普遍的方法。

Hopkinson .B .是最早在实验室条件下研究应力脉冲的学者之一。

他于1914年利用压力脉冲在杆自由端反射时变为拉伸脉冲的特性设计了一套装置，用来测定炸药爆炸或子弹打击时压力与时间的关系。

这套装置称为Hopkinson压杆，简称HPB（Hopkinson Pressure Bar）。

Hopkinson压杆的主体是一个圆柱形钢杆，长约1000mm，直径25mm，由四条线挂成水平状，这些线可在垂直面内摆动。

其装置示意图如图9-1所示，在杆的一端接一个称为测时器的短柱体，杆的另一端称为打击端，承受炸药爆炸或子弹打击造成的瞬时压力脉冲。

测时器和杆的直径相同，并用同种材料制成。

测时器和杆的接触面处磨得很平，涂以少许机油，可使压力脉冲通过接触面时不受影响，但几乎不能承受压力。

霍普金森压杆(SHPB)试验报告一、SHPB试验目的及用途1、了解霍普金森压杆(SHPB)测试的试验原理，掌握试验的基本操作步骤；2、霍普金森压杆(SHPB)测试技术主要用来测试材料在高应变率下的力学性能。

此试验主要通过霍普金森压杆(SHPB)测试技术，来测试泡沫铝(37mm×21mm)的力学性能，获取应力-应变曲线。

二、SHPB试验装置及其示意图1—发射气枪2—撞击杆3—激光发射器4—激光接收器5—电阻应变片6—入射杆7—试件8—透射杆9—吸收杆10—缓冲装置11—超动态应变仪12—波形存贮器13—数据处理系统三、试验原理1、三种波形的获取过程通过发射气枪作用，赋予撞击杆一定的初速度，此初速度可以由激光发射器和接收器测出间隔时间，然后计算得出。

撞击杆以此速度撞击入射杆，输入入射波脉冲，随着入射波的传播，在试件表面产生反射和穿透。

入射、反射、透射脉冲均可以通过电阻应变片测出，进而通过超动态应变仪传递到波形存贮器进行保存三种波形，从而利用入射、反射和透射脉冲来推导出试件中的应力、应变和应变率。

2、应力应变曲线获取的原理利用这些脉冲信号来获得材料在高应变率下的应力-应变曲线原理如下：图SHPB系统加载示意图上图是SHPB系统加载过程的示意图，Iε、Rε、Tε分别表示的是应变片测量到的入射、反射和透射信号。

1、2分别是试件的两个端面，S A是试件的横截面积，L是试件的长度，A和E分别是压杆的横截面积和弹性模量。

根据一维应力波理论，试件的两个端面的位移1u和2u可分别表示为1010t u C dt ε=⎰ (1) 2020tu C dt ε=⎰ (2)式中，1ε、2ε分别是试件两个端面的应变，0C 是压杆的弹性波速。

由于入射波到达杆与试样接触端是立刻会有反射波产生，因此入射杆与试件接触面上的应变1ε既包括了向右传播的应变脉冲I ε，又包括向左传播的反射应变脉冲R ε，即：1I R εεε=+ (3)因此界面1上的位移1u 就可以表示为：100()t I R u C dt εε=-⎰ (4)而界面2处的位移2u 只与透射脉冲T ε有关，故有：200t T u C dt ε=⎰ （5）这里的应变均是压应变。

霍普金森杆拉伸实验原理协议双方1.1 转让方（债权人）姓名：____________________________1.2 受让方（新债权人）姓名：____________________________1.3 债务人姓名：____________________________债务详情2.1 债务金额：人民币（￥）____________________________2.2 债务产生日期：____________________________2.3 原债务协议编号（如有）：____________________________转让细节3.1 转让日期：____________________________3.2 转让金额：人民币（￥）____________________________3.3 转让协议编号（如有）：____________________________转让条件和方式4.1 转让的具体条款：____________________________4.2 债务人同意的方式：____________________________4.3 转让费用（如有）：人民币（￥）____________________________4.4 支付方式：____________________________双方权利义务5.1 转让方的义务：____________________________5.2 受让方的义务：____________________________5.3 债务人的义务：____________________________违约责任6.1 违约责任条款：____________________________6.2 赔偿金额和方式：人民币（￥）____________________________其他条款7.1 适用法律：____________________________7.2 争议解决方式：____________________________7.3 协议生效日期：____________________________7.4 协议终止条款：____________________________签署转让方（债权人）：签名：____________________________日期：____________________________受让方（新债权人）：签名：____________________________日期：____________________________债务人：签名：____________________________日期：____________________________本协议一式 ___________ 份，转让方、受让方和债务人各执一份，自各方签署之日起生效。

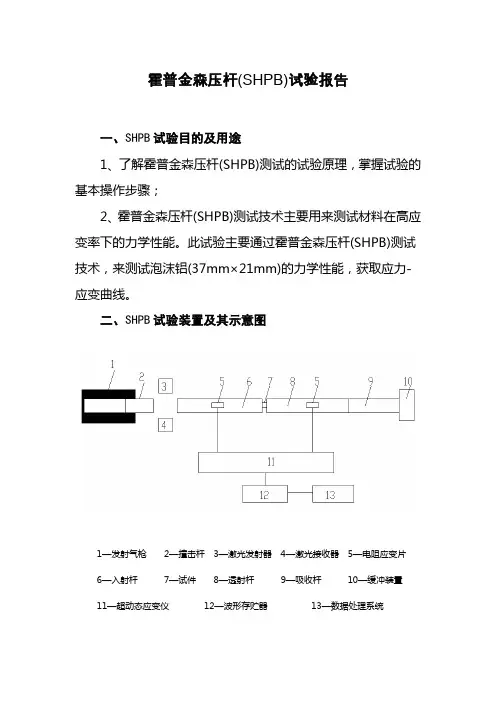
直接撞击式大变形霍普金森压杆实验技术陈浩;郭鑫;宋力【摘要】As a major method of mechanical property test under high strain rate, the time duration of the Hopkinson Bar test is limited by the length of the pressure bars, and the specimen can't achieve large deformation in a wide range of strain rate. In this paper, an experimental technique for large deformation loading with finite bar length is presented. The traditional method of direct impact test for ultra-high strain rate test has been applied to the dynamic performance testing of materials in relatively lower strain rate. Using this technique, the dynamic stress-strain curve of materials under the strain rate in the order of 102s-1can be obtained. Practical application shows that the method is simple and effective. The range of application of the technique, the geometrical parameters of the experimental device and the influence of the material parameters on the test results are also discussed.%作为高应变率材料力学性能测试的主要手段, 霍普金森压杆实验的测试时长受到压杆长度限制, 试件无法在较宽广的应变率下实现大变形. 由此提出了一种在有限杆长下实现大变形加载的实验技术, 该技术将传统上用于超高应变率实验的直接撞击方法应用于较低应变率下的材料动态性能测试, 可实现102s-1量级应变率下材料较大变形下的动态应力—应变曲线测试. 实际应用表明该方法简单有效. 并且文中也对该技术的适用范围、实验装置的几何参数及材料参数对测试结果的影响进行了分析讨论.【期刊名称】《宁波大学学报（理工版）》【年(卷),期】2018(031)004【总页数】4页(P70-73)【关键词】直接撞击;霍普金森压杆;大变形【作者】陈浩;郭鑫;宋力【作者单位】宁波大学机械工程与力学学院, 浙江宁波 315211;宁波大学机械工程与力学学院, 浙江宁波 315211;宁波大学机械工程与力学学院, 浙江宁波315211【正文语种】中文【中图分类】O347.4在动态加载条件下, 工程材料的力学特性通常采用应变率相关的本构方程来描述, 材料动态力学特性的差异则通过其本构参数来体现. 由于材料的相关本构参数无法用理论分析方式得到, 而必须通过材料动态加载实验来确定. 分离式霍普金森压杆(SHPB)或Kolsky杆是现今使用最为广泛, 并被认为可有效地应用于测试材料高应变率下力学特性的实验装置[1], 常用来测试各种工程材料在102~104 s-1应变率范围内的动态应力—应变曲线[2-3]. 与其他测试技术相比, 霍普金森压杆实验具有加载平稳可控、测试精度高、装置耐用可靠等优势. 然而经典的霍普金森压杆也存在某些不足, 其测试时长受到压杆系统的总长限制, 而且经典数据处理方法要求在测试上满足杆中左行、右行波的明确分离, 因此对于长度为L的撞击杆, 通常要求入射杆长度Li大于2L, 透射杆长度Lt等于或略小于入射杆, 而加载持续时间小于2L/C0(C0为杆中一维应力波速). 这样, 在装置总长度有限的情况下, 霍普金森压杆实际上只能在较高应变率下实现较大的实验应变, 而在102 s-1量级的应变率下不能或很难实现满足需要的试件变形.为使试件在测试中达到足够大的应变, 最直接方法是采用超长SHPB实验系统, 其优点是可以采用通常的霍普金森压杆实验方式、脉冲整形技术及数据处理方法. 不过超长实验系统的空间要求、系统加工难度及成本都远高于常见的SHPB装置, 因此其虽有应用, 但仍较为少见. “慢杆”技术则是另一种可实现大变形实验的方案, 由Zhao等[4]提出, 它由液压加载系统、压杆系统及相应的应力波反演数据处理软件组成, 但其结构较复杂, 也较少使用. 出于应用的需要, 我们提出一种基于传统霍普金森压杆系统的直接撞击式大变形实验技术, 可以在现有测试装置上很好地实现大变形冲击实验, 能够在102s-1量级应变率下测得材料的动态应力—应变曲线. 最早由Dharan等[5]提出直接撞击式霍普金森杆压杆技术, 后由Gorham等[6]予以改进, 该技术是出于对高应变率(104s-1量级)冲击压缩实验需要而提出的. 实际上, 该技术也可方便地用于102s-1量级应变率下的常规测试, 或103 s-1量级应变率下的大变形测试上.对于图1所示的实验方式, 在引入应力均匀性假设及适当简化的前提下, 试件的应变率、应变、应力可由下式计算:式中, MB及VB分别为撞击杆的质量及初速度; E0为压杆材料的弹性模量; C0为杆中一维应力波波速; 是仅由于试件作用所引起的透射杆中的右行应力波, 在测试时间较长时, 需要通过应力波反演来确定.在利用直撞式方案进行测试时, 可以采用应力波分离技术来实现长时实验[7]. 设透射杆长度为L0, 其上记应变片距接触试件一端的距离为a, 应变片测得信号为, 压杆横截面面积为A0.记,对于图1的测试系统可写为:其中:最后可得:采用上述直撞击杆分别对一种铜合金材料及一种有色金属多孔材料进行了测试, 试件统一尺寸为1cm×1cm×1cm, 实验中使用Φ37钢质压杆, 透射杆杆长2m, 撞击杆杆长0.8m.图2~图3即为2种材料的测试结果. 从图中可见, 对于测试的实体铜合金试件, 最大工程应变可以达到0.6左右, 而多孔金属材料实验最大工程应变可达0.9, 并且同时实验中应变率下降程度在可接受范围, 而上述结果在传统霍普金森压杆系统上(超长压杆系统除外)是难以实现的.此外, 从图2和图3还可以看到, 直撞式压杆的实验应变率总随着时间的增加呈下降趋势. 实际上对于特定装置, 其在实验过程中的应变率总是有所变化的, 这种变化与试件、压杆系统有关. 而有效的霍普金杆压杆实验需要实验中试件的应变率具有某种程度的恒定性, 为此引入应变率下降率, 其中, 为实验的初始工程应变率, 为实验中止时的应变率. 对于直接撞击霍普金森压杆系统, 可以采用限定的方式来提出应变率恒定性要求.从满足工程需要角度出发, 可从平均意义上来讨论实验中应变率的下降问题, 此时可将撞击杆与透射杆近似视为刚体. 记被测材料的平均屈服应力为Ys, 横截面面积为As, 试件高度为H, 撞击杆质量为, 透射杆质量为, 设试件左右端面的运动速度分别为和, 参考图1可写出:上式中实验初始工程应变率为, 实验中止时的应变率为.近似取测试过程中试件平均应变率为:此时需注意到实验中止时()试件最大应变, 利用式(8)对特定可给出条件:式(9)可作为实验设计的依据, 即在给定实验应变率下降及最大实验应变要求的情况下, 公式应得到满足. 图4则是基于式(9)的软件小工具对图2中实验相关设计参数进行验证的结果.实际应用中, 在提出实验要求后, 可以用式(9)来进行相关参数的选择及其评价. 例如, 对某种平均屈服应力为200MPa的材料, 采用Φ74mm, 长3m的撞击杆与透射杆, 在试件截面为8mm×8 mm×12mm, 实验应变率降幅为0.2, 且待测最大应变为0.1的条件下, 其实验平均应变率下限约在102s-1左右.本文提出了采用直接撞击来实现材料大变形冲击压缩动态应力—应变曲线测试的实验方法, 结果显示能有效地实现冲击大变形实验, 效果良好, 简单易行; 且给出了直撞式压杆实验的设计条件准则, 便于工程应用.直撞式实验时, 试件中应力均匀性是需要考虑的问题. 从理论分析来看, 直接撞击实验时, 试件中的应力均匀性相对较差, 但对于实体材料测试而言, 由于其在较低应变率下变形时间较长, 因此在大多数情况下可满足均匀性要求[8]. 而当直撞式压杆用于软体材料或泡沫材料测试时, 更容易实现大变形及较低的实验应变率, 但由于此类材料中的应力波波速通常很低, 此时均匀性问题就需要有针对性地予以考虑.文中所提方案中可以采用更长的撞击杆. 从实现大变形的角度, 当撞击杆与透射杆等径, 撞击杆与透射杆等长时为最佳设计. 但在使用长撞击杆时, 应力波在其中的传播应予以考虑, 采用与透射杆中类似的反演方法, 技术上并无困难.直撞式霍普金森杆的一个不足之处是其所测应力—应变曲线的初始段较标准霍普金森杆实验所测曲线初始段更为倾斜, 主要原因是由于其试件与压杆间的接触相对不够理想所致. 尽管一般认为霍普金森杆实验所测得的弹性段是无效的, 但仍可考虑引入某种修正来予以解决.【相关文献】[1] Gray III G T. Classic Split-Hopkinson Pressure Bar Testing[M]//Kuhn H, Medlin D. SAM Handbook, Mechanical Testing and Evaluation, Vol. 8, Materials Park, OH: ASM International, 2000:462-476.[2] Chen W W, Song B. Split Hopkinson (Kolsky) Bar: Design Testing and Applications[M]. New York: Springer Press, 2015.[3] 韩李斌, 杨黎明. 泡沫混凝土动态力学性能及破坏形式[J]. 宁波大学学报(理工版), 2017,30(1):68-72.[4] Zhao H, Gary G. A new method for the separation of waves: Application to the SHPB technique for an unlimited duration of measurement[J]. Journal of the Mechanics & Physics of Solids, 1997, 45(7):1185-1202.[5] Dharan C K H, Hauser F E. Determination of stress-strain characteristics at very high strain rates[J]. Experimental Mechanics, 1970, 10(9):370-376.[6] Gorham D A, Pope P H, Field J E. An improved method for compressive stress-strain measurements at very high strain rates[J]. Proceedings: Mathematical and Physical Sciences, 1992, 438(1902):153-170.[7] Park S W, Zhou M. Separation of elastic waves in split Hopkinson bars using one-point strain measurements[J]. Experimental Mechanics, 1999, 39(4):287-294.[8] 宋力, 胡时胜. SHPB测试中的均匀性问题及恒应变率[J]. 爆炸与冲击, 2005, 25(3):207-216.。

11—超动态应变仪 12—波形存贮器 13—数据处理系统霍普金森压杆 (SHPB) 试验报告一、 SHPB 试验目的及用途1、了解霍普金森压杆 (SHPB) 测试的试验原理， 掌握试验的 基本操作步骤；2、霍普金森压杆 (SHPB) 测试技术主要用来测试材料在高应 变率下的力学性能。

此试验主要通过霍普金森压杆 (SHPB) 测试 技术，来测试泡沫铝 (37mm ×21mm) 的力学性能， 获取应力 -应变 曲线。

二、 SHPB 试验装置及其示意图1 —发射气枪 2—撞击杆 3 —激光发射器 4—激光接收器 5 —电阻应变片 6—入射杆7—试件8—透射杆9—吸收杆10—缓冲装置三、试验原理1、三种波形的获取过程通过发射气枪作用，赋予撞击杆一定的初速度，此初速度可以由激光发射器和接收器测出间隔时间，然后计算得出。

撞击杆以此速度撞击入射杆，输入入射波脉冲，随着入射波的传播，在试件表面产生反射和穿透。

入射、反射、透射脉冲均可以通过电阻应变片测出，进而通过超动态应变仪传递到波形存贮器进行保存三种波形，从而利用入射、反射和透射脉冲来推导出试件中的应力、应变和应变率。

2、应力应变曲线获取的原理利用这些脉冲信号来获得材料在高应变率下的应力-应变曲线原理如下：1 2上图是SHPB 系统加载过程的示意图，I、R、T分别表示的是应变片测量到的入射、反射和透射信号。

1、2 分别是试件的两个端面，A S是试件的横截面积，L是试件的长度，A和E 分别是压杆的横截面积和弹性模量。

根据一维应力波理论，试件的两个端面的位移u1和u2可分别表示为(7)(8)tu 1 0C 0 1d t(1) tu 2 0C 0 2d t(2)式中， 1、 2分别是试件两个端面的应变， C 0是压杆的弹性 波速。

由于入射波到达杆与试样接触端是立刻会有反射波产生， 因此入射杆与试件接触面上的应变 1既包括了向右传播的应变脉冲 I，又包括向左传播的反射应变脉冲即：(3)因此界面 1 上的位移 u 1就可以表示为：而界面 2 处的位移 u 2只与透射脉冲 T有关，故有：5)这里的应变均是压应变。

1、霍普金森压杆实验中的一些问题的现状:关于霍普金森压杆技术有效性的讨论过去主要集中试件的尺寸效应，波在杆中的二维弥散修正等。

实验过程中试件是否处于应力均匀状态以及试件是否以恒应变率变形这两个问题上所给予的关注并不多，或者说还没有找到一个非常可行的方法来解决这两个问题。

2、常规霍普金森压杆技术所遇到的问题：要得到有效并精确的数据，下列霍普金森压杆的假设必须得到满足：1）压杆中的波传播必须是平面一维的，因为应变片所测得的杆的表面应变通常代表压杆整个横截面上的轴向应变。

2）试件中的应力和应变均处于均匀状态3）此外，为保证得到有效的应力—应变数据，还应该使试件中的应变随时间变化的历史也是均匀的，即试件的变形是在恒应变率的条件下进行的。

所对应的问题：1）二维波动效应(或称为波的弥散效应)2）在高应变率霍普金森压杆实验中，加载的上升时间在10μs左右，高速撞击将导致明显的应力波传播效应（纵向惯性效应），低应变率下的试件中应力均匀性的结论不再成立，因而这时的试件也不可能处于实际的应力均匀状态3）在常规霍普金森压杆实验中，子弹的撞击在入射杆中产生一个梯形的入射脉冲。

由于试件横截面的增加和试件材料的硬化，应变率则会随时间减小以致于不能在整个实验中保持为一恒定值3、常规霍普金森压杆对不同材料测试时存在的主要问题：3.1金属类材料：因为金属的弹性行为发生在非常小的变形下，在这样的小变形下，要得到精确的实验数据，因弥散效应引起的波的振荡问题和试件中应力均匀性是必须要考虑的敏感问题。

3.2脆性材料：首先，在霍普金森压杆实验中必须保持脆性材料试件两个端面严格平行以增加实验数据的精度，因为试件端面的不平行或不平整都可能导致局部失效和应变测量的不精确。

其次，常规霍普金森压杆实验中陡峭的梯形脉冲也导致脆性试件在小变形下的严重应力不均匀。

此外，经典的梯形入射脉冲还会导致脆性材料试件非恒应变率变形。

可以概括地说，对这样的脆性材料而言，常规霍普金森压杆已不能满足在脆性材料实验中恒应变率和应力均匀性的要求以致于难以获取有效的动态实验结果。

100mm/75mm/50mm/20mm霍普金森压杆Hopkinson压杆【2 】一. Hopkinson压杆构成霍普金森多功效压杆装备重要由储气装备.发射体系.杆系与枪弹.量测体系.中间支持部件.基本导轨.缓冲装配和帮助装备等构成.1 .发射体系：由储气室.发射体.汽缸.活塞.联接体.支承座.多种可改换炮管.反后座支架等构成.压力最高可达5.8MPa ,炮管内径可实现为Φ 7 5 , Φ 20 等多种规格,长度为3m .2 .杆系与枪弹：分两种材料：（1）弹簧钢,热处理,规格Φ 7 5 ,Φ 20 ,最大长度3m .（2）超硬铝LC4 规格Φ 7 5 ,Φ 20 , 最大长度3m .3 .中间支持部件：由基座.三向移动锁定定位机构.高精度轴承.压盖.手念头构等构成.重要特色在同一基准导轨下可使不同直径杆系沿轴向活动为滚动摩擦.滑动轻快,自调剂极其便利.4 .基本导轨：由多根铸铁地轨.地脚调节装配等拼合构成的一条整体导轨.应用专用技巧,使导轨在安装好后,形成两个基准：一个是侧基准,一个是程度基准,可使发射装配.杆系.支持部件等在同一基准下工作,大大进步调试工作效力.整体基准直线度可掌握在0.04/m 以内.二.体系指标： 1 .压力规模：0.2~5.8MPa2 .杆系直径：两种：Φ 7 5 ,Φ 20 .3 .枪弹速度：≤ 40m /s4 .杆件材料：弹簧钢.超硬铝LC4 ,均热处理.5 .导轨长度：12.4m6 .实用杆件直径规模：Φ20 ~ Φ 75三. 动态紧缩实验1测试体系传统的Hopkinson压杆测试体系包括有：加载体系.动态应变仪.数据记载与采集体系和数据剖析盘算体系,如图1所示.图1 分别式Hopkinson压杆实验道理图1.1.2测试道理Hopkinson压杆装配的焦点部分是两段分别的弹性波导杆,即输入杆和输出杆,试样夹在两杆之间.加载脉冲由撞击杆撞击输入杆的端部产生.撞击杆在压气枪中由高压气体的推进感化被加快到必定的撞击速度,以此速度撞击输入杆的端部,产生一个中断时光取决于撞击杆长度的入射弹性压力脉冲.当初始的压力脉冲经撞击杆的自由端反射成为一个拉力脉冲并回到撞击面时,撞击杆就完成了对输入杆的卸载,因而在输入杆中将产生波长为撞击杆长度两倍的入射应力波.当输入杆中的入射应力波到达试样时,一部分因为杆和试样横截面积不等和波阻抗不匹配而反射回输入杆形成反射应力波,另一部分则穿过试样到达输出杆形成透射应力波,透射应力波再由接收杆捕获,最后由能量捕收器接收.装配见图如图1所示.1.2 动态拉伸实验1.2.1测试体系图2 改良的Hopkinson杆测试体系传统的Hopkinson杆实验装备重要用于测试材料的动态紧缩力学机能参数,改良后的Hopkinson杆则可以实现动态拉伸实验,图2给出的是加载板状拉伸试样的加载装配示意图.测试体系包括：加载体系.动态应变仪.数据记载与采集体系和数据剖析盘算体系等.1.2.2测试道理测试记载的入射.反射.透射脉冲分别用..表示,依据试样与拉杆的界面前提,按一维弹性波传播理论可盘算得到试样中的应力.应变以及响应的应变率大小,其盘算公式与动态紧缩实验中的公式一样.备注：此体系为定制产品,重要规格有100mm,75mm, 50mm, 20mm等,迎接宽大客户来电咨询.。

ANSYS/LS—DYNA数值模拟霍普金森压杆试验1 功能概述大多数材料在强度等力学性质方面都表现出某种程度的加载率或应变率敏感性,高幅值短持续时间脉冲和荷载所引起材料力学性质的应变率效应，对于抗动载的结构设计和分析是非常重要的。

这些动载来至常规武器侵彻与爆炸、偶然爆炸和高速撞击等许多军事和民用事件,对于这些事件的理论分析和数值模拟必须知道材料的高应变率强度、断裂特性和应力—应变关系等本构性质.要研究材料在脉冲动载作用下的力学性质的实验设备和实验必须模拟类似现场的应变率条件，分离式霍普金森杆被公认为是最常用最有效的研究脉冲动载作用下材料力学性质的实验设备.数值模拟是一种依靠电子计算机对工程问题和物理问题乃至自然界各类问题进行研究的技术。

它利用材料的本构函数，结合有限元或有限容积的概念，采用数值计算和图像显示的方法,因此具有如下优势:（1）检验理论结果是否正确；（2）弥补实验与观测得不足;（3）利用模拟结果，了解非线性过程中的因果关系与主要物理机制；（4）预测在不同初始条件与边界条件下非线性过程的发展情形;（5）数值模拟成本低,可以带来巨大社会经济效益。

由于很多材料的本构性质已经知道，因此在设计产品时，可以利用材料的本构性质通过仿真来模拟复杂的系统。

ANSYS/LS—DYNA数值模拟霍普金森压杆试验，就是通过ANSYS/LS-DYNA软件来模拟霍普金森压杆实验，通过设置弹丸不同速度，对试件进行研究.霍普金森压杆实验分为自由式和分离式两种，本仿真采用分离式的办法.2 原理简介2。

1 霍普金森压杆实验简介霍普金森杆实验装置的基本原型最早是由Hopkinson提出的,它可用于测量冲击载荷的脉冲波形。

1949年Kolsky将压杆分成两段,试件置于输入杆和输出杆中间，通过加速的质量块、短杆撞击或炸药爆轰产生加速脉冲,利用这一装置可测量材料在冲击载荷作用下的应力—应变关系。

Kolsky的工作是一项革命性改进，现代的分离式霍普金森杆都是在其基础上发展而来，所以分离式霍普金森杆也称之为Kolsky杆。