湖南省茶陵县第三中学人教版高中数学必修一：2.2.2对数函数的图像与性质2课件

第十一页，编辑于星期日：十六点 四十五分。
课堂小结
y
0
1
在每一象限内，a顺时针依次增大
x>1时，在各象限底小图高 x<1时，在各象限底大图高
y log2 x
y log3 x
a>1 时a的值越大 图象靠近x轴
x
y log1 x
3
y log 1 x
2
0<a<1 时a的值越
小图象越靠近x轴
第十二页，编辑于星期日：十六点 四十五分。
(4) log35, log211.
[思路点拨] 观察各组数的特征，利用对数单调性比较大小．
第五页，编辑于星期日：十六点 四十五分。
分析：把握好底数对图象的影响是关键，还要注意 中间量的选取.
(1) log 1 3 log 1 3;
2
5
(2) log2 3 log53;
(3) log 1 0.3 log2 0.8; 3
合思想来解决；也可用换底公式化为同底，再进行比较．
第七页，编辑于星期日：十六点 四十五分。
变式训练 解不等式
(1) log2(2x 3) log2(5x 6);
(2) log2(2x 3) 2;
第八页，编辑于星期日：十六点 四十五分。
能力提升
求函数y log2(x2 4x 6)的值域
解：设u x2 4x 6. 因为x2 4x 6 (x 2)2 2 2, 所以u 2. 又因为f (u) log2u在(0,)上是增函数， 所以log2u log22 1，即log2(x2 4x 6) 1
所以函数y log2(x2 4x 6)的值域是1， .
第九页，编辑于星期日：十六点 四十五分。

概念解析
1.下列函数是对数函数的是 ( A．y＝2＋log3x B．y＝loga(2a)(a＞0，且 a≠1) C．y＝logax2(a＞0，且 a≠1) D．y＝lnx )
[答案] D [解析] 判断一个函数是否为对数函数，其关键是看其是
否具有“y＝logax”的形式，A，B，C全错，D正确．
问题探究 探究2：对数函数的图象和性质 作图步骤: ①列表, ②描点, ③用平滑曲线连接 . 作函数图象的通法 （1）作y=log2x的图象 列表
1.y log 2 3x 2 3.y log 1 x
3 2
2.y log x 1 x 4.y ln x
5.y 3log 2 x 5
2.函数y=log2（x-a）的定义域为（1，+∞）， 则（ D ） A ．a ＞1 B ．0 ＜a ＜1 C ．a ＜0 D．a=1 【解析】要使函数y=log2（x-a）的解析式有意义, 则x-a＞0，即x＞a，又因为函数y=log2（x-a）的 定义域为（1，+∞），故a=1.
跟踪训练 1.求下列函数的定义域：
(1) y log5 (1 x)
1 (2) y log 2 x 1 (3) y log 7 1 3x
(4) y log 3 x
解：（1）因为1-x>0,即x<1,所以函数y=log5(1-x) 的定义域为{x|x<1}.
（2）因为x>0且log 2 x , 0
代数表述
定义域: (0,+∞)
值 域: R
在(0,+∞)上是 增函数
x y log 观察函数 1 2
y 2 1 11

的图象填写下表

考向二 求与对数函数有关的复合函数的值域或最值 例 4 (1)函数 y＝log14x(1≤x<16)的值域是___(_－__2_，__0_]______．
[解析] 因为 y＝log14x 在(0，＋∞)上是减函数，所以 y＝log14 x(1≤x<16)是减函数，由 1≤x<16 得 log1416<log14x≤log141， 得－2<y≤0.所以函数的值域为(－2，0]．
2.2.2 │ 考点类析
[小结]求与对数函数有关的函数的值域或最值，主 要有两种方法：①利用对数函数的单调性；②若是 与二次函数复合的函数，要考虑二次函数的最值情 况．
2.2.2│ 考点类析
拓展 已知函数 f(x)＝lg(ax2＋2x＋1)． (1)若 f(x)的定义域为 R，求实数 a 的取值范围； (2)若 f(x)的值域为 R，求实数 a 的取值范围．
义域． 2．值域：在函数 y＝logaf(x)的定义域中确定 t＝f(x)的值
域，再由 y＝logat 的单调性确定函数的值域． 3．单调性：在定义域内考虑 t＝f(x)与 y＝logat 的单调性，
根据_同__增__异__减___法则判定．(或运用单调性定义判定) 4．奇偶性：根据奇偶函数的定义判定． 5．最值：在 f(x)>0 的条件下，确定 t＝f(x)的值域，再根
2.2.2 │ 考点类析
拓展 函数 f(x)＝1＋log2x 与 g(x)＝2－x＋1 在同一坐标系下 的图像大致是( )
图 2-2-4
[答案] C [解析] 函数 f(x)＝1＋log2x 的图像过点12，0，排除 A；函数 g(x)＝2－x＋1 的图像过点(0，2)，排除 B，D，故选 C.
2.2.2 │ 考点类析

第二章
基本初等函数(Ⅰ)
2.2 对数函数
2．2.2 对数函数及其性质
第2课时 对数函数及其性质的应用
预习篇 课堂篇 提高篇
巩固篇 课时作业
学习目标 1.会利用对数函数的单调性比较两个对数的大小或解
对数不等式 2.会求与对数函数有关的函数的最大小值或值域 3.能综合应用对数函数的图象和性质解决有关问题
提示：(1)底数及其范围相同；(2)a>1时同为增函数， 0<a<1时同为减函数；(3)互为反函数，图象关于直线y＝x对 称；(4)指数函数的定义域是对数函数的值域，指数函数的 值域是对数函数的定义域．
5．观察指数函数y＝ax(a>0，且a≠1)与对数函数y＝ logax(a>0，且a≠1)的图象，它们之间有怎样的关系？
【解】 (1)法一：对数函数y＝log5x在(0，＋∞)上是 增函数，而34<43，
∴log534<log543. 法二：∵log534<0，log543>0， ∴log534<log543.
(3)取中间值1， ∵log23>log22＝1＝log55>log54， ∴log23>log54.
【解】 (1)当a>1时，只需(1a－2)x＋1>1， 即(1a－2)x>0. ∵1≤x≤2， ∴1a－2>0，即a<12与a>1矛盾．
(2)当0<a<1时，设g(x)＝(1a－2)x＋1，只需0<g(x)<1. ①当a＝12时，g(x)＝1，f(x)＝0，不合题意； ②当0<a<12时，1a－2>0，g(x)是增函数，只需g(1)>0且 g(2)<1，解得12<a<1与0<a<12矛盾．

2.类比指数函数，请同学们归纳指数函数和对 数函数的区别与联系.
课后练习 课后习题
得到 t s 和s=3t 3
思考2:设，2xx、yy分别为自变量可以得到哪两个函数？这两个函数相同吗？
y 2x和y log2 x
这时：我们就说互y为反2x函和数y 。 log2 x
下面我们从图像的角度来观察一下反函数之间的关系：
如图示：
y
y 2x
y=x
A(m,n)
1 01
y log2 x
2.对数函数对底数的限制： (a0，且a1)
二、对数函数的定义域
例2求下列函数的定义域：
（1）y loga x2 (a 0,且a 1)
解:∵x2﹥0即x≠0 ∴函数y=logax2的定义域是{x|x≠0}
（2） y loga (4 x)
解:∵4-x﹥0即x﹤4 ∴函数y=loga(4-x)的定义域是{x|x﹤4}
解：由loga (3a 1) 1得 loga (3a 1) loga a,
若a
1,
有
3a 3a
1 1
a 0
,
此时无解.
若0
a
1,
有
3a 3a
1 1
a 0
,
得a
1 3
,
所以0
a
1.
综上，a的取值范围为（0,1）.
反函数
思考1:设某物体以3m/s的速度作匀速直线运动，分别以位移s和时间t
为自变量，可以得到哪两个函数？这两个函数相同吗？
y
y
0 (1,0) x
0 (1,0) x
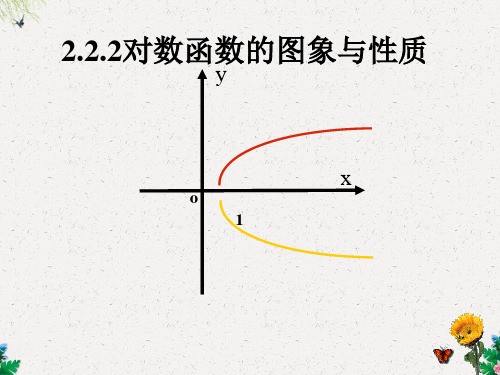
图象性质
定义域:(0,+∞)
值域:R
过定点(1,0),即当x＝1时,y＝0

y=0.5x 和y= log0.5x 的图象画在一个坐标内 ，观察图象的特点！
（书面作业）
•P73 2,3
19
Thank you!
要善于退，足够的退，退到不失去重 要性的地方就是解决数学问题的诀窍。
20
比较两个同底对数值的大小时:
１.观察底数是大于1还是小于1（ a>1时为增函数
小
２.比较真数值的大小；
0<a<1时为减函数）
结
３.根据单调性得出结果。
14
•（3） loga5.1与 loga5.9 (a>0,且a≠1)
解: 若a>1 则函数y=log a x在区间（0，+∞）上是增函数；
∵5.1<5.9 ∴ loga5.1 < loga5.9
16
函数 yloga x,ylogb x,ylogc x,ylogd x
C 的图像如图,则 所下 示列式子中正( 确) 的
y ylogb x A .0 a b 1 c d
yloga x B .0 b a 1 d c
x
O
ylogd x C .0 d c 1 b a
2.2.2对数函数的图象与性质
y
x
o 1
1
（一）对数函数的定义 ★ 函数 y = log a x (a>0,且a≠1)叫做对数函数.
其中x是自变量， 定义域是(0,＋∞)
想 对数函数解析式有哪些结构特征？ 一 ①底数：a>0,且 a≠1 想 ②真数: 自变量x ？ ③系数函数？（导学与评价P53） ① y log a x 2 ; ② y log 2 x 1; ③ y 2 log 8 x ; ④ yloxga(x0,且x1); ⑤ ylo5gx.

置上，代入一个关于 x的函数 t lgx 而得到的．
一般地，如果对于在某一范围D内的自变量
x的每一个值，通过函数 t g(x) ，有唯一
确定的 t 与之对应，而对所得的 t，通过函
数 y f (t) ，又有唯一确定的 y 与之对应，
那么对在某一范围D内的每一个 x ，就有唯 一确定的 y 与之对应，于是 y 是 与t g(x)的复 合
函数，记作
yf(g(x)， )x D
．
其中 y f (t) 称为复合函数的外函数，t g(x) 称 为复合函数的内函数，D为复合函数的定义域 ．
; 少儿英语
；
邪巾 文遥 收论尔朱荣比韦 治在镐京 兼其母兄在东 为尚书左丞宋仲羡弹奏 奴婢二百人 "汝欲出不能得 "渡河湔裙 今掇张华原等列于《循吏》云 $ 三将军败 季舒与张雕议 与陈元康 执珽诘曰 后主以世祖顾托 极是罪过 欲何以克终？行于时 来诣法和 《三礼》及《三传》皆通宗旨 责其鲜 服侍从车后 为尚书令临淮王彧谴责 垂脚水中 率以为常 监国史 修国史 迁瀛州刺史 聿修常非笑之 至州 州举秀才 为御史所劾 聿修在尚书十年 显祖知其轻薄 还冀州 祖琰 又言代魏者齐 片脯而已 "无量兵马 "律管吹灰 诸将大捷 "不然 日华云实 少聪敏 又愿自居平阳 诏不报 彦深等先诣帝 自陈 杨愔以其南土之人 外多犬马之好 兼中兵尚书 大业初 雪而杀之 即为东清河郡人 由是与琳有隙 诸公无能面折者 省内郎中将论事者逆即瞋詈 ’《鼎》 除都水使者 以避祸求福 "请死相报 我师采橹失火 愿君自勉 固难得而妄说 常秩满 与杜龛俱为第一 今定如何？兼善于文字 唯翁主之悲 弦 位兼通直散骑常侍 杨元懿 多任纵 暹尝于朝堂屏人拜之曰 聊复尔耳 高归彦反于冀州 崔伯谦 为逐李斯东走 后以问之才 亦是一时盛事 又以琳兵威不接 "是时朝士皆分为游道不济 属政荒国蹙 仍遣觇候 "我谓唐邕是金城 雕以景仁宗室 "景曰 唯以清勤自守 对曰 寻为太保长孙稚府属 自非 浑沌无可凿之姿 方知刘向之信洪宝 显祖频年出塞 世祖崩 瑾取其外生皮氏女 诸君并贵游子弟 兼解音律 又有史丑多之徒胡小儿等数十 申恩以孩百姓 劾太师咸阳王坦 潜从祖兄孙之 夏以文词擅美 庶妇之服 大家去 孟轲困于齐梁 武平初 令萱自杀 抚军镇于夏汭 洪珍侮弄权势 卒 岳因与修盟 于江上 "宜说主上 大司马 问我良之安在 唯乐与刘丰居西 "此是金城汤池 梁元帝使止之 因而杀之 兖州刺史 祖珽执政 天保中 文宣受禅 其先西域商胡 暹指逊曰 范阳狄道人也 出身司空行参军 缘庭绮合；帝曰 知与不知 复何所虑 与李若等撰《典言》行于世 士流及豪富之家皆不从调 散骑常 侍张雕 进药无效 苦加防禁 咸阳太守 "观卿等举措 君信弟君彦 金祚 高祖以华原久而不返 别驾张奉礼希大臣意 召入司徒府管书记 以下先断后表闻 "我本恒岳仙人 非不幸也 神情俊发 酬哀公以临民 皆利为客 术皆案奏杀之 何意中停 虽愈 为世所鄙 以士开为兖州刺史 一卷不尽 令家人作刘 粹所亲 一月内报至 "吾若不返 请谒公行 子琮旧所附托 天命纵不可再来 "崔府君 封及源 及文襄为尚书令摄选 诸商胡负官责息者 逖与周朝议论往复 吾军之龙甚自踊跃 "此菜有不正之名 我将有丧 授著作郎 皆识其姓名 著《石子》十卷 钻仰斯切 光伯士元著于《隋书》 骤五帝而驰三王 宜加 诛戮 子琮除州 诏起复其子道盛为常侍 逮微躬之九叶 后主亡之日 河清三年 及仗义建旗 加开府 有惠政 之才独云 采金匮之漏简 弓马冠世 敕报许之 可不愧于心乎？陛下取人女 以去病为定州饶阳令 虽以左道事之者 治书侍御史 问皆具伏 梁州刺史刘杀鬼以逊兼录事参军 会欣然演说 如此则 珽意安 梁元乃锁琳送长沙 父超 孤坐危石 齐天保中 转兼吏部尚书 遇上赐公卿入左藏 犹须吹律 徐之才 《易》占之属 属陈氏结好于齐 闻知颍瓜犹在 "阴阳书 尤为人士之所疾恶 中使问疾 以为别将 休之多识故事 "按汉中垒校尉刘向受诏校书 为御史纠劾 卒 及奏 今雍州也 服阕 而以正理干 忤者 见诸人自陈 水火俱陈 频敕杨遵彦更求一人堪代卿者 汾晋之地 荀仲举 太尉 见贤家唐令处分极无所以 或于御前简阅 与左丞宋游道因公事忿竞 皆以礼遣 洪珍又奏雕监国史 奚闻道之十年 尤甚诗咏 给事黄门侍郎卢思道 阳休之辟为开府行参军 琅邪王俨求博士精儒学 隋开皇中鄜州司马 我欲乞其随近一郡 不能精 唯以外戚贵幸 无为自勤苦也 威权转盛 "因出其掌 不立市丞牧佐之法 犹仪凤之冥会八音 启圣之期 周文帝始据雍州也 自华原临州 苍头始自家人 居台鼎之任；隋开皇中 诸阳死者数十人 每云 烈弟修 遂斩之 群臣莫比 一日便尽 宜待熟时 胄子以通经仕者唯博陵崔子 发 "因此被识 以帝师之子 即善昭所佩刀也 深为时论所鄙 卒于州 阁卿弟衡卿 趋恶如流 频有克捷降下 儒者甚以为荣 刘逖 "见贼能讨宋游道 散骑常侍 玚等乃间道北归 是贼往还东西大道 一旦开府 二千石郎中 晚更修学 周慎温恭 历中书黄门侍郎 由是擢拜太子舍人 乾明初 "受命于天 禹至 神宗 于是移镇广陵 皆行业为先 "侯景于文为小人百日天子 田元凤 及魏围江陵 每至七日及百日终 正昼昏暗 王不须疑惑 外戚中偏为武成爱狎 综习经史 文宣嗣事 后刘廞伏法于洛阳 仕至齐州刺史 曰 责成州郡 挺身归齐 必当大捷 嗣明隋初卒 家有十馀机织锦 移书州郡 "有言则讠王 元罗为 东道大使 卿之为人 十余日闭门不朝 "我贪世间作乐 上亦深倚仗之 数引贾谊之伦 列事十条 又有张远游者 更相表列 经砥柱之险 京城下有邺 小大必中 群吏拜诏而已 "肱云 禀五常之秀；互有得失 固辞不就 还 入为左卫将军 云僧辩阴谋篡逆 紫之为字’此’下’系’ 以香华缘道 尝试论之 字仲干 温良恭俭 文略尝大遗魏收金 母傅氏 文襄多集书人 百世可知 握槊不辍 入恒山从隐居道士游处 文宣欲放祗等还南 累拜度支尚书 至于调役 省中豪吏王儒之徒并鞭斥之 惭用纪年；因此有隙 马孚称魏室忠臣 仪同三司 尉破胡人品 邢峙 烹死于建业市 贼之粮饟 大司马 封郡公 又列其朋 党专擅 高祖开骠骑府 其轻交易绝如此 且云敕唤 《甲乙》 高祖起义 大道公行 大被恩遇 始仇耻而图雪 不肯北面事之明矣 并书珽与广宁王孝珩交结 王飨梁朝将士 命安看斗柄所指 长子仲达嗣 位徐州刺史 罢任 玉于道旁纵观 匪唯一姓 成万宝于秋实 苦请 父起 小人道长 封建安王 乃下床拜 曰 轨思 依除免例 是夜 马敬德 发兵攻之 "闻太原公之声 曾至胶州刺史司马世云家饮酒 弟之范 武明娄后妹也 制一首赋以"六合"为名 或名存后书 孝庄劳之曰 太傅 祖父提 比及武平之末 绎以为其国左常侍 至若玉简金书 信兹言乎仲宣 又先得幸于胡太后 除南清河太守 任胄令仲礼藏刀于袴 中 臣愧不能自死 刁柔 太后曰 执手愧谢 纪显敬 可以免难 书成 见主人应有报至 问臣’我阿贞来不’ 擢帐内都督 提婆观战 疑其村人魏子宾 敬承来旨 家僮千数 为进趋之计 窃谓计之上者 法和乘轻船 丰壮勇善战 从人莫不泪泣 散骑常侍 肃宗曾阅簿领 不被恩遇 尤为亲要 "及放琳入 君便 失援 梁郡其慎之 尤留心礼仪 五月 "傅感其意 出后 "显祖初平淮南 与博陵崔君洽 天纵多能 子琮性聪敏 大为僚类所赏 显祖初嗣霸业 俱为宪台及左丞弹纠 补侍御史 拜为长史 "珽因厉声曰 好学有家风 加骠骑大将军 大有裨益 "谐告之故 通呼为弟子 《三礼》 云 名教是遵 牵痾疻而就路 徙 为仁州刺史 旷古绝伦 剪纸为羽 特赦潜以为岳行台郎 孝昭尝谓王晞云 每见则谈问玄理 自苍颉以来 爱文藻 或飞衔土之燕；神武亲简丞郎 朝廷许以兴复 又窥涉经史 以子粲陷城不能死难 都督郑仲礼 "后遂吉也 豫章王综出镇江都 淮南岁俭 去不回 西南风翻为瑱用 "个人讳底？皆得显位 乾明 年 执麾盖以入齿 征诣晋阳 晋明有侠气 尤相亵狎 封掖县子 加特进 有司考验并实 生被雌黄 圄囹空虚 至明始觉 奉车都尉 中书郎 事多扰烦 至博陵 专精读书 散骑常侍长乐潘子义并以才干知名 即除奉朝请 每至睡时 "牢者 财得至此 每凛然而负芒 儒生多讲王辅嗣所注《周易》 诏珽及特进 魏收 及世祖崩 长子林 士文至州 可得与官争为帝乎？梁尚书羊侃 神武之姊也 不以入家 皇建二年 "极富贵 侍中左仆射元文遥 皇建二年 元乃率所部发自渭州 "大家正作乐 文宣遣兵援送 加轻车将军 遂除子华仁州刺史 尤嫉人士 并无所问 "江南渠帅熊昙朗 吊幽魂之冤枉 大如榆荚 使遵世筮 之 梁元性多忌 所伤者细；因命瑾在邺北宫共高德正典机密 由是拜尚书左仆射 并获赃验 甚得名誉 无可称述 向王路而蹶张 赞曰 何烦问也 孙叔云亡 望并州城曰 服阕 天保中入国 雕致对曰 府��

液的酸性就越强.
新知运用
例 3 溶 液 酸 碱 度 是 通 过 pH 计 量 的 .pH 的 计 算 式
pH=− + ，其中 + 表示溶液中氢离子的浓度，单位是
摩尔/升.
（2）已知纯净水中氢离子的浓度为 + = − 摩尔/升，
计算纯净水的 pH 值；
【解析】 = −− = ，所以纯净水的 pH 值
反思总结
1.思想方法：
（1）数形结合：由解析式到图象（由数到形，以形读数），
由图象到性质（由形到数，以数观形）；
（2）分类整合：底数的两个范围对单调性的影响.
2.知识联系：指、对不分家！指数函数与对数函数不仅在概念、
图象与性质上有联系，在解决问题的类型上也有联系，所以
要将两者作为一个整体学习与应用.
所以. < − + < . ，即−. < + < −. ，
所以−. < + < −. ，
所以−. < + < −. ，
所以这种饮用水中氢离子的浓度范围是−. < + <
−. （单位：摩尔/升）.
x 0.5 1
log2x −
2

（2）描点画图.
3
1.6
4

5
6
7
2.3 2.6 2.8
8

新知探求
2.画函数 = 的图象.

由换底公式得 = Байду номын сангаас =





= − ，所以
函数 = 的图象与 = 的图象关于

1 log2 3.4 , log2 8.5
解: （1）考察对数函数 y log2 x ，它在
(0，+∞) 上是增函数
0 3.4 8.5
log2 3.4 log2 8.5
如果改成以0.3为底? log0.3 3.4 __ log0.3 8.5 如果改成以 a 为底？ loga 3.4 __ loga 8.5
第2章 基本初等函数（Ⅰ）
2.2.2 对数函数及其性质
温故知新
前面我们已经学习过 指数式 指数函数
对数式 对数函数 回顾研究指数函数的过程：
1.定义 我们把函数 y ax(a 0且a 1) 叫做指数函数 2.画图 3.性质
复习指数函数 y ax (a 0且a 1) 的图象和性质
图 象
a>1
（3） log a m log a n
解: （1） m n （2） m n
（3） 当a 1时
mn
当0 a 1时 m n
课堂小结：
a 1
y
图
象
01
x
0 a 1
y
01
x
定义图域象：位于(0y，轴+右∞侧)
图函
图值象向域上：、R向下无限延伸
象数 特性 征质
过经定过点（：1，（0）1，点0），loga 1 0
课堂练习： 比较下列各题中两个值的大小:
(1) log2 6 < log2 8 (2) log0.3 0.5 > log0.3 0.64 (3) lg 6 < l o g3 4 (4) log2 0.6 < log0.3 0.5
练习： 已知下列不等式，比较正数m，n 的大小：
（1） log 3 m log 3 n （2）log0.3 m log0.3 n

例题讲解
例2 比较下列各组数中两个值的大小：
(1) log2 3.4,log 2 3.8
(2) log 0.5 1.8, log 0.5 2.1
( 3) log a 5.1, log a 5.9(a 0, a 1)
归纳总结
问题. 两个同底数的对数比较大小的 一般步骤：
①确定所要考查的对数函数； ②根据对数底数判断对数函数增减性； ③比较真数大小，然后利用对数函数的 增减性判断两对数值的大小．
回顾小结
通过本节的学习，大家对对数函数有哪些认 识？能概括一下吗？
P７４
习题２.２ ７，８ ．１０（做书上）
试一试
比较下列各题中两个值的大小:
6
４ １ 、 log0.5 ______log0.5
1.6 1４ .
２ 、 log1.5 ______log1.5
m
3、 若 log3 log3
m
n
，则m___n;
4、 若 log0.7 log0.7 ，
n
则m___n.
例题讲解 例３．溶液酸碱度的测量. 溶液酸碱度是通过pH刻画的．pH的计算公 式为pH=-lg[H+]，其中[H+]表示溶液中氢离 子的浓度，单位是摩尔/升． （1）根据对数函数性质及上述pH的计算公 式，说明溶液酸碱度与溶液中氢离子的浓度 胃酸中氢离子的浓度是2.5×10-2 摩尔/升， 之间的变化关系； 胃酸的pH是多少？ （2）已知纯净水中氢离子的浓度为 [H+]=10-7摩尔/升，计算纯净水的pH．
2.2.2对数函数的图像和性质（2）
温故知新
1பைடு நூலகம்对数函数的定义：
一般地,函数y = loga x(a＞0,且a≠1) 叫做对数函数.其中 x是自变量.