24.2 第1课时 配方法

人教版数学九年级上册21.2.2《配方法（1）》教学设计一. 教材分析《配方法（1）》是人教版数学九年级上册第21.2.2节的内容，主要讲述了配方法的基本概念和应用。

配方法是一种解决二次方程的有效方法，通过将二次方程转化为完全平方形式，从而简化计算和求解过程。

本节内容主要包括配方法的定义、配方法的步骤以及配方法在解决实际问题中的应用。

二. 学情分析九年级的学生已经掌握了二次方程的基本概念和求解方法，具备了一定的数学基础。

但学生在解决实际问题时，往往对这些方法的应用范围和条件把握不清，不能灵活运用。

因此，在教学本节内容时，需要帮助学生巩固已有的知识，并通过实例讲解和练习，让学生理解和掌握配方法的特点和应用。

三. 教学目标1.知识与技能：使学生理解配方法的基本概念和步骤，能够运用配方法解决简单的实际问题。

2.过程与方法：通过实例分析和练习，培养学生运用配方法解决问题的能力，提高学生的数学思维水平。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的自主学习能力和团队合作精神。

四. 教学重难点1.配方法的基本概念和步骤。

2.配方法在解决实际问题中的应用。

五. 教学方法1.讲授法：通过讲解配方法的基本概念和步骤，使学生掌握配方法的理论知识。

2.案例分析法：通过实例分析，让学生了解配方法在解决实际问题中的应用。

3.练习法：通过课堂练习和课后作业，巩固学生对配方法的理解和应用。

4.小组讨论法：鼓励学生分组讨论，培养学生的团队合作精神和数学思维能力。

六. 教学准备1.教材和教辅：准备人教版数学九年级上册教材和相关教辅资料。

2.课件和幻灯片：制作课件和幻灯片，用于课堂讲解和展示。

3.练习题和答案：准备一些配方法的练习题，并准备相应的答案。

七. 教学过程1.导入（5分钟）通过一个实际问题引入本节内容，例如：“某数加上其倒数的和为2，求这个数。

”让学生尝试解决此问题，引发学生对配方法的思考。

2.呈现（15分钟）讲解配方法的基本概念和步骤，并举例说明配方法在解决实际问题中的应用。

《配方法》教学设计
第1课时
一、教学目标
1.理解一元二次方程“降次”的转化思想，对形如(x+m)2=p(p≥0)的一元二次方程进行直
接开平方法求解；
2.掌握形如ax2+c=0和e(ax+m)2+n=p的一元二次方程的解法；
3.通过探究和学习直接开平方法的过程，使学生体会“换元”与“分类讨论”的数学思想；
4. 经历运用直接开平方法解一元二次方程的过程，使学生在学习中体会成功感，感受
数学学习的价值.
二、教学重难点
重点：用直接开平方法解一元二次方程.
难点：直接开方后得两个一元一次方程（降次思想）.
三、教学用具
多媒体等.
四、教学过程设计
【合作探究】
一桶油漆可刷的面积为1500 dm2，李林用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面，你能算出盒子的棱长吗？
解：设其中一个盒子的棱长为x dm，则这个盒子的表面积为_6x2__dm2，根据一桶油漆可刷的面积列出方程：_10×6x2=1500_，整理，得__x2=25___，根据平方根的意义，得x=_±5__，即x1=__5___，x2=__– 5____，经验证，_5____和__– 5____是方程的根，因为棱长不能是负值，所以盒子的棱长为__5____dm.
【合作探究】
教师活动：根据已经探究过的x2=25有两个根，再结合平方根的意义，总结出形如x2=p的方程的根的情况
以思维导图的形式呈现本节课所讲解的内容. 教科书。

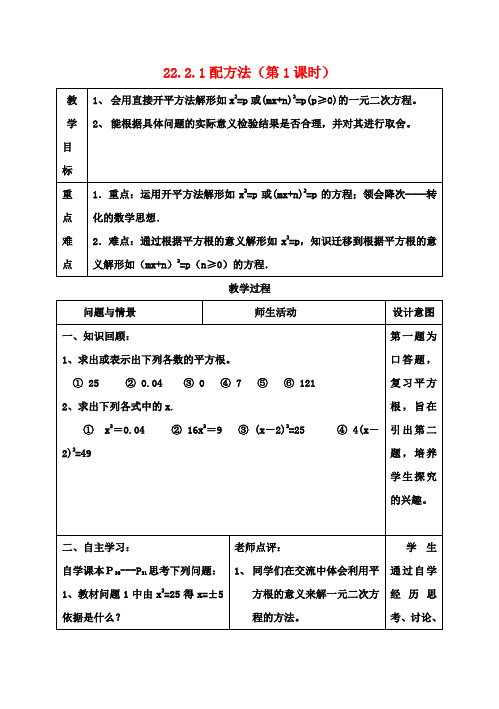
人教版数学九年级上册22.2.1《配方法》教案2一. 教材分析《配方法》是人教版数学九年级上册第22章第2节的一部分，主要介绍了配方法的概念、意义和应用。

配方法是解一元二次方程的一种方法，通过将方程转化为完全平方形式，使方程的解变得简单。

这一节的内容是学生学习一元二次方程解法的重要基础，也是后续学习二次函数和一元二次方程组的基础。

二. 学情分析九年级的学生已经具备了一定的代数基础，能够理解和运用一元一次方程、不等式的解法。

但是，对于一元二次方程，学生可能还存在一定的困难。

因此，在教学过程中，需要引导学生从已有的知识出发，逐步理解和掌握配方法。

三. 教学目标1.让学生理解配方法的概念和意义。

2.引导学生掌握配方法的操作步骤。

3.培养学生运用配方法解决实际问题的能力。

四. 教学重难点1.配方法的概念和意义的理解。

2.配方法的操作步骤的掌握。

五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。

通过设置问题，引导学生主动探究；通过案例分析，使学生理解配方法的实际应用；通过小组合作，培养学生的合作意识和团队精神。

六. 教学准备1.准备相关的教学案例和练习题。

2.准备教学PPT。

七. 教学过程1.导入（5分钟）利用PPT展示一些实际问题，引导学生思考如何解决这些问题。

例如，一个矩形的长比宽大3，已知矩形的面积为24，求矩形的长和宽。

2.呈现（10分钟）介绍配方法的概念和意义，讲解配方法的操作步骤。

通过PPT和案例，让学生直观地理解配方法的过程和效果。

3.操练（10分钟）让学生独立完成一些配方法的练习题。

在学生练习的过程中，教师进行个别辅导，解答学生的疑问。

4.巩固（10分钟）让学生分组讨论，总结配方法的操作步骤和注意事项。

每组派代表进行汇报，教师进行点评和总结。

5.拓展（10分钟）让学生运用配方法解决一些实际问题。

教师提供问题，学生分组讨论和解答。

6.小结（5分钟）教师引导学生总结本节课的主要内容和收获。

《配方法》教案及说课稿范文一、教学目标：知识与技能：1. 学生能够理解配方法的定义和意义。

2. 学生能够运用配方法解一元二次方程。

过程与方法：1. 学生通过自主探究和合作交流，掌握配方法的操作步骤。

2. 学生能够运用配方法解决实际问题，提高解决问题的能力。

情感态度与价值观：1. 学生培养对数学的兴趣和自信心，体验成功的喜悦。

2. 学生培养合作意识和团队精神，提高沟通能力。

二、教学重点与难点：重点：1. 配方法的定义和意义。

2. 配方法的操作步骤。

难点：1. 理解并掌握配方法的本质。

2. 灵活运用配方法解决实际问题。

三、教学准备：教师准备：1. 配方法的相关教学材料和案例。

2. PPT课件和教学道具。

学生准备：1. 预习配方法的相关知识。

2. 准备笔记本和文具。

四、教学过程：Step 1：导入新课1. 教师通过引入实际问题，引发学生对配方法的好奇心。

2. 学生听讲并思考问题。

Step 2：自主探究1. 教师给出配方法的定义和意义，引导学生自主探究。

2. 学生通过自学和小组讨论，理解并掌握配方法的操作步骤。

Step 3：合作交流1. 教师组织学生进行小组合作交流，分享各自的学习心得和解决问题的方法。

2. 学生积极参与讨论，提出问题和见解，互相学习和帮助。

Step 4：解决问题1. 教师给出实际问题，引导学生运用配方法解决。

2. 学生独立或合作运用配方法解决问题，展示解题过程和答案。

2. 学生分享自己的学习体会和感悟。

五、课后作业：1. 学生完成课后练习题，巩固所学知识。

教学反思：六、教学策略与方法：1. 实例教学：通过具体的案例，让学生直观地理解配方法的应用。

2. 问题驱动：引导学生思考和探索问题，激发学生的学习兴趣和动力。

3. 合作学习：鼓励学生之间的合作和交流，培养学生的团队合作能力和沟通能力。

4. 实践操作：让学生通过实际操作和解决问题，加深对配方法的理解和运用。

七、教学评价：1. 课堂参与度：观察学生在课堂上的参与程度和积极性。

24.2 解一元二次方程第1课时配方法学习目标：1.学会用直接开平方法解简单的一元二次方程.2.了解配方法解一元二次方程的解题步骤.学习重点：配方法的解一元二次方程的步骤.学习难点：用配方法解一元二次方程.一、知识链接1.36的平方根是_______,49的平方根是________.2.若x2=4,则x=_______;若2x2=1,则x=______.3. 根据完全平方公式填空：⑴x2＋6x＋9＝﹙﹚2 ⑵x2－8x＋16＝﹙﹚2⑶x2＋10x＋﹙﹚2＝﹙﹚2⑷x2－3x ＋﹙﹚2＝﹙﹚2二、新知预习3.试着解下列方程：（1）（x+1）2=4；把x+1看成一个整体，先由开平方得x+1=______,则x=_______.【自主归纳】形如x2=p(p≥0)或（mx+n）2=p(p≥0)的一元二次方程可利用平方根的定义用开平方的方法直接求解，这种解方程的方程叫做直接开平方法.（2）x2+2x-3=0.第一步：把常数项移到等式的右边，方程变形为x2+2x=_____第二步：等号两边同时加上一个常数，使等号左边成为一个完全平方形式：x2+2x+_____=______，（想一想，等号两边应同时加上几，依据是什么？）第三步：用直接开平方法解方程，（x+____）2=____.开平方可得x+____=±____.于是可以得到方程的解为________________.这样，我们就可以得到解方程x2+2x-3=0的一种方法：【自主归纳】像这种先对原一元二次方程配方,使它一边出现含未知数的一次式的平方后, 再用直接开平方求解的方法叫做配方法.三、自学自测1.解下列方程（1）(x-3)2＝9；（2）x2－2x+1＝0四、我的疑惑_____________________________________________________________________________合作探究一、要点探究探究点1：直接开平方法解一元二次方程如果方程能化成x2=p或(mx+n)2=p(p≥0)的形式，那么可得x=____,或mx+n=_______,即x=________.解一元二次方程的数学思想是“降次”，将一元二次方程转化为两个一元一次方程.【针对训练】1.方程x2－36＝0的解是( )A．x＝6 B．x＝－6 C．x＝4或9 D．x＝±62.解下列方程：（1）（x+2）2=36 （2）x2+6x+9=0.探究点2：用配方法解一元二次方程问题2：用配方法解二次项系数为1的一元二次方程例1：用配方法解下列方程：（1）x2-10x-11=0；（2）x2+2x-1=0.解：移项，得_____________________. 解：移项，得_____________________.配方，得______________________. 配方，得______________________.即____________________. 即____________________.两边开平方，得_____________. 两边开平方，得_____________.所以___________________. 所以___________________.例2：用配方法解：2x2+3=6x.解：移项，并将二次项系数化为1，得_____________.配方，得______________________.即____________________.两边开平方，得_____________.所以___________________.3.解下列方程：（1）y2-4y+2=0. （2）3x2-6x=1.二、课堂小结1.用配方法解方程x 2-2x-5=0时，原方程应变形为（ ） A.（x+1）2=6 B.（x-1）2=6 C.（x+2）2=9 D.（x-2）2=92.将方程x 2-6x+7化成（x+m ）2=k 的形式，则m 、k 的值分别是（ ） A.m=3，k=2 B.m=-3，k=-7 C.m=3，k=9 D.m=-3，k=2 3.用配方法解方程：（1）3x 2-27=0； （2）x 2+6x-7=0；（3）4x 2-2x-1=0； （4）21550.224x x +-=4.已知两个连续奇数的乘积是195，求这两个数的和.5.（拓展）用配方法证明：2x 2-8x+9恒为正.当堂检测参考答案： 1.B 2.D3.（1）123,3;x x ==- （2）121,7;x x ==-（3）121144x x +==（4）125522x x +== 4.设较小的一个奇数为x ，另一个为x+2，由题意，列方程得：x （x+2）=195，解得x=13或x=-15.所以这两个数的和为28或-28.。