对数运算及其对数函数

对数与对数函数 知识梳理1、对数式log a N 可看作一记号，表示底为a （a ＞0，且a ≠1），幂为N 的指数工表示方程xa N =（a ＞0，且a ≠1）的解. 也可以看作一种运算，即已知底为a （a ＞0，且a ≠1）幂为N ，求幂指数的运算. 因此，对数式log a N 又可看幂运算的逆运算.为a ＞0，a ≠1时，log x N a a N x =⇔= 【扩展】两类对数① 以10为底的对数称为常用对数，10log N 常记为lg N .② 以无理数e=2.71828…为底的对数称为自然对数，log e N 常记为ln N .以后解题时，在没有指出对数的底的情况下，都是指常用对数，如100的对数等于2，即lg1002=.说明：在例1中，10log 0.010.01,log 10ln10e 应改为lg 应改为. 2、对数的运算法则如果a ＞0且a ≠1，M ＞0，N ＞0，那么：（1）log log log a a a MN M N =+ （2）log log log aa a MM N N=- （3）log log ()n a a M n Mn R =∈3、画出函数2log xy =的图象, 再利用电脑软件画出0.5log .x y =的图象42-2-4-55探究：选取底数(a a ＞0，且a ≠1）的若干不同的值，在同一平面直角坐标系内作出相应的对数函数的图象．观察图象，你能发现它们有哪些特征吗？画出4log y x =，3log y x =，13log y x =和14log y x =提问：通过函数的图象，你能说出底数与函数图象的关系吗？函数的图象有何特征，性质又如何？先由学生讨论、交流，教师引导总结出函数的性质. (投影) 图象的特征函数的性质（1）图象都在y 轴的右边 （1）定义域是（0，+∞） （2）函数图象都经过（1，0）点 （2）1的对数是0（3）从左往右看，当a ＞1时，图象逐渐上升，当0＜a ＜1时，图象逐渐下降 .（3）当a ＞1时，log xa y =是增函数，当0＜a ＜1时，log a y x =是减函数. （4）当a ＞1时，函数图象在（1，0）点右边的纵坐标都大于0，在（1，0）点左边的纵坐标都小于0. 当0＜a ＜1时，图象正好相反，在（1，0）点右边的纵坐标都小于0，在（1，0）点左边的纵坐标都大于0 .（4）当a ＞1时x ＞1，则log a x ＞00＜x ＜1，log a x ＜0 当0＜a ＜1时x ＞1，则log a x ＜00＜x ＜1，log a x ＜0由上述表格可知，对数函数的性质如下（先由学生仿造指数函数性质完成，教师适当启发、引导）：a ＞10＜a ＜1图象性 质（1）定义域（0，+∞）； （2）值域R ； （3）过点（1，0），即当x =1，y =0； （4）在（0，+∞）上是增函数在（0，+∞）是上减函数精讲精练（1）对数运算的例题【例1】将下列指数式化为对数式，对数式化为指数式：（1）712128-=； （2）327a =； （3）1100.1-=；（4）12log 325=-； （5）lg0.0013=-； （6）ln100=4.606.【例2】求证：（1）log n a a n =； （2）log log log a a a MM N N-=.【例3】试推导出换底公式：log log log c a c bb a= （0a >，且1a ≠；0c >，且1c ≠；0b >）.【例4】化简与求值：（1）221(lg 2)lg2lg5(lg 2)lg212++-+ ；（2）2log (4747)++-.【例5】若2510a b ==，则11a b+= . （教材P 83 B 组2题） 【例6】 （1）方程lg lg(3)1x x ++=的解x =________；（2）设12,x x 是方程2lg lg 0x a x b ++=的两个根，则12x x 的值是 .【例7】（1）化简：532111log 7log 7log 7++；（2）设23420052006log 3log 4log 5log 2006log 4m ⋅⋅⋅= ，求实数m 的值.（2）对数函数图象和性质的例题【例1】比较大小：（1）0.9log 0.8，0.9log 0.7，0.8log 0.9； （2）3log 2，2log 3，41log 3.【例2】求下列函数的定义域：（1）2log (35)y x =-；（2）0.5log (4)3y x =-.【例3】已知函数()log (3)a f x x =+的区间[2,1]--上总有|()|2f x <，求实数a 的取值范围.【例4】求不等式log (27)log (41)(0,1)a a x x a a +>->≠且中x 的取值范围.【例5】讨论函数0.3log (32)y x =-的单调性.【例6】（05年山东卷.文2）下列大小关系正确的是（ ）. A. 30.440.43log 0.3<< B. 30.440.4log 0.33<< C. 30.44log 0.30.43<< D. 0.434log 0.330.4<<【例7】指数函数(0,1)x y a a a =>≠的图象与对数函数log (0,1)a y x a a =>≠的图象有何关系？课堂作业（1）对数幂的运算1. 将下列指数式与对数式互化，有x 的求出x 的值 .（1）12155-=（2）42log x = （3）1327x =（4）1()644x= （5）lg0.0001x = （6）5ln e x =2．求log log log ,a b c b c Na⋅⋅∈+的值(a,b,c R 且不等于1，N ＞0）.3．计算331log log 5533+的值.4、判断下列式子是否正确，a ＞0且a ≠1，x ＞0且a ≠1，x ＞0，x ＞y ，则有（1）log log log ()a a a x y x y ⋅=+ （2）log log log ()a a a x y x y -=-（3）log log log aa a xx y y=÷ （4）log log log a a a xy x y =- （5）(log )log n a a x n x = （6）1log log a a x x=- （7）1log log n a a x x n=5. 用log a x ，log a y ，log a z 表示出（1）（2）小题，并求出（3）、（4）小题的值.（1）log a xyz =____________; （2）23log 8a x y =______________________;（3）75log (42)z ⨯=______________; （4）5lg 100=_____________________; 6. 已知32a=，那么33log 82log 6-用a 表示是（ ）A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a - 7、2log (2)log log a a a M N M N -=+，则NM的值为（ ） A 、41B 、4C 、1D 、4或1 8、已知221,0,0x y x y +=>>，且1log (1),log ,log 1y a a a x m n x+==-则等于（ ）A 、m n +B 、m n -C 、()12m n +D 、()12m n -9、如果方程2lg (lg5lg7)lg lg5lg70x x +++= 的两根是,αβ，则αβ 的值是（ ）A 、lg5lg 7B 、lg 35C 、35D 、351 10、已知732log [log (log )]0x =，那么12x -等于（ ）A 、13 B 、123 C 、122 D 、13311. 若2log 2,log 3,m n a a m n a +=== 。

§2.2.1 对数与对数运算（一）¤知识要点：1. 定义：一般地，如果x a N =(0,1)a a >≠，那么数 x 叫做以a 为底 N 的对数（logarithm ）.记作 log a x N =，其中a 叫做对数的底数，N 叫做真数2. 我们通常将以10为底的对数叫做常用对数（common logarithm ），并把常用对数10log N 简记为lg N 在科学技术中常使用以无理数e=2.71828……为底的对数，以e 为底的对数叫自然对数，并把自然对数log e N 简记作ln N3. 根据对数的定义，得到对数与指数间的互化关系：当0,1a a >≠时，log b a N b a N =⇔=.4. 负数与零没有对数；log 10a =， log 1a a = ，log a a N N = ¤例题精讲：【例1】将下列指数式化为对数式，对数式化为指数式：（1）712128-=； （2）327a =； （3）1100.1-=； （4）12log 325=-； （5）lg0.0013=-； （6）ln100=4.606.【例2】计算下列各式的值：（1）lg0.001； （2）4log 8； （3）.第14练 §2.2.1 对数与对数运算（一）※基础达标1．log (0,1,0)b N a b b N =>≠>对应的指数式是（ ）. A. b a N = B. a b N = C. N a b = D. N b a = 2．下列指数式与对数式互化不正确的一组是（ ）. A. 01ln10e ==与 B. 1()381118log 223-==-与 C. 123log 9293==与 D. 17log 7177==与 3．设lg 525x =，则x 的值等于（ ）.A. 10B. 0.01C. 100D. 10004．设13log 82x=，则底数x 的值等于（ ）. A. 2 B. 12 C. 4 D. 145．已知432log [log (log )]0x =，那么12x -等于（ ）.A.13 B. C. D. 6．若21log 3x =，则x = ； 若log 32x =-，则x = .7．计算：= ； 6lg 0.1= .※能力提高8．求下列各式的值：（1）8； （2）9log9．求下列各式中x 的取值范围：（1）1log (3)x x -+； （2）12log (32)x x -+.※探究创新10．（1）设log 2a m =，log 3a n =，求2m n a +的值.（2）设{0,1,2}A =,{log 1,log 2,}a a B a =，且A B =，求a 的值.第15讲 §2.2.1 对数与对数运算（二）¤知识要点：1. 对数的运算法则：log ()log log a a a M N M N =+，log log log aa a MM N N=-，log log n a a M n M =，其中0,1a a >≠且，0,0,M N n R >>∈. 三条法则是有力的解题工具，能化简与求值复杂的对数式.2. 对数的换底公式log log log b a b N N a =. 如果令b =N ，则得到了对数的倒数公式1log log a b b a=. 同样，也可以推导出一些对数恒等式，如log log n n a a N N =，log log m n a a nN N m=，log log log 1a b c b c a =等. ¤例题精讲：【例2】若2510a b ==，则11a b+= .【例4】（1）化简：532111log 7log 7log 7++； （2）设23420052006log 3log 4log 5log 2006log 4m ⋅⋅⋅=，求实数m 的值.第15练 §2.2.1 对数与对数运算（二）※基础达标 1．）. A. 1B. －1C. 2D. －2 2．25log ()a -（a ≠0）化简得结果是（ ）.A. －aB. a 2C. ｜a ｜D. a3．化简3log 1的结果是（ ）. A.12B. 1C. 24．已知32()log f x x =, 则(8)f 的值等于（ ）. A. 1 B. 2 C. 8 D. 125．化简3458log 4log 5log 8log 9⋅⋅⋅的结果是 （ ）.A .1 B.32C. 2D.3 6．计算2(lg5)lg 2lg50+⋅＝ .7．若3a ＝2，则log 38－2log 36＝ .第16讲 §2.2.2 对数函数及其性质（一）¤知识要点：1. 定义：一般地，当a ＞0且a ≠1时，函数a y=log x 叫做对数函数(logarithmic function). 自变量是x ； 函数的定义域是（0，+∞）.2. 由2log y x =与12log y x =的图象，可以归纳出对数函数的性质：定义域为(0,)+∞，值域为R ；当1x =时，0y =，即图象过定点(1,0)；当01a <<时，在(0,)+∞上递减，当1a >时，在(0,)+∞上递增.¤例题精讲：【例1】比较大小：（1）0.9log 0.8，0.9log 0.7，0.8log 0.9； （2）3log 2，2log 3，41log 3.【例2】求下列函数的定义域：（1）y =（2）y =【例4】求不等式log (27)log (41)(0,1)a a x x a a +>->≠且中x 的取值范围.第16练 §2.2.2 对数函数及其性质（一）※基础达标1．下列各式错误的是（ ）.A. 0.80.733>B. 0.10.10.750.75-<C. 0..50..5log 0.4log 0.6>D. lg1.6lg1.4>.2．当01a <<时,在同一坐标系中,函数log x a y a y x -==与的图象是（ ）.AC3．下列函数中哪个与函数y =x 是同一个函数（ ）A.log (0,1)a xy aa a =>≠ B. y =2x xC. log (0,1)x a y a a a =>≠D. y4．函数y ）.A. (1,)+∞B. (,2)-∞C. (2,)+∞D. (1,2] 5．若log 9log 90m n <<，那么,m n 满足的条件是（ ）.A. 1 m n >>B. 1n m >>C. 01n m <<<D. 01m n <<<6．函数y = . （用区间表示）7．比较两个对数值的大小：ln7 ln12 ； 0.5log 0.7 0.5log 0.8. ※能力提高8．求下列函数的定义域：（1） ()()3log 1f x x =++； （2）y =9．已知函数2()3log ,[1,4]f x x x =+∈，22()()[()]g x f x f x =-，求： （1）()f x 的值域； （2）()g x 的最大值及相应x 的值.第17讲 §2.2.2 对数函数及其性质（二）¤知识要点：1. 当一个函数是一一映射时, 可以把这个函数的因变量作为一个新函数的自变量, 而把这个函数的自变量新的函数的因变量. 我们称这两个函数为反函数（inverse function ）. 互为反函数的两个函数的图象关于直线y x =对称.2. 函数(0,1)x y a a a =>≠与对数函数log (0,1)a y x a a =>≠互为反函数.3. 复合函数(())y f x ϕ=的单调性研究，口诀是“同增异减”，即两个函数同增或同减，复合后结果为增函数；若两个函数一增一减，则复合后结果为减函数. 研究复合函数单调性的具体步骤是：（i ）求定义域；（ii ）拆分函数；（iii ）分别求(),()y f u u x ϕ==的单调性；（iv ）按“同增异减”得出复合函数的单调性.¤例题精讲：【例1】讨论函数0.3log (32)y x =-的单调性.【例2】（05年山东卷.文2）下列大小关系正确的是（ ）. A. 30.440.43log 0.3<< B. 30.440.4log 0.33<< C. 30.44log 0.30.43<< D. 0.434log 0.330.4<<第17练 §2.2.2 对数函数及其性质（二）※基础达标 1．函数1lg1xy x+=－的图象关于（ ）. A. y 轴对称 B. x 轴对称 C. 原点对称D. 直线y ＝x 对称2．函数212log (617)y x x =-+的值域是（ ）.A. RB. [8,)+∞C. (,3]-∞-D. [3,)+∞3．（07年全国卷.文理8）设1a >，函数()log a f x x =在区间[]2a a ，上的最大值与最小值之差为12，则a =（ ）.A.2B. 2C. 22D. 44．图中的曲线是log a y x =的图象，已知a 的值为2，43，310，15，则相应曲线1234,,,C C C C 的a 依次为（ ）.A.2，43，15，310 B. 2，43，310，15 C. 15，310，43，2 D. 43，2，310，155．下列函数中，在(0,2)上为增函数的是（ ）. A. 12log (1)y x =+ B. 22log 1y x =- C. 21log y x= D.20.2log (4)y x =-6． 函数2()lg(1)f x x x =+-是 函数. （填“奇”、“偶”或“非奇非偶”）7．函数x y a =的反函数的图象过点(9,2)，则a 的值为 . ※能力提高8．已知6()log ,(0,1)a f x a a x b=>≠-，讨论()f x 的单调性.0 x C 1C 2C 4C 3 1y第18讲 §2.3 幂函数¤学习目标：通过实例，了解幂函数的概念；结合函数y=x, y=x 2, y=x 3, y =1/x , y=x 1/2 的图像，了解它们的变化情况.知识要点：1. 幂函数的基本形式是y x α=，其中x 是自变量，α是常数. 要求掌握y x =，2y x =，3y x =，1/2y x =，1y x -=这五个常用幂函数的图象. 2. 观察出幂函数的共性，总结如下：（1）当0α>时，图象过定点(0,0),(1,1)；在(0,)+∞上是增函数.（2）当0α<时，图象过定点(1,1)；在(0,)+∞上是减函数；在第一象限内，图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象，在第一象限内，直线1x =的右侧，图象由下至上，指数α由小到大. y 轴和直线1x =之间，图象由上至下，指数α由小到大.¤例题精讲：【例1】已知幂函数()y f x =的图象过点(27,3)，试讨论其单调性.解：设y x α=，代入点(27,3)，得327α=，解得13α=，所以13y x =，在R 上单调递增.【例2】已知幂函数6()m y x m Z -=∈与2()m y x m Z -=∈的图象都与x 、y 轴都没有公共点，且2()m y x m Z -=∈的图象关于y 轴对称，求m 的值．解：∵ 幂函数图象与x 、y 轴都没有公共点，∴{6020m m -<-<，解得26m <<.又 ∵ 2()m y x m Z -=∈的图象关于y 轴对称， ∴ 2m -为偶数，即得4m =. 【例3】幂函数m y x =与n y x =在第一象限内的图象如图所示，则（ ）. A ．101n m -<<<< B ．1,01n m <-<< C ．10,1n m -<<> D ．1,1n m <->解：由幂函数图象在第一象限内的分布规律，观察第一象限内直线1x =的右侧，图象由下至上，依次是n y x =，1y x -=，0y x =，m y x =，1y x =，所以有101n m <-<<<. 选B.点评：观察第一象限内直线1x =的右侧，结合所记忆的分布规律. 注意比较两个隐含的图象1y x =与0y x =.【例4】本市某区大力开展民心工程，近几年来对全区2a m 的老房子进行平改坡（“平改坡”是指在建筑结构许可条件下，将多层住宅平屋面改建成坡屋顶，并对外墙面进行整修粉饰，达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为），且每年平改坡面积的百分比相等. 若改造到面积的一半时，所用时间需10年. 已知到今年为止，平改坡剩余面积为原来的22. （1）求每年平改坡的百分比；（2）问到今年为止，该平改坡工程已进行了多少年？ （3）若通过技术创新，至少保留24a m 的老房子开辟新的改造途径. 今后最多还需平改坡多少年？ 解：（1）设每年平改坡的百分比为(01)x x <<，则101(1)2a x a -=，即11011()2x -=，解得11011()0.0670 6.702x =-≈=%.（2）设到今年为止，该工程已经进行了n 年，则2(1)2na x a -=，即110211()()22n=，解得n =5.所以，到今年为止，该工程已经进行了5年.（3）设今后最多还需平改坡m 年，则 51(1)4m a x a +-=，即521011()()22m +=，解得m =15. 所以，今后最多还需平改坡15年.点评：以房屋改造为背景，从中抽象出函数模型，结合两组改造数据及要求，通过三个等式求得具有实际意义的底数或指数. 体现了代入法、方程思想等数学方法的运用.第18练 §2.3 幂函数※基础达标1．如果幂函数()f x x α=的图象经过点2(2,)2，则(4)f 的值等于（ ）. A. 16 B. 2 C. 116 D. 122．下列函数在区间(0,3)上是增函数的是（ ）.A. 1y x =B. 12y x = C. 1()3x y = D. 2215y x x =--3．设120.7a =，120.8b =，c 3log 0.7=，则（ ）.A. c <b <aB. c <a <bC. a <b <cD. b <a <c4．如图的曲线是幂函数n y x =在第一象限内的图象. 已知n 分别取2±，12±四个值，与曲线1c 、2c 、3c 、4c 相应的n 依次为（ ）.A ．112,,,222-- B. 112,,2,22--C. 11,2,2,22--D. 112,,,222--5．下列幂函数中过点(0,0)，(1,1)的偶函数是（ ）.A.12y x =B. 4y x =C. 2y x -=D.13y x = 6．幂函数()y f x =的图象过点1(4,)2，则(8)f 的值为 . 7．比较下列各组数的大小： 32(2)a + 32a ； 223(5)a -+ 235-； 0.50.4 0.40.5.※能力提高8．幂函数273235()(1)t t f x t t x +-=-+是偶函数，且在(0,)+∞上为增函数，求函数解析式.9．1992年底世界人口达到54.8亿，若人口的平均增长率为x %，2008年底世界人口数为y （亿）.（1）写出1993年底、1994年底、2000年底的世界人口数； （2）求2008年底的世界人口数y 与x 的函数解析式. 如果要使2008年的人口数不超过66.8亿，试求人口的年平均增长率应控制在多少以内？※探究创新4251c 4c 3c 2c 110．请把相应的幂函数图象代号填入表格.① 23y x =； ② 2y x -=；③ 12y x =； ④ 1y x -=； ⑤ 13y x =；⑥ 43y x =；⑦ 12y x -=；⑧ 53y x =. 第19讲 第二章 基本初等函数（Ⅰ） 复习¤学习目标：理解掌握指数函数、对数函数和幂函数的性质、图象及运算性质. 突出联系与转化、分类与讨论、数与形结合等重要的数学思想、能力. 通过对指数函数、对数函数等具体函数的研究，加深对函数概念的理解.¤例题精讲：【例1】若()(0,1)x f x a a a =>≠且，则1212()()()22x x f x f x f ++≤. 证明：121212122()()()222x x x x f x f x x x a a f a++++-=-0==≥. ∴ 1212()()()22x x f x f x f ++≤. （注：此性质为函数的凹凸性） 【例2】已知函数2()(0,0)1bxf x b a ax =≠>+.（1）判断()f x 的奇偶性； （2）若3211(1),log (4)log 422f a b =-=，求a ，b 的值.解：（1）()f x 定义域为R ，2()()1bxf x f x ax --==-+，故()f x 是奇函数.（2）由1(1)12b f a ==+，则210a b -+=.又log 3(4a -b )=1，即4a -b =3.由{21043a b a b -+=-=得a =1，b =1.【例3】（01天津卷.19）设a ＞0， ()x xe af x a e =+是R 上的偶函数.（1）求a 的值； （2）证明()f x 在(0,)+∞上是增函数．解：（1）∵ ()x xe af x a e =+是R 上的偶函数，∴ ()()0f x f x --=.∴ 110()()x x x x x x e a e a a e a e a e a e a a ---+--=⇒-+-10()()0x x a e e a-=⇒--=.e x －e -x 不可能恒为“0”， ∴ 当1a－a ＝0时等式恒成立， ∴a ＝1．（2）在(0,)+∞上任取x 1＜x 2，1212121212111()()()()x x x x x x x x e f x f x e e e a e e e e -=+--=-+-12121()(1)x x x x e e e e =--∵ e ＞1，x 1＜x 2， ∴ 121x x e e >>， ∴12x x e e ＞1，121212()(1)x x x x x x e e e e e e --＜0，∴ 12()()0f x f x -<， ∴ ()f x 是在(0,)+∞上的增函数．点评：本题主要考查了函数的奇偶性以及单调性的基础知识．此题中的函数，也可以看成指数函数xy a =与x a y a x =+的复合，可以进一步变式探讨x ay a x=+的单调性. 【例4】已知1992年底世界人口达到54.8亿.（1）若人口的平均增长率为1.2%，写出经过t 年后的世界人口数y （亿）与t 的函数解析式；（2）若人口的平均增长率为x %，写出2010年底世界人口数为y （亿）与x 的函数解析式. 如果要使2010年的人口数不超过66.8亿，试求人口的年平均增长率应控制在多少以内？解：（1）经过t 年后的世界人口数为 *54.8(1 1.2)54.8 1.012,t t y t N =⨯+%=⨯∈.（2）2010年底的世界人口数y 与x 的函数解析式为 1854.8(1)y x =⨯+%. 由1854.8(1)y x =⨯+%≤66.8， 解得1866.8100(1) 1.154.8x ≤⨯-≈. 所以，人口的年平均增长率应控制在1.1%以内.点评：解应用题应先建立数学模型，再用数学知识解决，然后回到实际问题，给出答案. 此题由增长率的知识，可以得到指数型或幂型函数，并得到关于增长率的简单不等式，解决实际中增长率控制问题.第19练 第二章 基本初等函数（Ⅰ） 复习※基础达标 1．（06年全国卷II.文2理1）已知集合{}2{|3},|log 1M x x N x x =<=>，则M N =（ ）.A. ∅B. {}|03x x <<C. {}|13x x <<D. {}|23x x << 2．（08年北京卷.文2）若372log πlog 6log 0.8a b c ===，，，则（ ）.A. a b c >>B. b a c >>C. c a b >>D. b c a >>3.（05年福建卷）函数()x b f x a -=的图象如图，其中a 、b 为常数，则下列结论正确的是（ ）. A. 1,0a b >< B. 1,0a b >> C. 01,0a b <<> D. 01,0a b <<<4．（06年广东卷）函数23()lg(31)1x f x x x=++-的定义域是（ ）.A.1(,)3-+∞B. 1(,1)3-C. 11(,)33-D. 1(,)3-∞-5．（06年陕西卷）设函数()log ()(0,1)a f x x b a a =+>≠的图像过点(2,1)，其反函数的图像过点(2,8)，则a b +等于（ ）.A. 3B. 4C. 5D. 66．（06年辽宁卷.文14理13）设,0(),0x e x g x lnx x ⎧≤=⎨>⎩，则1(())2g g = .7．如图所示，曲线是幂函数y x α=在第一象限内的图象，已知α分别取11,1,,22-四个值，则相应图象依次为 .※能力提高8．已知定义域为R 的函数12()2x x bf x a+-+=+是奇函数. 求,a b 的值.9．已知函数y =24log log 42x x(2≤x ≤4). （1）求输入x =234时对应的y 值； （2）令2log t x =，求y 关于t 的函数关系式及t 的范围.※探究创新10．设121()log 1axf x x -=-为奇函数，a 为常数. （1）求a 的值； （2）证明()f x 在区间（1，＋∞）内单调递增；（3）若对于区间[3,4]上的每一个x 值，不等式()f x >1()2x m +恒成立，求实数m 的取值范围．。

对数运算与对数函数在数学的广袤世界里，对数运算与对数函数就像隐藏在迷雾中的神秘宝藏，等待着我们去探索和发现。

它们不仅是数学理论中的重要组成部分，更在实际生活和科学研究中有着广泛而深刻的应用。

让我们先从对数运算说起。

对数运算其实就是一种数学运算方式，它是指数运算的逆运算。

想象一下，如果有一个等式 a^b ＝ N，那么对数运算就是要找出 b 的值，我们记为logₐN ＝ b。

比如说，2³＝ 8，那么 log₂8 ＝ 3。

这就像是在解一个谜题，已知结果和底数，要找出指数。

为什么要有对数运算呢？这是因为在很多实际问题中，直接处理指数形式的数量关系可能会非常困难，但通过对数运算，就能将复杂的问题简单化。

例如，在测量声音强度时，我们使用的单位是分贝（dB），而分贝的计算就涉及到对数运算。

再来说说对数的一些基本性质。

首先是对数的乘法法则：logₐ(MN) ＝logₐM ＋logₐN。

这意味着，如果要计算两个数的乘积的对数，就可以转化为这两个数的对数的和。

同样，还有除法法则：logₐ(M/N) ＝logₐM logₐN。

而对数函数则是基于对数运算构建起来的一类函数。

常见的对数函数形式为 y ＝logₐx，其中 a 被称为底数，且 a ＞ 0 且a ≠ 1。

当 a ＞ 1时，对数函数是单调递增的；当 0 ＜ a ＜ 1 时，对数函数是单调递减的。

对数函数的图像具有一些独特的特征。

以底数 a ＞ 1 为例，函数图像经过点(1, 0)，并且逐渐向右上方延伸，越来越陡峭。

而当 0 ＜ a ＜1 时，图像经过点(1, 0)，逐渐向右下方延伸，变得越来越平缓。

对数函数在解决实际问题中发挥着巨大的作用。

比如在金融学中，计算复利增长；在物理学中，描述某些自然现象的变化规律；在计算机科学中，分析算法的时间复杂度等等。

举个简单的例子，假设你在银行存了一笔钱，年利率为 r，经过 t年后，本金和利息的总和 A 与初始本金 P 之间的关系可以表示为 A ＝P(1 ＋ r)＾t。

对数的计算以及对数函数的基本性质1.对数与对数运算 （1）对数的定义①若(0,1)xa N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N=，其中a 叫做底数，N 叫做真数．②负数和零没有对数． ③对数式与指数式的互化：log (0,1,0)x a x N a N a a N =⇔=>≠>．（2）几个重要的对数恒等式：log 10a =，log 1a a =，log ba ab =． （3）常用对数与自然对数 常用对数：lg N ，即10log N； 自然对数：ln N ，即log e N（其中 2.71828e =…）．（4）对数的运算性质如果0,1,0,0a a M N >≠>>，那么 ①加法：log log log ()a a a M N MN += ②减法：log log log a a aMM N N-= ③数乘：log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b N N b b a =>≠且 2.对数函数及其性质 定义：函数log (0a y x a =>且1)a ≠叫做对数函数图象：定义域：(0,)+∞ 值域：R 过定点：图象过定点(1,0)，即当1x =时，0y =．1 xy O1xyO奇偶性：非奇非偶 单调性：在(0,)+∞上是增函数1a >；在(0,)+∞上是减函数01a <<； 函数值的变化情况：log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<变化对图象的影响：在第一象限内，a 越大图象越靠低；在第四象限内，a 越大图象越靠高． 判断技巧：指数函数令1=x 得到第一象限内底大图上；对数函数令1=y 得到第一象限底大图下。

1.对数的概念如果 ,那么数b 叫做以a 为底N 的对数，记作 ，其中a 叫做对数的 ，N 叫做对数的 。

即指数式与对数式的互化：log ba aN b N =⇔=2.常用对数：通常将以10为底的对数10log N 叫做常用对数，记作lg N 。

自然对数：通常将以无理数 2.71828e =⋅⋅⋅为底的对数叫做自然对数，记作ln N 。

3．对数的运算性质：如果0a >，且1,0,0a M N ≠>>，那么：⑴log ()log log a a a M N M N ⋅=+；（积的对数等于对数的和） 推广1212log (...)log log ...log a k a a a k N N N N N N ⋅=+++ ⑵log log log aa a MM N N=-；（商的对数等于对数的差） ⑶log log (R)a a M M ααα=∈，则log a = 。

⑷log a N a N =2．换底公式：log log log a b a NN b=（,0,,1,0a b a b N >≠>） 换底公式的意义：把以一个数为底的对数换成以另一个大于0且不等于1的数为底的对数，以达到计算、化简或证明的目的． 推广：⑴1log log a b b a=⑵log log log log a b c a b c d d =， ⑶1log log n a a M M n =，则log na m M = 。

特别地：log log 1a b b a =知识要点对数运算与对数函数【例1】 求下列各式中x 的取值范围。

（1）2log (5)x +（2）1log (10)x x --【例2】 将下列指数式化为对数式，对数式化为指数式。

（1） 1642= （2） 9132=- （3） 481log 3=（4） 6125log -=a （5）lg0.0013=-； （6）ln100=4.606【例3】 计算（1）lg 4lg 25+ （2）22log 24log 6-（3）531log ()3（4） 001.0lg （5）e1ln （6）1lg【巩固1】3log =2log =(2log (2= 21log 52+=【巩固2】）. A. 1 B. －1 C. 2 D. －2【巩固3】计算2(lg5)lg 2lg50+⋅＝ .知识要点【例4】 （1）（2 。

对数与对数函数一、相关知识点1.对数的定义：如果()1,0≠>=a a N a x 且，那么数x 叫做以a 为底，N 的对数，记作N x a log =，其中a 叫做对数的底数，N 叫做真数。

2.几种常见对数(1)()1,0≠>a a 且①01log =a ; ②1log =a a ; ③N a Na =log ; ④N a N a =log .（两个对数恒等式） (2)对数的重要公式：①换底公式：()0,1,log log log >=N b a b aN aNb均为大于零且不等于；②abba log 1log =，推广：da d c cb b a log log log log =⋅⋅. （3）对数的运算法则：如果0,0,1,0>>≠>N M a a 且，那么 ①()Na M a MN aloglog log += ; ②NaM a N Malog log log -=； ③()R n n MaM a n∈=log log ；④b a b a mnnm log log = . 3.反函数，只需了解：指数函数xa y =与对数函数xa y log =互为反函数，它们的图象关于直线x y =对称。

题型一：对数的化简和求值1.计算:(1)2110025lg 41lg ÷⎪⎭⎫ ⎝⎛-；(2)32log 2450lg 2lg 5lg +⋅+；(3)()232031027.0252lg 3.0lg 21000lg 8lg 27lg --⎪⎭⎫⎝⎛-⨯+-++-+；(4)()222lg 20lg 5lg 8lg 325lg +++. 2.已知()[]0lg log log 25=x ，求x 的值.3.已知0>a ，且1≠a ，m a =2log ，n a =3log ，求nm a +2的值能力提高：(1).设m ba==52，且211=+ba ,则=m ; (2).若632==b a ，求证：c b a 111=+题型二：（1）对数函数的基本性质题型一：基本性质1.函数()()223lg +-=x x f 恒过定点_______________________2.如果0log log 2121<<y x ，那么（）(A)1<<x y ； (B)1<<y x ；(C)y x <<1； (D)x y <<1.3.已知()x x f a log =，()x x g b log =，()x x r c log =，()x x h d log =的图象如图所示则a ,b ,c ,d 的大小为A.b a d c <<<;B.a b d c <<<;C.b a c d <<<;D.d c b a <<<4.若函数()⎪⎩⎪⎨⎧<⎪⎭⎫⎝⎛+≥=）（）（4214log 2x x f x x x f ,则⎪⎭⎫⎝⎛23f 的值是( ) A.21; B.1; C.23; D.2 5.若点()b a ,在x y lg =图像上,1≠a ,则下列点也在此图像上的是（）A.⎪⎭⎫⎝⎛b a ,1;B. ()b a -1,10;C.⎪⎭⎫⎝⎛+1,10b a ; D.()b a 2,2. 6.函数()()13log 2+=xx f 的值域为7.为了得到函数103lg+=x y 的图像,只需把函数x y lg =的图像上所有的点( ) A.向左平移3个单位长度,再向上平移1个单位长度； B.向右平移3个单位长度,再向上平移1个单位长度； C.向左平移3个单位长度,再向下平移1个单位长度； D.向右平移3个单位长度,再向下平移1个单位长度.8.若函数()()()101≠>--=a a a a k x f xx且在R 上既是奇函数,又是减函数()()k x x g a +=log 的图象是( )9.对于函数()x f 定义域中任意的()2121,x x x x ≠，有如下结论： ①()()()2121x f x f x x f ⋅=+； ②()()()2121x f x f x x f +=⋅; ③()()02121>--x x x f x f ； ④()()222121x f x f x x f +<⎪⎭⎫ ⎝⎛+. 当()x x f lg =时，上述结论中正确结论的序号是. 能力提高：1.已知函数()22log 21+-=a y x 的值域是R ，求a 的取值范围.2.已知函数()()1log 22++=ax ax x f 的定义域为全体实数，求a 的取值范围.3.已知函数()()1log 22++=ax axx f 的值域域为全体实数，求a 的取值范围。

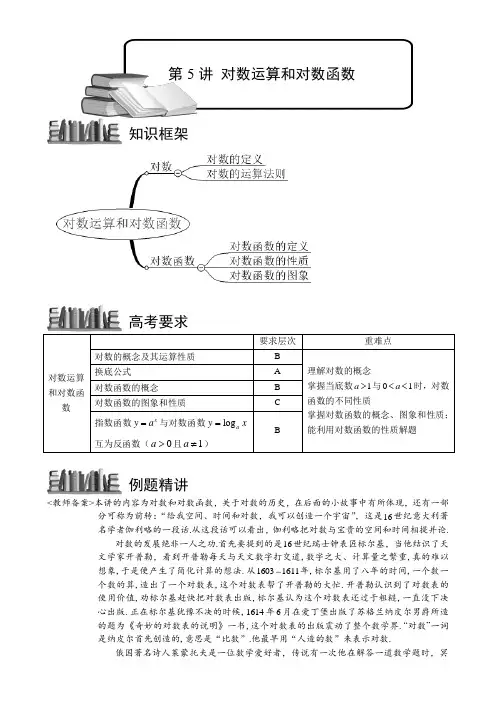
对数运算和对数函数要求层次重难点对数的概念及其运算性质B 理解对数的概念掌握当底数1a >与01a <<时，对数函数的不同性质掌握对数函数的概念、图象和性质；能利用对数函数的性质解题换底公式 A 对数函数的概念 B 对数函数的图象和性质C 指数函数xy a =与对数函数log a y x =互为反函数（0a >且1a ≠）B<教师备案>本讲的内容为对数和对数函数，关于对数的历史，在后面的小故事中有所体现，还有一部分可称为前转：“给我空间、时间和对数，我可以创造一个宇宙”，这是16世纪意大利著名学者伽利略的一段话.从这段话可以看出，伽利略把对数与宝贵的空间和时间相提并论.对数的发展绝非一人之功.首先要提到的是16世纪瑞士钟表匠标尔基，当他结识了天文学家开普勒，看到开普勒每天与天文数字打交道,数字之大、计算量之繁重,真的难以想象,于是便产生了简化计算的想法.从16031611年,标尔基用了八年的时间,一个数一个数的算,造出了一个对数表,这个对数表帮了开普勒的大忙.开普勒认识到了对数表的使用价值,劝标尔基赶快把对数表出版,标尔基认为这个对数表还过于粗糙,一直没下决心出版.正在标尔基犹豫不决的时候,1614年6月在爱丁堡出版了苏格兰纳皮尔男爵所造的题为《奇妙的对数表的说明》一书,这个对数表的出版震动了整个数学界.“对数”一词是纳皮尔首先创造的,意思是“比数”.他最早用“人造的数”来表示对数.俄国著名诗人莱蒙托夫是一位数学爱好者，传说有一次他在解答一道数学题时，冥知识框架例题精讲高考要求第5讲 对数运算和对数函数思苦想没法解决，睡觉时做了一个梦，梦中一位老人揭示他解答的方法，醒后他真的把此题解出来了，莱蒙托夫把梦中老人的像画了出来，大家一看竟是数学家纳皮尔，这个传说告诉我们：纳皮尔在人们心目中的地位是多么的高.(一)知识内容<教师备案>在指数函数x y a =中，对于每个y +∈R ，存在唯一的x 与之对应，幂指数x 叫做以a 为底的y 的对数，这样从y 到x 的对应是指数运算的一个相反运算，让同学思考由函数的定义，判断这是否可以定义一种新的函数？这种运算和对应的函数有什么样的性质呢？1.对数：一般地，如果x a y =(0a >，且1)a ≠，那么数x 叫做以a 为底y 的对数，记作log a x y =，其中a 叫做对数的底数，y 叫做真数.关系式axy指数式 x a y =底数(0,1)a a >≠ 指数(R)x ∈ 幂（值）(R )y +∈对数式 log a y x = 底数(0,1)a a >≠ 对数(R)x ∈ 真数(R )y +∈ 对数恒等式及对数的性质，对数log (0,1)a N a a >≠满足： ⑴零和负数没有对数； ⑵1的对数是零，即log 10a =； ⑶底的对数等于1，即log 1a a =.2.常用对数：通常将以10为底的对数叫做常用对数，并把10log N 记为lg N .3.自然对数：在科学技术中常使用以无理数 2.71828e =为底的对数，以e 为底的对数称为自然对数，并且把log e N 记为ln N .4.对数与指数间的关系：当0,1a a >≠时，log x a a N x N =⇔=.5.指数和对数的互化：log b a a N N b =⇔=.N a N a =log ，log N a a N =（二）主要方法：1.重视对数的概念，应用基础概念解决具体问题2.熟练运用指数和对数的互化板块一：对数的定义和相关概念（三）典例分析：【例1】 ⑴将下列指数式化为对数式，对数式化为指数式：①45625=；②61264-=；③1 5.733m⎛⎫= ⎪⎝⎭；④12log 164=-；⑤lg0.012=-；⑥ln10 2.303=.⑵求下列各式中x 的值：①642log 3x =-；②log 86x =；③lg100x =；④2ln e x -=.【例2】 将下列对数式写成指数式：（1）416log 21-=；（2）2log 128=7；（3）lg0.01=-2；（4）ln10=2.303【例3】 ⑴27log 9，⑵81log 43，⑶()()32log 32-+，⑷625log 345(一)知识内容1.对数的运算性质：如果0a >，且1,0,0a M N ≠>>，那么：⑴log ()log log a a a M N M N ⋅=+；（积的对数等于对数的和） 推广1212log (...)log log ...log a k a a a k N N N N N N ⋅=+++ ⑵log log log aa a MM N N=-；（商的对数等于对数的差） ⑶log log (R)a a M M ααα=∈ ⑷1log log naa N N n=（正数幂的对数，等于幂指数乘以同一底数幂的底数的对数） <教师备案>以性质⑴为例进行证明如下： 已知log a M ，log a N （M 、0N >），求log ()a MN 设log a M p =，log a N q =，根据对数的定义，可得p M a =，q N a = 由p q MN a a =⋅p q a +=∴log ()log log a a a MN p q M N =+=+2.换底公式：log log log a b a NN b=（,0,,1,0a b a b N >≠>） <教师备案>证明： 法一：根据指数的运算性质推导 设log b N x =，则x b N =.两边取以a 为底的对数，得log log a a x b N =， 所以log log a a N x b =，即log log log a b a NN b=. 法二：根据对数恒等式及对数的运算性质推导由对数恒等式得：log log log log ()log bN b a a a N b b N ⋅==，所以有log log log a b a NN b=. 换底公式的意义：把以一个数为底的对数换成以另一个大于0且不等于1的数为底的对数，以达到计算、化简或证明的目的.<教师备案>常见错误：log ()log log a a a M N M N ±=±；log ()log log a a a MN M N =⋅；log log log a aa MM N N=. 3.关于对数的恒等式板块二：对数的运算性质和法则①log a N a N =②log n a a n =③1log log a b b a=④log log n n a a M M = ⑤log log log log a b a b M MN N=（二）主要方法1.解决与对数函数有关的问题，要特别重视定义域；2.解决对数不等式、对数方程时，要重视考虑对数的真数、底数的范围；3.对数不等式的主要解决思想是对数函数的单调性.（三）典例分析【例4】 求下列各值：⑴221log 36log 32-；⑵log ；⑶lg1；⑷3log 53；⑸3log 59；⑹3log 3；⑺；⑻22(lg5)lg 2lg 25(lg 2)+⋅+；⑼827log 9log 32⋅.【例5】 求值：⑴2572lg3lg7lg lg 94++-；⑵32516log 4log 9log 5⋅⋅.【例6】 若a 、0b >，且a 、1b ≠，log log a b b a =，则A.a b =B.1a b=C.a b =或1a b=D.a 、b 为一切非1的正数【例7】 ⑴8log 3p =，3log 5q =，那么lg5等于______（用p ，q 表示）；⑵知18log 9a =，185b =，用,a b 表示36log 45.【点评】⑴换底公式的一个重要应用：log log 1m n n m ⋅=⑵181818log 2log 9=，将未知转化为已知，是对数函数运算性质的重要应用. 【例8】 已知2log 3a =，37b =，求12log 56【例9】 已知lg5m =，lg3n =，用,m n 表示30log 8.【例10】 已知(0,0,1)ab m a b m =>>≠且log m b x =，则log m a 等于A.1x -B.1x +C.1xD.1x -【例11】 已知12()x f x a-=，且(lg )f a =a 的值.【例12】 下列各式中，正确的是A.2lg 2lg x x =B.1log log a a x n =C.log log log a a a x xy y=1log 2a x =【例13】 已知2(3)log (3)1x x x ++=，求实数x 的值.【例14】 设a 为实常数，解关于x 的方程)lg()3lg()1lg(x a x x -=-+-.1.对数函数：我们把函数log (0a y x a =>且1a ≠）叫做对数函数，其中x 是自变量，函数的定义域是(0,)+∞，值域为实数集R .2.对数函数的图象和性质：一般地，对数函数log (0a y x a =>且1a ≠）的图象和性质如下表所示：01a <<1a >图象定义域 (0,)+∞值域 R性质⑴过定点(1,0)，即1x =时，0y =⑵在(0,)+∞上是减函数； （2）在(0,)+∞上是增函数.<教师备案>因为对数函数与指数函数密切相关，所以在学习对数函数的概念、图象与性质时，要处处与指数函数相对照.如：指数函数的值域(0,)+∞，变成了对数函数的定义域；而指数函数的定义域为实数集R ，则变成了对数函数的值域；同底的指数函数与对数函数的图象关于直线y x =对称等.y=log a x (0<a <1)O 1yx y=log a x (a >1)O 1yx板块三：对数函数【例15】 求下列函数的定义域：⑴2log a y x =；⑵log (4)a x -；⑶y .【例16】 求下列函数的定义域：⑴31log (32)y x =-；⑵1log (3)x y x -=-.【例17】 已知()log (1)x a f x a =-(0,a >且1)a ≠，⑴求()f x 的定义域； ⑵讨论函数()f x 的单调性；【例18】 求函数)(log )1(log 11log )(222x p x x x x f -+-+-+=的定义域和值域.【例19】 函数2lg(20)y x x =-的值域是A.y ＞0B.y ∈RC.y ＞0且y ≠1D.y ≤2【例20】 已知函数2()lg[2(1)94]f x mx m x m =++++，⑴若此函数的定义域为R ，求实数m 的取值范围；⑵若此函数的值域为R ，求实数m 的取值范围.【点评】本题涉及到解一元二次不等式的解法，可根据学生情况进行讲解.【例21】 已知函数18log )(223+++=x nx mx x f 的定义域为R ，值域为[0，2]，求m ，n 的值.【例22】 下面结论中，不正确的是A.若a ＞1，则x a y =与x y a log =在定义域内均为增函数B.函数x y 3=与x y 3log =图象关于直线x y =对称C.2log a y x =与2log a y x =表示同一函数D.若01,01a m n <<<<<，则一定有log log 0a a m n >>【例23】 已知),,)(lg()(为常数b a b a x f xx-=①当a ，b ＞0且a ≠b 时，求f (x )的定义域；②当a ＞1＞b ＞0时，判断f (x )在定义域上的单调性，并用定义证明【例24】 在函数10(log <<=a x y a ，)1≥x 的图象上有A ，B ，C 三点，它们的横坐标分别是t ，t ＋2，t ＋4，（1）若△ABC 的面积为S ，求S ＝f （t ）； （2）判断S ＝f （t ）的单调性； （3）求S ＝f （t ）的最大值.【例25】 已知函数22log )(+-=x x x f a的定义域为[],αβ，值域为[]log (1),log (1)a a a a βα--，且)(x f 在[],αβ上为减函数. （1）求证α＞2； （2）求a 的取值范围.【例26】 对于212()log (23)f x x ax =-+，⑴函数的“定义域为R ”和“值域为R ”是否是一回事；⑵结合“实数a 取何值时，()f x 在[1)-+∞，上有意义”与“实数a 取何值时，函数的定义域为(1)(3)-∞+∞，，”说明求“有意义”问题与求“定义域”问题的区别.⑶结合⑴⑵两问，说明实数a 的取何值时()f x 的值域为(1]-∞-，.【例27】 ⑷实数a 取何值时，()f x 在(1]-∞，内是增函数.⑸是否存在实数a ，使得()f x 的单调递增区间是(1]-∞，，若存在，求出a 的值；若不存在，说明理由.【点评】该题主要考察复合对数函数的定义域、值域以及单调性问题.解题过程中遇到了恒成立问题，“恒为正”与“取遍所有大于零的数”不等价，同时又考察了一元二次函数函数值的分布情况，解题过程中结合三个“二次”的重要结论来进行处理.【例28】 比较下列各组数的大小：⑴2log 3.4，2log 8.5；⑵0.3log 1.8，0.3log 2.7；⑶log 5.1a ，log 5.9a (0,a >且1)a ≠;⑷20.3，2log 0.3，0.32.【点评】利用对数函数的性质比较大小的题，一般都可以通过对数函数的单调性，通过直接比较、中间值法或者图象法得到相关结论.如：设110a <<，比较2lg a ，2(lg )a ，lg(lg )a 的大小.1100lg 1a a <<⇒<<，于是22lg(lg )0(lg )lg a a a <<<.【例29】 设2(log )2(0)x f x x =>，则f （3）的值是A.128B.256C.512D.8【例30】 a 、b 、c 是图中三个对数函数的底数，它们的大小关系是A.c ＞a ＞bB.c ＞b ＞aC.a ＞b ＞cD.b ＞a ＞c【例31】 （2005年天津文） 已知111222log log log b a c <<，则（）A.222b a c >>B.222a b c >>C.222c b a >>D.222c a b >>【例32】 如果02log 2log <<b a ，那么a ，b 的关系及范围.【例33】 ⑴若log 2log 20a b <<，则（）A.01a b <<<B.01b a <<<C.1a b >>D.1b a >> ⑵已知2log 13a <，求a 的取值范围.【点评】在上面的对数函数图象中，共有四条对数函数log a y x =，底数a 的大小比较可以通过作一条直线：1y =，于四条曲线分别交于点1234,,,P P P P ，易知，这四点的横坐标即对应相应的底数的值，故比较这四点的横坐标即可.【例34】 已知函数()1log 3x f x =+，()2log 2x g x =，⑴试比较函数值()f x 与()g x 的大小；⑵求方程|()()|()()4f x g x f x g x -++=的解集.【例35】 函数log a y x =在[2,)x ∈+∞上恒有||1y >，求a 的范围.【例36】 已知a ＞0，a ≠1，10<<x ，比较|)1(log |x a +和|)1(log |x a -的大小.【例37】 若23log 1a <，则a 的取值范围是 A.203a <<B.23a >C.213a <<D.203a <<或a ＞1【例38】 若关于23lg lg )lg(=--x a x 至少有一个实数根，则求a 的取值范围.【例39】 设a ，b 为正数，若lg()lg()10ax bx +=有解，则求b a 的取值范围.【例40】 如果2112222log (1)log 2a a a a +++≤，求a 的取值范围.【例41】 已知}2)385(log |{2>+-=x x x A x ，24{|210}B x x x k =-+-≥，要使A B ，求实数k 的取值范围.【例42】 设正数a ，b ，c 满足222c b a =+. （1）求证：1)1(log )1(log 22=-++++bc a a c b ； （2）又设1)1(log 4=++a c b ，32)(log 8=-+c b a ，求a ，b ，c 的值.【例43】 （1）已知0(2log log >=+a y x a a ，)1≠a ，求yx 11+的最小值. （2）已知2052=+y x ，求y x lg lg +的最大值.（3）已知4422=+y x ，求xy 的最大值.【例44】 解方程)12(log 2)22(log 212+=++x x。