SPC统计指标资料

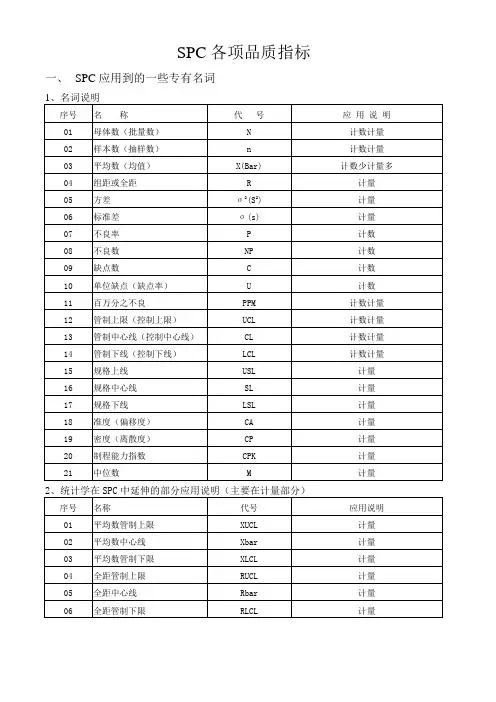
SPC各项品质指标一、SPC应用到的一些专有名词二、品质指标的来源1、产品计量值的规格2、统计学名词（1）组距（R）：一组数据中的最大值减最小值。

R=MAX-MIN（2）平均数（Mean，但通常用Xbar或X表示）：把一组数据全部相加，再除以该组数据的个数。

X=（X1+X2+……Xn）/n（3）中位数（Median,通常用M表示）：把一组数据先按大小顺序排列起来，然后取最中间的一位。

如若该组数据为奇数，则取最中间一位，如若该组数据为偶数，则取中间两位的其中一位。

（4）方差（σ2，有时也用S来表示）：有该组数据中每个数据减实际平均数平方的和再除以该数组数据的个数（N）σ 2 = ∑（Xi-Xbar）2n-1（5）标准差（S）：可直接由方差开平方得来。

S=σ= [（X1-X ）2 +（X2–X）2+…+ （X n-X ）2] /（n-1）3管制界限（1）管制中心线（Center line）即实际数据的平均值（即Xbar）（2）管制上限（Upper Control Level, 缩写为UCL）由Xbar加上三倍的标准差（3）管制下限（Low Control Level, 缩写为LCL）：由Xbar减去三倍的标准差CL=XbarUCL=Xbar+3σLCL= Xbar-3σ4.品质指标工程能力指數(C Pk),是將工程能力的實力與規格相比較,做為判斷工程是否能制出滿足規格的制品.(1).制程准确度Ca(Capability Of Accuracy)Ca =（實際平均值－規格中心值）／規格公差的一半╳100%(X-μ) ×100%T/2規格公差(T)＝規格上限－規格下限＝Su－Si(2). 製程精密度Cp(Capability Of Precision)Cp =規格公差／６倍標準差= T / 6單邊規格時：=規格上限－平均值／３倍標準差或= 平均值－規格下限／３倍標準差(3). 製程能力指數C Pk = (1-K)T / 6δ = (1- Ca) ×Cp(δ表示標準差). 单边规格时CPK=CP工程能力有無之評價基準(4).百万分之不良PPM：有的叫DPPM，它是一个概率的概念。

SPC统计-计数型数据1. 简介SPC〔统计过程控制〕是一种统计方法，用于监测和控制过程的变异性。

计数型数据是SPC中常见的一种类型，它是指对一个过程中发生的事件进行计数或计量的数据。

在生产过程中，计数型数据常用于统计质量缺陷、产品故障等信息。

2. SPC统计-计数型数据的目的SPC统计-计数型数据的目的在于通过对计数型数据进行统计分析，了解和控制过程的变异性，从而实现生产过程的质量控制和改良。

3. SPC统计-计数型数据的方法SPC统计-计数型数据常用的方法有以下几种：3.1 控制图控制图是SPC统计-计数型数据中最常用的图表之一，通过绘制计数型数据的变化趋势以及控制限，可以及时发现过程的异常变异，并进行相应的调整和改良。

常见的控制图包括：•P图：用于统计不良事件的比例的控制图。

P图将观察时间分为假设干子组，然后统计每个子组内不良事件发生的比例，并计算上下控制限，以判断过程是否处于控制状态。

•C图：用于统计不良事件的数量的控制图。

C图将观察时间分为假设干子组，然后统计每个子组内不良事件的数量，并计算上下控制限，以判断过程是否处于控制状态。

•U图：用于统计不良事件的单位数的控制图。

U图将观察时间分为假设干子组，然后统计每个子组内不良事件的单位数〔如每个产品的不良事件数量〕，并计算上下控制限，以判断过程是否处于控制状态。

3.2 过程能力指数过程能力指数用于衡量过程的稳定性和一致性，是SPC统计-计数型数据评估过程能力的重要工具。

常见的过程能力指数有：•Cp指数：Cp指数用于评估过程的一致性，它比拟过程的控制限与规格限的距离。

Cp指数越大，说明过程越稳定，一致性越好。

•Cpk指数：Cpk指数用于评估过程的稳定性和一致性，考虑了过程的中心位置。

Cpk指数越大，说明过程的稳定性和一致性越好。

•Pp指数：Pp指数用于评估过程的一致性，考虑了样本大小的影响。

Pp指数越大，说明过程越稳定，一致性越好。

•Ppk指数：Ppk指数用于评估过程的稳定性和一致性，考虑了过程的中心位置和样本大小的影响。

SPC常用公式和参数SPC（Statistical Process Control，统计过程控制）是一种质量管理方法，通过使用统计方法来监控生产过程中的变异性，以及使过程保持在可控状态，确保产品质量的稳定性。

在SPC中，常用的公式和参数用于描述、分析和控制过程的变异性，以及进行质量指标的计算和分析。

下面是SPC中常用的公式和参数：1. 均值（Mean）：均值是一组数据的平均值，用于描述数据的集中趋势。

均值可以表示为：Mean = (x1 + x2 + ... + xn) / n其中，x1 ~ xn表示一组数据，n表示数据的个数。

2. 范围（Range）：范围用于描述一组数据的离散程度，即最大值与最小值之间的差异。

范围可以表示为：Range = xmax - xmin其中，xmax表示一组数据的最大值，xmin表示最小值。

3. 标准差（Standard Deviation）：标准差是一组数据的离散程度的度量，用于衡量数据的波动性。

标准差可以表示为：Standard Deviation = sqrt[((x1 - mean)^2 + (x2 - mean)^2+ ... + (xn - mean)^2) / n]其中，x1 ~ xn表示一组数据，mean表示数据的均值，n表示数据的个数。

4. 方差（Variance）：方差是标准差的平方，也是一组数据的离散程度的度量。

Variance = (Standard Deviation)^25. 控制图（Control Chart）：控制图是SPC中最常用的工具，它用于监控过程的变异性，并确定过程是否处于可控状态。

在控制图中，常用的参数有：- 中心线（Center Line）：控制图的中心线表示过程的平均值或目标值。

- 控制限（Control Limit）：控制限是确定过程的可控状态的界限。

常用的控制图有三个控制限：- 上控制限（Upper Control Limit，UCL）：表示过程变异性在正常范围内的上限，超过该限制则表明过程存在特殊原因。

SPC数据统计分析与管理什么是SPC数据统计分析与管理？SPC（Statistical Process Control，统计过程控制）是一种用于监控过程稳定性和质量控制的方法。

它利用统计分析手段对过程进行监测和改进，以确保产品或过程处于可接受的控制范围内。

SPC数据统计分析与管理则是指在SPC方法的指导下，对所采集到的数据进行分析和管理，以实现持续改进和控制过程的稳定性。

SPC数据统计分析与管理的重要性SPC方法的应用使得企业能够更有效地管理和控制生产过程，降低产品的变异性，并提高产品质量。

通过对过程进行实时和统计分析，在过程出现异常情况时能够及时采取措施，避免不良品的产生。

同时，SPC还能帮助企业分析和优化生产工艺，减少浪费和成本，提高资源利用率。

SPC数据统计分析与管理的步骤SPC数据统计分析与管理通常包括以下步骤：1.数据采集：收集与要求的指标相关的数据，可以通过传感器、仪器或人工手动输入等方式进行采集。

2.数据处理：对收集到的数据进行处理和整理，包括数据清洗、去除异常值和重复值等。

3.统计分析：使用统计方法对数据进行分析，常见的方法包括数据描述统计、变异分析、均值检验、方差分析等。

4.过程控制：根据统计分析的结果，制定相应的控制策略，对过程进行控制和调整，以保持过程的稳定性。

5.数据监控：定期对采集到的数据进行监控和分析，及时发现过程异常或问题，并采取必要的措施进行调整和改进。

6.持续改进：通过对数据统计分析和过程控制的持续监测和改进，不断提高生产过程的稳定性和产品质量。

SPC数据统计分析与管理的应用场景SPC数据统计分析与管理广泛应用于各个行业和领域，包括制造业、物流业、服务行业等。

以下是一些常见的应用场景：1.制造业：在制造过程中，通过监测关键工艺参数和质量指标的变化，及时发现并纠正生产异常，提高产品质量和生产效率。

2.物流业：对物流中的关键指标进行统计分析和管理，如出货准时率、仓储周期等，以优化物流运作和服务质量。

SPC常用公式和参数SPC（Statistical Process Control，统计过程控制）是一种通过收集和分析数据，对过程进行统计学监控的方法。

它可以帮助企业实时监控生产过程的稳定性和一致性，并通过识别和纠正异常，改善产品质量和生产效率。

SPC常用的公式和参数包括：1. 均值（Mean）：均值是一组数据的平均值，用于描述数据的中心趋势。

计算公式为：均值= Σ数据值 / 数据个数。

2. 范围（Range）：范围是一组数据的最大值与最小值之间的差异，用于描述数据的离散程度。

计算公式为：范围 = 最大值 - 最小值。

3. 方差（Variance）：方差是一组数据与其均值之间的差异的平方和的平均数，用于描述数据的波动程度。

计算公式为：方差= Σ(数据值- 均值)² / 数据个数。

4. 标准差（Standard Deviation）：标准差是方差的算术平方根，用于描述数据的离散程度。

计算公式为：标准差= √方差。

5.Cp指数：Cp指数是过程能力指数，用于评估过程的稳定性，即过程的变异范围是否在产品规格范围内。

计算公式为：Cp=(规格上限-规格下限)/(6*标准差)。

6. Cpk指数：Cpk指数是过程能力指数的修正值，考虑了过程中离规格上下限最远的数据点，用于评估过程的能力。

计算公式为：Cpk =min[(规格上限 - 均值) / (3 * 标准差), (均值 - 规格下限) / (3 * 标准差)]。

7. 控制限（Control Limits）：控制限是一组上限和下限，用于判断过程数据是否正常。

常用的控制限包括平均数控制限（X控制限）和范围控制限（R控制限），计算公式为：X控制限 = 均值± 3 * 标准差，R控制限 = D4 * 范围平均数。

8. 过程能力指数（Process Capability Index）：过程能力指数用于评估过程的能力是否满足产品规格要求，常用的指数包括Cp、Cpk和Cpm。

SPC是Statistical Process Control的简称统计过程控制利用统计的方法来监控过程的状态，确定生产过程在管制的状态下，以降低产品品质的变异SPC：统计过程控制（简称SPC）是一种借助数理统计方法的过程控制工具。

它对生产过程进行分析评价，根据反馈信息及时发现系统性因素出现的征兆，并采取措施消除其影响，使过程维持在仅受随机性因素影响的受控状态，以达到控制质量的目的。

它认为，当过程仅受随机因素影响时，过程处于统计控制状态（简称受控状态）；当过程中存在系统因素的影响时，过程处于统计失控状态（简称失控状态）。

由于过程波动具有统计规律性，当过程受控时，过程特性一般服从稳定的随机分布；而失控时，过程分布将发生改变。

SPC正是利用过程波动的统计规律性对过程进行分析控制。

因而，它强调过程在受控和有能力的状态下运行，从而使产品和服务稳定地满足顾客的要求。

实施SPC的过程一般分为两大步骤：首先用SPC工具对过程进行分析，如绘制分析用控制图等；根据分析结果采取必要措施：可能需要消除过程中的系统性因素，也可能需要管理层的介入来减小过程的随机波动以满足过程能力的需求。

第二步则是用控制图对过程进行监控。

控制图是SPC中最重要的工具。

目前在实际中大量运用的是基于Shewhart原理的传统控制图，但控制图不仅限于此。

近年来又逐步发展了一些先进的控制工具，如对小波动进行监控的EWMA和CUSUM控制图，对小批量多品种生产过程进行控制的比例控制图和目标控制图；对多重质量特性进行控制的控制图。

SPC源于上世纪二十年代，以美国Shewhart博士发明控制图为标志。

自创立以来，即在工业和服务等行业得到推广应用，自上世纪五十年代以来SPC 在日本工业界的大量推广应用对日本产品质量的崛起起到了至关重要的作用；上世纪八十年代以后，世界许多大公司纷纷在自己内部积极推广应用SPC，而且对供应商也提出了相应要求。

在ISO9000及QS9000中也提出了在生产控制中应用SPC方法的要求。

RX -一、 管制图公式说明1. 计量值公式1.1 管制图X 管制图：n 为组内样本量，m 为抽样组数；标准偏差 nσσ=2min max X X R -=估计标准偏差 2^d R=σ 全距平均值 m R m R R R R mi im ∑==+++=121...... 管制上限 → R A X R nd X UCL 22)3(+=+=中心线 → X CL = 管制下限 → R A X R nd X LCL 22)3(-=-=其中 nd A 223=R 管制图： R 的标准偏差 )(23d R d R =σ 管制上限 → R D d Rd R R UCL R 423)(33=+=+=σ中心线 → R CL =管制下限 → R D d Rd R R UCL R 323)(33=-=-=σ 其中 23331d d D -= ， 23431d dD +=mx nx x x x mi in∑=++++==++=1m ....32121 m x x x x x ......X 管制图：第i 组之标准偏差1)(12--=∑=n x xS ni ii∑==mi i S m S 11估计标准偏差 4C S =σ 管制上限 → S A X S n C X UCL 34)3(+=+=中心线 → X CL =管制下限 → S A X S nC X LCL 34)3(-=-=其中nC A 433=S 管制图： 管制上限 → S B UCLs 4= 中心线 → S CLs =管制下限 → S B LCLs 3=1.3 X-Rm 管制图Rm 管制图：移动全距 1--=i i i x x MR nMRMR ni i∑==1管制上限 → MR D UCL 4=中心线 → MR CL =管制下限 → MR D LCL 3=(当n=2时，3D 和4D 以样本数为2来查表)个别管制图管制上限 → 23d MRx UCL += 中心线 → x CL =管制下限 → 23d MRx LCL -= (当n=2时，2d 以样本数为2来查表)**中位数随着计算机技术的发展，计算已经不是困难，逐步被淘汰**2. 计数值公式2.1不良率管制图 ( P Chart )当每组之样本数均相同时：中心线 → ∑==Ki i P K P 11管制上限 → ) 1 , )1(3min(n P P P UCL -+= 管制下限 → ) 0 , )1(3max(nP P P LCL --=当各组之样本数不相同时：中心线 → ∑==Ni i i P n N P 11 ， 其中 k n n n N +++= (21)各组管制上下限分别为 管制上限 → ) 1 , )1(3min(in P P P UCL -+= 管制下限 → ) 0 , )1(3max(in P P P LCL --=2.2不良数管制图 ( Pn Chart )中心线 → n P CL =管制上限 → )1(3P P P UCL n n -+=管制下限 → )1(3P P P LCL n n --= 其中 n P 为各组之不合格数。

SPC统计基础知识简介SPC（Statistical Process Control，统计过程控制）是一种用于监控和管理过程稳定性和可靠性的统计技术。

通过收集样本数据并进行分析，SPC能够及时发现过程中的变异和异常情况，从而帮助组织实现质量改进、成本控制和客户满意度的提高。

本文将介绍SPC的基本概念和常用统计方法，帮助读者理解和运用SPC统计基础知识。

1. SPC的基本概念SPC是一种通过分析过程数据来监控过程稳定性的方法。

它基于以下三个基本统计概念：1.1 均值过程中的均值是指一组样本数据的平均值。

在SPC中，通过计算样本的均值来了解过程的中心位置。

如果样本均值始终在预设的目标值附近波动，说明过程稳定。

1.2 变异过程中的变异是指一组样本数据的离散程度。

在SPC中，通过计算样本数据的变异度来了解过程的稳定性。

如果样本数据的变异度较低且在预设的范围内，说明过程稳定。

1.3 控制界限控制界限是为了判断过程是否处于可接受的控制范围内而设定的。

上下控制界限定义了过程稳定的上下限，超出这一范围的样本数据将被认为是异常值或异常事件。

2. 常用的SPC统计方法2.1 过程能力指数（Cp）过程能力指数是一种衡量过程稳定性和可靠性的指标。

它通过比较过程的变异度和指定的公差范围来评估过程性能。

Cp值越高，说明过程的稳定性和可靠性越好。

2.2 控制图控制图是SPC中最常用的统计工具之一。

它通过绘制样本数据的均值、上下控制界限和中心线来反映过程的变化趋势。

通过控制图，可以及时发现和纠正过程中的变异和异常情况。

2.3 散点图散点图是用来显示两个变量之间关系的图表。

在SPC中，散点图可以用来发现变量之间的相关性和趋势。

通过分析散点图，可以帮助确定工艺参数的合理范围和优化生产过程。

2.4 直方图直方图是用来显示数据分布情况的图表。

在SPC中，直方图可以帮助了解过程数据的分布特征和变异程度。

通过分析直方图，可以判断过程是否正常、是否满足规定要求。