材料力学课后题终极版

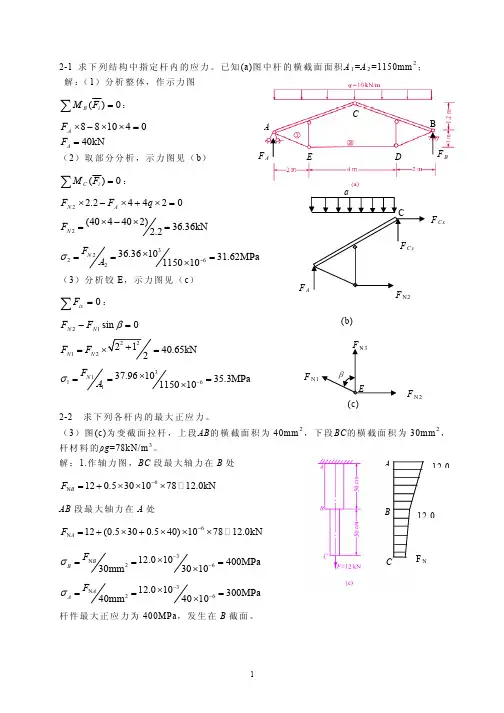
2-1 求下列结构中指定杆内的应力。

已知(a)图中杆的横截面面积A 1=A 2=1150mm 2； 解：（1）分析整体，作示力图∑=0)(i BF M：CB 041088=××−×A F AF N1F N2(c)40kN A F =（2）取部分分析，示力图见（b ）∑=0)(i CF M：02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×（3）分析铰E ，示力图见（c ）∑=0ix F ：0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。

（3）图(c)为变截面拉杆，上段AB 的横截面积为40mm 2，下段BC 的横截面积为30mm 2，杆材料的ρg =78kN/m 3。

解：1.作轴力图，BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ，发生在B 截面。

EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm ，直径缩小了0.022mm ，确定材料的弹性模量E 、泊松比µ。

习题2-2一打入基地内的木桩如图所示，杆轴单位长度的摩擦力fkx2，试做木桩的后力图。

解：由题意可得：l 1 0 fdx F 有kl 3 F k 3F / l 3 3 l FN x1 3Fx 2 / l 3dx F x1 / l 3 0习题2-3 石砌桥墩的墩身高l 10m ，其横截面面尺寸如图所示。

荷载 F 1000kN ，材料的密度2.35kg / m 3 ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：N F G F Alg 2-3 图1000 3 2 3.14 12 10 2.35 9.8 3104.942kN 墩身底面积： A 3 2 3.14 12 9.14m 2 因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

N 3104.942kN 339.71kPa 0.34MPa A 9.14m 2习题2-7 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7 图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：Fdx l F F l dx d l ，l dx EA x 0 EA x E 0 A x r r1 x r r d d1 d ，r 2 1 x r1 2 x 1 ，r2 r1 l l 2l 2 d d1 d d1 d d1 2 d d A x 2 x 1 u2 ，d 2 x 1 du 2 dx 2l 2 2l 2 2l 2l 2l dx d d 2l du dx du ，2 2 1 du 2 d 2 d1 A x u d1 d 2 u l F F l dx 2 Fl l du 因此，l dx 0 u 2 0 EA x E 0 A x E d1 d 2 l 2 Fl 1 l 2 Fl 1 u E d d d d E d1 d 2 0 2 2 d 1 1 x 1 2l 2 0 2 Fl 1 1 E d1 d 2 d 2 d 1 dd1 l 1 2l 2 2 2 Fl 2 2 4 Fl E d1 d 2 d 2 d1 Ed 1 d 2习题2-10 受轴向拉力 F 作用的箱形薄壁杆如图所示。

材料力学课后习题答案1. 弹性力学。

1.1 问题描述，一根钢丝的弹性模量为200GPa，其截面积为0.01m²。

现在对这根钢丝施加一个拉力，使其产生弹性变形。

如果拉力为2000N，求钢丝的弹性变形量。

解答：根据胡克定律，弹性变形量与拉力成正比，与材料的弹性模量和截面积成反比。

弹性变形量可以用以下公式计算：$$。

\delta = \frac{F}{AE}。

$$。

其中，$\delta$表示弹性变形量，F表示拉力，A表示截面积，E表示弹性模量。

代入已知数据，可得：$$。

\delta = \frac{2000N}{0.01m² \times 200GPa} = 0.001m。

$$。

所以，钢丝的弹性变形量为0.001m。

1.2 问题描述，一根长为1m，截面积为$10mm^2$的钢棒，两端受到拉力为1000N的作用。

求钢棒的伸长量。

解答：根据胡克定律，钢棒的伸长量可以用以下公式计算：$$。

\delta = \frac{F \cdot L}{AE}。

$$。

其中，$\delta$表示伸长量，F表示拉力，L表示长度，A表示截面积，E表示弹性模量。

代入已知数据，可得：$$。

\delta = \frac{1000N \times 1m}{10mm² \times 200GPa} = 0.005m。

$$。

所以，钢棒的伸长量为0.005m。

2. 塑性力学。

2.1 问题描述，一块金属材料的屈服强度为300MPa，现在对其施加一个拉力，使其产生塑性变形。

如果拉力为500MPa，求金属材料的塑性变形量。

解答：塑性变形量与拉力成正比，与材料的屈服强度无关。

塑性变形量可以用以下公式计算：$$。

\delta = \frac{F}{A}。

$$。

其中，$\delta$表示塑性变形量，F表示拉力，A表示截面积。

代入已知数据，可得：$$。

\delta = \frac{500MPa}{300MPa} = 1.67。

材料力学性能课后习题答案第一章单向静拉伸力学性能1、解释下列名词。

1弹性比功：金属材料吸收弹性变形功的能力，一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。

2．滞弹性：金属材料在弹性范围内快速加载或卸载后，随时间延长产生附加弹性应变的现象称为滞弹性，也就是应变落后于应力的现象。

3．循环韧性：金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。

4．包申格效应：金属材料经过预先加载产生少量塑性变形，卸载后再同向加载，规定残余伸长应力增加；反向加载，规定残余伸长应力降低的现象。

5．解理刻面：这种大致以晶粒大小为单位的解理面称为解理刻面。

6．塑性：金属材料断裂前发生不可逆永久（塑性）变形的能力。

脆性：指金属材料受力时没有发生塑性变形而直接断裂的能力韧性：指金属材料断裂前吸收塑性变形功和断裂功的能力。

7.解理台阶：当解理裂纹与螺型位错相遇时，便形成一个高度为b的台阶。

8.河流花样：解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。

是解理台阶的一种标志。

9.解理面：是金属材料在一定条件下，当外加正应力达到一定数值后，以极快速率沿一定晶体学平面产生的穿晶断裂，因与大理石断裂类似，故称此种晶体学平面为解理面。

10.穿晶断裂：穿晶断裂的裂纹穿过晶内，可以是韧性断裂，也可以是脆性断裂。

沿晶断裂：裂纹沿晶界扩展，多数是脆性断裂。

11.韧脆转变：具有一定韧性的金属材料当低于某一温度点时，冲击吸收功明显下降，断裂方式由原来的韧性断裂变为脆性断裂，这种现象称为韧脆转变2、说明下列力学性能指标的意义。

答：E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 P15 3、 金属的弹性模量主要取决于什么因素？为什么说它是一个对组织不敏感的力学性能指标？答：主要决定于原子本性和晶格类型。

合金化、热处理、冷塑性变形等能够改变金属材料的组织形态和晶粒大小，但是不改变金属原子的本性和晶格类型。

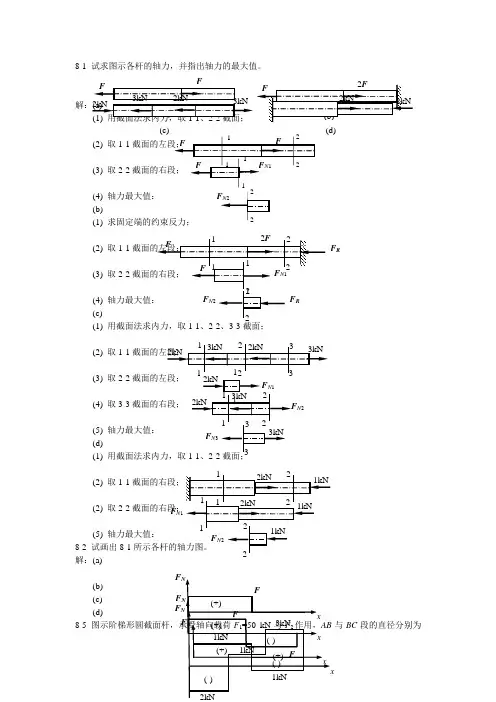
8-1 试求图示各杆的轴力，并指出轴力的最大值。

(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。

解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。

解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。

解：(1) 对节点A(2) 列平衡方程 解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。

解：(1) 对节点A (2) 84 mm 。

8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。

8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形 解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。

习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D 。

1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

习题2-1图习题2-2图习题2-3图习题2-4图1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

第2章 杆件的内力分析2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A ）d d Q x F d M（B ）d d Q x F （C ）d d Q x F （D ）d d Q xF 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。