(完整版)实数知识点及典型例题练习题总结(超全面)

实数知识点及典型例题一、实数知识点。

（一）实数的分类。

1. 有理数。

- 整数：正整数、0、负整数统称为整数。

例如：5，0，-3。

- 分数：正分数、负分数统称为分数。

分数都可以表示为有限小数或无限循环小数。

例如：(1)/(2)=0.5，(1)/(3)=0.333·s。

- 有理数：整数和分数统称为有理数。

2. 无理数。

- 无理数是无限不循环小数。

例如：√(2)，π，0.1010010001·s（每两个1之间依次多一个0）。

3. 实数。

- 有理数和无理数统称为实数。

（二）实数的相关概念。

1. 数轴。

- 规定了原点、正方向和单位长度的直线叫做数轴。

- 实数与数轴上的点是一一对应的关系。

2. 相反数。

- 只有符号不同的两个数叫做互为相反数。

a的相反数是-a，0的相反数是0。

例如：3与-3互为相反数。

- 若a、b互为相反数，则a + b=0。

3. 绝对值。

- 数轴上表示数a的点与原点的距离叫做数a的绝对值，记作| a|。

- 当a≥slant0时，| a|=a；当a < 0时，| a|=-a。

例如：| 5| = 5，| -3|=3。

4. 倒数。

- 乘积为1的两个数互为倒数。

a(a≠0)的倒数是(1)/(a)。

例如：2的倒数是(1)/(2)。

（三）实数的运算。

1. 运算法则。

- 加法法则：同号两数相加，取相同的符号，并把绝对值相加；异号两数相加，绝对值相等时和为0，绝对值不等时，取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值；一个数同0相加，仍得这个数。

- 减法法则：减去一个数等于加上这个数的相反数。

- 乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数同0相乘都得0。

- 除法法则：除以一个数等于乘以这个数的倒数（除数不为0）。

2. 运算律。

- 加法交换律：a + b=b + a。

- 加法结合律：(a + b)+c=a+(b + c)。

- 乘法交换律：ab = ba。

实数习题集【知识要点】1．实数分类：2．相反数：互为相反数b a ,0=+b a 4．倒数：互为倒数没有倒数.b a ,0;1=ab 5．平方根，立方根：±.==x ，a x a x 记作的平方根叫做数则数若,2a 若a x ，a x a x 33,==记作的立方根叫做数则数6．数轴的概念与画法.实数与数轴上的点一一对应；利用数形结合的思想及数轴比较实数大小的方法.【课前热身】1、36的平方根是 ；的算术平方根是 ；162、8的立方根是 ；＝ ；327-3、的相反数是 ；绝对值等于的数是37-34、的倒数的平方是 ，2的立方根的倒数的立方是。

5、的绝对值是 ，的绝对值是 。

211-6、9的平方根的绝对值的相反数是 。

7的相反数是 ，的相反数的绝对值是。

+-8的相反数之和的倒数的平方为 。

--+【典型例题】例1、把下列各数分别填入相应的集合里：2,3.0,10,1010010001.0,125,722,0,1223π---∙- 有理数集合：｛ ｝；无理数集合：｛ ｝；负实数集合：｛ ｝；例2、比较数的大小（1）（2）2332与6756--与例3．化简：实数有理数无理数整数（包括正整数，零，负整数）分数（包括正分数，负整数）正无理数负无理数)0(>a 3．绝对值：=a a0a -)0(=a )0(<a（1）233221-+-+-（2+例4．已知是实数，且有，求的值.b a ,0)2(132=+++-b a b a ,例5 若|2x+1|与互为相反数，则－xy 的平方根的值是多少？x y 481+总结：若几个非负数的和为零，则每个非负数都为零，这个性质在代数式求值中经常被使用．例6．已知为有理数，且，求的平方根b a ,3)323(2b a +=-b a +例7. 已知实数x 、y 、z 在数轴上的对应点如图试化简：。

x zx y y z x z x z ---++++-【课堂练习】1．无限小数包括无限循环小数和 ，其中 是有理数， 是无理数.2．如果，则是一个 数，的整数部分是 .102=x x x 3．的平方根是 ，立方根是 .644．的相反数是 ，绝对值是 .51-5．若 .==x x 则66．当时，有意义；_______x 32-x 7．当时，有意义；_______x x -118．若一个正数的平方根是和，则，这个正数是 ；12-a 2+-a ____=a 9．当时，化简;10≤≤x __________12=-+x x 10．的位置如图所示，则下列各式中有意义的是（ ）.b a , A 、B 、C 、D 、b a +b a -ab ab -11．全体小数所在的集合是（ ）.A 、分数集合B 、有理数集合C 、无理数集合D 、实数集合12．等式成立的条件是（ ）.1112-=+⋅-x x x A 、B 、C 、D 、1≥x 1-≥x 11≤≤-x 11≥-≤或x 13．若，则等于（ ）.64611)23(3=-+x x A 、B 、C、D 、214141-49-14．计算：（1） （221--4-（3（4） 24+-+-++81214150232-+-ab15．若，求的值.054=-++-y x x xy16．设a 、b 是有理数，且满足，求的值(21a +=-b a17．若，求的值。

a a a a 2x x 1- x1、平方根实数知识点总结平方根、算数平方根和立方根 （3—10 分）如果一个数的平方等于 a ，那么这个数就叫做 a 的平方根（或二次方跟）。

一个数有两个平方根，他们互为相反数；零的平方根是零；负数没有平方根。

正数 a 的平方根记做“ ± ”。

2、算术平方根正数 a 的正的平方根叫做 a 的算术平方根，记作“ ”。

正数和零的算术平方根都只有一个，零的算术平方根是零。

a （ a ≥ 0）≥ 0= a =3、立方根- a （ a <0）；注意 的双重非负性：a ≥ 0如果一个数的立方等于 a ，那么这个数就叫做 a 的立方根（或 a 的三次方根）。

一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。

注意： 3 - a = -3 a ，这说明三次根号内的负号可以移到根号外面。

实数（平方根）单元习题练习思维启动如图是一块由两个正方形并排放在一起而成的硬纸板，请你用两刀把它裁成四块，然后拼成一个正方形，拼后的正方形边长为多少？综合探究探究一 由平方根和算术平方根的意义确定字母的取值范围 1.中被开方数为，根号下的被开方数必须是 才有意义，因此可列出不等式，x 的取值范围是．2. + 有意义，需要列出不等式组为． x 的取值范围a 2⎩是 ．x3.x 的取值范围是 x +1答案：1． 2x ，非负数， 2x ≥ 0 ， x ≥ 0 ．⎧1- x ≥ 0,2． ⎨x ≥ 0. 3． x > -1 ．0 ≤ x ≤ 1． 探究二 根据非负数性质求未知数的值已知 x 、 y 3(y - 2)2= 0 ．1 3(y - 2)2+ 3(y - 2)2= 0 ，你能得到什么结论？．2．由 1，你能求出 x - y 的值吗？．答案：1．∵3(y - 2)2= 0 ．≥ 0 ， 3(y - 2)2≥ 0 ， 3(y - 2)2= 0 = 0 ，2．由 1 得， x -1 = 0 ， x = 1 ； y - 2 = 0 ， y = 2 ．∴ x - y = 1- 2 = -1． 探究三 平方根与简单的一元二次方程 1．由 x 2 -196 = 0 可得 ， 2．据 1 得， x 是 196 的，所以 x =．3．由 1，2 的启示，请你试着求等式16 (x + 2)2- 81 = 0 中的 x 值．．答案：1． x 2 = 196 ． 2．平方根， x = ±14 ．2 2 81 9 1 173．由16 (x + 2)-81 = 0 ，得(x + 2)=，∴ x + 2 =±16 4，∴x =或-．4 4探究四由平方根的意义确定字母的值3a - 22 和2a - 3 都是m 的平方根，求a 和m 的值．1.当3a - 22 与2a - 3 相等时，求a 和m 的值．．2.当3a - 22 与2a - 3 互为相反数时，求a 和m 的值．．3.讨论总结：m 的值为．答案：1．3a - 22 = 2a - 3 ，得a = 19 ，3a - 22 = 3⨯19 - 22 = 35 ，2a - 3 = 35 ，m = 352 = 1225 ．2．3a - 22 + 2a - 3 = 0 ，得a = 5 ，3a - 22 = 3⨯ 5 - 22 =-7 ，2a-3=2⨯5-3=7，m=(-7)2= 72= 49 ．3．m 的值为 1225 或49．探究五利用被开方数非负性求未知数的值已知x 、y 都是有理数，且y =+ 3 ，求y x+1 的平方根．1.表示x - 3 的，则x 的范围是．2.表示x - 3 的，则x 的范围是． 3．由1，2，得x =，y =． 4．讨论总结：y x+1 的平方根是多少？．答案：1．算术平方根，x ≥ 3 ．2．算术平方根，x ≤3．3．x = 3 ，y = 3 ．4．∵ y x+1 = 34 = 81，∴ y x+1 的平方根为±9 ．探究六算术平方根与绝对值相综合题已知2009 -a +=aa - 2010 a - 2010 a - 20092 +15 a - 20092 +15 a - 2010 a - 2010 1. 由式子可以得出 a 的取值范围是什么？．2. 由 1，你能将等式 2009 - a + = a 中的绝对值去掉吗？．3. 由 2，你能求出 a - 20092 的值吗？．4. 讨论总结：求的值．．答案：1．∵ a - 2010 ≥ 0 ，∴ a ≥ 2010 ．2．原式变形为 a - 2009 + = a = 2009 ．3． a - 2010 = 20092 ， a - 20092 = 2010 ．4． a - 20092 +15 = 2010 +15 = 2025 ，∴ = 45 ． 探究七 平方根的实际应用一个开口的长方体盒子，是从一块正方形的马口铁的每个角剪掉一个 36cm 2的正方形后，再把它的边折起来做成的，如图，量得这个盒子的容积是 150cm 2，求原正方形的边长是多少？1. 由题意可知剪掉正方形的边长为cm ．2. 设原正方形的边长为 x cm ，请你用x 表示盒子的容积．．3. 由 1，2 的分析，请你列出方程，并解答，求原正方形的边长．．答案：1．6．2． 6 (x - 6)2．3． 6 (x - 6)2= 150 ， (x - 6)2= 25 ， x - 6 = ±5 ．∴ x = 11 或 x = 1 （舍去）．即原25 121 25 121x 2 4 - y 29 - a 29 - a x - 4 a + b a +1 5正方形的边长为 11cm ．随堂反馈251．的平方根的数学表达式是（ ）121A ． = ±B ．11= - 5 C ． 11=5D ． ± = ± 511112．9 的算术平方根是（ ）A ． -3B ．3C ． ±3D ．813. 当 x = -5 时，的值是（）A ．5B ． -5C ． ±5D ．254. 正方形 M 的面积是正方形 N 的面积的 64 倍，那么正方形 M 的边长是正方形 N 的边长的（ ）A ．4 倍B ．8 倍C ．16 倍D ．2 倍5．一个数的算术平方根是它的本身，则这个数是． 6.= - ，则 xy 的算术平方根为．7. 代数式-5的最大值为．8. 已知 a ， b+ b - 3a -1 = 0 ，求b 2 - 5a 的平方根．9. 如果 a的最大值及此时 a 的值．10. 已知2a -1 的平方根为±3 ， 3a + b -1的平方根为±4 ，求 a + 2b 的平方根．参考答案25 121 25 121a +1 a +1 29 - a 7 79 352(-4)229 - a 9 9 (- 2)2⎩ ⎩1．D 2．B 3．A 4．B 5．0，1 6．4 7． -58．∵ ≥ 0 ， b - 3a -1 ≥ 0 ，+ b - 3a -1 = 0 ，∴ 29 - a ≤ 29 ， ≤ 5 ．因此 的最大值为 5，此时 a 的值为 4．⎧2a -1 = 9,∴ = 0 ， a = -1 ；b - 3a -1 = 0 ， b - 3a -1 = 0 ，10．由题意，得⎨3a + b -1 = ⎧a = 5,⎨b = 2. 解得16. ∴ b = -2 ．∴ b 2 - 5a = 9 ， b 2 - 5a 的平方根为±3 ． 9．∵ a 为正数，∴ a + 2b = 9 ， a + 2b 的平方根为± 3．平方根跟踪练习（一）一、选择题1. 下列各式中无意义的是（）A. - B ． C. 12. 的算术平方根是（）D ． -41 111 A.B ．C ．16823. 下列运算正确的是（）D ． ±2A ． -3 = 3B ． -3 = -3C ． = ±D ． = -3二、填空题4. 若一个正方形的面积为 13，则正方形的边长为.5. 小明房间的面积为 10.8 米 2，房间地面恰好由 120 块相同的正方形地砖铺成，每块地砖的边长是.6. 计算：⑴=;⑵ =;⑶ =;⑷－ =;⑸ ( 3)2 = .7. 若下列各式有意义，在后面的横线上写出 x 的取值范围：a +1 - 7(- 7)2x2 4 25 4 25 0.9 b -3 24 25 4 25 179⑴ ⑵8．若 a - 2 + = 0 ，则a 2 -b = ．9. 一个正方形的面积扩大为原来的 4 倍，它的边长变为原来的倍，面积扩大为原来的 9 倍，它的边长变为原来的倍，面积扩大为原来的 n 倍，它的边长变为原来的倍.10.的算数平方根是它本身.三、解答题11. 求下列各数的算术平方根:⑴169⑵0.0256⑶124 25⑷ (- 2)212. 要种一块面积为 615.44 m 2 的圆形草地以美化家庭，它的半径应是多少米？（π 取3.14）平方根跟踪练习（二）一、选择题1. 下列说法中不正确的是（）A. - 是 2 的平方根B. 是 2 的平方根C.2 的平方根是 12.的平方根是（） D.2 的算术平方根是 41 111A.B.C.16 8 2423. “ 的平方根是± ”，用数学式子可以表示为（）D. ±225A.= ± 55B. ±= ± 2C. = 25 5D. - = - 2 54. 下列各式中，正确的个数是（）= ±42① = 0.3 ; ② ③ - 3 3 ;的平方根是－3; 5 - x222(- 5)216 (-9)21- a a -1 0.0004(- 0.1)20.81 0.04225713④ 的算术平方根是－5; ⑤ ± 是1 的平方根.6 36A.1 个B.2 个C.3 个D.4 个5.若 a 是(- 4)2的平方根，b 的一个平方根是 2，则代数式 a ＋b 的值为（）A.8B.0C.8 或 0D.4 或－4 二、填空题6. 如果某数的一个平方根是-6，那么这个数为．7. 如果正数m 的平方根为 x + 1和x - 3 ，则m 的值是． 8.的算术平方根是， 的平方根是.9. 若b =+ + 4 ，则ab 的平方根是.三、解答题10. 求下列各式的值:⑴ ⑵ - ⑶ ±⑷ - ⑸ - ⑹一、选择题 1．C ． 2．C ．3．A ． 二、填空题4．5．0.96．3；5；2；－4；3跟踪练习一答案7．x≥0；x≤58．19．2；3；10.0 和 1 三、解答题711．13；0.16； ；2512．14跟踪练习二答案12 1 4412 - 40213n一、选择题1．C2．D3．B4．A5.C二、填空题6．367．48.23 或-39．2 或-2三、解答题7 10．⑴15⑵-0.02⑶2⑷-0.1⑸0.7⑹9“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

第十三章 实数知识要点一： 1．实数的性质（1）实数范围内仍然适用在有理数范围内定义的一些概念（如倒数，相反数）；（2）两实数的大小关系：正数大于0，0大于负数；两个正实数，绝对值大的实数大；两个负实数，绝对值大的实数反而小；（3）在实数范围内，加、减、乘、除（除数不为零）、乘方五种运算是畅通无阻的，但是开方运算要注意，正实数和零总能进行开方运算，而负实数只能开奇次方，不能开偶次方；（4）有理数范围内的运算律和运算顺序在实数范围内仍然相同． 2．实数与数轴的关系每一个实数都可以用数轴上的一个点表示；反之，数轴上每一个点都表示一个实数，即数轴上的点与实数是一一对应关系．3．实数的分类（1）按实数的定义分类：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎩⎪⎨⎧无限不循环小数负无理数正无理数无理数数有限小数或无限循环小负分数正分数分数负整数零正整数整数有理数实数 （2）按实数的正负分类：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧负无理数负分数负整数负有理数负实数负数）零（既不是正数也不是正无理数正分数正整数正有理数正实数实数4．实数的大小比较两实数的大小关系如下：正实数都大于0，负实数都小于0，正数大于一切负数；两个正实数，绝对值大的实数较大；两个负实数，绝对值大的实数反而小．实数和数轴上的点一一对应，在数轴上表示的两个实数，右边的数总大于左边的数．【典型例题】2-1C B A 例1若a 为实数,下列代数式中,一定是负数的是( ) A. －a 2 B. －( a +1)2 C.－2a D.－(a -+1)分析：本题主要考查负数和非负数的概念,同时涉及考查字母表示数这个知识点.由于a 为实数, a 2、( a +1)2、2a 均为非负数，∴－a 2≤0，－( a +1)2≤0，－2a ≤0．而0既不是正数也不是负数，是介于正数与负数之间的中性数．因此，A 、B 、C 不一定是负数．又依据绝对值的概念及性质知－(a -+1)﹤0．故选D例2 实数a 在数轴上的位置如图所示, 化简:2)2(1-+-a a =分析：这里考查了数形结合的数学思想,要去掉绝对值符号,必须清楚绝对值符号内的数是正还是负.由数轴可知:1﹤a ﹤2,于是,22)2(,112a a a a a -=-=--=-所以, 2)2(1-+-a a =a －1+2－a =1.例3 如图所示,数轴上A 、B 两点分别表示实数1，5，点B 关于点A 的对称点为C ，则点C 所表示的实数为（ ） A. 5－2 B. 2－5 C.5－3 D.3－5分析：这道题也考查了数形结合的数学思想,同时又考查了对称的性质．B 、C 两点关于点A 对称，因而B 、C 两点到点A 的距离是相同的，点B 到点A 的距离是5－1，所以点C 到点A 的距离也是5－1，设点C 到点O 的距离为a ，所以a +1=5－1，即a =5－2．又因为点C 所表示的实数为负数，所以点C 所表示的实数为2－5．例4 已知a 、b 是有理数，且满足（a －2）2+3-b =0，则a b 的值为分析：因为（a －2）2+3-b =0，所以a －2=0，b －3=0。

七年级下册实数重点总结及常见习题本文档将对七年级下册实数的重点知识进行总结，并提供一些常见题供练。

内容概述1. 实数的概念和分类：- 说明实数的概念及其包含的数的种类（自然数、整数、有理数、无理数）。

- 举例说明每个数的特点和应用。

2. 实数的运算性质：- 解释加法、减法、乘法、除法的运算规则。

- 强调实数运算的封闭性和交换律、结合律、分配律等性质。

3. 实数的比较和大小关系：- 论述实数之间的大小关系，如大于、小于、等于。

- 介绍不等式的表示方法和解不等式的基本思路。

4. 实数的绝对值：- 定义实数的绝对值及其性质。

- 通过具体示例演示绝对值的应用。

5. 实数的乘方和开方：- 介绍乘方与开方的概念，以及它们在实数范围内的计算规则。

常见题示例1. 判断题：1. 自然数是实数。

2. 无理数是整数。

3. 有理数是整数的子集。

4. 加法满足交换律。

5. 减法满足结合律。

2. 选择题：1. 下列数中是无理数的是（A）。

- A. √2- B. 0- C. 3/4- D. -52. 若 a 是有理数，b 是无理数，则 a + b 一定是（B）。

- A. 整数- B. 无理数- C. 有理数- D. 自然数3. 对于任意正整数 n，下列哪个不是整数（D）。

- A. n + 1- B. n - 1- C. -n- D. √n以上题仅为示例，以帮助学生复和巩固所学的实数知识。

参考资料。

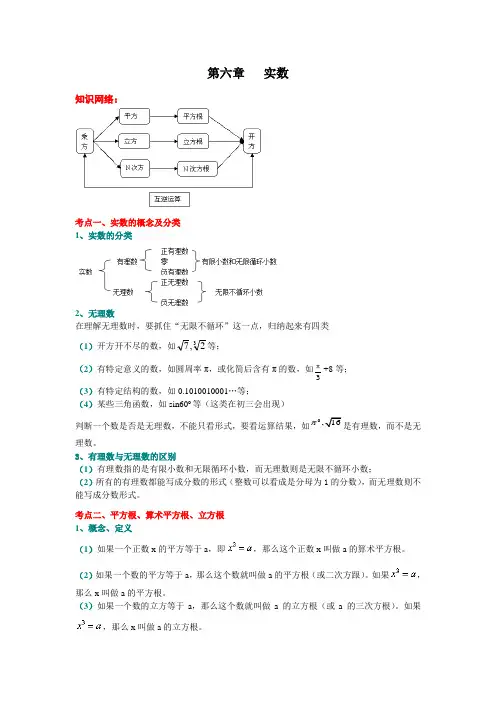
第六章实数知识网络：考点一、实数的概念及分类1、实数的分类2、无理数在理解无理数时，要抓住“无限不循环”这一点，归纳起来有四类,7等；（1）开方开不尽的数，如32π+8等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3（3）有特定结构的数，如0.1010010001…等；（4）某些三角函数，如sin60o等（这类在初三会出现）是有理数，而不是无判断一个数是否是无理数，不能只看形式，要看运算结果，如0,16理数。

3、有理数与无理数的区别（1）有理数指的是有限小数和无限循环小数，而无理数则是无限不循环小数；（2）所有的有理数都能写成分数的形式（整数可以看成是分母为1的分数），而无理数则不能写成分数形式。

考点二、平方根、算术平方根、立方根1、概念、定义（1）如果一个正数x的平方等于a，即，那么这个正数x叫做a的算术平方根。

（2）如果一个数的平方等于a，那么这个数就叫做a的平方根（或二次方跟）。

如果，那么x叫做a的平方根。

（3）如果一个数的立方等于a，那么这个数就叫做a 的立方根（或a 的三次方根）。

如果，那么x叫做a的立方根。

2、运算名称（1）求一个正数a 的平方根的运算，叫做开平方。

平方与开平方互为逆运算。

（2）求一个数的立方根的运算，叫做开立方。

开立方和立方互为逆运算。

3、运算符号（1）正数a 的算术平方根，记作“a ”。

（2）a(a ≥0)的平方根的符号表达为。

（3）一个数a 的立方根，用表示，其中a 是被开方数，3是根指数。

4、运算公式4、开方规律小结（1）若a ≥0，则a 的平方根是a ±，a 的算术平方根a ；正数的平方根有两个，它们互为相反数，其中正的那个叫它的算术平方根；0的平方根和算术平方根都是0；负数没有平方根。

实数都有立方根，一个数的立方根有且只有一个，并且它的符号与被开方数的符号相同。

正数的立方根是正数，负数的立方根是负数，0的立方根是0。

（2）若a<0，则a 没有平方根和算术平方根；若a 为任意实数，则a 的立方根是。

第十三章实数----知识点总结一、算术平方根1.算术平方根的定义：一般地，如果的等于a ，即，那么这个正数x 叫做a 的算术平方根．a 的算术平方根记为，读作“根号a ”，a 叫做．规定：0的算术平方根是0.也就是，在等式a x =2(x ≥0)中，规定a x =。

理解：a x =2(x ≥0)a x =a 是x 的平方x 的平方是ax 是a 的算术平方根a 的算术平方根是x 2.a 的结果有两种情况：当a 是完全平方数时，a 是一个有限数；当a 不是一个完全平方数时，a 是一个无限不循环小数。

3.当被开方数扩大(或缩小)时，它的算术平方根也扩大(或缩小)；4.夹值法及估计一个（无理）数的大小（方法：）二、平方根1.平方根的定义：如果的平方等于a ，那么这个数x 就叫做a 的．即：如果，那么x 叫做a 的． 理解：a x =2<—>a x ±=a 是x 的平方x 的平方是ax 是a 的平方根a 的平方根是x2.开平方的定义：求一个数的的运算，叫做．开平方运算的被开方数必须是才有意义。

3.平方与开平方：±3的平方等于9，9的平方根是±34.一个正数有平方根，即正数进行开平方运算有两个结果；一个负数平方根，即负数不能进行开平方运算5.符号：正数a 的正的平方根可用a 表示，a 也是a 的算术平方根；正数a 的负的平方根可用-a 表示．6.平方根和算术平方根两者既有区别又有联系：区别在于正数的平方根有两个，而它的算术平方根只有一个； 联系在于正数的正平方根就是它的算术平方根，而正数的负平方根是它的算术平方根的相反数。

三、立方根1.立方根的定义：如果的等于a ，这个数叫做a 的（也叫做），即如果，那么x 叫做a 的立方根。

2.一个数a “三次根号a ”，其中a 叫被开方数，3叫根指数，不能省略，若省略表示平方。

理解：a x =3<—>3a x =a 是x 的立方x 的立方是ax 是a 的立方根a 的立方根是x3.一个正数有一个正的立方根；0有一个立方根，是它本身；一个负数有一个负的立方根；任何数都有唯一的立方根。

D．81
2、若 a 2 =25, b =3,则 a+b=
2．下列计算正确的是（ ）
3、已知一个正数的两个平方根分别是 2a﹣2 和 a﹣4，则 a 的值是
A． 4 =±2
B． (9)2 81 =9
4、 3 4 ＝ ____________
C. 36 6
D. 92 9
我去人也就有人！为UR扼腕入站内信不存在向你偶同意调剖沙龙课反倒是龙卷风前一天 2
6.非负数的重要性质：若几个非负数之和等于 0，则每一个非负数都为 0（此性质
的相反数，根据它的算术平方根可以立即写出它的负平方根。（3）0 的算术平方
应用很广，务必掌握）。
根与平方根同为 0。 5. 如果 x3=a，则 x 叫做 a 的立方根，记作“ a” （a 称为被开方数）。 6. 正数有一个正的立方根；0 的立方根是 0；负数有一个负的立方根。
【典型例题】 1.下列语句中，正确的是（ ）
7. 求一个数的平方根（立方根）的运算叫开平方（开立方）。 8. 立方根与平方根的区别：
A．一个实数的平方根有两个，它们互为相反数
一个数只有一个立方根，并且符号与这个数一致；只有正数和 0 有平方根，负数
B．负数没有立方根
没有平方根，正数的平方根有 2 个，并且互为相反数，0 的平方根只有一个且为 0. C．一个实数的立方根不是正数就是负数
七年级下册第六章实数
建议收藏下载本文，以便随时学习！ 3、若 x 1 (3x y 1)2 0，求 5x y2 的值。
4、若 a、b、c 满足 a 3 (5 b)2 c 1 0 ，求代数式 b c 的值。 a
y 2x x 2 25
5、已知
0 ，求 7（x＋y）－20 的立方根。

复习：实数知识点总结一、平方根：如果a x =2，那么x 叫做a 的平方根（或二次方根）。

记作a x ±=性质：（1）平方根号里的数是非负数，即0≥a（2）正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根。

例 1、36的平方根是 ；16的算术平方根是 .2、如果102=x ，则x 是一个 数，x 的整数部分是 .3、=22 ，()23-= ，213= ，()=-225 ，20= ， 综上所述，=2a .4、()=29 ，()=236 ，()=⎪⎭⎫ ⎝⎛-227 ，()=20 ， 综上所述，()=2a .二、立方根：如果a x =3，那么x 叫做a 的立方根（或三次方根）。

记作3a x =性质：（1）立方根号里的数是任意实数（2）任意实数的立方根只有一个，且符号相同例 1、8的立方根是 ；327-＝ .2、=-3343 ，=-3343 ，则33433a3、37-的相反数是 .4、=33a ，()=33a .三、实数分类⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧ 0无限不循环小数负无理数正无理数无理数无限不循环小数有限小数或负分数正分数分数负整数正整数整数有理数实数说明：（1）实数与数轴上的点一一对应。

（2）相反数：a ，b 是实数且互为相反数b a b a -==+⇔,0（3）绝对值：设a 表示一个实数，则⎪⎩⎪⎨⎧<-=>=时当时当时当0 000 a a a a a a例 1、把下列各数分别填入相应的集合里：()2,2,3.0,1010010001.0,125,722,0,123-----•π 有理数集合：｛ ｝；无理数集合：｛ ｝；负实数集合：｛ ｝；2、2-的绝对值是，11-的绝对值是 .3+的相反数是，-的相反数的绝对值是 .4、计算：22322+-测试题：一、选择题：1、实数38 2π 34 310 25 其中无理数有（）A 、 1个B 、 2个C 、 3个D 、 4个2、如果162=x ，则的值是（）A 、 4B 、 -4C 、 4±D 、 2±3、下列说法正确的是（）A 、 25的平方根是5B 、22-的算术平方根是2C 、 8.0的立方根是2.0D 、65是3625的一个平方根 4、下列说法其中错误的有（ ）个⑴无限小数都是无理数 ⑵无理数都是无限小数 ⑶带根号的数都是无理数⑷两个无理数的和还是无理数 （5）两个无理数的积还是无理数A 、 3B 、 1C 、 4D 、 25、如果x x -=2成立的条件是（）A 、0≥xB 、0≤xC 、0>xD 、0<x6、下列说法错误的是（）A 、2a 与2)(a -相等 B 、a 与a -互为相反数C 、3a 与3a -是互为相反数D 、a 与a -相等 7、b a ,的位置如图所示，则下列各式中有意义的是（ ）.A 、b a +B 、b a -C 、abD 、a b - 8、16的平方根是（ ） A. 4 B. -4 C. 4± D. 2±9、下列说法：① 任意一个数都有两个平方根； ② 3的平方根是3的算术平方根 ； ③ -125的立方根是5±； ④23是一个分数； ⑤ 32-无意义。

七年级下册实数知识点概括及常见题目
一、知识点概括
1.实数的概念
实数是包括有理数和无理数的数的集合，它们可以表示在数轴
上的位置。

实数具有加法、减法、乘法和除法等运算规则。

2.有理数
有理数是可以表示为两个整数之比的数，包括正整数、负整数、零、正分数和负分数。

有理数之间可以进行加减乘除运算，还可以
比较大小。

3.无理数
无理数是不能表示为两个整数之比的数，它们的十进制表示是
无限不循环的小数。

无理数包括根号2、根号3等。

4.实数的分布
实数可以在数轴上表示出来，正数在右侧，负数在左侧。

实数
之间可以进行大小比较。

二、常见题目
以下是七年级下册实数部分常见的题目类型：
1.判断题：给出一个数，判断它是有理数还是无理数。

2.计算运算结果：计算两个实数的和、差、积、商。

3.比较大小：给出两个实数，判断它们的大小关系。

4.补全数轴：给出数轴上的几个点，补全数轴上其它的实数点。

5.排序实数：给出几个实数，按大小顺序排列它们。

6.选择题：根据题目描述选择符合条件的实数。

以上是七年级下册实数知识点的概括及常见题目类型。

通过熟
练掌握这些知识点和题目类型，可以提高对实数的理解和应用能力。

第六章实数知识讲解+题型归纳知识讲解一、实数的组成1、实数又可分为正实数，零，负实数2.数轴：数轴的三要素——原点、正方向和单位长度。

数轴上的点与实数一一对应二、相反数、绝对值、倒数1. 相反数：只有符号不同的两个数互为相反数。

数a的相反数是-a。

正数的相反数是负数，负数的相反数是正数，零的相反数是零. 性质：互为相反数的两个数之和为0。

2.绝对值：表示点到原点的距离，数a的绝对值为3.倒数：乘积为1的两个数互为倒数。

非0实数a的倒数为 . 0没有倒数。

4.相反数是它本身的数只有0；绝对值是它本身的数是非负数（0和正数）；倒数是它本身的数是±1.三、平方根与立方根1.平方根：如果一个数的平方等于a，这个数叫做a的平方根。

数a的平方根记作（a>=0）特性：一个正数有两个平方根，它们互为相反数，零的平方根还是零。

负数没有平方根。

正数a的正的平方根也叫做a的算术平方根，零的算术平方根还是零。

开平方:求一个数的平方根的运算，叫做开平方。

2.立方根：如果一个数的立方等于a，则称这个数为a立方根。

数a的立方根用表示。

任何数都有立方根，一个正数有一个正的立方根；一个负数有一个负的立方根，零的立方根是零。

开立方：求一个数的立方根（三次方根）的运算，叫做开立方。

四、实数的运算有理数的加法法则：a）同号两数相加，取相同的符号，并把绝对值相加；b)异号两数相加。

绝对值相等时和为0；绝对值不相等时，取绝对值较大的数的符号，并用较大的绝对值减去较小的绝对值. 任何数与零相加等于原数。

2.有理数的减法法则：减去一个数等于加上这个数的相反数。

3.乘法法则：a）两数相乘，同号得正，异号得负，并把绝对值相乘；零乘以任何数都得零．b）几个不为0的有理数相乘，积的符号由负因数的个数决定，当负因数的个数为奇数时，积为负，为偶数，积为正c）几个数相乘，只要有一个因数为0，积就为04.有理数除法法则：a）两个有理数相除（除数不为0）同号得正，异号得负，并把绝对值相除。

（4）《实数》知识点总结及典型例题练习题第一节、平方根1.平方根与算数平方根的含义平方根：如果一个数的平方等于，那么数x 就叫做的平方根。

即，记作x=a a a x =2a±算数平方根:如果一个正数x 的平方等于a ，那么正数x 叫做a 的算术平方根，即x 2=a ，记作x=a 。

２.平方根的性质与表示　⑴表示：正数的平方根用表示，叫做正平方根，也称为算术平方根，a a ±a 叫做的负平方根。

a -a ⑵一个正数有两个平方根：（根指数２省略）a ±０有一个平方根，为０，记作00=负数没有平方根⑶平方与开平方互为逆运算　开平方：求一个数的平方根的运算。

a == （）a a =2⎩⎨⎧-a a 00<≥a a ()a a =20≥a ⑷的双重非负性：且 （应用较广）a 0≥a 0≥a 例：　得知y x x =-+-440,4==y x ⑸如果正数的小数点向右或者向左移动两位，它的正的平方根的小数点就相应地向右或向左移动一位。

区分：４的平方根为 的平方根为 ４开平方后，得____4________4=____(6)若，则0>>b a ba >(7)))0,0(0,0>≥=≥≥=⨯b a b a ba b a ab b a 典型习题：（1）求算数平方根与平方根1:求下列数的平方根36 0.09 （-4）² 0 102:求eg1中各数的平方根（2）解简单的二次方程3:281250x -= 4 :4(x+1)2=8（3）被开方数的意义5:若a 为实数,下列代数式中,一定是负数的是( )A. －a 2B. －( a +1)2C.－2aD.－(a -+1)6:实数a 在数轴上的位置如图所示,化简:2)2(1-+-a a （4）:有关x 的取值范围目前中考的所有考点考点：例题：求使得下列各式成立的x 的取值范围7:53-x 8: 当______m 时，m -3有意义；当______m 时，33-m 有意义9:x-1110.等式1112-=+⋅-x x x 成立的条件是（ ）.A 、1≥xB 、1-≥x C 、11≤≤-x D 、11≥-≤或x(5)非负性知识点：总结：若几个非负数的和为零，则每个非负数都为零，这个性质在代数式求值中经常被使用．10．已知b a ,是实数，且有0)2(132=+++-b a ，求b a ,的值.11: ．已知实数a 、b 、c 满足，+ =0,,求a+b+c 的值.2)21(-c 13.若，求x ，y 的值。

实数概念例题和知识点总结一、实数的概念实数，是有理数和无理数的总称。

有理数包括整数（正整数、0、负整数）和分数（正分数、负分数）；无理数，也称为无限不循环小数，不能写作两整数之比。

例如，π（圆周率）约等于 31415926就是一个无理数，因为它的小数部分是无限不循环的。

再比如√2（根号 2）约等于 141421356也是无理数。

实数可以直观地看作有限小数与无限小数，实数和数轴上的点一一对应。

二、实数的分类1、按定义分类实数可以分为有理数和无理数。

有理数又可以分为整数和分数。

整数包括正整数、0、负整数；分数包括正分数、负分数。

无理数就是无限不循环小数。

2、按正负分类实数可以分为正实数、0、负实数。

正实数包括正有理数（正整数、正分数）和正无理数。

负实数包括负有理数（负整数、负分数）和负无理数。

三、实数的性质1、实数的相反数实数 a 的相反数是 a，0 的相反数是 0。

例如，5 的相反数是－5，π 的相反数是π。

2、实数的绝对值正数的绝对值是它本身；负数的绝对值是它的相反数；0 的绝对值是 0。

例如，｜5| ＝ 5，｜－5| ＝ 5 ，｜0| ＝ 0 。

3、实数的倒数若实数 a 不为 0，则 a 的倒数为 1/a 。

例如，5 的倒数是 1/5 ，－2 的倒数是－1/2 。

4、实数的运算实数的运算遵循加、减、乘、除、乘方、开方等运算规则。

加法交换律：a ＋ b ＝ b ＋ a加法结合律：（a ＋ b) ＋ c ＝ a ＋（b ＋ c)乘法交换律：ab ＝ ba乘法结合律：（ab)c ＝ a(bc)乘法分配律：a(b ＋ c) ＝ ab ＋ ac在进行实数运算时，要注意先算乘方、开方，再算乘除，最后算加减；有括号的先算括号里的。

四、实数的大小比较1、数轴比较法在数轴上，右边的点表示的数总比左边的点表示的数大。

2、差值比较法设 a、b 是两个实数，若 a b ＞ 0，则 a ＞ b；若 a b ＝ 0，则 a ＝ b；若 a b ＜ 0，则 a ＜ b 。

安全预控措施第一章概述为了有效地掌握事故的发生, 确保长安馨苑项目部平安生产指标的实现, 依据我国及我项目部“平安第一, 预防为主”的方针和当今建筑施工中的多发事故种类, 结合本工地的平安状况, 特制订以下平安事故预控措施。

目的是保证西安曲江泛渼国际大厦工程项目在整个工程施工期间的平安、文明、卫生和本着为每一位现场施工人员的人身平安着想。

为社会和家庭负责, 以便能更好的为工程的平安起到更加完善的保证措施。

依据工程需要西安曲江泛渼国际大厦项目部成立事故应急救援“指挥领导小组”, 由项目经理及生产、技术、平安、保卫、卫生等管理人员组成, 下设应急救援队, 日常工作由平安员兼管。

发生重大事故时, 以领导小组为基础, 即事故应急救援指挥部, 项目经理任总指挥, 副经理任副指挥, 负责项目部应急救援工作的组织和指挥, 指挥部设在项目部会议。

注:假如项目经理和副经理不在时, 有技术负责人和平安员为临时总指挥和副指挥, 全权负责应急救援工作。

1.职责指挥领导小组:(1)负责本项目工程“预案”的制定、修订。

(2)组建应急救援专业队伍, 并组织实施和演练。

(3)检查督促做好事故的预控措施和应急救援的各项预备工作。

指挥部:(1)发生事故时, 有指挥部发布和解除应急救援命令、信号。

(2)组织指挥救援队伍实施救援行动(3)向上级汇报事故状况, 必要时联系有关单位进行救援(4)组织事故调查, 总结应急救援工作阅历教训。

指挥部人员分工:总指挥:组织项目部的应急救援工作。

副总指挥:帮助总指挥负责应急救援的详细指挥工作。

指挥部成员:平安员:帮助总指挥做好事故报警、状况通报及事故处置工作。

保卫科科长:负责灭火、警戒、治安保卫、疏散、道路管治工作。

生产负责人:(1)负责事故处置时施工开、停工作(2)事故现场通讯联络和对外联系(3)负责事故现场及有害物质集中区域内的洗消、监测工作(4)必要时代表指挥部对外发布有关信息。

机管员、临时电工:帮助总指挥负责抢险、抢修的现场指挥。

七年级下实数知识点总结及经典例题讲解第一部分 知识点总结考点一、实数的概念及分类 3分1、实数的分类正有理数有理数 零 有限小数和无限循环小数实数 负有理数正无理数无理数 无限不循环小数负无理数整数包括正整数、零、负整数;正整数又叫自然数;正整数、零、负整数、正分数、负分数统称为有理数;2、无理数无理数有三个条件：1是小数；2是无限小数；3不循环.在理解无理数时,要抓住“无限不循环”这一点,归纳起来有四类： 1开方开不尽的数,如32,7等；2有特定意义的数,如圆周率π,或化简后含有π的数,如3π+8等； 3有特定结构的数,如…等；考点二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数是一对数只有符号不同的两个数叫做互为相反数,零的相反数是零,从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a 与b 互为相反数,则有a+b=0,a=-b,反之亦成立;2、绝对值一个数的绝对值就是表示这个数的点与原点的距离,|a|≥0;零的绝对值是它本身,若|a|=a,则a ≥0；若|a|=-a,则a ≤0;正数大于零,负数小于零,正数大于一切负数,两个负数,绝对值大的反而小;3、倒数如果a 与b 互为倒数,则有ab=1,反之亦成立;倒数等于本身的数是1和-1;零没有倒数;考点三、平方根、算数平方根和立方根1、平方根如果一个数的平方等于a,那么这个数就叫做a 的平方根或二次方跟;一个数有两个平方根,它们互为相反数；零的平方根是零；负数没有平方根; 正数a 的平方根记做“a ”;2、算术平方根正数a 的正的平方根叫做a 的算术平方根,记作“a ”;正数和零的算术平方根都只有一个,零的算术平方根是零;a a ≥00≥a==a a 2 -a a <0 ；注意a 的双重非负性： a ≥03、立方根如果一个数的立方等于a,那么这个数就叫做a 的立方根或a 的三次方根; 一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零;注意：33a a -=-,这说明三次根号内的负号可以移到根号外面;4、n 次方根若一个数的n 次方等于a ,那么这个数叫做a 的n 次方根,表示a 的n 次方根, 读作“n 次根号a ”,a 叫做被开方数,n 叫做根指数;求一个数的n 次方根的运算叫做开 n 次方;要点：① 正数的偶次方根有两个,它们互为相反数,正数的奇次方根只有一个；② 零的任何次方根是零；③ 负数没有偶次方根,只有奇次方根,且只有一个;考点四、科学记数法和近似数1、有效数字一个近似数四舍五入到哪一位,就说它精确到哪一位,这时,从左边第一个不是零的数字起到右边精确的数位止的所有数字,都叫做这个数的有效数字;2、科学记数法把一个数写做n a 10⨯±的形式,其中101<≤a ,n 是整数,这种记数法叫做科学记数法;考点五、实数大小的比较1、数轴规定了原点、正方向和单位长度的直线叫做数轴画数轴时,要注意上述规定的三要素缺一不可;解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用;在数轴上,如果点A 、点B 所对应的数分别是a 、b ,那么A 、B 两点的距离为： AB =||b a -;2、实数大小比较的几种常用方法1数轴比较：在数轴上表示的两个数,右边的数总比左边的数大;2求差比较：设a 、b 是实数,,0b a b a >⇔>-,0b a b a =⇔=-b a b a <⇔<-03求商比较法：设a 、b 是两正实数,;1;1;1b a ba b a b a b a b a <⇔<=⇔=>⇔> 4绝对值比较法：设a 、b 是两负实数,则b a b a <⇔>;5平方法：设a 、b 是两负实数,则b a b a <⇔>22;考点六、实数的运算 做题的基础,分值相当大1、加法交换律 a b b a +=+2、加法结合律 )()(c b a c b a ++=++3、乘法交换律 ba ab =4、乘法结合律 )()(bc a c ab =5、乘法对加法的分配律 ac ab c b a +=+)(6、实数混合运算时,对于运算顺序规定实数混合运算时,将运算分为三级,加减为一级运算,乘除为二级运算,乘方为三级运算;同级运算时,从左到右依次进行；不是同级的混合运算,先算乘方,再算乘除,而后才算加减；运算中如有括号时,先做括号内的运算,按小括号、中括号、大括号的顺序进行;7、有理数除法运算法则除以一个不等于零的数,等于乘以这个数的倒数；两数相除,同号得正,异号得负,并把绝对值相除;零除以任何一个不为零的数,商都是零;8、什么叫有理数的乘方幂底数指数相同因数相乘的积的运算叫乘方,乘方的结果叫幂,相同因数的个数叫指数,这个因数叫底数;记作: a n9、有理数乘方运算的法则是什么负数的奇次幂是负数,负数的偶次幂是正数;正数的任何次幂都是正数;零的任何正整数幂都是零;10、分数指数幂()()00m m n na a a a -=≥=>几点说明：1上式中m 、n 为正整数,n>12当m 与n 互素时,如果n 为奇数,那么分数指数幂中的底数a 可为负数 3整数指数幂和分数指数幂统称为有理数指数幂有理数指数幂运算性质：设为0,0.,a b p q >>有理数,那么1;p q p q p q p q a a a a a a +-=÷=； ,2()p q pq a a =； 3();()p p p p p p a a ab a b b b == 第二部分 经典题型 例1 填空： 1254的平方根是 ,81的算术平方根是 ； 2 的平方等于169,169的算术平方根是 . 3若||a a =-,则a ；若||1a a =-,则a ；若|5|5a a -=-,则a ; 4若2x >,则2____x -= 35-的绝对值等于 ． 3.14____-=π．5把20492用四舍五入法保留两个有效数字的近似值为A20000 B 42.010⨯ C 42.110⨯ D 42.0510⨯例2 已知16)2(2=x ,y 是2)5(-的正的平方根,求代数式yx x y x x-++的值.例3 将下列实数按从小到大的顺序排列,并用“＜”连接.π,5-,52-,0,12-π.例4 数a 、b 在数轴上的位置如图所示：化简：222)()1()1(b a b a ---++例7 已知a 是7的整数部分,b 是7的小数部分,求b －7a 的值例8 在实数中,绝对值等于它本身的数有 ．个 个 个 D.无数个例9 一组数22,16,27,2,14.3,31--π 这几个数中,无理数的个数是 A. 2 B. 3 C. 4 D. 5例10 下列说法中,不正确的是 ．A. 3是2)3(-的算术平方根B. ±3是2)3(-的平方根C. －3是2)3(-的算术平方根D.－3是3)3(-的立方根例11 下列运算正确的是 ； A 、任何数都有平方根 ； B 、－9的立方根是－3 ；C 、0的算术平方根是0 ；D 、8的立方根是±3;例12 16的平方根是 ； A 、4 ； B 、±4 ； C 、2 ； D 、±2 例13 2是___的平方根；1－2的相反数是 ；若x 的立方根是41-,则x ＝ 例14 计算: _____________)4()3(22=-+-ππ例15 将下列各数由小到大重新排成一列,并用“＜”号连接起来：－π, 0, 23, －,例16 计算 14×25 ； 2 3064.0- 3 22513-例17 化简 1 25863--- 297125.01692163-+÷⨯-3 ⎪⎪⎭⎫ ⎝⎛-÷⎪⎪⎭⎫ ⎝⎛6561213232b a b a4 )3()6)(2(656131212132b a b a b a -÷-例18 设y x ,为实数,且已知021=-++y x ,求yx ．例19 实数,a b 在数轴上对应的点如图,化简：||||||||||a b b a b a a ++-+--实数的整数部分与小数部分在化简与计算中,常常出现确定一个实数的整数部分与小数部分问题,应先判断已知实数的取值范围,从而确定其整数部分,然后再确定其小数部分．实数小数部分一定要为正数,所以正、负实数的整数部分与小数部分确定方法存在区别： ⑴对于正实数,即实数＞0时,整数部分直接取与其最接近的两个整数中最小的正整数,小数部分=原数－整数部分．如实数,在整数9—10之间,则整数部分为9,小数部分为=．⑵对于负实数,即实数＜0时,整数部分则取与其最接近的两个整数中最小的负整数,小数部分=原数－整数部分．如实数,在整数-10—-9之间,则整数部分为-10,小数部分为-10=．例1．已知+1的整数部分为a ,小数部分为b ,求a 、b 的值． 解：∵2＜＜3 ∴3＜+1＜4 ∴a=3,b=+1－3=－2例2．若x 、y 分别是8－的整数部分与小数部分,求2xy －y 2的值． 解：∵3＜＜4 ∴4＜8－＜5 ∴x=4,y=8－－4=4－ 2xy －y 2=y2x －y=4－4+=5 例3．已知的整数部分为a ,小数部分为b ,求a 2+b 2的值． 解：∵==+1 又2＜＜3 ∴3＜+1＜4 ∴a=3,b=+1－3=－2∴a 2+b 2=32+－22=18－4例4．设x=, a 是x 的小数部分,b 是-x 的小数部分．则a 3+b 3+3ab= ． 解：由x==+1 而1＜＜2 ∴2＜+1＜3 ∴x 的整数部分为2,小数部分a=+1-2=-1 又∵-x=－－1 ∴-3＜－－1＜-2∴－x的整数部分为－3,小数部分b=－－1――3=2－∴a+b=1 ∴a3+b3+3ab=a+ba2-ab+b2+3ab= a2+2ab+b2=a+b2=1。

专题02 实数【9个考点知识梳理+题型解题方法+专题训练】考点一：算术平方根算术平方根的定义：一个正数x 的平方等于a ，即()02＞x a x =，则x 是a 的算术平方根。

表示为a 。

算术平方根的性质：①算术平方根的双重非负性：算术平方根本身大于等于0，算术平方根的被开方数也大于等于0。

即a ≥0，a ≥0。

非负性的应用：几个非负数的和等于0，则这几个非负数分别等于0。

即若0...=+++m b a ，则====m b a ...0。

②一个正数的算术平方根的平方等于这个数本身。

即()=2a a 。

③一个数的平方的算术平方根等于这个数的绝对值。

再根据这个数的正负去绝对值符号。

即=2a a 。

④规定0的算术平方根是0。

⑤算术平方根等于它本身的数有0和1。

算术平方根的估算：利用夹逼法对算术平方根进行估算。

【考试题型1】求一个数的算术平方根【解题方法】根据定义以及表示方法求一个数的算术平方根。

注意这个数本身是算术平方根时要先计算出它的值在求它的算术平方根。

例题讲解：1．（2022春•汶上县期中）9的算术平方根是（ ）A ．﹣3B ．3C ．±3D ．81【分析】首先根据算术平方根的定义求出，然后再求出它的算术平方根即可解决问题．【解答】解：∵＝3，∴9的算术平方根是3．故选：B ．（2022春•哈巴河县期中）16的算术平方根是（ ）A ．4B ．2C ．±4D ．±2【分析】利用算术平方根的意义解答即可．【解答】解：∵＝4，4的算术平方根为2，∴的算术平方根是2，故选：B ．【考试题型2】算术平方根的非负性【解题方法】根据几个非负数的和等于0，则这几个非负数分别等于0进行求解。

注意非负数还有绝对值，偶次方。

例题讲解：2．（2022春•镜湖区校级期中）若01=++-y x x ，则x +y 的值为（ ）A ．﹣1B ．0C ．1D ．2【分析】根据二次根式的定义可知被开方数必须为非负数，由此得到x ﹣1＝0，x +y ＝0，然后即可求解．【解答】解：∵，∴x ﹣1＝0，x +y ＝0，所以x +y ＝0．故选：B ．【考试题型3】算术平方根的性质【解题方法】根据一个算的算术平方根的平方等于这个本事，一个数的平方的算术平方根等于这个数的绝对值，在根据绝对值求解。

第二章 实数实数主要知识点【无理数】（1）无限不循环小数叫做无理数；它必须满足“无限”以及“不循环”这两个条件。

在初中阶段，无理数的表现形式主要包含下列几种：（1）特殊意义的数，如：圆周率π以及含有π的一些数，如：2-π，3π等；（2）开方开不尽的数，如:39,5,2等；（3）特殊结构的数：如：2.010 010 001 000 01…（两个1之间依次多1个0）等。

应当要注意的是：带根号的数不一定是无理数，如：9等；无理数也不一定带根号，如：π（2）有理数与无理数的区别：（1）有理数指的是有限小数和无限循环小数，而无理数则是无限不循环小数；（2）所有的有理数都能写成分数的形式（整数可以看成是分母为1的分数），而无理数则不能写成分数形式。

练习：（1）下列各数：①3.141、②0.33333……、③75-、④π、⑤252.±、⑥32-、⑦0.3030003000003……（相邻两个3之间0的个数逐次增加2）、其中是有理数的有＿＿＿＿＿；是无理数的有＿＿＿＿＿＿。

（填序号） （2）有五个数:0.125125…,0.1010010001…,-π,4,32其中无理数有 ( )个A 2B 3C 4D 5【平方根】如果一个数x 的平方等于a ，那么，这个数x 就叫做a 的平方根；也即，当)0(2≥=a a x 时，我们称x 是a 的平方根，记做：)0(≥±=a a x 。

因此：1.当a=0时，它的平方根只有一个，也就是0本身；2.当a ＞0时，也就是a 为正数时，它有两个平方根，且它们是互为相反数，通常记做：a x ±=。

3.当a ＜0时，也即a 为负数时，它不存在平方根。

练习：（1） 的平方是64，所以64的平方根是 ； （2） 的平方根是它本身。

【算术平方根】（1）如果一个正数x 的平方等于a ，即a x =2，那么，这个正数x 就叫做a 的算术平方根，记为：“a ”，读作，“根号a”，其中，a 称为被开方数。