存在无风险借贷机会的投资组合的收益率与风险
- 格式:pdf
- 大小:73.35 KB
- 文档页数:2


金融硕士MF金融学综合(风险与收益)历年真题试卷汇编5(题后含答案及解析)题型有:1. 选择题 5. 计算题单项选择题1.(中山大学2013)证券组合风险的大小不仅与单个证券的风险有关,还与各个证券收益间的( )有关。
A.协方差B.标准差C.离差率D.贝塔系数正确答案:A解析:投资组合的方差取决于组合中各种证券的方差和两种证券之间的协方差。
每种证券的方差度量每种证券收益的变动程度;协方差度量两种证券收益之间的相互关系。
在证券方差给定的情况下,如果两种证券收益之间的相互关系或协方差为正,组合的方差就上升;如果两种证券收益之间相互关系或协方差为负,组合的方差就下降。
知识模块:风险与收益2.(清华大学2016)投资者效用函数U=E(r)-Aσ2,在这个效用函数里A 表示( )。
A.投资者的收益要求B.投资者对风险的厌恶C.资产组合的确定等价利率D.对每A单位风险有1单位收益的偏好正确答案:B解析:在各种各样的效用函数中,目前金融理论界使用最广泛的函数是:U=Aσ2,其中A表示投资者的风险厌恶程度,其典型值在2~4之间。
A越高,说明风险厌恶程度越大,说明要求的风险补偿越多。
知识模块:风险与收益3.(对外经贸2014)按照马科维茨的描述,下面的( )资产组合不会落在有效边界上。
A.WB.XC.YD.Z正确答案:D解析:根据马科维茨的描述,落在有效边界上的资产组合当期望收益率相等时,标准差一定是最小的;当标准差相等时,期望收益率一定是最大的。
且期望收益率与标准差是正相关关系,Z组合的期望收益率低于W组合,标准差却大于W组合,所以不会落在有效边界上。
知识模块:风险与收益4.(复旦大学2018)两种资产i和j构成的资产组合中,资产组合的标准差可能降到最低的是( )。
A.ρij=-1B.ρij=0C.ρij=0.3D.ρij=1正确答案:A解析:A、B两种证券组合收益率的方差,用公式表示为:σP2=XA2σA2+XB2σB2+2XAXBρABσAσB如图6—3所示,当ρAB=1时,两种证券A、B的组合P的风险和收益落在直线AB上。

无风险借款对有效集的影响(一)允许无风险借款下的投资组合在推导马科维茨有效集的过程中,我们假定投资者可以购买风险资产的金额仅限于他期初的财富。
然而,在现实生活中,投资者可以借入资金并用于购买风险资产。
由于借款必须支付利息,而利率是已知的。
在该借款本息偿还上不存在不确定性。
因此我们把这种借款称为无风险借款。
为了分析方便起见,我们假定投资者可按相同的利率进行无风险借贷。
1.无风险借款并投资于一种风险资产的情形为了考察无风险借款对有效集的影响,我们首先分析投资者进行无风险借款并投资于一种风险资产的情形。
为此,我们只要对上一节的推导过程进行适当的扩展即可。
我们可以把无风险借款看成负的投资,则投资组合中风险资产和无风险借款的比例也可用X1和X2表示,且X1+X2=1,X1>1,X2<0。
这样,也完全适用于无风险借款的情形。
由于X1>1,X2<0,因此在图上表现为AB线段向右边的延长线上,如图1所示。
这个延长线再次大大扩展了可行集的范围。
图1 无风险借款和风险资产的组合2.无风险借款并投资于风险资产组合的情形同样,由无风险借款和风险资产组合构成的投资组合,其预期收益率和风险的关系与由无风险借款和一种风险资产构成的投资组合相似。
我们仍假设风险资产组合B是由风险证券和C和D组成的,则由风险资产组合B和无风险借款A构成的投资组合的预期收益率和标准差一定落在AB线段向右边的延长线上,如图2所示。
图2 无风险借款和风险组合的组合(二)无风险借款对有效集的影响引入无风险借款后,有效集也将发生重大变化。
在图9中,弧线CD仍代表马科维茨有效集,T点仍表示CD弧线与过A点直线的相切点。
在允许无风险借款的情形下,投资者可以通过无风险借款并投资于最优风险资产组合T使有效集由TD弧线变成AT线段向右边。
图3 允许无风险借款时的有效集这样,在允许无风险借贷的情况下,马科维茨有效集由CTD弧线变成过A、T 点的直线在A点右边的部分。

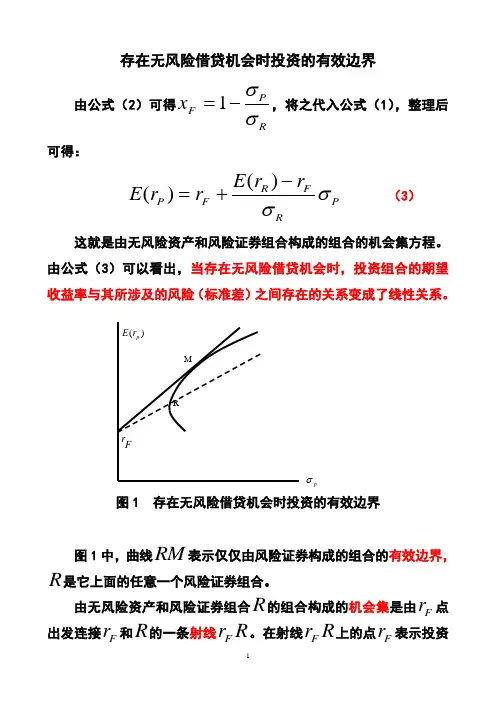
存在无风险借贷机会时投资的有效边界由公式(2)可得RP F x σσ-=1,将之代入公式(1),整理后可得:PRFR F P r r E r r E σσ-+=)()( (3)这就是由无风险资产和风险证券组合构成的组合的机会集方程。
由公式(3)可以看出,当存在无风险借贷机会时,投资组合的期望收益率与其所涉及的风险(标准差)之间存在的关系变成了线性关系。
图1 存在无风险借贷机会时投资的有效边界图1中,曲线RM 表示仅仅由风险证券构成的组合的有效边界,R 是它上面的任意一个风险证券组合。
由无风险资产和风险证券组合R 的组合构成的机会集是由Fr 点出发连接F r 和R 的一条射线R r F。
在射线R r F 上的点Fr 表示投资者将所有资金都投资于无风险资产,所得的收益率为F r ,风险为零;在线段R r F中间的点,表示将一部分资金投资于无风险资产,余下部分投资于风险证券组合R 所构成的组合,是一种“贷出性投资组合”,其收益率大于F r 而小于)(R r E ,风险大于零而小于Rσ,越靠近Fr 的点,无风险证券的投资比重越大,而越靠近R 的点,无风险证券的投资比重越小。
点R 表示将所有资金都投资于风险证券组合R ,所获的期望收益率为)(R r E ,风险为Rσ;射线R r F上R 点右侧延伸线所代表的组合是卖空无风险资产,并将卖空所得与自有资金一起投资于风险证券组合R ,是一种“借入性投资组合”,其期望收益率大于)(R r E ,风险也大于Rσ。
然而,投资于R 点所代表的风险证券组合并非是最佳的,投资者更希望将无风险资产与别的风险证券组合相结合。
射线Mr F由F r 点出发与风险证券有效边界相切,切点M 称为切点投资组合。
除点F r 外,在收益率给定时,射线Mr F是所有由无风险资产和风险证券组合构成的投资机会集中风险最小的;在风险给定时,射线Mr F 是所有由无风险资产和风险证券组合构成的投资机会集中收益率最大的。

金融学综合:证券投资学试题(9)现代证券投资理论一、判断题1、现代证券投资理论是为解决证券投资中收益-风险关系而诞生的。
答案:是2、以马柯维茨为代表的经济学家在20世纪50年代中期创立了名为“资本资产定价模型”的新理论。
答案:非3、证券组合理论由哈里·马柯维茨创立,该理论解释了最优证券组合的定价原则。
答案:非4、证券投资收益的最大化和投资风险的最小化这两个目标往往是矛盾的。
答案:是5、证券组合的预期收益率仅取决于组合中每一证券的预期收益率。
答桠?:非6、收益率的标准差可以测定投资组合的风险。
答案:是7、有效组合在各种风险条件下提供最大的预期收益率。
答案:是8、投资者如何在有效边界中选择一个最优的证券组合,取决于投资者对风险的偏好程度。
答案:是9、投资者所选择的最优组合不一定在有效边界上。
答案:非10、马柯维茨认为,证券投资过程可以分为四个阶段,其中首先应考虑各种可能的证券和证券组合,然后要计算这些证券和证券组合的收益率、标准差和协方差。
答案:是11、CAPM的一个假设是存在一种无风险资产,投资者可以无限的以无风险利率对该资产进行借入和贷出。
答案:是12、无风险资产的收益率为零,收益率的标准差为零,收益率与风险资产收益率的协方差也为零。
答案:非13、引入无风险借贷后,所有投资者的最优组合中,对风险资产的选择是相同的。
答案:是14㠠??在市场的均衡状态下,有些证券在切点组合T中有一个非零的比例,有些证券的组合中的比例为零。
答案:非15、资本市场线上的每一点都表示由市场证券组合和无风险借贷综合计算出的收益率与风险的集合。
答案:是16、资本市场线没有说明非有效组合的收益和风险之间的特定关系。
答案:是17、单项证券的收益率可以分解为无风险利率、系统性收益率和非系统性收益率。
答案:是18、在实际操作中,由于不能确切的知道市场证券组合的构成,我们往往可以用某一市场指数来代替市场证券组合。
答案:是19、一个证券组合的系数等于该组合中各证券系数的总和。




第12章套利定价理论一、单选题下列哪个不是CAPM的假设?()(中央财大2011金融硕士)A.投资者风险厌恶,且其投资行为是使其终期财富的期望效用最大B.投资者是价格承受者,即投资者的投资行为不会影响市场上资产的价格运动C.资产收益率满足多因子模型D.资本市场上存在无风险资产,且投资者可以无风险利率无限借贷【答案】C【解析】套利定价理论(APT)假设资产收益率满足多因子模型。
套利定价模型的优点之一是它能够处理多个因素,而资本资产定价模型就忽略了这一点。
根据套利定价的多因素模型,收益与风险的关系可以表示为:式中,β1代表关于第一个因素的贝塔系数,β2代表关于第二个因素的贝塔系数,依此类推。
二、简答题1.请解释什么是证券组合的系统性风险和非系统性风险,并图示证券组合包含证券的数量与证券组合系统性风险和非系统性风险间的关系。
(对外经贸大学2004研)答:(1)系统风险亦称“不可分散风险”或“市场风险”,与非系统风险相对,指由于某些因素给市场上所有的证券都带来经济损失的可能性,如经济衰退、通货膨胀和需求变化给投资带来的风险。
这种风险影响到所有证券,不可能通过证券组合分散掉。
即使投资者持有的是收益水平及变动情况相当分散的证券组合,也将遭受这种风险。
对于投资者来说,这种风险是无法消除的。
系统风险的大小取决于两个方面,一是每一资产的总风险的大小,二是这一资产的收益变化与资产组合中其他资产收益变化的相关关系(由相关关系描述)。
在总风险一定的前提下,一项资产与市场资产组合收益变化的相关关系越强,系统风险越大,相关关系越弱,系统风险越小。
非系统风险,亦称“可分散风险”或“特别风险”,是指那些通过资产组合就可以消除掉的风险,是公司特有风险,例如某些因素对个别证券造成经济损失的可能性。
这种风险可通过证券持有的多样化来抵消,因此,非系统风险是通过多样化投资可被分散的风险。
多样化投资之所以可以分散风险,是因为在市场经济条件下,投资的收益现值是随着收益风险和收益折现率的变化而变化的。

资本资产定价理论学习心得摘要:资产定价理论源于马柯维茨(Harry Markowtitz)的资产组合理论的研究。
1952年,马柯维茨在《金融杂志》上发表题为《投资组合的选择》的博士论文是现代金融学的第一个突破,他在该文中确定了最小方差资产组合集合的思想和方法,开创了对投资进行整体管理的先河,奠定了投资理论发展的基石,这一理论提出标志着现代投资分析理论的诞生。
在此后的岁月里,经济学家们一直在利用数量化方法不断丰富和完善组合管理的理论和实际投资管理方法,并使之成为投资学的主流理论。
资本资产定价理论主要由证券组合理论、自卑产定价理论和套利定价理论组成。
关键词:资本资产定价模型资产组合收益系统风险套利定价理论一、证券组合投资的收益1952年,哈里M马可维茨发表了一篇具有历史意义的文章。
一般认为这便是现代证券组合理论的雏形。
马可维茨认为,一般的投资者既想要“收益率很大”又想要“收益率非常确定”的想法也许不明智。
投资者在寻求期望收益率最大和不确定性(即风险)最小的过程中,存在两种矛盾的目标,对购买证券做出决策时这两种目标必然相互制约。
组合投资是指某一时点上,一定数额的个人或企业投资中包裹多项资产,例如将一定数额的资金分成几部分,分别投资于国库券、企业债券、优先股和普通股等。
组合投资的收益用组合的期望收益率Rp来用公式表示即为:Rp = Σ Xi Ri = X1 R1 + X2 R2 + … + Xn RnRp = 证券组合的期望收益率;Xi = 投资于证券i的期初价值在证券组合的期初价值中所占比例;n = 证券组合包含的证券种数。
由于证券组合的期望收益率是其组成证券期望收益率的加权平均。
所以,每一证券期望收益率的贡献大小仅仅决定于它的期望收益率大小和它在证券组合的期初市场价值中所占比例。
二、证券组合投资的风险组合投资的风险是指该组合获得的收益率少于其期望收益率的可能性,可用该证券组合收益率的标准差δp来度量。
注会财管知识点:投资组合的风险和报酬投资组合的风险和报酬:1.证券组合的预期报酬率投资组合的预期报酬率等于组合中各单项资产报酬率的加权平均值。
2.(1)协方差协方差为正,表示两项资产的报酬率呈同方向变化;协方差为负,表示两项资产的报酬率呈反方向变化;协方差为绝对数,不便于比较,再者算出某项资产的协方差为某个值,但这个值是什么含义,难以解释。
为克服这些弊端,提出了相关系数这一指标。
(2)相关系数①-1≤r≤1②相关系数=-1,表示一种证券报酬的增长与另一种证券报酬的减少成比例③相关系数=1,表示一种证券报酬率的增长总是与另一种证券报酬率的增长成比例(3)两项资产组合的方差和组合的标准差3.证券组合的机会集和有效集(1)两种证券组合的机会集和有效集相关系数等于1时两种证券组合的机会集是一条直线,此时不具有风险分散化效应;相关系数小于1时,两种证券组合的机会集是一条曲线,表明具有风险分散化效应,相关系数越小,机会集曲线越弯曲,分散化效应越强,相关系数小到一定程度后,机会集曲线会出现向后的凸起,此时存在无效集;相关系数为-1时,机会集曲线变成了一条折线。
机会集曲线最左端的组合称为最小方差组合,从最小方差组合点到最高预期报酬率组合点的那段曲线称为有效集。
(2)多种证券组合的机会集和有效集多种证券组合的机会集不同于两种证券组合的机会集,它不是一条曲线,而是一个平面。
不过其有效集仍然是一条曲线,仍然是从最小方差组合点到最高预期报酬率组合点的那段曲线,也称为有效边界。
4.资本市场线资本市场线指的是一条切线,起点是无风险资产的收益率(Rf),资本市场线与有效边界相切,切点为市场均衡点M.资本市场线的纵轴代表的是“无风险资产与市场组合”的投资组合的期望报酬率,横轴代表的是“无风险资产与市场组合”的投资组合的标准差。
相关的计算公式如下:(1)总期望报酬率=Q×风险组合的期望报酬率+(1-Q)×无风险利率(2)总标准差=Q×风险组合的标准差(3)资本市场线的斜率=(风险组合的期望报酬率-无风险利率)/风险组合的标准差文章摘自:/zhucekuaijishi/。
两个资产收益与风险实际上我们在进⾏投资决策的时候,往往不会只投资⼀种资产,⽽是会同时投资很多资产,当投资很多资产的时候,收益和风险会有⼀些什么样的关系?(⼀)两种资产的收益率⾸先,来看看两种资产,因为当明⽩两种资产之间的关系的时候,很容易就把它扩展到n种资产。
现在假设接下来,⼀期准备投资两种资产,这两种资产的相关系数是p,所有资⾦都⽤来购买这两种资产,所以这两种资产的投资⽐例分别为w1和w2,满⾜W1 +w2=1,组成的新的组合我们称之为P。
问题是:新的组合P,它所具有的期望收益率是多少呢?它所具有的风险⼜是多少呢?先看看收益怎么算?为了计算组合P的收益率,需要知道组合P在期初价值是多少?过了1期以后,在期末价值⼜变成多少?假设这两个资产期初价格分别是P0和Q0,过了1年以后资产价格分别变成了P1和Q1。
现在假设期初投资⾦额为I,分别去购买第1个资产和第2个资产,其中有w1xI投资在第1个资产上,w2xI 投资在第2个资产上。
所以组合P期初价值就是I。
.现在问题是这样⼀个资产组合,在期末的价值是多少呢?这时候需要思考,期初w1xI这么多钱,可以购买多少份第1个资产?其实就是w1xI/P0,所以,第1类资产,期末的价值就变成了w1xI/P0xP1。
类似的,第2类资产期末的价值就变成了w2xI/Q0xQ1。
所以第1期期末资产组合P的价值就变成了,w1xI/P0xP1+w2xI/Q0xQ1,因为W1 +W2=1,⽽P1/P0和Q1/Q0则分别是两个资产的总投资收益。
所以任何⼀个新的组合,其收益率就等于组成这个组合的资产收益率的加权平均,也就是:(⼆)两种资产的风险接下来再看⼀下,这两个资产组成的组合P,它的风险⼜是怎什么样的呢?利⽤概率论的知识,我们知道新的组合,它的⽅差等于组成这个组合的资产的⽅差乘以各⾃的权重的平⽅,再加上两两之间的协⽅差乘以相应的权重。
也就是:两个资产组成的组合的收益率和风险标准差我们都知道了,现在探究下不同的资产组合权重下,这个资产组合的收益和风险之间有什么关系呢?(三)两种资产收益率和风险的关系显然,如果直接观察风险和收益率公式的话,我们很难看出他们之间关系。
一、 无风险资产定义无风险证券的定义单一投资期的情况下,无风险资产的回报率是确定单一投资期的情况下,无风险资产的回报率是确定单一投资期的情况下,无风险资产的回报率是确定。
在单一投资期的情况下,无风险资产的回报率是确定的 无风险资产的标准差为零无风险资产的回报率与风险资产的回报率之间的协方差也是零无风险资产有固定收益,没有任何可能违约的证券二、无风险借贷的含义贷出(risk-free lending ):可以看成是对一种特殊证券,无风险的一种“确定的资产”进行投资。
即对无风险证券的投资被称为“无风险贷出”。
它的预期收益等于无风险利率。
(可理解为“贷出资金”) 借入(risk-free borrowing ):借入可以被认为是一种无风险证券的发行。
即对该无风险资产的持有比例指定一个负值。
(可理解为“借入资金”) 假设假设在无摩擦市场上存在N 种可交易风险证券和一种无风险证券。
以r f 表示无风险利率。
允许无风险贷出后,投资者可以将他的资金的一部分投资于这种无风险资产,并把剩余的部分投资于包含在马科维茨的可行集中的任一投资组合。
令证券f 是无风险的:如果ωf >0,投资者将贷出(投资于无风险资产的比例为正;贷出资金);如果ωf <0,投资者将借入(投资于无风险资产的比例为负;借入资金);如果ωf =0,投资者既不贷出也不借入。
无风险证券的特征:Erf = rf (无风险利率) f oσ= 0fi ρ=fi V =考虑将无风险证券与另一个风险证券组成的组合:1111f f r r r ωωωωσωσ=+=三、带无风险证券的均值-方差证券组合选择问题的解对于有无风险证券情形,我们可以假设除n 种风险证券外,另外还有第0中证券为无风险证券,并且它的无风险利率为f r 。
组合将定义为满足01...1n ωωω+++=的01,,...,n ωωω。
我们仍记12(,,...,)T n w ωωω=,这时,组合的期望收益率为:01122...1f n n r ωμωωμωμωμ=++++=从而1122()()...()()T f f f n n f f r r r r w r ωμωμωμωμμ-=-+-++-=-而组合的方差则显然仍为2T w Vw ωσ=。
存在无风险借贷机会的投资组合的收益率与风险现考虑由n 种证券构成的投资组合P ,组合P 包含无风险资产,其投资比重为F x ;另外)1(-n 种证券都是风险证券,)1(-n 种风险证券在组合P 中总的投资比重为)1(F x -。
我们将仅仅由这)1(-n 种风险证券构成的风险证券组合记为R 。
因此,投资组合P 可以视为由无风险资产和风险证券组合R 的组合而构成。
F x 可以取正数,也可以为负数。
当F x 大于零时,表示投资者将一部分资金投资于风险证券组合R ,将另一部分资金投资于无风险资产,这相当于以无风险利率F r 贷出一部分资金,或者说存在“无风险贷出机会”。
这时,无风险资产与风险证券组合R 的投资比重F x 和)1(F x -都大于零而小于1,我们把这种投资组合称为“贷出性投资组合”。
而当F x 小于零时,表示投资者卖空无风险资产,或者说以无风险利率F r 借入一部分资金,并把所获得的资金与初始自有资金一起投资于风险证券组合R ,即存在着“无风险借入机会”。
这时候,无风险证券的投资比重F x 小于零,而风险证券组合R 的投资比重(1-F x )大于1,我们把这种投资组合称为“借入性投资组合”。
而当F x 等于零时,表示投资者将所有的资金全部投资于风险证券组合R ,即不存在“无风险借贷机会”。
无论是上述三种情况的哪一种情形,无风险资产与风险证券组合R 投资比重之和都等于1。
前面已经讨论了风险证券组合的收益率与风险是如何衡量的,因此在这里,我们假设风险证券组合R 的期望收益率与标准差为已知,分别为R r 与R σ。
由公式(13)可知,存在无风险借贷机会的投资组合P 的期望收益率为:)()1()(R F F F P r E x r x r E -+= (1)因而,存在无风险借贷机会的投资组合的期望收益率为无风险收益率与风险证券组合的期望收益率的加权平均数,其权数为两者在整个投资组合P 中所占的投资比重。
存在无风险借贷机会的投资组合的收益率
与风险
现考虑由种证券构成的投资组合,组合包含无风险资产,其投资比重为;另外种证券都是风险证券,种风险证券在组合中总的投资比重为。
我们将仅仅由这种风险证券构成的风险证券组合记为。
因此,投资组合可以视为由无风险资产和风险证券组合的组合而构成。
可以取正数,也可以为负数。
当大于零时,表示投资者将一部分资金投资于风险证券组合,将另一部分资金投资于无风险资产,这相当于以无风险利率贷出一部分资金,或者说存在“无风险贷出机会”。
这时,无风险资产与风险证券组合的投资比重和都大于零而小于1,我们把这种投资组合称为“贷出性投资组合”。
而当小于零时,表示投资者卖空无风险资产,或者说以无风险利率借入一部分资金,并把所获得的资金与初始自有资金一起投资于风险证券组合,即存在着“无风险借入机会”。
这时候,无风险证券的投资比重小于零,而风险证券组合的投资比重(1-)大于1,我们把这种投资组合称为“借入性投资组合”。
而当等于零时,表示投资者将所有的资金全部投资于风险证券组合,即不存在“无风险借贷机会”。
无论是上述三种情况的哪一种情形,无风险资产与风险证券组合投资比重之和都等于1。
前面已经讨论了风险证券组合的收益率与风险是如何衡量的,因此在这里,我们假设风险证券组合的期望收益率与标准差为已知,分别为与。
由公式(13)可知,存在无风险借贷机会的投资组合的期望收益率为:
(1)
因而,存在无风险借贷机会的投资组合的期望收益率为无风险收益率与风险证券组合的期望收益率的加权平均数,其权数为两者在整个投资组合中所占的投资比重。
由公式(9-14),投资组合收益率的标准差为:
(2)
因此,当存在无风险借贷机会时,投资组合的风险(标准差)等于风险证券组合的投资风险(标准差)与其投资比重的乘积。
例1 设无风险利率为5%,风险证券组合的期望收益率为10%,标准差为8%。
求当无风险资产的投资比重分别为-50%、-10%、0%、10%、50%、100%时整个投资组合的期望收益率与风险。
计算结果由表1所示:
表1 不同无风险资产投资比重下组合P收益率和风险的计算结果
-50%-10%0%10%50%100%
12.5%10.5%10%9.5%7.5%5%
12%8.8%8%7.2%4%0%
从上述计算我们可以看出,随着无风险证券投资比重的增加,投资组合的期望收益率逐渐减小,同时,组合的风险也在减小。