七年级数学上册第四章单元测试题及答案

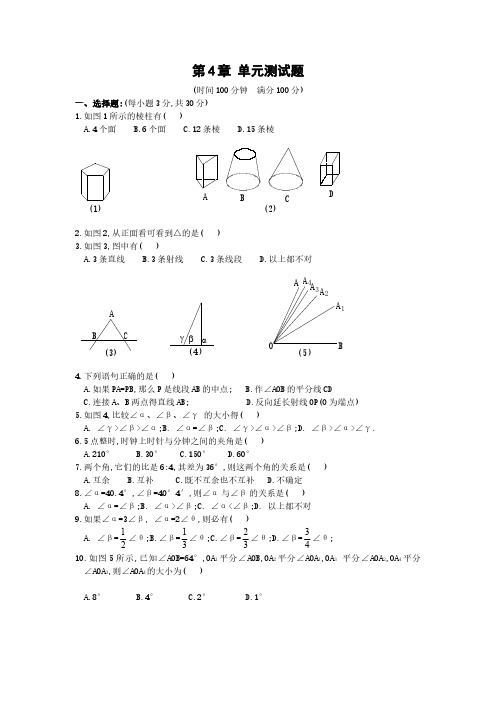
第4章 单元测试题(时间100分钟 满分100分)一、选择题:(每小题3分,共30分)1.如图1所示的棱柱有( )A.4个面B.6个面C.12条棱D.15条棱C(2)A DB2.如图2,从正面看可看到△的是( )3.如图3,图中有( )A.3条直线B.3条射线C.3条线段 D.以上都不对4.下列语句正确的是( )A.如果PA=PB,那么P是线段AB的中点;B.作∠AOB的平分线CDC.连接A、B两点得直线AB;D.反向延长射线OP(O为端点)5.如图4,比较∠α、∠β、∠γ 的大小得( )A. ∠γ>∠β>∠α;B. ∠α=∠β;C. ∠γ>∠α>∠β;D. ∠β>∠α>∠γ.6.5点整时,时钟上时针与分钟之间的夹角是( )A.210°B.30°C.150°D.60°7.两个角,它们的比是6:4,其差为36°,则这两个角的关系是( )A.互余B.互补C.既不互余也不互补D.不确定8.∠α=40.4°,∠β=40°4′,则∠α与∠β的关系是( )A. ∠α=∠β;B. ∠α>∠β;C. ∠α<∠β;D. 以上都不对9.如果∠α=3∠β, ∠α=2∠θ,则必有( )2310.如图5所示,已知∠AOB=64°,OA1平分∠AOB,OA2平分∠AOA1,OA3平分∠AOA2,OA4平分∠AOA3,则∠AOA4的大小为( )A.8°B.4°C.2°D.1°二、填空题:(每小题3分,共30分)11.已知线段AB=8cm,延长AB 至C,使AC=2AB,D 是AB 中点,则线段CD=______.12.如图,从城市A 到城市B 有三种不同的交通工作:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为___________.13.57.32°=_______°_______′_______″;27°14′24″=_____°.14.已知∠a=36°42′15″,那么∠a 的余角等于________.15.∠1+∠2=180°,∠2+∠3=180°,根据________,得∠1=∠3.16.表示O 点南偏东15°方向和北偏东25°方向的两条射线组成的角等于____17.如图,∠AOC=90°,∠AOB=∠COD,则∠BOD=______°.航线铁路公路(6)A B18.102°43′32″+77°16′28″=________;98°12′25″÷5=_____.19.已知线段AB=acm,点A 1平分AB,A 2平分AA 1,A 3平分AA 2,……,____________cm.20.在平面上有任意四点,过其中任意两点画直线,能画_______条直线.三、解答题:(21、24、25、26每题6分,22、23题每题8分)21.根据下列语句画图:(1)画∠AOB=120°;(2)画∠AOB 的角平分线OC;(3)反向延长OC 得射线OD;(4)分别在射线OA、OB、OD 上画线段OE=OF=OG=2cm;(5)连接EF、EG、FG;(6)你能发现EF、EG、FG 有什么关系?∠EFG、∠EGF、∠GEF 有什么关系?22.已知线段AB=10cm,直线AB 上有一点C ,且BC=4cm,M 是线段AC 的中点,求AM 的长.23.如图,直线AB、CD 交于O 点,且∠BOC=80°,OE 平分∠BOC,OF 为OE 的反向延长线.(1)求∠2和∠3的度数.(2)OF平分∠AOD吗?为什么?24.一个角的补角与它的余角的度数之比是3:1,求这个角的度数.25.测量员沿着一块地的周围测绘.从A向东走600米到B,再从B向东南(∠ABC= 135°)走500米到C,再从C向西南(∠BCD=90°)走800米到D.用1厘米代表100米画图, 求DA的长(精确到10米)和DA的方向(精确到1°).北D CA B26.利用线段、角、三角形、圆等图形为你的学校设计一个校标,并简述你的设计思路.参考答案一、选择题1.D2.C3.C4.D5.C6.C7.B8.B9.C 10.B二、填空题11.12cm 12.两点之间,线段最短 13.57、19、12;27.2414. 53°17′45″ 15.同角的补角相等16.140° 17.90 18.180°;19°38′29″.　19. 20.1或4或6三、解答题21.(6)EF=EG=FG,∠EFG=∠EGF=∠FEG=60°22.AM=7cm或3cm23.(1)∠2=100°,∠3=40°;(2)∠AOF=40°,OF平分∠AOD24.设这个角为x0,( 180-x):(90-x)=3:1,x=45.第4章 单元测试题2检测时间：45分钟，满分：100分班级 学号 姓名 得分一、填空题：（每空2分，共46分）1．正方体有______条棱，_____个顶点， 个面.2．圆柱的侧面展开图是一个 ，圆锥的侧面展开图是一个 ，棱柱的侧面展开图是一个 。

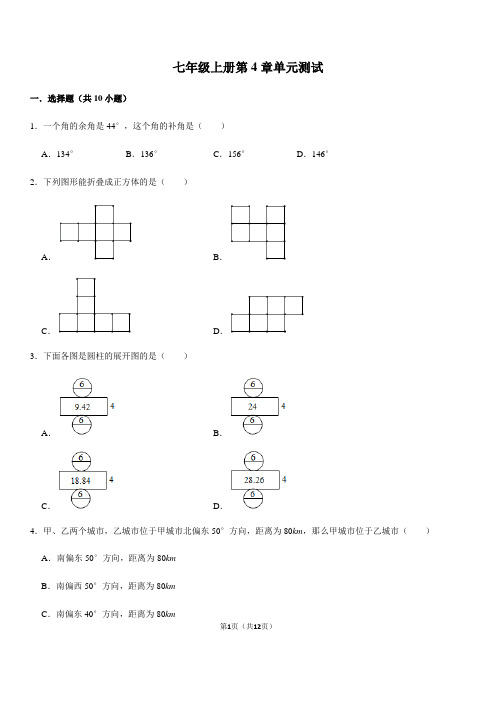
七年级上册第4章单元测试一．选择题（共10小题）1．一个角的余角是44°，这个角的补角是（）A．134°B．136°C．156°D．146°2．下列图形能折叠成正方体的是（）A ．B ．C ．D ．3．下面各图是圆柱的展开图的是（）A ．B ．C ．D ．4．甲、乙两个城市，乙城市位于甲城市北偏东50°方向，距离为80km，那么甲城市位于乙城市（）A．南偏东50°方向，距离为80kmB．南偏西50°方向，距离为80kmC．南偏东40°方向，距离为80km第1页（共12页）D．南偏西40°方向，距离为80km5．有一个正六面体骰子放在桌面上，将骰子如图所示顺时针方向滚动，每滚动90°算一次，则滚动第2020次后，骰子朝下一面的数字是（）A．5B．4C．3D．26．下列各角中，（）是钝角．A ．周角B ．平角C．平角D ．平角7．小明家在学校的南偏西50°方向上，则学校在小明家（）上．A．南偏西50°B．西偏南50°C．北偏东50°D．北偏东40°8．下列度分秒运算中，正确的是（）A．48°39′+67°31′＝115°10′B．90°﹣70°39′＝20°21′C．21°17′×5＝185°5′D．180°÷7＝25°43′（精确到分）9．一个圆柱体切拼成一个近似长方体后（）A．表面积不变，体积变大B．表面积变大，体积不变C．表面积变小，体积不变D．表面积不变，体积不变10．下列语句中，正确的个数是（）第2页（共12页）①直线AB和直线BA是两条直线；②射线AB和射线BA是两条射线；③若∠1+∠2+∠3＝90°，则∠1、∠2、∠3互余；④一个角的余角比这个角的补角小；⑤一条射线就是一个周角；⑥两点之间，线段最短．A．1个B．2个C．3个D．4个二．填空题（共5小题）11．已知，∠A＝46°28'，则∠A 的余角＝．12．一个长方体的高是10cm，它的底面是边长为4cm的正方形，如果底面正方形的边长增加acm，则它的体积增加了cm3．13．已知如图，C是线段AB上的一点，N是线段BC的中点，若AB＝10，AC＝6，则AN＝．14．已知线段AB＝8cm．在直线AB上画线段AC＝5cm，则BC的长是cm．15．如图，将长方形ABCD纸片按如图所示的方式折叠，EF，EG为折痕，点A落在A'，点B落在B'，点A'，B'，E在同一直线上，则∠FEG＝度．三．解答题（共5小题）16．如图，CD是Rt△ABC斜边上的高，请找出图中各对互余的角．第3页（共12页）17．如图，是小明家和学校所在地的简单地图，已知OA＝2km，OB＝3.5km，OP＝4km，点C为OP的中点，回答下列问题：（1）图中到小明家距离相同的是哪些地方？（2）由图可知，公园在小明家东偏南30°方向2km处．请用方向与距离描述学校、商场、停车场相对于小明家的位置．18．如图，已知线段AB＝12 cm，点C为线段AB上的一动点，点D，E分别是AC和BC中点．（1）若点C恰好是AB的中点，则DE ＝cm；（2）若AC＝4 cm，求DE的长；（3）试说明无论AC取何值（不超过12 cm），DE的长不变．第4页（共12页）19．如图，已知射线OB平分∠AOC，∠AOC的余角比∠BOC小42°．（1）求∠AOB的度数：（2）过点O作射线OD，使得∠AOC＝4∠AOD，请你求出∠COD的度数．（3）在（2）的条件下，画∠AOD的角平分线OE，则∠BOE＝．20．如图，平面上有四个点A，B，C，D．（1）根据下列语句画图：Ⅰ、画射线DC；Ⅱ、画直线AC与线段BD相交于点F ；（2）图中以F为顶点的角中，请写出∠AFB的补角．第5页（共12页）参考答案一．选择题（共10小题）1．解：∵一个角的余角是44°，∴这个角的度数是：90°﹣44°＝46°，∴这个角的补角是：180°﹣46°＝134°．故选：A．2．解：A、能折叠成正方体，故此选项符合题意；B、出现了“凹”字格，不能折叠成正方体，故此选项不符合题意；C、折叠后有两个面重合，不能折叠成正方体，故此选项不符合题意；D、出现了“田”字格，不能折成正方体，故此选项不符合题意．故选：A．3．解：由图可知，该圆柱底面直径为6，高为4，所以该圆柱的底面周长（圆柱侧面展开得到的长方形的长）为：6×3.14＝18.84，故选：C．4．解：如图：第6页（共12页）∵乙城市位于甲城市北偏东50°方向，距离为80km，∴甲城市位于乙城市南偏西50°方向，距离为80km，故选：B．5．解：观察图形知道点数三和点数四相对，点数二和点数五相对且四次一循环，∵2020÷4＝505，∴滚动第2020次后与第一个相同，∴朝下的数字是3的对面4，故选：B．6．解：平角＝180°，钝角大于90°而小于180°，平角＝×180°＝120°，是钝角．故选：B．7．解：∵小明家在学校的南偏西50°方向上，∴学校在小明家北偏东50°方向上．故选：C．8．解：48°39'+67°31'＝115°70'＝116°10'，故A选项错误；90°﹣70°39'＝19°21'，故B选项错误；21°17'×5＝105°85'＝106°25'，故C选项错误；180°÷7＝25°43'，故D选项正确．故选：D．9．根据立体图形的切拼方法可知：圆柱体切拼成一个长方体后，体积大小不变，表面积增加了两个以圆柱的高和第7页（共12页）底面半径为边长的长方形的面积，所以表面积变大了．故选：B．10．解：①直线AB和直线BA是一条直线，原来的说法是错误的；②射线AB和射线BA是两条射线是正确的；③互余是指的两个角的关系，原来的说法是错误的；④一个角的余角比这个角的补角小是正确的；⑤周角的特点是两条边重合成射线．但不能说成周角是一条射线，原来的说法是错误的；⑥两点之间，线段最短是正确的．故正确的个数是3个．故选：C．二．填空题（共5小题）11．解：∵∠A＝46°28′，∴∠A的余角＝90°﹣46°28′＝43°32′．故答案为：43°32′．12．解：长方体原体积为：4×4×10＝160cm3．底面边长增加acm后，边长为（4+a）cm，体积为：10（4+a）2＝（10a2+80a+160）cm3．体积增加为：10a2+80a+160﹣160＝10a2+80a．故答案为：（10a2+80a）．13．解：∵AB＝10，AC＝6，∴CB＝10﹣6＝4，第8页（共12页）∵N是线段BC的中点，∴CN＝2，∴AN＝AC+CN＝6+2＝8．14．解：当C点在线段AB上时，BC＝AB﹣AC＝8﹣5＝3（cm）；当C点在线段BA的延长线上时，BC＝AB+AC＝8+5＝13（cm）．故BC的长为3或13cm．故答案为3或13．15．解：由折叠可得∠AEF＝∠A'EF，∠BEG＝∠B'EG，∵∠AEB＝180°，∴∠FEG＝∠A'EF+∠B'EG ＝∠AEB＝90°，故答案为90．三．解答题（共5小题）16．解：∵CD⊥AB，∴△ABC，△BCD是直角三角形，又∵△ABC是直角三角形，∴∠A与∠B，∠A与∠ACD，∠B与∠BCD互余（直角三角形的两个锐角互余），又∵∠ACB＝90°，∴∠ACD与∠BCD互余．∴图中互余的角有：∠A与∠B，∠A与∠ACD，∠B与∠BCD，∠ACD与∠BCD．17．解：（1）因为点C为OP的中点，第9页（共12页）所以OC＝2km，因为OA＝2km，所以可得出距小明家距离相同的是学校和公园；（2）由图可知，学校在小明家东偏北45°方向2km处，商场在小明家西偏北60°方向3.5km处，停车场在东偏南30°方向4km处．18．解：（1）∵点D，E分别是AC和BC的中点，∴DC ＝AC，CE ＝CB，∴DC+CE ＝（AC+CB）＝6cm；故答案为：6．（2）∵AC＝4cm，∴CD＝2cm，∵AB＝12cm，AC＝4cm，∴BC＝8cm，∴CE＝4cm，DE＝DC+CE＝6cm；（3）∵点D，E分别是AC和BC的中点，∴DC ＝AC，CE ＝CB，∴DC+CE ＝（AC+CB），即DE ＝AB＝6cm，故无论AC取何值（不超过12 cm），DE的长不变．第10页（共12页）19．解：（1）由射线OB平分∠AOC可得∠AOC＝2∠BOC，设∠BOC＝x，则∠AOC＝2x，依题意列方程90°﹣2x＝x﹣42°，解得：x＝44°，即∠AOB＝44°．（2）由（1）得，∠AOC＝88°，①当射线OD在∠AOC内部时，∠AOD＝22°，则∠COD＝∠AOC﹣∠AOD＝66°；②当射线OD在∠AOC外部时，∠AOD＝22°则∠COD＝∠AOC+∠AOD＝110°；（3）∵OE平分∠AOD，∴∠AOE ＝，当射线OD在∠AOC内部时，∠BOE＝∠AOB﹣∠AOE＝44°﹣11°＝33°；当射线OD在∠AOC外部时，∠BOE＝∠AOB+∠AOE＝44°+11°＝55°．∴∠BOE度数为33°或55°．故答案为：33°或55°20．解：（1）作图如下：第11页（共12页）（2）∠AFB的补角为∠BFC，∠AFD．第12页（共12页）。

2024年人教版七年级上册数学第四单元课后练习题（含答案和概念）试题部分一、选择题：1. 在下列各数中，哪个数是有理数？（）A. √3B. πC. 3.14D. √12. 下列运算中，哪个运算是整式加减？（）A. 2x + 3yB. 2x × 3yC. 2x ÷ 3yD. 2x² + 3y²3. 若a=3，b=2，则a+b的值为（）A. 5B. 5C. 1D. 14. 下列各式中，哪个是单项式？（）A. 3x + 2yB. 3x²yD. 3x²y²5. 计算下列各式的值：（）A. |3| = 3B. |3| = 3C. |3 5| = 2D. |3 + 5| = 26. 下列各数中，哪个是正数？（）A. 3B. 0C. √1D. 27. 下列各式中，哪个是同类项？（）A. 3x和2yB. 3x²和2xC. 3x²和2x²D. 3xy和2x²y8. 若3x=12，则x的值为（）A. 3B. 4C. 5D. 69. 下列各式中，哪个是多项式？（）A. 3x²C. 3x² + 2xyD. 3x²y²10. 计算下列各式的值：（）A. 3² = 9B. (3)² = 9C. √36 = 6D. √25 = 5二、判断题：1. 有理数包括整数和分数。

（）2. 无理数是无限不循环小数。

（）3. 3x和3x²是同类项。

（）4. 单项式是只有一个项的整式。

（）5. 多项式是由多个单项式相加或相减而成的。

（）6. 0是正数。

（）7. |3 5| = |3 + 5|。

（）8. π是一个有理数。

（）9. 3x²y和2x²y是同类项。

（）10. 若a=3，b=2，则ab的值为5。

（）三、计算题：1. 计算：(3/4) (2/3)。

第四章综合测试一、单选题1.下列判断错误的是（）A .若a b =，则33ac bc -=-B .若a b =，则33a b =--C .若ax bx =，则a b=D .若2x =，则22x x=2.已知3x k =-，2y k =+，则y 与x 的关系是（ ）A .5x y +=B .1x y +=C .1x y -=D .1y x =-3.下列各式不是方程的是（ ）A .20x x +=B .0x y +=C .1x x+D .0x =4.将372x x -=变形正确的是（ ）A .327x x +=B .327x x -=-C .327x x +=-D .327x x -=5.下列等式的变形中，不正确的是（ ）A .若x y =，则55x y +=+B .若(0)x ya a a=¹，则x y =C .若33x y -=-，则x y=D .若mx my =，则x y=6.有一应用题：“李老师存了一个两年的定期储蓄5 000元，到期后扣除20%的利息税能取5 176元，求这种储蓄的年利率是多少？”四位同学都是设这种储蓄的年利率是x ，可他们列出的方程却不同，下列列出的方程中正确的是（）A .5000(1220%)5176x +´´=B .5000(12)80%5176x +´=C .50005000280%5176x +´´=D .5000500080%5176x +´=7.下列方程为一元一次方程的是（ ）A .123+=B .423m n m+=C .2223x x+=D .423x x-=8.下列利用等式的性质，错误的是（）A .若a b =，则11a b -=-B .若237a b +=-，则255a b +=-C .若a b =，则22ma mb =D .若ac bc =，则a b=二、填空题9.一件商品按成本价提高20%后标价，又以9折销售，售价为270元.设这件商品的成本价为x 元，则可列方程：________10.若13x --=，则x =________11.一组数：2，1，3，x ，7，9-，…，满足“从第三个数起，前两个数依次为a 、b ，紧随其后的数就是2a b -”，例如这组数中的第三个数“3”是由“221´-”得到的，那么这组数中x 表示的数为________.12.若代数式7y -与21y -的值相等，则y 的值是________.13.已知关于x 的方程231x a -=-的解为1x =-，则a 的值等于________.14.当x =________时，代数式21x +与58x -的值互为相反数.15.当x =________时，式子1x -与式子214x -的值相等.16.写出一个满足下列条件的一元一次方程：①某个未知数的系数是3；②方程的解是2；这样的方程是________.17.已知3x =-是方程(21)40k x +-=的解，则k =________.三、计算题18.解方程：（1）2523163x x x +--=-；（2）2130.20.5x x -+-=.19.解方程：（1）3723x x+=-（2）3(2)(21)x x x -=--（3）12123x x-=+.20.解方程：31112x x -+=+.四、综合题21.已知方程323452x x -=-（1）求方程的解；（2）若上述方程与关于x 的方程383()2a x a a +=+-是同解方程，求a 的值；（3）在（2）的条件下，a 、b 在数轴上对应的点在原点的两侧，且到原点的距离相等，c 是倒数等于本身的数，求2005()a b c ++的值.第四章综合测试答案解析一、1.【答案】C【解析】A .利用等式性质1，两边都减去3，得到33a b -=-，所以A 成立；B .利用等式性质2，两边都除以3-，得到33a b=--，所以B 成立；C .因为x 必须不为0，所以C 不成立；D .利用等式性质2，两边都乘x ，得到22x x =，所以D 成立；故选C .2.【答案】A【解析】3x k =-Q ，2y k =+，325x y k k \+=-++=.故选：A .3.【答案】C【解析】解：A .20x x +=是方程，x 是未知数，式子又是等式，故本选项不符合题意；B .0x y +=是方程，x 、y 是未知数，式子又是等式，故本选项不符合题意；C .1x x+是分式，不是等式，故本选项符合题意；D .0x =是方程，x 是未知数，式子又是等式，故本选项不符合题意；故选：C .4.【答案】D【解析】等式两边都加7得：327x x =+，等式两边都减2x 得：327x x -=.故选D .5.【答案】D【解析】A .若x y =，根据等式的性质1，两边同时加5可得55x y +=+，故正确；B .若(0)x ya a a=¹，根据等式的性质2，两边同时乘以(0)a a ¹可得x y =，故正确；C .若33x y -=-，根据等式的性质2，两边同时除以3-可得x y =，故正确；D .若mx my =，根据等式的性质2，两边同时除以m ，(0)m ¹，才可得x y =，缺少条件，错误.故选D .6.【答案】C【解析】解：设这种储蓄的年利率为x ，由题意得500050002(120%)5176x +´´-=，即50005000280%5176x +´´=.故答案为：C .7.【答案】D【解析】A .不含有未知数，是等式，不是方程，故选项错误；B .是二元一次方程，故选项错误；C .未知数的最高次数是2次，不是一元一次方程，故选项错误；D .符合一元一次方程的定义，故选项正确.故选D .8.【答案】D【解析】当0c =时，0ac bc ==，但a 不一定等于b ，故D 错误.故答案为：D .二、9.【答案】(120%)0.9270x +´=【解析】解：标价为(120%)x ´+，\可列方程为：(120%)0.9270x +´=.10.【答案】4-【解析】解：等式的两边同时加1得，1131x --+=+，即4x -=，等式的两边同时除以1-得，4x =-.故答案为：4-.11.【答案】1-【解析】解：Q 该组数列满足“从第三个数起，前两个数依次为a 、b ，紧随其后的数就是2a b -”，2131x \=´-=-.故答案为：1-.12.【答案】6-【解析】解：Q 代数式7y -与21y -的值相等，7=21y y \--，移项、合并同类项，可得：=6y -.故答案为：6-.13.【答案】13-【解析】解：把1x =-代入方程231x a -=-得：231a --=-，解得：13a =-，故答案为：13-.14.【答案】1【解析】解：根据题意得：21580x x ++-=，移项合并得：77x =，解得：1x =，故答案为：1.15.【答案】32【解析】由式子1x -与式子214x -的值相等，得2114x x --=，去分母得：4421x x -=-解得：32x =.16.【答案】360x -=【解析】解：由题意可知：3a =，2x =.则将a 与x 的值代入0ax b +=中得：320b ´+=，解得：6b =-，所以，该一元一次方程为：360x -=.故答案为：360x -=.17.【答案】76-【解析】解： 3 x =-Q 是方程(21)40k x +-=的解，(2k 1)(3)40\+´--=，解得：76k =-.故答案为：76-.三、18.【答案】（1）解：去分母得：625646x x x --=-+，移项合并得：817x =，解得：178x =.（2）解：方程整理得：510223x x ---=，移项合并得：315x =，解得：5x =.【解析】（1）方程去分母，去括号，移项合并，把未知数系数化为1，即可求出解.（2）方程整理后，去分母，去括号，移项合并，把未知数系数化为1，即可求出解.19.【答案】（1）移项合并得：416x =，解得：4x =.（2）去括号得：3621x x x -=-+，移项合并得：47x =，解得：74x =.（3）去分母得：3(1)46x x -=+，去括号得：3346x x -=+，解得：9x =-.【解析】（1）方程移项合并，把x 系数化为1，即可求出解.（2）方程去括号，移项合并，把x 系数化为1，即可求出解.（3）方程去分母，去括号，移项合并，把x 系数化为1，即可求出解.20.【答案】解：方程两边都乘2得：31222x x -+=+，移项得：32212x x -=+-，合并同类项得：1x =.【解析】按照去分母，移项，合并的计算过程计算即可.四、21.【答案】（1）解：方程两边同时乘以10得：2(32)53410x x -=´-´，去括号得：641540x x -=-，移项得：615440x x -=-，合并同类项得：936x -=-，系数化为1得：4x =.（2）解：4x =Q 是方程383()2a x a a +=+-的解，383(4)2a a a \+=+-，解得：2a =.（3）解：2a =Q ，2b \=-，又c Q 是倒数等于本身的数，1c \=±，当1c =时，20052005()(221)1a b c \++=-+=；当1c =-时，20052005()(221)1a b c \++=--=-；综上所述：2005()a b c ++的值为1±.【解析】（1）根据解一元一次方程的步骤：去分母——去括号——移项——合并同类项——系数化为1.（2）将4x =代入方程383()2a x a a +=+-解得2a =.（3）根据题意可得2a =，2b =-，1c =±，再分情况求得代数式的值即可.。

人教版七年级数学上册《第四章整式的加减》单元测试卷及答案一、整体代入法求值整体代入法求值，就是将一个复杂的表达式或方程看作一个整体，然后将其代入到另一个表达式或方程中进行求解的方法。

通过“比较各项系数”“拼拆各项构造整体”“比较各项系数”“拼拆各项构造整体”等方法“化繁为简”，将复杂的问题分解成若干个简单的问题，再逐一解决，最终汇聚成整体的答案。

一、 整体代入——比较各项系数1. 若代数式b a -2的值为1 ，则代数式b a 247-+ 的值为( ) .A. 7B. 8C. 9D. 102. 若a 、b 互为相反数，c 、d 互为倒数，则()=-+cd b a 3 .3. 已知代数式y x 2+的值是3 ，则代数式142-+y x 的值是 .4. 若6=+b a ，则=--b a 2218 ( ) .A. 6B. 6-C. 24-D. 125. 已知,0122=++a a 求3422-+a a 的值 . 6. 若72=-b a ，则b a 426+- 的值为 .7. 如果代数式b a -的值为4 ，那么代数式522--b a 的值为 . 8. 已知代数式y x -2的值是2- ，则代数式y x +-21 的值是 .二、 整体代入——拼拆各项构造整体1. 请回答下列各题：（ 1 ）化简：()().363252222y x xy xy y x --+ （ 2 ）化简求值：已知,2,9==+ab b a 求()()⎪⎭⎫ ⎝⎛+--++-b ab a ab ab ab 2141025131532的值.2. 已知,12,5=-=+c b b a 则c b a -+2 的值为( ) . A. 17B. 7C. 17-D.7-3. 已知5=-b a ，2=+d c 则()()d a c b --+的值是( ) .A.3-B. 3C.7-D. 74. 已知3=-b a ，2=+dc 则()()d a c b --+ 的值为 .5. 已知,6,1422-=-=+bc b bc a 则22b a+ 的值是 ，bc b a 3222+-的值是6. 已知,5,14=-=+ab b a 求()()[]a b ab a b ab 65876+--++ 的值 .三、 整体代入——比较各项系数1. 代数式22++x x 的值为0 ，则代数式3222-+x x 的值为( ) . A. 6 B. 7 C. 6- D. 7-2. 解答下列问题：（ 1 ）若代数式7322++x x 的值为 8 ，那么代数式2025962++x x 的值为（ 2 ）若5,7==+xy y x .则代数式xy y x +--228的值为 （ 3 ）若,5,162244=-=+xy y x y x 则()()()422244253y xy xy y x y x----- 的值是多 少？3. 若代数式y x 32-的值是1 ，那么代数式846+-x y 的值是 .4. 已知a ，b 互为相反数， c ，d 互为倒数， x 的绝对值为2 ．求()()20252cd x cd b a x -+++-的值 .5. 已知a 与b 互为相反数，c 与d 互为倒数， m 的值为6-，求m cd mba +-+的值 . 6. 若代数式5322++x x 的值是 8 ，则代数式7642-+x x 的值是( ) . A. 1- B. 1 C. 9- D. 9 7. 若1-=-n m ，则()n m n m 222+-- 的值是 .四、 整体代入——拼拆各项构造整体1. 若32-=+mn m，1832=-mn n 则224n mn m -+ 的值为 .2. 已知2,522-==+ab b a ，求代数式()()222222353242b b ab ab ab a ++---+的值.3. 已知：1,4-==-mn n m .求：()()()mn n m m n mn n m mn ++--+-++-4223322的值 . 4. 已知(),07535172=-++-+y x y x 求=+y x 32 .5. 已知,62,1422-=-=+bc b bc a 则=-+bc b a 54322 ( ) .A. 18B. 18-C. 20D. 86. 已知2-=-+a c b ，则()()=-++⎪⎭⎫ ⎝⎛+-+--a c b c b a c b c b a a 2223132323232 参考答案一、 整体代入——比较各项系数【解答】()b a b a -+=-+227247把12=-b a 代入上式得：927=+=∴原式. 答案：C【解答】b a 、 互为相反数，d c 、互为倒数.,1,0==+∴cd b a(),3303-=-=-+∴cd b a 答案：3-【知识点】倒数的定义1. 【解答】由题意可知：,32=+y x 原式().516122=-=-+=y x【解答】，6=+b a(),612182182218=-=+-=--∴b a b a 答案：A 2. 【解答】，0122=++a a ()550512234222=-=-++=-+∴a a a a3. 【解答】()b a b a 226426--=+-，其中,72=-b a 所以原式8726-=⨯-=4. 【解答】，4=-b a ()35425252=-⨯=--=--b a b a5. 【解答】22-=-y x()()3212121=--=--=+-∴y x y x二、 整体代入——拼拆各项构造整体1.【解答】（1）原式222222913361510xy y x y x xy xy y x +=+-+=（2）原式b ab a ab ab ab 24252210---++-=(),255822524210b a ab ba ab +--=--⎪⎭⎫ ⎝⎛+-+-=其中.2,9==+ab b a.5206511618922558-=--=⨯-⨯-=∴原式 2.【解答】12,5=-=+c b b a()()171252=+=-++=-+∴c b b a c b a .答案：A3.【解答】2,5=+=-d c b a()()325-=+-=++-=+-+=∴d c b a d a c b 原式.答案：A4.【解答】,d a c b +-+=原式()()132-=-=--+=+-+=b a d c ba d c5.【解答】()();86142222=-+=-++=+bc b bc a b a()()();346282322222=--=--+=+-bc bbc abc b a答案：8；346.【解答】()34228=++=++=ab b a a b ab 原式三、整体代入——比较各项系数1. 【解答】2,0222-=+=++x x x x 即()734322-=--=-+=x x 原式.答案：D2. 【解答】（1）87322=++x x,1322=+∴x x则原式(),20282025320253232=+=++=x x（2）,5,7==+xy y x()xy y x ++-=∴28原式151485728-=+-=+⨯-=（3）()()()422244253y xy xy y xyx -----()()115165,16,3225322442244422244=-=∴=-=+∴--+=+-+--=原式xy y x y x xy y x y x y xy xy y x y x3. 【解答】,132=-y x()6828322=+-=+--=∴y x 原式【解答】b a , 互为相反数，d c ,互为倒数，x 的绝对值为2,2,1,0±===+∴x cd b a当2=x 时，原式()()；11241210220252=--=-+⨯+-=当2-=x 时，原式()()()()；51241210220252=-+=-+-⨯+--= 所以()()20252cd x cd b a x -+++-的值为1或5.【解答】b a , 互为相反数0=+∴b ad c , 互为倒数1=∴cd.5610610=+-=-+-=+-+m cd mba 4. 【解答】由题意可知：85322=++x x,3322=+∴x x().1732276422-=-+=-+∴x x x x 答案：A5. 【解答】1-=-n m()()()()()3121222222=-⨯--=---=+-=n m n m nm n m四、整体代入——拼拆各项构造整体1. 【解答】方法一：,183,322=--=+mn n mn m∴将这两个等式的两边相减得：(),183322--=--+mn n mn m,21322-=+-+∴mn n mn m ,21422-=-+∴n mn m方法二：原式(),332222mn n mn m n mn mn m --+=-++= 将183,322=--=+mn n mn m 代入 得原式21183-=--=2.【解答】原式,691524822222b b ab a b ab a +-+--+=(),137,71372222ab b a b ab a ++-=-+-=当2,522-==+ab b a 时 原式612635-=--=.3. 【解答】原式,4223322mn n m m n mn n m mn ---+--++-=(),36336n m mn nm mn -+-=-+-=把1,4-==-mn n m 代入得：原式18126=+=.4. 【解答】 已知条件17-+y x 和()27535-+y x 都是非负数，且(),07535172=-++-+y x y x .3932,5127535170753517=+∴⎩⎨⎧==∴⎩⎨⎧=+=+∴=-+=-+∴y x y x y x y x y x y x5. 【解答】bc b a 54322-+()()182414324322=-⨯=-++=bc b bc a6. 【解答】原式().382323222=⨯=--=c b a。

人教版七年级上册数学第四章《几何图形》单元测试卷（满分100分，时间90分钟）一、选择题（本大题共十小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是正确的.）1.下列说法不正确的是（）A．用一个平面去截一个正方体可能截得五边形B．五棱柱有10个顶点C．沿直角三角形某条边所在的直线旋转一周，所得的几何体为圆柱D．将折起的扇子打开，属于“线动成面”的现象2.下列图形中，经过折叠不能围成一个正方体的是（）A．B．C．D．3.图1是一个正六面体，把它按图2中所示方法切割，可以得到一个正六边形的截面，则下列展开图中正确画出所有的切割线的是（）A．B．C．D．4.已知∠1=27°18′，∠2=27.18°，∠3=27.3°，则下列说法正确的是（）A．∠1=∠3B．∠1=∠2C．∠1＜∠2D．∠2=∠35.如图是顺义区地图的一部分，小明家在怡馨家园小区，小宇家在小明家的北偏东约15°方向上，则小宇家可能住在（）A．裕龙花园三区B．双兴南区C．石园北区D．万科四季花城6.一个正方体的展开图如图所示，将它折成正方体后，数字“0”的对面是（）A．数B．5 C．1 D．学7.如图，∠AOB是一直角，∠AOC=40°，OD平分∠BOC，则∠AOD等于（）A．65°B．50°C．40°D．25°8.数学活动课上，四位同学围绕作图问题：“如图，已知直线l和直线l外一点P，用直尺和圆规作直线PQ，使PQ⊥l于点Q．”分别作出了下列四个图形，其中作法错误的为（）A．B．C．D．9.如图所示，一艘船从A点出发，沿东北方向航行至点B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC的余角是（）A．15°B．30°C．45°D．75°10.某乡镇的4个村庄A,B,C,D恰好位于正方形的4个顶点上，为了解决农民出行难问题，镇政府决定修建连接各村庄的道路系统，使得每两个村庄都有直达的公路，设计人员给出了如下四个设计方案（实线表示连接的道路）在上述四个方案中最短的道路系统是方案（）A．一B．二C．三D．四二、填空题（本大题共10小题，每小题2分，共20分）11.有一正角锥的底面为正三角形.如果这个正角锥其中两个面的周长分别为27,15，则此正角锥所有边的长度和为.12.有3块积木，每一块的各面都涂上不同的颜色，3块的涂法完全相同，现把它们摆放成不同的位置（如图），请你根据图形判断涂成绿色一面的对面的颜色是.13.如图是一个立方体的平面展开图形，每个面上都有一个自然数，且相对的两个面上两数之和都相等，若13,9,3的对面的数分别是a,b,c，则a2+b2+c2﹣ab﹣ac﹣bc的值为.14.用一根长28分米的木条截开后刚好能搭一个长方体的架子，这个长方体的长、宽、高的长度都是整数分米，且都不相等，那么这个长方体的体积等于立方分米.15.经过A,B两点的直线上有一点C，AB=10，CB=6，D和E分别是AB,BC的中点，则DE 的长是.16.上午8：30钟表的时针和分针构成角的度数是.17.下列几何体属于柱体的有个.18.平面内不同的两点确定一条直线，不同的三点最多确定三条直线，平面内不同的七个点最多可确定条直线.19.用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②圆柱；③圆锥；④正三棱柱（写出所有正确结果的序号）.20.已知一个圆柱的侧面展开图是如图所示的矩形，长为6π，宽为4π，那么这个圆柱底面圆的半径为.三、解答题（21 ~23题每题7分，25题8分，26题8分，27题8分）21.如图，点C在线段AB上，AC=6cm，MB=10cm，点M,N分别为AC,BC的中点．（1）求线段BC,MN的长；（2）若C在线段AB的延长线上，且满足AC﹣BC=bcm，M,N分别是线段AC,BC的中点，求MN的长度．22.如图是一个正方体的展开图，标注了字母“a”的面是正方体的正面，已知正方体相对两个面上的代数式的值相等．求a+的值．。

人教版七年级数学上册第四章测试卷及答案解析【含详细知识点】第四章测试卷一、选择题(项)1．下列说法正确的是( ) A ．两点确定一条直线B ．两条射线组成的图形叫作角C ．两点之间直线最短D ．若AB ＝BC ，则点B 为AC 的中点2．如图，长度为18cm 的线段AB 的中点为M ，点C 是线段MB 的一个三等分点，则线段AC 的长为( )A ．3cmB ．6cmC ．9cmD ．12cm第2题图 第3题图3．如图，∠AOB 为平角，且∠AOC ＝27∠BOC ，则∠BOC 的度数是( )A ．140°B ．135°C ．120°D ．40°4．如图是一个正方体纸巾盒，它的平面展开图是( )5．把一副三角尺ABC 与BDE 按如图所示那样拼在一起，其中A ，D ，B 三点在同一直线上，BM 为∠ABC 的平分线，BN 为∠CBE 的平分线，则∠MBN 的度数是( )A ．30°B ．45°C ．55°D ．60°6．如图，线段AB 表示一根对折以后的绳子，现从P 处把绳子剪断，剪断后的各段绳子中最长的一段为8cm.若PB比AP长3cm，则这条绳子的原长为()A．10cm B．26cmC．10cm或22cm D．19cm或22cm二、填空题(本大题共6小题，每小题3分，共18分)7．如图，为抄近路践踏草坪是一种不文明的现象，请你用数学知识解释出现这一现象的原因__________________________．第7题图第8题图8．如图所示的图形中，柱体为__________(请填写你认为正确物体的序号)．9．如图，已知线段AB＝16cm，点M在AB上，AM∶BM＝1∶3，P，Q分别为AM，AB的中点，则PQ的长为________．第9题图第11题图10．往返于甲、乙两地的客车，中途停靠3个车站(来回票价一样)，且任意两站间的票价都不同，共有________种不同的票价，需准备________种车票．11．如图，将三个同样的正方形的一个顶点重合放置，那么∠1的度数为________．12．从点O引出三条射线OA，OB，OC，已知∠AOB＝30°，在这三条射线中，当其中一条射线是另两条射线所组成角的平分线时，则∠AOC的度数为________．三、(本大题共5小题，每小题6分，共30分)13．下列图形中，上面是一些具体的实物，下面是一些立体图形，请找出与下面立体图形相类似的实物，用线连接起来．14．如图，已知A、B、C、D四点，根据下列要求画图：(1)画直线AB、射线AD；(2)画∠CDB；(3)找一点P，使点P既在AC上又在BD上．15．观察下面由7个小正方体组成的图形，请你画出从正面、上面、左面看到的平面图形．16．如图，已知直线AB、CD、EF相交于点O，∠2＝2∠1，∠3＝3∠2，求∠DOE的度数．17．如图，B是线段AD上一点，C是线段BD的中点．(1)若AD＝8，BC＝3，求线段CD，AB的长；(2)试说明：AD＋AB＝2AC.四、(本大题共3小题，每小题8分，共24分)18．已知∠α＝76°，∠β＝41°31′，求： (1)∠β的余角；(2)∠α的2倍与∠β的12的差．19．已知线段AB ＝20cm ，M 是线段AB 的中点，C 是线段AB 延长线上的点，AC ：BC ＝3：1，点D 是线段BA 延长线上的点，AD ＝AB .求：(1)线段BC 的长； (2)线段DC 的长； (3)线段MD 的长．20．如图，将两块直角三角尺的顶点叠放在一起．(1)若∠DCE ＝35°，求∠ACB 的度数； (2)若∠ACB ＝140°，求∠DCE 的度数；(3)猜想∠ACB 与∠DCE 的关系，并说明理由．五、(本大题共2小题，每小题9分，共18分)21．如图，已知点O在线段AB上，点C，D分别是AO，BO的中点．(1)AO＝________CO；BO＝________DO；(2)若CO＝3cm，DO＝2cm，求线段AB的长度；(3)若线段AB＝10，小明很轻松地求得CD＝5.他在反思过程中突发奇想：若点O在线段AB的延长线上，原有的结论“CD＝5”是否仍然成立呢？请帮小明画出图形分析，并说明理由．22．如图，甲、乙两船同时从小岛A出发，甲船沿北偏西20°的方向以40海里/时的速度航行；乙船沿南偏西80°的方向以30海里/时的速度航行．半小时后，两船分别到达B，C两处．(1)以1cm表示10海里，在图中画出B，C的位置；(2)求A处看B，C两处的张角∠BAC的度数；(3)测出B，C两处的图距，并换算成实际距离(精确到1海里)．六、(本大题共12分)23．定义：从一个角的顶点出发，把这个角分成1∶2的两个角的射线，叫作这个角的三分线，显然，一个角的三分线有两条．例如：如图①，若∠BOC＝2∠AOC，则OC是∠AOB 的一条三分线．(1)已知：如图①，OC是∠AOB的一条三分线，且∠BOC＞∠AOC，若∠AOB＝60°，求∠AOC的度数；(2)已知：∠AOB＝90°，如图②，若OC，OD是∠AOB的两条三分线．①求∠COD的度数；②现以O为中心，将∠COD顺时针旋转n°得到∠C′OD′，当OA恰好是∠C′OD′的三分线时，求n的值．参考答案与解析1．A2．D3．A4．B5．B6．C7．两点之间，线段最短8．①②③⑥9．6cm10．102011. 20°12．15°或30°或60°解析：①如图①，当OC平分∠AOB时，∠AOC＝12∠AOB＝15°；②如图②，当OA平分∠BOC时，∠AOC＝∠AOB＝30°；③如图③，当OB平分∠AOC时，∠AOC＝2∠AOB＝60°.故答案为15°或30°或60°.13．解：如图所示．(6分)14．解：如图所示．(6分)15．解：图略．(6分)16．解：∵∠2＝2∠1，∴∠1＝12∠2.(1分)∵∠3＝3∠2，∴∠1＋∠2＋∠3＝12∠2＋∠2＋3∠2＝180°，解得∠2＝40°，(4分)∴∠3＝3∠2＝120°，∴∠DOE ＝∠3＝120°.(6分)17．解：(1)∵C 是线段BD 的中点，BC ＝3，∴CD ＝BC ＝3.∴AB ＝AD －BC －CD ＝8－3－3＝2.(3分)(2)∵AD ＋AB ＝AC ＋CD ＋AB ，BC ＝CD ，∴AD ＋AB ＝AC ＋BC ＋AB ＝AC ＋AC ＝2AC .(6分)18．解：(1)∠β的余角＝90°－∠β＝90°－41°31′＝48°29′.(3分)(2)∵∠α＝76°，∠β＝41°31′，∴2∠α－12∠β＝2×76°－12×41°31′＝152°－20°45′30″＝131°14′30″.(8分)19．解：(1)设BC ＝x cm ，则AC ＝3x cm.又∵AC ＝AB ＋BC ＝(20＋x )cm ，∴20＋x ＝3x ，解得x ＝10.即BC ＝10cm.(2分)(2)∵AD ＝AB ＝20cm ，∴DC ＝AD ＋AB ＋BC ＝20＋20＋10＝50(cm)．(5分)(3)∵M 为AB 的中点，∴AM ＝12AB ＝10cm ，∴MD ＝AD ＋AM ＝20＋10＝30(cm)．(8分)20．解：(1)由题意知∠ACD ＝∠ECB ＝90°，∴∠ACB ＝∠ACD ＋∠DCB ＝∠ACD ＋∠ECB －∠DCE ＝90°＋90°－35°＝145°.(3分)(2)由(1)知∠ACB ＝180°－∠DCE ，∴∠DCE ＝180°－∠ACB ＝40°.(5分)(3)∠ACB ＋∠DCE ＝180°.(6分)理由如下：∵∠ACB ＝∠ACD ＋∠DCB ＝90°＋90°－∠DCE ＝180°－∠DCE ，∴∠ACB ＋∠DCE ＝180°.(8分)21．解：(1)2 2(2分)(2)∵点C ，D 分别是AO ，BO 的中点，CO ＝3cm ，DO ＝2cm ，∴AO ＝2CO ＝6cm ，BO ＝2DO ＝4cm ，∴AB ＝AO ＋BO ＝6＋4＝10(cm)．(5分)(3)仍然成立，如图：理由如下：∵点C ，D 分别是AO ，BO 的中点，∴CO ＝12AO ，DO ＝12BO ，(7分)∴CD＝CO －DO ＝12AO －12BO ＝12(AO －BO )＝12AB ＝12×10＝5(cm)．(9分)22．解：(1)图略．(3分)(2)∠BAC ＝90°－80°＋90°－20°＝80°.(6分) (3)约2.3cm ，即实际距离约23海里．(9分)23．解：(1)∵OC 是∠AOB 的一条三分线，且∠BOC ＞∠AOC ，∴∠AOC ＝13∠AOB＝13×60°＝20°.(3分) (2)①∵∠AOB ＝90°，OC ，OD 是∠AOB 的两条三分线，∴∠BOC ＝∠AOD ＝13∠AOB＝13×90°＝30°，∴∠COD ＝∠AOB －∠BOC －∠AOD ＝90°－30°－30°＝30°.(6分) ②分两种情况：当OA 是∠C ′OD ′的三分线，且∠AOD ′＞∠AOC ′时，如图①，∠AOC ′＝13∠C ′OD ′＝10°，∴∠DOC ′＝∠AOD －∠AOC ′＝30°－10°＝20°，∴∠DOD ′＝∠DOC ′＋∠C ′OD ′＝20°＋30°＝50°；(9分)当OA 是∠C ′OD ′的三分线，且∠AOD ′＜∠AOC ′时，如图②，∠AOC ′＝20°，∴∠DOC ′＝∠AOD －∠AOC ′＝30°－20°＝10°，∴∠DOD ′＝∠DOC ′＋∠C ′OD ′＝10°＋30°＝40°.综上所述，n ＝40或50.(12分)第四章走进图形世界知识点详细梳理1、几何图形：现实生活中的物体我们只管它的形状、大小、位置而得到的图形，叫做几何图形从实物中抽象出来的各种图形，包括立体图形和平面图形。

初一上册第四章测试卷一、选择题（每题3分，共30分）1. 下列关于有理数的说法中，正确的是（）A. 有理数就是整数B. 有理数包括正数和负数C. 有理数是整数和分数的统称D. 0不是有理数答案：C。

解析：有理数是整数和分数的统称，整数只是有理数的一部分，A错误；有理数包括正有理数、负有理数和0，B不全面；0是有理数，D错误。

2. 计算 - 3+5的结果是（）A. - 2B. 2C. 8D. - 8答案：B。

解析：异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值，5的绝对值大于3的绝对值，5 - 3 = 2。

3. 一个数的相反数是 - 7，这个数是（）A. - 7B. 7C. 1/7D. - 1/7答案：B。

解析：互为相反数的两个数和为0，设这个数为x，则x+( - 7)=0，解得x = 7。

4. 若 x = 3，则x的值为（）A. 3B. - 3C. 3或 - 3D. 9答案：C。

解析：绝对值为3的数有两个，3和 - 3。

5. 化简 - (- 2)的结果是（）A. - 2B. 2C. 1/2D. - 1/2答案：B。

解析：负负得正，所以 - (- 2)=2。

6. 单项式 - 3x²y的系数是（）A. - 3B. 3C. - 3x²D. - 3y答案：A。

解析：单项式中的数字因数叫做单项式的系数，所以- 3x²y的系数是 - 3。

7. 多项式2x² - 3x+1的次数是（）A. 2B. 3C. 1D. 0答案：A。

解析：多项式的次数是多项式中次数最高的项的次数，在2x² - 3x + 1中，2x²的次数最高，为2。

8. 计算2a+3a的结果是（）A. 5aB. 6aC. aD. 1答案：A。

解析：同类项相加，字母和指数不变，系数相加，2 + 3 = 5，所以2a+3a = 5a。

9. 方程3x - 1 = 5的解是（）A. x = 2B. x = 3C. x = 4/3D. x = 1/3答案：A。

人教版数学7年级上册第4单元·时间：120分钟满分：120分班级__________姓名__________得分__________一、选择题（共12小题，满分36分，每小题3分）1．（3分）（2022秋•榕城区校级月考）圆柱的截面不可能是（ ）A．梯形B．长方形C．正方形D．椭圆2．（3分）（2022秋•南岗区校级月考）如果长方体的长、宽、高都扩大3倍，则它的体积扩大（ ）倍．A．3B．9C．6D．273．（3分）（2022秋•南岗区校级月考）一个长方体的棱长之和是180厘米，相交于一个顶点的三条棱的长度和是（ ）A．45厘米B．30厘米C．90厘米D．60厘米4．（3分）（2022秋•南岗区校级月考）一个长方体水箱，从里面量长5分米，宽和高都是2分米，现在往这个水箱倒入15升水，水箱（ ）A．倒满了B．还没倒满C．溢出来了D．无法确定5．（3分）（2022秋•和平区校级月考）如图，AB＝12cm，C为AB的中点，点D在线段AC上且AD：CB＝1：3，则DB的长是（ ）A．8cm B．10cm C．12cm6．（3分）（2022秋•天桥区校级月考）用纸片和小棒做成下面的小旗，快速旋转小棒，所形成的图形正确顺序是（ ）A．①②③④B．③④①②C．①③②④D．④②①③7．（3分）（2021秋•萨尔图区校级期末）甲、乙两人要从学校回家，他们分别选择了①、②两条路线，比较一下，所走的路程是（ ）A ．①条长B ．②条长C ．一样长D ．无法确定8．（3分）（2022秋•聊城月考）下列各选项中的图形绕虚线旋转一周后，得到的几何体是圆柱的是（ ）A ．B ．C ．D ．9．（3分）（2021秋•乌当区期末）如图，点O 在直线AB 上，射线OD 是∠AOC的平分线，若∠COB ＝40°，则∠DOC 的度数是（ ）A ．20°B ．45°C ．60°D ．70°10．（3分）（2021秋•萨尔图区校级期末）一个圆锥的体积是12立方厘米，底面积是4平方厘米，高是（ ）厘米．A ．3B ．6C ．9D ．1211．（3分）（2022春•东营期末）如图，OC 平分∠AOB ，OD 平分∠BOC ，下列各式正确的是（ ）A ．∠COD =12∠AOBB ．∠BOD =12∠AODC ．∠BOC =23∠AOD D ．∠AOD =23∠AOB 12．（3分）（2022•南京模拟）如图，已知B ，C 是线段AD 上任意两点，E是AB 的中点，F 是CD 的中点，下列结论不正确的是（ ）A．AC＝CD B．AB＝2AECD D．BC＝EF﹣AE﹣FDC．CF=12二、填空题（共6小题，满分18分，每小题3分）13．（3分）（2021秋•栾城区期末）如图，∠AOB＝∠COD＝90°，则∠AOC ∠BOD（选填“＞”、“＝”或“＜”）．14．（3分）（2022秋•新城区校级月考）如图，将一个装了一半水的密闭圆柱形玻璃杯水平放置时，水面的形状是 ．15．（3分）（2022秋•柳江区月考）如图，把6个形状、大小完全相同的长方形如图摆放，面积共是12平方单位，则阴影部分的面积是 平方单位．16．（3分）（2021秋•萨尔图区校级期末）一个体积是60立方厘米的圆柱，削成一个最大的圆锥体，这个圆锥的体积是 cm3．17．（3分）（2022春•沂水县期中）如图，AB与CD相交于点O，OE是∠AOC 的平分线，且OA恰好平分∠EOD，则∠AOC＝ 度．18．（3分）（2022春•岚山区期末）如图，将一张宽度相等的纸条折叠，折叠后的一边与原边的夹角是140°，则∠α的度数是 ．三、解答题（共7小题，满分66分）19．（9分）（2022秋•新城区校级月考）已知一个直棱柱，它有27条棱，其中一条侧棱长为20，底面各边长都为5．（1）这是几棱柱？（2）它有多少个面？多少个顶点？（3）这个棱柱的所有侧面的面积之和是多少？20．（9分）（2022秋•昭阳区校级月考）如图，经测量，B处在A处的南偏西56°的方向，C处在A处的南偏东17°方向，C处在B处的北偏东78°方向，求∠C的度数．21．（9分）（2022秋•高州市校级月考）如图所示的五棱柱的底面边长都是5cm，侧棱长12cm，它有多少个面？它有多少条棱？它有多少个顶点？它的所有侧面的面积之和是多少？22．（9分）（2021秋•萨尔图区校级期末）求阴影部分的面积．23．（10分）（2022秋•萍乡月考）如图所示是一个多面体的展开图形，每个面（外表面）都标注了字母，请你根据要求回答问题：（1）这个多面体是什么常见几何体；（2）如果B 在前面，C 在左面，那么哪一面在上面．24．（10分）（2022•丰顺县校级开学）如图1，把一张长10cm 、宽6cm 的长方形纸板分成两个相同的直角三角形（圆锥的体积公式为V 圆锥=13πr 2ℎ，π取3.14）．（1）甲三角形（如图2）旋转一周，可以形成一个怎样的几何体？它的体积是多少立方厘米？（2）乙三角形（如图3）旋转一周，可以形成一个怎样的几何体？它的体积是多少立方厘米？25．（10分）（2022春•钢城区期末）如图，点C 是线段AB 上的一点，点M是线段AC 的中点，点N 是线段BC 的中点．（1）如果AB ＝14cm ，AM ＝5cm ，求BC 的长；（2）如果MN ＝8cm ，求AB 的长．参考答案一、选择题（共12小题，满分36分，每小题3分）1．A2．D3．A4．B5．B6．B7．C8．C9．D10．C11．C12．A二、填空题（共6小题，满分18分，每小题3分）13．＝14．长方形15．816．2017．12018．70°三、解答题（共7小题，满分66分）19．【解答】解：（1）∵此直棱柱有27条棱，∴由27÷3＝9，可知此棱柱是九棱柱；（2）这个九棱柱有11个面，有18个顶点；（3）这个棱柱的所有侧面的面积之和是5×9×20＝900．20．【解答】解：由题意得：∠ABC＝78°﹣56°＝22°，∠BAC＝56°+17°＝73°，∴∠C＝180°﹣∠ABC﹣∠BAC＝180°﹣22°﹣73°＝85°，∴∠C 的度数为85°．21．【解答】解：如图，它有7个面，15条棱，10个顶点，所有侧面的面积之和为：5×12×5＝300（cm 3）．答：它有7个面，15条棱，10个顶点，它的所有侧面的面积之和是300cm 3．22．【解答】解：阴影部分的面积为：90°360°×π×(42)2=π（cm 2）．23．【解答】解：（1）根据多面体的展开图形可知，多面体是长方体；（2）根据长方体及其表面展开图的特点可知，面“B ”与面“D ”相对，面“E ”与面“A ”相对，面“C ”与面“F ”相对，如果B 在前面，C 在左面，则E 在下面，A 在上面．24．【解答】解：（1）甲三角形旋转一周可以形成一个圆锥，它的体积是 13×3.14×62×10=376.8(cm 3)．（2）乙三角形旋转一周可以形成一个圆柱，里面被挖去一个圆锥，它的体积是 3.14×62×10―13×3.14×62×10=753.6(cm 3)．25．【解答】解：（1）∵点M 是线段AC 的中点，AM ＝5cm ，∴AC ＝2AM ＝10cm ，∵AB ＝14cm ，∴BC ＝AB ﹣AC ＝14﹣10＝4cm ；（2）∵点M 是线段AC 的中点，点N 是线段BC 的中点，∴NC =12BC ，CM =12AC ，∴MN ＝NC +CM =12（BC +AC ）=12AB ，∵MN ＝8cm ，∴12AB ＝8，∴AB ＝16cm ．。

2023年人教版七年级数学上册第四章几何图形初步单元测试卷及答案七年级数学·上时间：90分钟满分：120分一、选择题(每题3分，共30分)1．下列几何体中，是圆锥的为()2．【2021·百色】已知∠α＝25°30′，则它的余角为()A．25°30′ B．64°30′ C．74°30′ D．154°30′3．下列作图语句错误．．的是()A．延长线段ABB．延长射线ABC．直线m和直线n相交于点PD．在射线AB上截取线段AC，使AC＝3 cm4．下列立体图形中，都是柱体的为()5．如图，表示∠1的其他方法中，不正确．．．的是()A．∠ACBB．∠CC．∠BCAD．∠ACD6．如图所示的几何体从上面看到的图形为()17．在下列生活、生产现象中，不可以用基本事实“两点确定一条直线”来解释的有()①平板弹墨线②建筑工人砌墙③会场摆直茶杯④弯河道改直A．1个B．2个C．3个D．4个8．【教材P138例4变式】如图，在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的度数为()A．69°B．111°C．141°D．159°9．在直线上顺次取A，B，C三点，使得AB＝5 cm，BC＝3 cm，如果O是线段BC的中点，那么线段AO的长度是()A．8 cm B．7.5 cm C．6.5 cm D．2.5 cm 10．如图，点A，B是正方体的两个顶点，将正方体按如下方式展开，则在展开图中点A，B的位置标注正确的是()二、填空题(每题3分，共24分)11．【2020·广州】已知∠A＝100°，则∠A的补角等于________．12．七棱柱有________个面，________个顶点．13．【教材P130习题T10改编】已知线段AB＝8 cm，在直线AB上画线段BC，使2它等于3 cm，则线段AC＝______________.14．用“度、分、秒”表示21.24°为__________．15．【教材P136例1变式】【中考·大连】如图，点O在直线AB上，射线OC平分∠BOD，若∠COB＝35°，则∠AOD等于________．(第15题)(第17题)(第18题)16．【教材P134练习T1改编】钟表在8：25时，时针与分针的夹角是________度．17．如图是由一些相同的小正方体搭成的几何体从正面、左面、上面看到的形状图，则搭成这个几何体的小正方体的个数是________．18．如图，将一副三角尺叠放在一起，使直角顶点重合于O，则∠AOC＋∠DOB ＝________.三、解答题(19～22题每题10分，其余每题13分，共66分)19．【教材P128练习T2改编】如图，已知线段a，b，画一条线段，使它等于3a －b(用直尺和圆规画图，不要求写画法)．20．一个角的余角比它的补角的13还少20°，求这个角的度数．3421．一个几何体从三个方向看到的图形如图所示(单位：cm)． (1)写出这个几何体的名称：__________；(2)若其从上面看为正方形，根据图中数据计算这个几何体的体积．22．如图，点C 是AB 的中点，D ，E 分别是线段AC ，CB 上的点，且AD ＝23AC ，DE ＝35AB .若AB ＝24 cm ，求线段CE 的长．23．如图，OD 平分∠BOC ，OE 平分∠AOC ，∠BOC ＝60°，∠AOC ＝58°.(1)求∠AOB的度数．(2)①求∠DOC和∠ADE的度数；②判断∠DOE与∠AOB是否互补，并说明理由．24．已知在同一平面内，∠AOB＝90°，∠AOC＝60°.(1)∠COB＝____________．(2)若OD平分∠BOC，OE平分∠AOC，则∠DOE的度数为________．(3)在(2)的条件下，将题目中的∠AOC＝60°改成∠AOC＝2α(α＜45°)，其他条件不变，你能求出∠DOE的度数吗？若能，请写出求解过程；若不能，说明理由.5答案一、1.B 2.B 3.B 4.C 5.B 6.C7.A8．C9.C10.A二、11.80°12.9；1413.11 cm或5 cm14．21°14′24″15.110°16.102.517.518.180°点思路：根据角的和差关系，将∠AOC表示为∠AOD＋∠COD，则∠AOC＋∠DOB＝∠AOD＋∠DOB＋∠COD＝∠AOB＋∠COD＝90°＋90°＝180°.三、19.解：如图，AE＝3a－b .20．解：设这个角的度数为x.依题意得90°－x＋20°＝13(180°－x)，解得x＝75°.答：这个角的度数为75°. 21．解：(1)长方体(2)体积为3×3×4＝36(cm3)．22．解：因为点C是AB的中点，所以AC＝BC＝12AB＝12×24＝12(cm)．所以AD＝23AC＝23×12＝8(cm)．所以CD＝AC－AD＝12－8＝4(cm)．因为DE＝35AB＝35×24＝14.4(cm)，所以CE＝DE－CD＝14.4－4＝10.4(cm)．23．解：(1)∠AOB＝∠BOC＋∠AOC＝60°＋58°＝118°.(2)①因为OD平分∠BOC，OE平分∠AOC，所以∠DOC＝∠BOD＝12∠BOC＝12×60°＝30°，∠AOE＝∠COE＝12∠AOC＝12×58°＝29°.6②∠DOE与∠AOB不互补．理由：因为∠DOC＝30°，∠COE＝29°，所以∠DOE＝∠DOC＋∠COE＝59°.所以∠DOE＋∠AOB＝59°＋118°＝177°.所以∠DOE与∠AOB不互补．24. 点易错：本题根据题目条件解答时，OC是在∠AOB内部，还是在∠AOB外部，其位置不确定，且它们都符合条件，因此解答本题应分OC在∠AOB 外部和内部两种情况讨论.解：(1)30°或150°(2)45°(3)能求出∠DOE的度数．需要分两种情况讨论：①当OC在∠AOB内部时，如图①所示．因为OD平分∠BOC，OE平分∠AOC，所以∠COD＝12∠BOC ，∠COE＝12∠AOC.所以∠DOE＝∠COD＋∠COE＝12∠BOC＋12∠AOC＝12(90°－2α)＋12·2α＝45°.②当OC在∠AOB外部时，如图②所示．因为OD平分∠BOC，OE平分∠AOC，所以∠COD＝12∠BOC，∠COE＝12∠AOC.所以∠DOE＝∠COD－∠COE＝12∠BOC－12∠AOC＝12(90°＋2α)－12·2α＝45°.综上所述，∠DOE的度数是45°.78。