2017年秋季新版北师大版九年级数学上学期4.2、平行线分线段成比例同步练习6

2017年九年级数学上4.2 平行线分线段成比例（北师大版）2 平行线分线段成比例1．理解平行线分线段成比例定理．(重点)2．会用平行线分线段成比例定理解决问题．(难点) 阅读教材P82～84，自学“例题”，完成下列内容：(一)知识探究基本事实：两条直线被一组________所截，所得的对应线段成比例．推论：平行于三角形一边的直线与其他两边相交，截得的对应线段________．(二)自学反馈如图，l1、l2分别被l3、l4、l5所截，且l3∥l4∥l5，则(1)ABBC＝（）（）；(2)ABDE＝（）（）＝（）（）；(3)AB（）＝（）DF.活动1 小组讨论例如图，在△ABC中，E，F分别是AB和AC上的点，且EF∥BC.(1)如果AE＝7，EB＝5，FC＝4，那么AF的长是多少？(2 )如果AB＝10，AE＝6，AF＝5，那么FC的长是多少？解：(1)∵EF∥BC，∴AEEB＝AFFC.∵AE＝7，EB＝5，FC＝4，∴AF＝AEFCEB＝7×45＝2(2)∵EF∥BC，∴AEAB＝AFAC.∵AB＝10，AE＝6，AF＝5，∴AC＝ABAFAE＝10×56＝2∴FC＝AC－AF＝253－5＝103.本例是平行线分线段成比例的推论的简单应用，为后面证明相似三角形的判定定理做铺垫．注意对“截得的对应线段”中“截得”的理解，同时找准对应线段是关键．活动2 跟踪训练1．如图，△ABC中，D、E分别在AB、AC上，且DE∥BC，若AE∶EC＝1∶2，AD＝6，则AB的长为( ) A．18 B．12C．9 D．32．如图，已知在△ABC中，点D，E，F分别是边AB，AC，BC上的点，DE∥BC，EF∥AB，且AD∶DB＝3∶5，那么CF∶FB＝( )A．5∶8 B．3∶．3∶5 D．5∶33．如图，l1∥l2∥l3，直线a，b与l1、l2、l3分别相交于A、B、C和点D、E、F.若ABBC＝23，DE＝4，则EF 的长是________．4．如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F，ABBC＝23，DE＝6，则EF＝________.5．如图，已知：△ABC中，DE∥BC，AD＝3，DB＝6，AE ＝2，求AC的长．6．如图所示，如果D，E，F分别在OA，OB，OC上，且DF∥AC，EF∥BC.求证：OD∶OA＝OE∶OB.活动3 课堂小结平行线分线段成比例定理：(1)两条直线被一组平行线所截，所得的对应线段成比例．(2)平行于三角形一边的直线与其他两边相交，截得的对应线段成比例．【预习导学】(一)知识探究平行线成比例(二)自学反馈(1)DE EF (2)BC EF AC DF (3)AC DE【合作探究】活动2 跟踪训练1．A 2.D 3.6 ．∵DE∥BC，∴ADBD＝AEEC.∵AD ＝3，DB＝6，AE＝2，∴36＝2EC.解得EC＝4.∴AC＝AE＋EC＝6. 6.证明：∵DF∥AC，∴ODOA＝OFOC.∵EF∥BC，∴OFOC＝OEOB.∴ODOA＝OEOB。

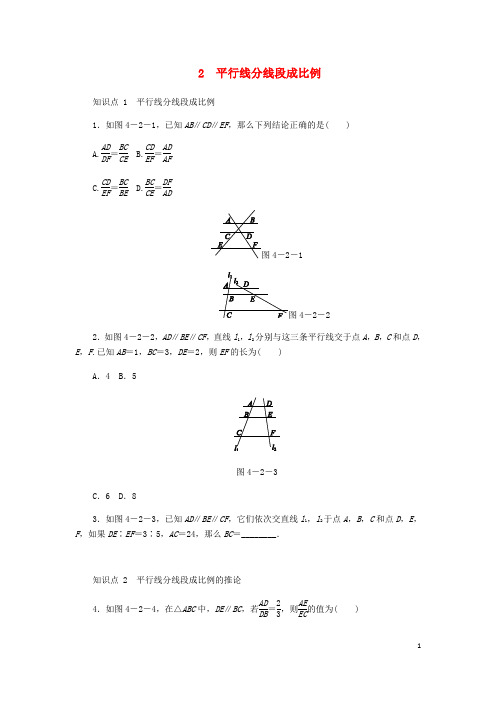
2 平行线分线段成比例知识点 1 平行线分线段成比例1．如图4－2－1，已知AB ∥CD ∥EF ，那么下列结论正确的是( )A.AD DF ＝BC CEB.CD EF ＝AD AFC.CD EF ＝BC BE D.BC CE ＝DF AD4－2－14－2－22．如图4－2－2，AD ∥BE ∥CF ，直线l 1，l 2分别与这三条平行线交于点A ，B ，C 和点D ，E ，F .已知AB ＝1，BC ＝3，DE ＝2，则EF 的长为( )A ．4B ．5图4－2－3C ．6D ．83．如图4－2－3，已知AD ∥BE ∥CF ，它们依次交直线l 1，l 2于点A ，B ，C 和点D ，E ，F ，如果DE ∶EF ＝3∶5，AC ＝24，那么BC ＝________．知识点 2 平行线分线段成比例的推论4．如图4－2－4，在△ABC 中，DE ∥BC ，若AD DB ＝23，则AE EC的值为( )A.13B.25C.23D.354－2－44－2－55．如图4－2－5，在△ABC 中，DE ∥BC ，AD ＝6，DB ＝3，AE ＝4，则EC 的长为( )A ．1B ．2C ．3D ．46．如图4－2－6，已知△ABC 中，DE ∥BC ，AD ＝5，EC ＝2，BD ＝AE ＝x ，求BD 的长．图4－2－67．如图4－2－7，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE ∥BC ，EF ∥AB .若AD ＝2BD ，则CF BF的值为( ) A.12 B.13 C.14 D.234－2－74－2－88．如图4－2－8，在△ABC中，AB＞AC，AD是BC边上的高，F是BC的中点，EF⊥BC 交AB于点E，若BD∶DC＝3∶2，则BE∶AB＝________．9．如图4－2－9，在△ABC中，DG∥EC，EG∥BC.求证：AE2＝AB·AD.图4－2－9详解1．A2．C [解析] 本题考查平行线分线段成比例基本事实的运用．∵AD ∥BE ∥CF ，∴AB BC ＝DE EF .又∵AB ＝1，BC ＝3，DE ＝2，∴EF ＝BC ·DE AB＝6. 3．15 [解析] ∵AD ∥BE ∥CF ，∴AB BC ＝DE EF ＝35. ∵AC ＝24，∴BC ＝24×58＝15. 故答案为15.4．C5．B [解析] ∵DE ∥BC ，∴AD DB ＝AE EC ，即63＝4EC ，解得EC ＝2. 故选B.6．解：∵DE ∥BC ，∴AD BD ＝AE EC ， ∴5x ＝x 2，∴x 2＝10， ∴x ＝10或x ＝－10(不合题意，舍去)，∴BD ＝10.7．A [解析] 由DE ∥BC ，EF ∥AB ，AD ＝2BD ，得AD BD ＝AE EC ＝2，AE EC ＝BF CF ＝2，∴CF BF ＝12.故选A.8．5∶6[解析] ∵AD是BC边上的高，EF⊥BC，∴AD∥EF.又∵F是BC的中点，且BD∶DC＝3∶2，∴BF∶FD＝5∶1.再根据平行线分线段成比例基本事实，得BE∶EA＝BF∶FD＝5∶1，即BE∶AB＝5∶6.9．证明：∵DG∥EC，∴AD∶AE＝AG∶AC.∵EG∥BC，∴AG∶AC＝AE∶AB，∴AD∶AE＝AE∶AB，即AE2＝AB·AD.。

度第一学期北师大版九年级数学上册_42_平行线分线段成比例_同步课堂检测题4.2 平行线分线段成比例同步课堂检测题考试总分： 100 分考试时间： 90分钟学校：__________ 班级：__________ 姓名：__________ 考号：__________一、选择题（共 10 小题，每小题 3 分，共 30 分）1.已知：如图，l1 // l2 // l3，则在下列比例中一定成立的是（）A.llll =llllB.llll=llllC.llll =llllD.llll=llll2.如图，已知ll // ll // ll，那么下列结论不正确的是（）A.llll =llllB.llll=llllC.llll =llllD.llll=llll3.如图，在△lll中，点l，l，l分别在边ll，ll，ll上，若ll // ll，ll // ll，则下面所列比例式中正确的是（）A.llll =llllB.llll=llllC.llll =llllD.llll=llll4.如图，直线l1 // l2 // l3，直线ll分别交l1，l2，l3于点l，l，l，直线ll分别交l1，l2，l3于点l，l，l，已知ll=2，ll=5，ll=6，则ll的长是（）A.3B.125C.185D.525.如图，△lll中，ll // ll，ll=2，ll=4，ll=6，则ll的长是（）第1页/共8页A.2B.3C.4D.56.如图，点l 、l 分别在梯形llll 的两腰ll 、ll 上，且ll // ll ，若ll =12，ll =18，ll :ll =3:2，则ll 的值为（ ） A.15.6B.15C.19D.无法计算7.如图，已知l 1 // l 2 // l 3，如果ll :ll =2:3，ll =4，则ll 的长是（ ） A.103B.6C.4D.258.如图，在△lll 中，ll // ll ，ll =6，ll =3，ll =4，则ll 的长为（ ） A.1B.2C.3D.49.如图的矩形llll 中，l 点在ll 上，且ll <ll ．若l 、l 两点分别在ll 、ll 上，ll :ll =4:1，ll :ll =4:1，直线ll 交ll 于l 点，且l 、l 两点到ll 的距离分别为l 、l ，则下列关系何者正确？（ ） A.l <l ，ll =ll B.l <l ，ll <ll C.l =l ，ll =llD.l =l ，ll <ll10.已知线段l ，l ，l ，求作线段l ，使l =ll l，下列作法中正确的是（ ） A.B.C.D.二、填空题（共 10 小题 ，每小题 3 分 ，共 30 分 ）11.如图，直线l 1、l 2、l 3分别交直线l 4于点l 、l 、l，交直线l5于点l、l、l，且l1 // l2 // l3．如果ll=5，ll=7，ll=6，那么ll=________．12.已知：如图，ll // ll，ll=5，ll=6，ll=8，则ll=________．13.如图，直线l // l // l，点l是线段ll的中点，若ll=2，则ll=________．14.如图所示，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆．小丽站在离南岸边15米的点l处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且在这两棵树之间还有三棵树，则河宽为________米．15.在四边形llll中，l是对角线ll上的一点，ll // ll，ll // ll，求llll +llll=________．16.如图，在△lll中，ll // ll // ll，ll=ll，ll=14，ll=5，那么ll=________．17.如图，在6×6的正方形网格中，连结两格点l，l，线段ll与网格线的交点为l、l，则ll:ll:ll为________．18.如图，△lll中，ll // ll，ll=1，ll=2，ll=2，那么ll=________．19.如图，直线l // l // l，度量线段ll≈1.89，ll≈3.80，ll≈2.02，则线段ll的长约为________．20.如图，己知点l在△lll的ll边上，点l在ll边上．ll:ll=2:5，ll=14厘米，当ll的长等于________厘米第3页/共8页时，可以证得ll // ll．三、解答题（共 5 小题，每小题 8 分，共 40 分）21.如图，在△lll中，llll=90∘，ll是斜边ll上的高，llll的平分线交ll于点l，llll的平分线交ll于点l，连接ll．求证：ll // ll．22.如图，已知梯形llll中，ll // ll，ll，ll交于l，过l作ll的平行线交ll于l，交ll于l．若ll=3ll，ll=5ll，求ll．23.如图，已知l1 // l2 // l3，两条直线交于点l，且与这三条平行线分别交于点l、l、l和l、l、l，若ll=2，ll=3，ll= 1，ll=4，求ll的长．24.已知△lll中，ll // ll，l、l分别在ll、ll上，ll、ll交于点l，ll交ll于点l，求证：ll=ll．25.如图，在△lll中，点l为ll上一点，点l在ll上，过点l作ll // ll交ll于点l，作ll // ll交ll于点l．(1)若点l是ll的中点，且ll:ll=2:1，求ll:ll的值；(2)若点l是ll的中点，试证明llll =llll；(3)若点l是ll上任意一点，试证明llll +llll=llll．答案1.B2.B3.C4.B5.D6.A7.B8.B9.D10.D11.30712.20313.214.22.515.116.1917.1:3:218.419.4.0420.421.解：∵llll的平分线交ll于点l，∵ll ll =llll，∵llll的平分线交ll于点l，∵ll ll =llll，∵ll是斜边ll上的高，第5页/共8页∵llll=llll=90∘，∵llll+llll=90∘，而llll+llll=90∘，∵llll=llll，∵ll△lll∽ll△lll，∵ll ll =llll，∵ll ll =llll，∵ll ll =llll，∵ll // ll．22.解：∵ll // ll，ll // ll，∵ll // ll // ll，∵ll // ll，∵ll ll =llll∵，∵ll // ll，∵ll ll =llll∵，∵+∵得llll +llll=llll+llll=1，即ll3+ll5=1，∵ll=158．23.解：∵l2 // l3，∵ll ll =llll，即llll+3=14，∵ll=1，∵ll=ll−ll=2−1=1．24.解：∵ll // ll，∵ll ll =llll，llll=llll，llll=llll，llll=llll，∵ll ll =llll，llll=llll，∵ll ll =llll，∵ll=ll．25.解：(1)过点l作ll // ll交ll于l，∵点l为ll中点，∵点l是ll中点，且llll =llll，∵ll ll =ll2ll=13；(2)延长ll至点l，使ll=ll，连ll、ll，则四边形llll是平行四边形．∵ll // ll，ll // ll，∵ll ll =llll，llll=llll∵ll ll =llll；（注：像第(1)题那样作辅助线也可以．）(3)过点l作ll // ll交ll于l，∵ll ll =llll，又∵ll // ll，∵ll // ll∵ll ll =llll，∵ll ll =llll×llll=llll×llll第7页/共8页同理可得：llll =llll×llll∵ll ll +llll=llll×(llll+llll)=llll．（注：如果像第(2)题那样添辅助线，也可以证．）。

4.2 平行线分线段成比例一．选择题1．如图，直线a，b，c被直线l1，l2所截，交点分别为点A，C，E和点B，D，F．已知a ∥b∥c，且AC＝3，CE＝4，则的值是（）A．B．C．D．2．如图，在△ABC中，EF∥BC，，则＝（）A．B．C．D．3．如图，AB∥CD∥EF，若BF＝3DF，则的值是（）A．B．2C．D．34．如图，若l1∥l2∥l3，且＝，则正确的是（）A．＝B．＝C．＝D．＝5．如图，在△ABC，D是BC上一点，BD：CD＝1：2，E是AD上一点，DE：AE＝1：2，连接CE，CE的延长线交AB于F，则AF：AB为（）A．1：2B．2：3C．4：3D．4：76．如图，AB∥CD∥MN，点M，N分别在线段AD，BC上，AC与MN交于点E，则（）A．＝B．＝C．＝D．＝7．如图，在△ABC中，DE∥BC，∠ADE＝∠EFC，AE：EC＝5：3，BF＝10，则CF的长为（）A．16B．8C．4D．68．如图，在△ABC中，DE∥BC，EF∥AB，则下列结果正确的是（）A．＝B．＝C．＝D．＝9．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．＝B．＝C．＝D．＝10．如图，DE∥BC，DF∥AC，那么下列比例式中正确的是（）A．＝B．＝C．＝D．＝11．如图，AB∥CD∥EF，AD＝4，BC＝DF＝3，则BE的长为（）A．B．C．4D．612．如图，在△ABC中，点D、E、F分别是边AB、AC、BC上的点，DE∥BC，EF∥AB，且AD：DB＝3：5，那么CF：CB等于（）A．3：8B．3：5C．5：8D．2：513．△ABC中，F是AC的中点，D、E三等分BC、BF与AD、AE分别交于P、Q，则BP：PQ：QF＝（）A．5：3：2B．3：2：1C．4：3：1D．4：3：214．如图所示，AD是△ABC的中线，E是AD上一点，AE：ED＝1：3，BE的延长线交AC 于F，AF：AC＝（）A．1：4B．1：5C．1：6D．1：715．如图，AD是△ABC的中线，E是AC边上一点，且CE：AE＝1：2，BE交AD于点F，则AF：FD为（）A．5：1B．4：1C．3：1D．2：116．如图AB∥CD∥EF，AF、BE相交于O，若AO＝OD＝DF＝3cm，BE＝10cm，则BO的长为（）A．cm B．5cm C．cm D．3cm二．解答题17．如图，已知AC∥FE∥BD，求证：+＝1．18．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝60°，AC＝6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．（1）求线段DE的长；（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求的值．19．如图，BD∥直线m，求证：PM•PN＝PR•PS．20．如图，点C是线段AB上的任意一点（C点不与A、B点重合），分别以AC、BC为边在直线AB的同侧作等边三角形△ACD和等边三角形BCE，AE与CD相交于点M，BD 与CE相交于点N．（1）求证：MN∥AB；（2）若AB的长为10cm，当点C在线段AB上移动时，是否存在这样的一点C，使线段MN的长度最长？若存在，请确定C点的位置并求出MN的长；若不存在，请说明理由．21．如图，已知在△ABC中，EF∥CD，AF＝3，AD＝5，AE＝4．（1）求CE的长；（2）当AB＝时，求证：DE∥BC．22．已知：如图所示，直线AE、BD、CF相交于点O，AC∥EF，BC∥DF，求证：AB∥DE．参考答案与试题解析一．选择题1．解：∵a∥b∥c，∴，∴，故选：C．2．解：∵EF∥BC，∴，又∵，∴＝，故选：C．3．解：∵AB∥CD∥EF，∴，故选：B．4．解：∵l1∥l2∥l3，且＝，∴＝，∴＝；故选：C．5．解：过D作DH∥AB交CF于H，如图，∵DH∥BF，∴＝，∵BD：CD＝1：2，∴CD：BC＝2：3，∴BF＝DH，∵DH∥AF，∴＝＝2，∴AF＝2DH，∴AF：BF＝2DH：DH＝4：3，∴AF：AB＝4：7．故选：D．6．解：∵ME∥CD，∴＝，∴＝．故选：D．7．解：∵DE∥BC，∴∠ADE＝∠B，∵∠ADE＝∠EFC，∴∠B＝∠EFC，∴EF∥AB，∴＝，∵AE：EC＝5：3，BF＝10，∴＝，解得：CF＝6，故选：D．8．解：∵DE∥BC，EF∥AB，∴＝，故A选项错误；＝＝，故B选项错误；＝，故C选项错误；＝，故D选项正确．故选：D．9．解：A、∵DE∥BC，EF∥AB，∴＝，正确；B、∵DE∥BC，EF∥AB，∴，正确；C、∵DE∥BC，EF∥AB，∴，错误；D、∵DE∥BC，EF∥AB，∴，正确；故选：C．10．解：∵DF∥AC，∴＝，∵DE∥BC，∴＝，∴＝．故选：C．11．解：∵AB∥CD∥EF，∴＝，又∵AD＝4，BC＝DF＝3，∴＝，∴CE＝，∴BE＝BC+CE＝3+＝．故选：B．12．解：∵DE∥BC，EF∥AB，∴AE：EC＝AD：DB＝BF：CF＝3：5，∴CF：CB＝5：8，故选：C．13．解：过F作FN∥BC，交AE于M，AD于N，∵F为AC中点，∴FM是△AEC中位线，∴MF＝CE，CE＝2FM，∵BD＝DE＝CE，∴BE＝2CE＝4FM，∵FM∥BC，∴△FMQ∽△BEQ，∴＝＝，∵FN是△ADC的中位线，∴FN＝CD＝CE＝BD，∵FN∥BC，∴△FNP∽△BDP，∴＝＝1，∴BP＝PF，∵＝，∴＝，∴FQ＝BF，∵BP＝BF，FQ＝BF，∴PQ＝PF﹣QF＝BF﹣BF＝BF，∴BP：PQ：QF＝（BF）：（BF）：（BF）＝5：3：2．故选：A．14．解：作DH∥BF交AC于H∵AD是△ABC的中线，∴BD＝DC，∴FH＝HC，∵DH∥BF，∴∴AF：FC＝1：6，∴AF：AC＝1：7，故选：D．15．解：过D作DG∥AC交BE于G，∵AD是△ABC的中线，∴DG＝又AE＝2EC，∴AF：FD＝AE：DG＝2EC：EC＝4：1．故选：B．16．解：AB∥CD∥EF，AF，BE相交于O，AO＝OD＝DF，∴由B平行线等分线段定理得：OB＝OC＝CE，∴BO＝BE＝，故选：A．二．解答题17．证明：∵AC∥EF，∴，∵FE∥BD，∴，①+②，得：，即．18．解：（1）∵AD平分∠BAC，∠BAC＝60°，∴∠DAC＝30°，在Rt△ACD中，∠ACD＝90°，∠DAC＝30°，AC＝6，∴CD＝2，在Rt△ACB中，∠ACB＝90°，∠BAC＝60°，AC＝6，∴BC＝6，∴BD＝BC﹣CD＝4，∵DE∥CA，∴，∴DE＝4；（2）如图，∵点M是线段AD的中点，∴DM＝AM，∵DE∥CA，∴，∴DF＝AG，∵DE∥CA，∴，∴，∵BD＝4，BC＝6，DF＝AG，∴．19．证明：∵BD∥直线m，∴＝，＝，∴＝，∴＝，∵BD∥直线m，∴＝，＝，∴＝，∴＝，∴＝，∴PM•PN＝PR•PS．20．（1）证明：∵△ACD与△BCE是等边三角形，∴AC＝CD，CE＝BC，∴∠ACE＝∠BCD，在△ACE与△DCB中，∵，∴△ACE≌△DCB（SAS），∴∠CAE＝∠BDC，在△ACM与△DCN中，∵，∴△ACM≌△DCN，∴CM＝CN，又∵∠MCN＝180°﹣60°﹣60°＝60°，∴△MCN是等边三角形，∴∠MNC＝∠NCB＝60°即MN∥AB；（2）解：假设符合条件的点C存在，设AC＝x，MN＝y，∵MN∥AB，∴＝，即＝，y＝﹣（x﹣5）2+2.5（0＜x＜10），当x＝5时，y max＝2.5cm．21．解：（1）∵EF∥CD，∴＝，∵AF＝3，AD＝5，AE＝4，∴＝，解得：AC＝，∵AE＝4，∴CE＝AC﹣AE＝﹣4＝；（2）∵AB＝，AD＝5，AE＝4，AC＝，∴＝＝，∵∠A＝∠A，∴△ADE∽△ABC，∴∠ADE＝∠B，∴DE∥BC．22．证明：∵AC∥EF，∴＝，∵BC∥DF，∴＝，∴＝，∵∠AOB＝∠DOE，∴AB∥DE．。

《第二节 平行线分线段成比例》提升训练1.（教材P85习题T4变式）（上海中考）如图，在△ABC 中，点D ，E ，F 分别是边AB ，AC ，BC 上的点，DE ∥BC ，EF ∥AB ，且AD ：DB =3：5，那么CF ：CB 等于( )A .5：8B .3：8C .3：5D .2：52.（梧州中考）如图，AG ：GD =4：1，BD ：DC =2：3，则AE ：EC 的值是( )A .3：2B .4：3C .6：5D .8：53.如图，直线1l ∥2l ∥3l ，AB =3，AD =2，DE =4，EF =7.5. 求BC ，BE 的长.4.如图，点F 是□ABCD 的边CD 上一点，连接BF 并延长交AD 的延长线于点E . 求证：DEDFAE DC .5.（南阳淅川县模拟）如图，在△ABC中，EF∥CD，DE∥BC.（1）求证：AF：FD=AD：DB；（2）若AB=15，AD：BD=2：1，求DF的长.链接河南中招6.（河南模拟）如图，在横格作业纸（横线等距）上一画条直线，与横格线交于A，B，C三点，则BC：AC等于( )A.2：3B.2：5C.3：4D.3：5微专题5作平行线转换线段的比【方法指导】求线段的比，通常利用平行线分线段成比例的基本事实及其推论得到比例线段，然后进行转化得到所求两条线段的比；遇到不能直接转化线段的比时，要联想到借助辅助线（作平行线）构造基本图形：A型与X型针对训练（郑州期中）如图，在△ABC中，AD是BC边上的中线，E在AC边上，且AE：EC=1：2，BE交AD于点P，则AP：PD等于( )A.1：1B.1：2C.2：3D.4：3【变式】如图，△ABC中，D在BC上，F是AD的中点，连接CF并延长交AB于点E，已知32CDBD=，则AEBE== .拔高题如图，△ABC中，AF:FD=1：3，BD=DC，求AE:EC的值.参考答案1.A2.D3.解:∵1l ∥2l ∥3l ，∴FB AB AD BE BC DE ==，即324BF BE BC ==.∴BC =6,BF =12BE . 又∵EF =BF +BE =7.5.∴12BE +BE =7.5. ∴BE =5. 4.证明:∵四边形ABCD 是平行四边形，∴CD ∥AB ，AD ∥BC . ∴DE EF AE EB =. 同理可得EF DF EB DC =.∴DE DF AE DC=. 5.解:（1）证明:∵EF ∥CD ，∴AF AE FD EC =. ∵DE ∥BC ，∴AD AE BD EC =. ∴AF AD FD BD=，即AF ∶FD =AD ∶DB . （2）103DF =6.C微专题 5针对训练 A变式 35拔高题解: 过点D 作DG ∥BE 交AC 于G ，则AF :FD =AE ：EG =1：3，BD ：CD =EG :CG = 1 ：1，所以AE :EC =1：6.。

平行线分线段成比例一、选择题(每小题6分，共18分)1．如图，已知DE ∥BC ，EF ∥AB ，则下列比例式中错误的是（ ）A.AD AB ＝AE AC B ．CE CF ＝EA FB C.DE BC ＝AD BDD ．EF AB ＝CF CB第1题图2．(2015·乐山)如图，l 1∥l 2∥l 3，两条直线与这三条平行线分别交于点A ，B ，C和D ，E ，F ，已知AB BC ＝32，则DEDF的值为（ ）A.32B ．23C.25 D ．35第2题图 3．(2016·兰州)如图，在△ABC 中，DE ∥BC ，若AD DB ＝23，则AEEC等于（ ）A.13 B ．25 C.23D ．35二、填空题(每小题6分，共18分)4．如图，已知AB ∥DE ，AE 与DB 交于点C ，AC ＝3，BD ＝5，CD ＝3，则CE ＝____.5．如图，已知AB ∥CD ∥EF ，AC ∶CE ＝2∶3，BF ＝15，那么BD ＝___.6．如图所示，AD 是△ABC 的中线，F 是AD 上一点，CF 的延长线交AB 于点E ，若AF ∶FD ＝1∶3，则AE ∶AB ＝___.三、解答题(共64分)7．(满分18分)已知，如图，DE ∥AB ，FD ∥BC ，AD AC ＝23，AB ＝9 cm ，BC ＝6 cm ，求平行四边形BEDF 的周长．8．(满分24分)已知，如图，在△ABC 中，∠ACB 的平分线CD 交AB 于点D ，过点B 作BE ∥CD 交AC 的延长线于点E .(1)求证：BC ＝CE ；(2)求证：AD DB ＝ACCB.9．(满分22分)已知：如图，在平行四边形ABCD 中，E 是BA 边延长线上一点，CE 交对角线DB 于点G ，交AD 边于点F . 求证：CG 2＝GF ·GE .参考答案1.C2.D3.C解析：因为DE ∥BC ，所以AD ∶DB ＝AE ∶EC ，∴AE EC ＝AD DB ＝23.4.5解析：∵AB ∥DE ，AC ＝3，BD ＝5，CD ＝3, BC ＝5－3＝2， CE AC ＝CD BC ，即CE 3＝32， ∴CE ＝4.5. 5.6_解析：∵AB ∥CD ∥EF ，AC ∶CE ＝2∶3，BF ＝15，∴AC CE ＝BD DF ＝23， ∴BD15－BD ＝23，∴BD ＝6.6.1∶7.解析：如图，过点D 作DG ∥CE ，交AB 于点G ， ∵AF ∶FD ＝1∶3，∴AF AD ＝14，又∵D 是BC 的中点，∴EC ＝2DG ，∴EF DG ＝AF AD ＝14，∴EF ＝14DG ，∴AE AG ＝AF AD ＝14，∴AG ＝4AE ，∴EG ＝BG ＝3AE ，∴AB ＝7AE ， ∴AE ∶AB ＝1∶7.7.解：∵FD ∥BC ，AD AC ＝23，∴AF AB ＝AD AC ＝23，∴AF 9＝23， ∴AF ＝6 cm ，∴BF ＝9－6＝3(cm)，又∵DE ∥AB ，∴CD AC ＝CE BC ＝13，∴13＝CE6，∴CE ＝2(cm)， ∴BE ＝4 cm ，∴平行四边形BEDF 的周长为14 cm. 8.证明：(1)∵CD 平分∠ACB ， ∴∠ACD ＝∠BCD . 又∵BE ∥CD ，∴∠CBE ＝∠BCD ，∠CEB ＝∠ACD . ∴∠CBE ＝∠CEB . 故△BCE 是等腰三角形， ∴BC ＝CE ；(2)∵BE ∥CD ，根据平行线分线段成比例定理可得：AD DB ＝AC CE ，又∵BC ＝CE ，∴AD DB ＝ACCB.9.证明：∵四边形ABCD 是平行四边形， ∴DC ∥AB ，AD ∥BC ，∵DC ∥AB ，∴CG GE ＝DGGB，∵AD ∥BC ，∴CG GF ＝BG DG ，∴CG GF ＝GECG，即CG 2＝GF ·GE .。

2 平行线分线段成比例知识点 1 平行线分线段成比例1．如图4－2－1，若l 1∥l 2∥l 3，则下列各式不一定成立的是( )图4－2－1A.AC CE ＝BD DFB.BD AC ＝DF CEC.AC AE ＝BD BFD.AE AC ＝EF CD2．教材习题4.3第1题变式题如图4－2－2，AD ∥BE ∥CF ，直线l 1，l 2分别与这三条平行线交于点A ，B ，C 和点D ，E ，F.已知AB ＝1，BC ＝3，DE ＝2，则EF 的长为( )图4－2－2A ．4B ．5C ．6D ．83．如图4－2－3，AB ∥CD ∥EF ，AF 与BE 相交于点G ，且AG ＝2，GD ＝1，DF ＝5，那么BCCE的值为________．图4－2－34．如图4－2－4，已知AD ∥BE ∥CF ，它们分别交直线l 1，l 2于点A ，B ，C 和点D ，E ，F.如果DE ∶EF ＝3∶5，AC ＝24，那么BC ＝________．图4－2－45．已知：如图4－2－5，直线l 1∥l 2∥l 3，AB ＝3，BC ＝5，DF ＝12.求DE 和EF 的长．图4－2－5知识点 2 平行线分线段成比例的推论6．如图4－2－6，在△ABC 中，DE ∥BC ，若AD DB ＝23，则AEEC的值为( )图4－2－6A.13B.25C.23D.357．教材习题4.3第2题变式题如图4－2－7，在△ABC 中，DE ∥BC ，AD ＝6，DB ＝3，AE ＝4，则EC 的长为( )图4－2－7A ．1B ．2C ．3D ．48．如图4－2－8，△ABC 中，DE ∥BC ，AD AB ＝13，AE ＝2 cm ，则AC 的长是( )图4－2－8A ．2 cmB ．4 cmC ．6 cmD ．8 cm9．如图4－2－9，已知AB ∥CD ，AD 与BC 相交于点O.若BO ∶OC ＝2∶3，AD ＝10，则AO ＝________.图4－2－910．如图4－2－10，已知在△ABC 中，DE ∥BC ，AD ＝5，EC ＝2，BD ＝AE ＝x ，求BD 的长．图4－2－1011．如图4－2－11，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE ∥BC ，EF ∥AB.若AD ＝2BD ，则CFBF的值为( )图4－2－11A.12B.13C.14D.2312．已知线段a ，b ，c ，求作线段x 使ax ＝bc ，下列每个图中的两条虚线都是平行线，则作法正确的是( )图4－2－1213．如图4－2－13，在△ABC中，AB＞AC，AD是BC边上的高，F是BC的中点，EF ⊥BC交AB于点E，若BD∶DC＝3∶2，则BE∶AB＝________．图4－2－1314．如图4－2－14，AB∥CD，AD与BC相交于点O，若AO＝2，DO＝4，BO＝3，求BC的长．图4－2－1415．教材习题4.3第4题变式题如图4－2－15，在△ABC中，D，E，F分别是AB，AC，BC上的点，且DE∥BC，DF∥AC，AE∶EC＝3∶4，BC＝21，求BF的长．图4－2－1516．如图4－2－16，已知AC∥EF∥BD，求证：AEAD＋BEBC＝1.图4－2－16教师详解详析1．D2．C [解析] 本题考查平行线分线段成比例基本事实的运用． ∵AD ∥BE ∥CF ，∴AB BC ＝DEEF .又∵AB ＝1，BC ＝3，DE ＝2， ∴EF ＝BC ·DEAB ＝6.3.354．15 [解析] ∵AD ∥BE ∥CF ，∴AB BC ＝DE EF ＝35.∵AC ＝24，∴BC ＝24×58＝15.故答案为15.5．解：∵直线l 1∥l 2∥l 3，∴AB ∶BC ＝DE ∶EF . ∵AB ＝3，BC ＝5，DF ＝12， ∴3∶5＝DE ∶(12－DE )， ∴DE ＝4.5，∴EF ＝12－4.5＝7.5. 6．C7．B [解析] ∵DE ∥BC ，∴AD DB ＝AE EC ，即63＝4EC ，解得EC ＝2.故选B.8．C [解析] ∵DE ∥BC ，∴AD AB ＝AE AC .∵AD AB ＝13，AE ＝2 cm ，∴2AC ＝13，解得AC ＝6(cm)． 9．410．解：∵DE ∥BC ，∴AD BD ＝AE EC ，∴5x ＝x2，∴x 2＝10，∴x ＝10或x ＝－10(不合题意，舍去)，∴BD ＝10.11．A [解析] 由DE ∥BC ，EF ∥AB ，AD ＝2BD ，得AD BD ＝AE EC ＝2，AE EC ＝BF CF ＝2，∴CFBF ＝12.故选A. 12．A [解析] ∵ax ＝bc ，∴a ∶b ＝c ∶x ，则由图可知只有A 符合题意．故选A. 13．5∶6 [解析] ∵AD 是BC 边上的高，EF ⊥BC ，∴AD ∥EF .又∵F 是BC 的中点，且BD ∶DC ＝3∶2，∴BF ∶FD ＝5∶1.再根据平行线分线段成比例基本事实，得BE ∶EA ＝BF ∶FD ＝5∶1，即BE ∶AB ＝5∶6.14．解：∵AB ∥CD ，∴BO CO ＝AODO .∵AO ＝2，DO ＝4，BO ＝3， ∴3CO ＝24，解得CO ＝6， ∴BC ＝BO ＋CO ＝3＋6＝9.15．解：∵DE ∥BC ，∴AD DB ＝AE EC ＝34.∵DF ∥AC ，∴CF BF ＝AD DB ＝34，∴BC －BF BF ＝34， 即21－BF BF ＝34，解得BF ＝12. 16．证明：∵AC ∥EF ∥BD ， ∴AE AD ＝AF AB ，BE BC ＝BF AB， ∴AE AD ＋BE BC ＝AF AB ＋BF AB ＝AB AB＝1.。

2 平行线分线段成比例一、选择题1．若a b ＝c d ，则下列各式一定成立的是( )． A.a ＋b b ＝c ＋d c B.a ＋c c ＝b ＋d dC.a －c c ＝b －d bD.a －c a ＝b －d d2．如图，已知AB ∥CD ∥EF ，那么下列结论正确的是( )．A.AD DF ＝BC CEB.BC CE ＝DF ADC.CD EF ＝BC BED.CD EF ＝AD AF3．如图所示，在△ACE 中，B 、D 分别在AC 、AE 上，下列推理不正确的是( )．A ．BD ∥CE ⇒AB AC ＝BD CE B ．BD ∥CE ⇒AD AE ＝BD CEC ．BD ∥CE ⇒AB BC ＝AD DE D ．BD ∥CE ⇒AB BC ＝BD CE4．如图所示，AD 是△ABC 的中线，E 是CA 边的三等分点，BE 交AD 于点F ，则AF ∶FD 为( )．A ．2∶1B ．3∶1C ．4∶1D ．5∶15．某同学的身高1.6米，由路灯下向前步行4米，发现自己的影子长2米，则这个路灯的高为( )．A ．4.8米B ．3.2米C ．0.8米D ．2米6．已知E 是ABCD 的边AB 的延长线上的一点，且32DC BE =，则AD BF=( )． A ．3∶2 B ．2∶3 C ．5∶2 D ．2∶5二、填空题7．如图所示，已知a ∥b ，AF BF ＝35，BC CD ＝3，则AE ∶EC ＝________.8．如图所示，已知DE ∥BC ，BF ∶EF ＝3∶2，则AC ∶AE ＝________， AD ∶DB ＝________.三、解答题9．已知AD 是△ABC 的内角平分线，求证：BD DC ＝AB AC .．10．如图所示，已知△ABC 中，AE ∶EB ＝1∶3，BD ∶DC ＝2∶1，AD 与CE 相交于F ，求EF FC ＋AF FD 的值．2平行线分线段成比例一、选择题1.B2.A3.D4.C5.A6.C二、填空题7．125 8. 3∶2 2∶1三、解答题9. 证明 过C 作CE ∥AD 交BA 的延长线于E ，如图所示， 则∠AEC ＝∠BAD ，∠DAC ＝∠ACE .又∠BAD ＝∠DAC ，∴∠AEC ＝∠ACE ，∴AC ＝AE ，又由AD ∥CE 知AB AE ＝BD DC ，∴BD DC ＝AB AC .10. 解 过点D 作DG ∥AB 交EC 于G ，则DG BE ＝CD BC ＝CG EC ＝13，而AE BE ＝13，即AE BE ＝DG BE ，所以AE ＝DG ，从而有AF ＝DF ，EF ＝FG ＝CG ，故EF FC ＋AF FD ＝EF 2EF ＋AF AF ＝12＋1＝32.。

4.2平行线分线段成比例同步测试一．选择题1．如图，点D，E分别在△ABC的边AB，AC上，且DE∥BC，若AD＝2，DB＝3，AC＝10，则AE等于（）A．3B．4C．5D．62．如图，已知AB∥CD∥EF，BD：DF＝1：2，那么下列结论中，正确的是（）A．AC：AE＝1：3B．CE：EA＝1：3C．CD：EF＝1：2D．AB：EF＝1：2 3．如图，l1∥l2∥l3，AB＝2，BC＝4，DB＝3，则DE的长为（）A．4B．5C．6D．94．如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F，若，则的值为（）A．B．C．D．5．如图，直线l1∥l2∥l3，若AB＝6，BC＝9，EF＝6，则DE＝（）A．4B．6C．7D．96．如图，已知AB∥CD∥EF，BD：DF＝2：5，那么下列结论正确的是（）A．AC：EC＝2：5B．AB：CD＝2：5C．CD：EF＝2：5D．AC：AE＝2：5 7．如图，AB∥CD∥MN，点M，N分别在线段AD，BC上，AC与MN交于点E．则下列说法正确的是（）A．B．C．D．8．如图，点D，E，F分别在△ABC的各边上，且DE∥BC，DF∥AC，若AE：EC＝1：2，BF＝6，则DE的长为（）A．1B．2C．3D．49．如图，AB∥CD，AE∥FD，AE、FD分别交BC于点G、H，则下列结论中错误的是（）A．B．C．D．10．如图，已知DE∥BC，EF∥AB，则下列比例式中错误的是（）A．＝B．＝C．＝D．＝二．填空题11．如图，AB∥CD∥EF，点C、D分别在BE、AF上，如果BC＝6，CE＝9，AF＝10，那么DF的长为．12．如图，已知AB∥CD∥EF，AD＝6，DF＝3，BC＝7，那么线段CE的长度等于．13．如图，D是BC的中点，M是AD的中点，BM的延长线交AC于N，则AN：NC＝．14．如图，在△ABC中，D在AC边上，AD：DC＝1：2，O是BD的中点，连接AO并延长交BC于E，则BE：EC＝．15．如图，△ABC中，DE∥BC，G为BC上一点，连接AG交DE于F，已知AD＝3、AB ＝8、FG＝4，则AG＝．三．解答题16．如图，直线l1∥l2∥l3，AC分别交l1，l2，l3于点A，B，C；DF分别交l1，l2，l3于点D，E，F；AC与DF交于点O．已知DE＝3，EF＝6，AB＝4．（1）求AC的长；（2）若BE：CF＝1：3，求OB：AB．17．已知：如图，在△ABC中，点M为AC边的中点，点E为AB上一点，且AB＝4AE，连接EM并延长交BC的延长线于点D，求证：BC＝2CD．18．如图，直线PQ经过菱形ABCD的顶点C，分别交边AB和AD的延长线于点P和Q，BP＝AB，求证：DQ＝2AB．参考答案1．解：∵DE∥BC，∴＝，即＝，解得AE＝4．故选：B．2．解：∵AB∥CD∥EF，BD：DF＝1：2，∴AC：AE＝1：3，故A选项正确；CE：EA＝2：3，故B选项错误；CD：EF的值无法确定，故C选项错误；AB：EF的值无法确定，故D选项错误；故选：A．3．解：∵l1∥l2∥l3，∴，即，解得BE＝6，∴DE＝DB+BE＝3+6＝9，故选：D．4．解：∵l1∥l2∥l3，∴＝＝．故选：C．5．解：∵直线l1∥l2∥l3，∴＝，即＝，∴DE＝4．故选：A．6．解：∵AB∥CD∥EF，∴AC：EC＝BD：DF＝2：5，AC：AE＝BD：BF＝2：7．故选：A．7．解：A、∵AB∥CD∥MN，∴＝，本选项结论不正确；B、∵AB∥CD∥MN，∴＝，本选项结论不正确；C、∵AB∥CD∥MN，∴＝，＝，∴≠，本选项结论不正确；D、∵AB∥CD∥MN，∴＝，本选项结论正确；故选：D．8．解：∵DE∥BC，DF∥AC，∴四边形BDEF为平行四边形，∴DE＝CF，∵DE∥BC，∴＝，∵AE：EC＝1：2，∴AE：AC＝1：3，∴＝，∴DE＝3．故选：C．9．解：A、∵AB∥CD，∴＝，故本选项不符合题目要求；B、∵AE∥DF，∴△CEG∞△CDH，∴＝，∴＝，∵AB∥CD，∴＝，∴＝，∴＝，∴＝，故本选项不符合题目要求；∵AB∥CD，AE∥DF，∴四边形AEDF是平行四边形，∴AF＝DE，∵AE∥DF，∴，∴＝，故本选项不符合题目要求；D、∵AE∥DF，∴△BFH∞△BAG，∴，故本选项符合题目要求；故选：D．10．解：A、∵DE∥BC，EF∥AB，∴＝，正确；B、∵DE∥BC，EF∥AB，∴，正确；C、∵DE∥BC，EF∥AB，∴，错误；D、∵DE∥BC，EF∥AB，∴，正确；故选：C．11．解：∵AB∥CD∥EF，∴＝，∴＝，∴DF＝6，故答案为：6．12．解：∵AB∥CD∥EF，AD＝6，DF＝3，BC＝7，∴，即，解得：CE＝，故答案为：13．解：作DE∥BN交AC于E，∵DE∥BN，M是AD的中点，∴N是AE的中点，∵DE∥BN，D是BC的中点，∴E是NC的中点，∴AN：NC＝1：2，故答案为：1：2．14．解：作DF∥AE交BC于F，如图，∵OE∥DF，∴＝＝1，即BE＝EF，∵DF∥AE，∴＝＝，∴CF＝2EF，∴BE：EC＝BE：3BE＝1：3．故答案为1：3．15．解：∵DE∥BC，∴，即，∴AF＝，∴AG＝AF+FG＝+4＝，故答案为：．16．解：（1）∵l1∥l2∥l3，∴，即，解得：AC＝12；（2）∵l1∥l2∥l3，∴，∵AB＝4，AC＝12，∴BC＝8，∴OB＝2，∴．17．证明：作CF∥DE，交AB于F，如图，∵ME∥CF，∴＝，而M为AC边的中点，∴AM＝MC，∴AE＝EF，∵AB＝4AE，∴EF ＝AB，BF ＝AB，∴BF＝2EF，∵CF∥DE，∴＝＝2，∴BC＝2CD；18．证明：∵菱形ABCD，∴BC∥AD，AB＝DA＝BC＝CD，显然，BC∥QA，又∵，∴＝，∵AB＝AD，∴，∴DQ＝2AB．11 / 11。