人教版九年级数学上册导学案：《圆》第1节 圆周角导学案2

课题:24.1.1圆导学目标：1.经历圆的有关概念的形成过程，理解圆的描述定义和集合概念.2.理解弧、弦、半圆、直径等有关概念，了解等圆、等弧的概念.导学过程：一、欣赏圆二、描绘圆1．圆规画圆；2．借助于现有工具画圆；3．体育老师如何在操场画圆？三、描述圆我们用圆规画圆时，把圆规的一个脚固定，另一个脚绕着它转动一周就画出了一个圆（如图1）．由此，我们可以得到圆的定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做__________.（如图2），固定的端点O叫_________（确定圆的位置）．线段OA叫做_________ （确定圆的大小）．以点O为圆心的圆，记作__________，读作________．（1）（2）四、领会圆问题1：图上各点到定点（圆心O）的距离有什么规律？⊙O上所有的点到O点的距离均等于_______________．问题2：到定点的距离等于定长的点又有什么特点？到O点的距离都等于r的点都在__________ 上.所以说：圆心为O，半径为r的圆可以看成是所有到定点O 的距离_________ 定长r的点组成的图形．用集合的观点定义圆：到定点的距离等于定长的点的集合叫做_________．五、应用圆1.如图，已知点P、Q，且PQ=4cm..P Q （1）画出下列图形：到点P的距离等于2cm的点的集合；到点Q的距离等于3cm的点的集合.（2）在所画的图中，到点P的距离等于2cm，且到点Q 的距离等于3cm的点有几个？请在图中将它们表示出来.图(2)D CBA BDA CBDA C图(1)图(3)（3）在所画的图形中，到点P 的距离小于或等于2cm ，且到点Q 的距离大于或等于3cm 的点的集合是怎么样的图形？把它画出来.2.如图（1），四边形ABCD 是矩形，那么点A 、B 、C 、D 在同一个圆上吗？你能说明理由吗？变题1：如图（2），四边形ABCD 中，∠A =∠C =90°，上述结论是否成立？为什么？变题2：如图（3），若点A 、C 在直线BD 的同侧，∠A =∠C =90°，上述结论还成立吗？为什么？六、研究圆： 与圆有关的概念1.如图，A 、B 、C 是⊙O 上的三个点，且A 、O 、B在同一直线上，我们通过右图认识与圆有关的概念．弦：连接圆上任意两点的_________叫做弦(如图中的AC、AB).直径：经过圆心的________ 叫做直径(如图中的AB).弧：圆上任意两点间的________ 叫做圆弧，简称弧，以A、B为端点的弧记作_______，读作“_______”或“_______”.半圆：圆的任意一条_______ 的两个端点把圆分成两条弧，每一条弧都叫做半圆，半圆是一种特殊的弧.优弧、劣弧：大于_______ 的弧叫做优弧（如图中的_______），小于_______ 的弧叫做劣弧(如图中_______)，优弧、劣弧都是弧，但是优弧大于半圆，劣弧小于半圆．（优弧必须用三个字母表示）2.在同圆或等圆中，能够互相_______的弧叫做等弧，能够_______ 的两个圆叫做等圆.七、自主评价八、回顾反思，深化提高经过一节课的合作探究，你对圆的相关知识又多了解了多少？又学到哪些方法或数学思想，与大家交流一下.4.对角线互相垂直的四边形的各边的中点是否在同一个圆上？并说明理由.【自主评价】1.到定点O 的距离为2cm 的点的集合是以 为圆心， 为半径的圆.2.如图1，点A O D 、、以及点B O C 、、则圆中有 条弦.3．已知⊙O 中最长的弦为16cm ，则⊙O 的半径为____ cm. 4.下列说法正确的是 （填序号）①直径是弦 ②弦是直径 ③半径是弦 ④半圆是弧，但弧不一定是半圆⑤半径相等的两个半圆是等弧 ⑥长度相等的两条弧是等弧 ⑦等弧的长度相等5.如图2，在ABC ∆中，90,40,ACB A ∠=︒∠=︒以C 为圆心，CB 为半径的圆交AB 于点D ，求ACD ∠的度数．（图2）（图1）6．如图，矩形ABCD的对角线AC和BD相交于O点，E、F、G、H分别为OD、OA、OB、OC的中点，试说明E、F、G、H四个点在以点O为圆心、OE为半径的同一个圆上。

初中-数学-打印版24.1.4《圆周角》（2）学习目标1．认识圆内接四边形，理解并掌握圆内接四边形的性质. 2．灵活运用圆的性质解决相关问题. 学习重点：圆内接四边形及其性质. 学习难点: 运用圆的性质解决相关问题. 学习过程 一．自主学习1．如图1，AB 是⊙O 的直径，C 是⊙O 上任一点，你能确定∠ACB 的度数吗?为什么？ 2．如图2，圆周角∠BCA =90º，弦AB 经过圆心O 吗？为什么？ 我们还可以得到圆周角定理的推论：在_______或______中，如果两个______相等，那么_____________一定相等。

半圆（或直径）所对的圆周角是_______，90°的圆周角所对的弦是________.图1 3．如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做__________________；这个圆叫做________________.4．思考：圆内接四边形的对角有什么关系？为什么？ 这样，我们利用圆周角定理，得到圆内接四边形的一个性质：______________________. 二．探索新知思考1 你能设法确定一个圆形纸片的圆心吗？说说你有多少种方法？思考2 如果三角形一边上的中线等于这条边的一半，那么这个三角形是_____三角形。

请证明这个结论.三．应用新知例1 如图，⊙O 的直径AB 为10cm ，弦AC 为6cm ，∠ACB 的平分线交⊙O 于点D ， (1)求BC 、BD 、AD 的长。

(2)求CD 的长。

例2 已知：如图，在△ABC 中，AB=AC ，以AB 为直径的圆O 交BC 于点D ，交AC 于点E ，（1）求证： BD = DE ；（2）连接BE ，如果BC=6，AB=5，求BE 的长．O ED CB A OC B A图3O D C B A E OCA B初中-数学-打印版四．发现总结1．解决圆周角的问题时常根据_______所对的圆周角是______作为依据，添加辅助线构造______三角形.2．求三角形的高的常用方法有哪些？ 五．巩固提高如图，点D 为Rt △ABC 斜边AB 上的一点，以CD 为直径的圆分别交△ABC 三边于点E 、F 、G三点，连EF 、FG.（1）求证：∠EFG =∠B ； （2）若AC=2BC=54，D 为AE 的中点，求CD 的长.六．课堂检测1．如图1，若AB 是⊙0的直径，CD 是⊙O 的弦，∠ABD=58°， 则∠BCD=（ ） A.116° B.32° C.58° D.64°2．如图2，⊙O 的直径AB=13，弦AC=5，∠ACB 的平分线交⊙O 于D ，则CD 的 长（ ） A. 7 B. 9 C.2217D. 29 3．如图3，四边形ABCD 是圆内接四边形，E 是BC 延长线上一点，若∠BAD ＝105°，则∠DCE=____________.4．如图4，AB 是半圆O 的直径，D 为 AC 的中点，∠B=40°，求∠C 的度数为________.图1 图2 图3 图45．如图，AB 为⊙O 的直径，点Q 在弦BC 的延长线上，且∠PCQ =∠PCA. （1）求证：PA=PB ； （2）求PCBC AC 的值.6．如图，BC 为⊙O 的直径，F 是半圆上异于B 、C 的一点，A 是弧BF 的中点，AD ⊥BC ，垂足为D ，BF 交AD 于点E.O ABD CDG E FB AC Q POC BCB（1）求证：AE = BE.（2）若⊙O的半径为5，AD= 4，求AE的长.初中-数学-打印版。

（5）（4）A24.1.4圆周角导学案（1）学习目标：1.了解圆周角的概念．理解圆周角的定理．理解圆周角定理的推论.（重点）2.熟练掌握圆周角的定理及其推理的灵活运用．（难点） 自主学习：阅读教材85至86页 1.定义：顶点在 ，并且两边都和圆 的角叫做圆周角.（完成书后练习第1题） 2. ① 如图，AB 为⊙O 的直径，∠BOC 、∠BAC 分别是所对的圆心角、圆周角，利用以前所学知识求出图（1），（2），（3）中∠BAC 的度数分别为 ．通过计算发现：∠BAC ＝ ∠BOC ， 即， 。

② 观察图（4）和（5）中的圆周角和圆心角，它们与图（1）（2）（3）有什么不同？还能得到与①相同的结论吗？你是怎么得到的？③ 圆周角定理的证明运用了什么数学思想？3.如图（6），在⊙O 中，所对的圆心角为 ，所对的圆周角是 ，你能得到什么结论？合作探究探究1 教材88页练习3 探究2 教材88页练习2 典型题例1.如图（7），点A 、B 、C 、D 在⊙O 上，点A 与点D 在点B 、C 所在直线的同侧，∠BAC=350①∠BDC=_______°,理由是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿． ②∠BOC=_______°,理由是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿． 2.如图（8），点A ，B ，C 在⊙O 上， 若∠BAC=60°，则∠BOC=____°；若∠AOB=90°，则∠ACB=____°. 3.如图（9），点A 、B 、C 、D 在⊙O 上，∠ADC=∠BDC=60°.判断△ABC 的形状，并说明理由.4.如图（10），⊙O 的直径AB=8cm,∠CBD=30°，求弦DC 的长.BC （1） （2） （3）BC （6）（7）（8）(9)（10）B（13）圆周角（1）限时训练1.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( ) A.30° B.30°或150° C.60° D.60°或120°2.如图,A 、B 、C 三点都在⊙O 上,点D 是AB 延长线上一点,∠AOC=140°, ∠CBD 的度数是( ) A.40° B.50° C.70° D.110°3.如图,已知圆心角∠BOC=100°,则圆周角∠BAC 的度数是( ) A.50° B.100° C.130° D.200°4.如图，A 、B 、C 、D 四点在同一个圆上，四边形ABCD 的对角线把四个内角分成的八个角中，相等的角有( ) A.2对 B.3对 C.4对 D.5对5.如图,D 是弧AC 的中点,则图中与∠ABD 相等的角的个数是( ) A.4个 B.3个 C.2个 D.1个6.如图,∠AOB=100°,则∠A+∠B 等于( ) A.100° B.80° C.50° D.40°7.如图⊙O 中弧AB 的度数为60°，AC 是⊙O 的直径，那么∠BOC 等于 ( ) A ．150° B ．130° C ．120° D ．60°8.如图,等边三角形ABC 的三个顶点都在⊙O 上,D 是弧AC 上任一点(不与A 、C 重合),则∠ADC 的度数是________.9.如图,四边形ABCD 的四个顶点都在⊙O 上,且AD ∥BC,对角线AC 与BD 相交于点E,那么图中有_________对全等三角形.10.已知,如图,∠BAC 的邻补角∠BAD=100°,则∠BOC=_____度. 11.如图,A 、B 、C 为⊙O 上三点，若∠OAB=46°,则∠ACB=_____度.12.如图,AB 是半圆O 的直径,AC=AD,OC=2,∠CAB= 30 °,则点O 到CD 的距离OE= . 13.如图（13）,A 、B 、C 、D 四点都在⊙O 上，AD 是⊙O 的直径，且AD=6cm ，若∠ABC=∠CAD,求弦AC 的长.第2题第3题 第4题 第5题 第7题 第6题 第9题 第10题 CD 第11题 第12题24.1.4圆周角导学案（2）学习目标：1．掌握直径（或半圆）所对的圆周角是直角及90°的圆周角所对的弦是直径。

圆周角（1）导学案班级：_ ______ __ 姓名： __________【学习目标】1、知道圆周角的概念，会证明圆周角定理。

2、经历探索圆周角的有关性质的过程，体会分类、转化等数学思想方法。

3、会运用圆周角定理解决简单问题。

【学习重点】圆周角概念及圆周角定理.【学习难点】圆周角定理的推导过程。

【学习过程】一、知识回顾:☆顶点在圆心的角叫做 ,如图(1)中∠AOB是二、课堂探究：知识一：圆周角的概念（阅读教材P85内容，回答下列问题）1.圆周角的定义：图2中CD所对的圆周角的有_______________________________2.圆周角的两个特征：（1）（2）知识二：圆周角定理（阅读教材P85-86内容，回答下列问题）思考与探索：1、如图(3)，∠BAC是圆周角，请作出BC所对的圆心角∠BOC∠BAC和∠BOC的度数，发现它们之间有什么关系？2、再在⊙O上任取一条弧，作出这条弧所对的圆周角和圆心角，测量它们的度数，是否得出同样的结论？你能发现什么规律吗？3、如何证明上面的结论？︵︵分析：在⊙O上任取BC，画出它所对的圆周角∠BAC，这样的圆周角有多少个？按圆心O与圆周角的位置关系又可以分成几种情况?(4) (5) (6)结合上图（4）（5）（6）分别完成证明过程。

4、圆周角定理：一条弧所对的________等于这条弧所对的圆心角的__________。

几何语言表示：三、随堂练习︵1、求⊙O 中角x 的度数：(1)(2)2、 如图，在直径为AB 的半圆中，O 为圆心，C 、D 为半圆上的两点，∠COD=500，则∠CAD=_______ 3、如右图，AB 、AC 、BC 都是⊙O 的弦，若∠CAB ＝∠CBA ，则∠COB =∠ ,AC=_____ ，AC=____4、如图，OA,OB,OC 都是⊙O 的半径，∠AOB=2∠BOC.求证：∠ACB=2∠BAC.四、能力提升1、已知⊙O 中弦AB 的长度等于半径，求弦AB 所对的圆心角和圆周角的度数︵2、如图，点A、B、C、D在⊙O上，∠ADC=∠BDC=60°.判断△ABC的形状，并说明理由.【课堂小结】1.圆周角定义： ,并且的角叫圆周角.2.圆周角定理：一条弧所对的，等于所对的一半。

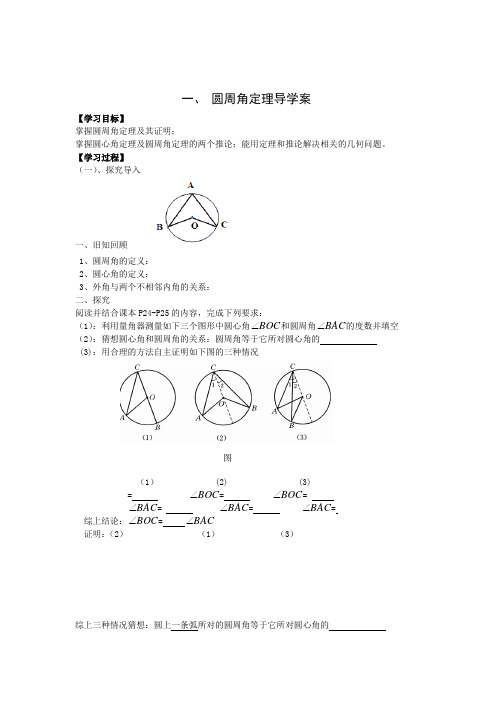
一、 圆周角定理导学案【学习目标】掌握圆周角定理及其证明；掌握圆心角定理及圆周角定理的两个推论；能用定理和推论解决相关的几何问题。

【学习过程】 （一）、探究导入一、旧知回顾1、圆周角的定义：2、圆心角的定义：3、外角与两个不相邻内角的关系： 二、探究阅读并结合课本P24-P25的内容，完成下列要求： （1）：利用量角器测量如下三个图形中圆心角BOC ∠和圆周角BAC ∠的度数并填空 （2）：猜想圆心角和圆周角的关系：圆周角等于它所对圆心角的 (3)：用合理的方法自主证明如下图的三种情况（1） (2) (3)= BOC ∠= BOC ∠=BAC ∠= BAC ∠= BAC ∠= 综上结论：BOC ∠= BAC ∠ 证明：（2） （1） （3）综上三种情况猜想：圆上一条弧所对的圆周角等于它所对圆心角的图（二）、新课传授一、1.圆周角定理：圆上一条弧所对的圆周角等于它所对圆心角的2.练习：1、如图1，在⊙O中，∠ABC=50°，则∠AOC等于（）A、50°B、80°C、90°D、100°图1 图2练习： 2、如图2，△ABC的顶点A、B、C都在⊙O上，∠C＝30 °AB＝2，则⊙O 的半径是。

二、1、思考（1）如图3.弧AC所对的圆周角∠ AEC ∠ ABC ∠ ADC的大小有什么关系？图3 图4 图5 （2）如图4.在同圆或等圆中，如果两个圆周角相等，它们所对弧一定相等吗？为什么？（3）如图5.问题1：如图，AB是⊙O的直径，请问：∠C1、∠C2、∠C3的度数是问题2：若∠C1、∠C2、∠C3是直角，那么∠AOB是。

2、圆心角定理：圆心角的度数它所对弧的度数。

3、圆周角定理的推论推论①：同弧或等弧所对的圆周角；同圆或等圆中，相等的圆周角所对的弧。

推论②：半圆（或直径）所对的圆周角是；90的圆周角所对的弦是4.判断正误（1）同弧或等弧所对的圆周角相等（）（2）相等的圆周角所对的弧相等（）（3）90°角所对的弦是直径（）（4）直径所对的角等于90°（）（5）长等于半径的弦所对的圆周角等于30°（）1．如图一，在⊙O 中，∠BAC ＝60°，则∠BDC ＝( )A ．30° B.45° C ．60° D.75°图一三、学以致用例1：如图，ΔABC 中，AB=AC ， ΔABC 外接圆⊙O 的弦AE 交BC 于点D ，求证：练习：1图2－1－ 5 2－1－102．如图2－1－10，A 、B 、C 是⊙O 的圆周上三点，若∠BOC ＝3∠BOA ，则∠CAB 是∠ACB 的________倍．AE AD AB ⨯=2 如图2－1－5，已知等腰三角形ABC 中，以腰AC 为直径作半圆交AB 于点E ，交BC 于点F ，若∠BAC ＝50°，则EF ︵的度数为( ) A ．25° B.50° C ．100°D.120°BCA练习.2、如图所示，OA OA 是⊙O 的半径，以OA 为直径的⊙C 与⊙O 的弦 AB AB 相交于D ，AO 的延长线交⊙O 于E 求证：D D 是AB 的中点.2、如图，BC 为⊙O 的直径，BC AD ⊥,垂足为D ，AB =AF ,BF 和AD 相交于E ，求证：BE AE =三、师生互动1.如图所示，已知AD 是ABC ∆的高，AE 是ABC ∆的外接圆直径 求证：（1）AD AE AC AB ⋅=⋅ (2) DAC BAE ∠=∠______2tan 307.(12==∠=⊥θθ则设且于在半圆上的直径是半圆年深圳一模，COD BD ，AD D AB ，CD C ，O ）ABAPAC2.如图所示，AB 与CD 相交于圆内一点P .求证：AD 弧的度数与BC 弧的度数和的一半等于APD ∠的度数.（你能用两种方法吗？）变式：如图，圆O 的两条弦的延长线相交于点P .求证：BC 弧的度数与AD 弧的度数差的一半等于APD ∠的度数.【课时作业】（大小题均写解题过程）1.下列说法中：①直径相等的两个圆是等圆；②长度相同的两条弧是等弧；③圆中最长的弦是过圆心的弦；④一条弦把圆分成两条弧，这两条弧不可能是等弧，正确的序号是 .2.如图所示，已知A 、B 、C 、D 、E 均在⊙O 上，且AC 为⊙O 的直径， 则C B A ∠+∠+∠= .3.在半径为cm 7的圆内有长为cm 37的弦，则此弦所对圆周角的度数 为 .4.已知：如图，AB 是弦O Θ的一条弦，ACB ∠的平分线交AB 于点E ，交⊙O 于点D .D求证：CBDCCE AC =.5.如图，圆内接ABC ∆中，AC AB =,D 是BC 边上的一点，E 是直线AD 和ABC ∆外接圆的交点，(1)求证：AE AD AB ⋅=2；（2）当D 为BC 延长线上的一点时，第（1）题的结论还成立吗？若成立，请证明；若不成立，请说明理由。

课题：24.1.4 圆周角【学习目标】1.理解圆周角的定义,掌握圆周角定理.2.初步运用圆周角定理解决相关问题.3.掌握圆内接四边形的概念及其性质,并能灵活运用.【学习重难点】圆周角与圆心角的关系，圆周角的性质和直径所对圆周角的特征；圆内接四边形的概念及其性质.运用数学分类思想证明圆周角的定理.【课前预习案】什么叫圆心角?在图1中画出所对的圆心角,能画几个?圆周角定义：1.定义:________________________________________叫圆周角.辨析:图中的角是圆周角的是_____________.2.在图1中画出弧所对的圆周角.能画几个?【课中探究案】探究1:1.根据圆周角与圆心的位置关系可将圆周角分为几类?在下图中画出所对的圆周角.2.量出所对的圆周角和∠AOB的度数你会发现: .3.尝试证明你的发现.归纳:圆周角定理: .在图中,由圆周角定理可知:∠ADB ∠ACB= .思考:在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等吗?为什么?探究2:在图中画出直径AB所对的圆周角,你有什么发现?归纳:圆周角定理的推论:探究3：如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做,这个圆叫做这个 .问题1:如图,四边形ABCD叫做☉O的内接四边形,而☉O叫做四边形ABCD的外接圆,猜想:∠A与∠C,∠B与∠D之间的关系为 . 由此得出圆内接四边形的性质: .典例精析1.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?2.四边形ABCD是☉O的内接四边形,∠A与∠C是一对对角,且∠A=110°,∠B=80°,则∠C=,∠D=.3.☉O的内接四边形ABCD中,∠A,∠C是一对对角,∠A∶∠B∶∠C=1∶2∶3,则∠D=.【课末达标案】1．如图1,点A，B，C在⊙O上，∠A=40度，∠C=20度，则∠B= 度．2．如图2，AB是半圆的直径，∠BAC=20°，D是的中点，则∠DAC的度数是．3．如图3，△ABC内接于⊙O，若⊙O的半径为4，∠A=60°，则BC的长为．图1 图2 图34．如图4，AB、AC是⊙O的弦，OE⊥AB、OF⊥AC，垂足分别为E、F．如果∠EOF=100°，∠C=60°，那么∠FEA= ．5．如图5，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AE．若∠D=72°，则∠BAE= °．图5图 46.如图，AB是⊙O的直径，C、D两点在⊙O上，若∠C=45°.（1）求∠ABD的度数；（2）若∠CDB=30°，BC=3，求⊙O的半径．【课后拓展案】基础达标：1．如图1，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（）A．75° B．70° C．65° D．35°图1 图2 图3 图4 图5 图62．如图2，⊙O是△ABC的外接圆，已知∠ABO=50°，则∠ACB的大小为（）A．40° B．30° C．45° D．50°3．如图3，⊙O中，弦BC与半径OA相交于点D，连接AB，OC．若∠A=60°，∠ADC=85°，则∠C的度数是（）A．25° B．27.5°C．30° D．35°4.如图4，AB是半圆的直径，O为圆心，C是半圆上的点，D是上的点，若∠BOC=40°，则∠D的度数为（） A．100° B．110°C．120°D．130°5.如图5，A，B，C为⊙O上三点，∠AOB=110°，则∠ACB等于（）A.55°B.110°C.125°D.140°6.如图6，点A、B、C、D都在⊙O上，且四边形OABC是平行四边形，则∠D的度数为（）A.45°B.60°C.75°D.不能确定应用提高：7．已知在⊙O 上依次有A、B、C三点，∠AOB=100°，则∠ACB的度数是（）A．50°B．130°C．50°或l30°D．100°8．如图，△ABC内接于⊙O，若∠BAC=30°，BC=3，则⊙O的半径为．9．如图，在△ABC中，AB=AC=13，BC=10，以AC为直径画⊙O交BC于点D，交AB于点E，连接CE．（1）求证：BD=CD；（2）求CE的长．思维拓展：10．如图，△ABC内接于⊙O，AD交BC于点D，点P是的中点，求证：AP平分∠OAD．11如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．（1）若∠B=70°，求∠CAD的度数；（2）若AB=4，AC=3，求DE的长．。

最新人教版九年级数学上册《圆》全单元导学案最新人教版九年级数学上册《圆》导学案研究目标：1.理解圆的概念；2.掌握解答基本的圆题型。

研究重点：1.圆的概念。

研究难点：1.解答基本的圆题型。

教学流程：导课】前段时间我们研究了图形的旋转，图形的旋转创造了生活中的许多美好的事物！我们知道：一条线段至少旋转360°能和自身重合；一个等边三角形至少旋转120°能和自身重合；一个正方形至少旋转90°能和自身重合；思考：圆绕其圆心旋转任何度数都能和自身重合吗？圆是生活中常见的图形，许多物体都给我们以圆的形象，比如：摩天轮、硬币、呼啦圈、方向盘、车轮、月亮、太阳等等。

那么，圆的基本要素是圆心和半径，其中圆心确定了圆的位置，半径确定了圆的大小。

当点A绕点B旋转一周时，点A的运动轨迹其实就是一个圆，其中点B是圆心。

阅读质疑自主探究】自学要求：阅读课本P78-P79圆的定义：1.在同一平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆。

2.到定点O的距离等于定长的所有的点组成的图形。

（含义也是判断点在圆上的方法）表示方法：“⊙O”读作“圆O”。

构成元素：1.圆心、半径（直径）。

2.弦：连接圆上任意两点的线段叫做弦。

直径是经过圆心的弦，是圆中最长的弦。

3.优弧：大于半圆的弧；半圆弧：直径分成的两条弧；劣弧：小于半圆的弧。

如图：优弧ABC记作，半圆弧AB记作，劣弧AC记作。

4.同心圆：圆心相同，半径不同的两圆。

5.等圆：能够重合的两个圆。

6.等弧：在同圆或等圆中，能够互相重合的弧叫做等弧。

多元互动合作探究】1.如图，在圆O中，AC、BD为直径，求证：XXX。

2.如图，OA、OB为圆O的半径，C、D为OA、OB上两点，且AC=BD。

求证：AD=BC。

训练检测目标探究】1.下列说法正确的是：①直径是弦；②弦是直径；③半径是弦；④半圆是弧，但弧不一定是半圆；⑤半径相等的两个半圆是等弧；⑥长度相等的两条弧是等弧；⑦等弧的长度相等。

24.1.1 圆导学案1 理解并掌握圆的有关概念.2 能灵活运用圆的有关概念解决相关的实际问题.3 通过解决圆的有关问题，发展学生有条理的思考能力及解决实际问题的能力.★知识点1：圆的概念：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆.，一般用r表示.以点O为圆心的圆，记作“★O”，读作“圆O”.圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形.★知识点2：弦的概念：连接圆上任意两点的线段（如图AC）叫做弦.经过圆心的弦（如图中的AB）叫做直径.★知识点3：弧、半圆、优弧、劣弧的概念：̂，读作“圆弧AB”或“弧AB”.圆上任意两点间的部分叫做圆弧，简称弧．以A、B为端点的弧记作AB圆的任意一条直径的两个端点把圆分成的两条弧，每一条弧都叫做半圆.̂）叫做劣弧小于半圆的弧（如图中的AB̂）叫做优弧.大于半圆的弧（用三个字母表示，如图中的ACB★知识点4：同心圆、等圆的概念：圆心相同，半径不相等的两个圆叫做同心圆.能够互相重合的两个圆叫做等圆.★知识点5：等弧的概念：在同圆或等圆中，能够互相重合的弧叫做等弧.一、圆的概念：在一个________内，线段OA绕它________的一个端点O________一周，另一个端点A________________叫做圆.其中，________________叫做圆心. _______________________为圆心的圆，记作“________________”，读作“________________”.圆心为O、半径为r的圆可以看成是________________________________组成的图形.二、弦的概念：连接圆上________________________________________叫做直径.三、弧、半圆、优弧、劣弧的概念：̂，读作“圆弧AB”或“弧AB”.圆上______________叫做圆弧，简称弧．以A、B为端点的弧记作AB圆的任意一条直径的两个端点把圆________________，每一条弧都叫做半圆.̂）叫做劣弧________半圆的弧（如图中的AB̂）叫做优弧.________半圆的弧（用三个字母表示，如图中的ACB四、同心圆、等圆的概念：____________相同，__________不相等的两个圆叫做同心圆.能够___________________的两个圆叫做等圆.五、等弧的概念：在______________中，能够____________的弧叫做等弧.引入新课【提问】小学阶段我们学习了圆的哪些性质？新知探究观察这些图片，你认识图片中的图形吗？【提问】用什么办法可以画出一个圆？圆的概念（动态）：[问题一]圆上各点到定点（圆心O）的距离有什么规律？[问题二]到定点的距离等于定长的点又有什么特点？圆的概念（静态）：【问题三】以定长为半径能画几个圆，以定点为圆心能画几个圆？【问题四】确定一个圆的要素是？【问题五】观察车轮形状，你发现了什么？【问题六】你知道车轮均为圆形的原因吗？典例分析例1 已知：矩形ABCD的对角线AC、BD相交于点O.求证：A、B、C、D四个点在以点O为圆心的同一个圆上.【针对训练】1．下列条件中，能确定一个圆的是（）A．以点O为圆心B．以10cm长为半径C．以点A为圆心，4cm长为半径D．经过已知点M2．画圆时，圆规两脚间可叉开的距离是圆的（）A．直径B．半径C．周长D．面积新知探究【问题】通过阅读课本，你能说出弦的概念吗？【提问】直径和弦是什么关系呢？【课堂练习】1 判断下列说法的正误：1)弦是直径（）2)直径是弦（）3)半径是弦（）4)直径是圆中最长的弦（）5)过圆心的线段是直径（）6)过圆心的直线是直径（）2 如图，点B、O、C和点A、O、D分别在同一条直线上，则图中有（）条弦．3. 如图,点A、B、C、D在★O上,试在图中画出以这4点中的2点为端点的弦,这样的弦共有多少条？【问题】通过阅读课本，你能说出弧、半圆、优弧、劣弧的概念吗？【提问】弧、半圆、优弧、劣弧是什么关系呢？【课堂练习】1 判断下列说法的正误：(1)半圆是弧（）(2)圆的任意一条弦把圆分成优弧和劣弧两部分（）(3)大于半圆的弧叫做劣弧（）2.如图，请正确的方式表示出以点A为端点的优弧及劣弧.3．如图,圆中以A为一个端点的优弧有_____条,劣弧有_____条.【问题】通过阅读课本，你能说出同心圆、等圆的概念吗？【问题】通过阅读课本，你能说出等弧的概念吗？̂和CD̂的拉直长度都是10cm，平移并调整小圆的位置，是否能使这两条弧完全重合？【提问】如图，如果AB1.如图,一根3m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.2.如图,一根6m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.3.一些学生正在做投圈游戏，他们呈“一”字排开．这样的队形对每一人都公平吗？你认为他们应当排成什么1．（2021·江苏徐州·统考中考真题）如图，一枚圆形古钱币的中间是一个正方形孔，已知圆的直径与正方形的对角线之比为3：1，则圆的面积约为正方形面积的（）A．27倍B．14倍C．9倍D．3倍【参考答案】观察这些图片，你认识图片中的图形吗？图片中的图形是一个圆【提问】用什么办法可以画出一个圆？圆的概念（动态）：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆.其中，固定的端点O叫做圆心.线段OA叫做半径,一般用r表示.以点O为圆心的圆，记作“★O”，[问题一]圆上各点到定点（圆心O ）的距离有什么规律？圆上各点到定点（圆心O ）的距离都等于定长（半径r ）[问题二]到定点的距离等于定长的点又有什么特点？到定点的距离等于定长的点都在同一个圆上.圆的概念（静态）：圆心为O 、半径为r 的圆可以看成是所有到定点O 的距离等于定长r 的点组成的图形.【问题三】以定长为半径能画几个圆，以定点为圆心能画几个圆？以定长为半径能画无数个圆，以定点为圆心能画无数个圆.【问题四】确定一个圆的要素是？一是圆心，圆心确定其位置；二是半径，半径确定其大小．【问题五】观察车轮形状，你发现了什么？车轮的形状均为圆形【问题六】你知道车轮均为圆形的原因吗？把车轮做成圆形，车轮上各点到车轮中心（圆心）的距离都等于车轮的半径，当车轮在平面上滚动时，车轮中心与平面的距离保持不变，因此，当车辆在平坦的路上行驶时，坐车的人会感觉到非常平稳，假如车轮变了形，不成圆形了，到轴的距离不相等了，车就不会再平稳.典例分析例1 已知：矩形ABCD 的对角线AC 、BD 相交于点O.求证：A 、B 、C 、D 四个点在以点O 为圆心的同一个圆上.证明：★四边形ABCD 为矩形，★AO=OC=12AC ，OB=OD= 12 BD ，AC=BD.★OA=OC=OB=OD.★A、B、C、D四个点在以点O为圆心，OA为半径的圆上.【针对训练】1．下列条件中，能确定一个圆的是（C）A．以点O为圆心B．以10cm长为半径C．以点A为圆心，4cm长为半径D．经过已知点M2．画圆时，圆规两脚间可叉开的距离是圆的（B）A．直径B．半径C．周长D．面积新知探究【问题】通过阅读课本，你能说出弦的概念吗？连接圆上任意两点的线段（如图AC）叫做弦.经过圆心的弦（如图中的AB）叫做直径.【提问】直径和弦是什么关系呢？1.弦和直径都是线段.2.凡直径都是弦，是圆中最长的弦，但弦不一定是直径.【课堂练习】1 判断下列说法的正误：1)弦是直径（×）2)直径是弦（√）3)半径是弦（×）4)直径是圆中最长的弦（√）5)过圆心的线段是直径（×）6)过圆心的直线是直径（×）2 如图，点B、O、C和点A、O、D分别在同一条直线上，则图中有（B）条弦．3. 如图,点A、B、C、D在★O上,试在图中画出以这4点中的2点为端点的弦,这样的弦共有多少条？6条【问题】通过阅读课本，你能说出弧、半圆、优弧、劣弧的概念吗？【提问】弧、半圆、优弧、劣弧是什么关系呢？̂，读作圆上任意两点间的部分叫做圆弧，简称弧．以A、B为端点的弧记作AB“圆弧AB”或“弧AB”.圆的任意一条直径的两个端点把圆分成的两条弧，每一条弧都叫做半圆.̂）叫做劣弧小于半圆的弧（如图中的AB̂）叫做优弧.大于半圆的弧（用三个字母表示，如图中的ACB【课堂练习】1 判断下列说法的正误：(1)半圆是弧（√）(2)圆的任意一条弦把圆分成优弧和劣弧两部分（×）(3)大于半圆的弧叫做劣弧（×）2.如图，请正确的方式表示出以点A为端点的优弧及劣弧.3．如图,圆中以A为一个端点的优弧有__3___条,劣弧有__3___条.【问题】通过阅读课本，你能说出同心圆、等圆的概念吗？圆心相同，半径不相等的两个圆叫做同心圆.能够互相重合的两个圆叫做等圆.【问题】通过阅读课本，你能说出等弧的概念吗？在同圆或等圆中，能够互相重合的弧叫做等弧̂和CD̂的拉直长度都是10cm，平移并调整小圆的位置，是否能使这两条弧完全重合？【提问】如图，如果AB这两条弧不可能完全重合,实际上这两条弧弯曲程度不同.1.如图,一根3m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.2.如图,一根6m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.3.一些学生正在做投圈游戏，他们呈“一”字排开．这样的队形对每一人都公平吗？你认为他们应当排成什么样的队形？不公平，应该站成圆形.1．（2021·江苏徐州·统考中考真题）如图，一枚圆形古钱币的中间是一个正方形孔，已知圆的直径与正方形的对角线之比为3：1，则圆的面积约为正方形面积的（B）A．27倍B．14倍C．9倍D．3倍。

圆周角导学案（课时2）知识点回顾：1.顶点在，且两边与圆 的角叫圆周角。

2．在同圆或__________中，同弧或_______所对的圆周角________，都等于这条弧所对的_________的一半．3．半圆(或________)所对的圆周角是_________；90°的圆周角所对的弦是__________． 练习：1.下列图形中的角是圆周角的是( )2.如图A ，B ，C 是⊙O 上的三点，且∠ABC ＝70°，则∠AOC 的度数是( )A ．35°B ．140°C ．70°D ．70°或140°3.如图，在⊙O 中，直径CD 垂直于弦AB ，若∠C ＝25°，则∠ABO 的度数是( )A ．25°B ．30°C ．40°D ．50°4.如图，⊙O 是△ABC 的外接圆，∠C ＝30°，AB ＝2 cm ，则⊙O 的半径为______cm.5.△ABC 为⊙O 的内接三角形，若∠AOC ＝160°，∠ABC 的度数是( )A ．80°B ．160°C ．100°D ．80°或100°新知讲解：圆内接多边形概念如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做______________，这个圆叫做_______________；圆内接多边形性质圆内接四边形对角_________．练习1：书上88页练习5例1：求证：圆内接平行四边形是矩形。

第2题图 第3题图 第4题图例2：如图，四边形ABCD 内接于⊙O ，∠B ＝50°，∠ACD ＝25°，∠BAD ＝65°. 求证：(1)AD ＝CD ；(2)AB 是⊙O 的直径．练习2：如图，点A ，B ，C 在⊙O 上，∠AOC ＝60°，则∠ABC 的度数是____________．练习3：如图，点A ，B ，C ，D 在⊙O 上，O 点在∠D 的内部，四边形OABC 为平行四边形，则∠OAD ＋∠OCD ＝_________.练习4：如图，以原点O 为圆心的圆交x 轴于A ，B 两点，交y 轴的正半轴于点C ，D 为第一象限内⊙O 上的一点，若∠DAB ＝20°，则∠OCD ＝__________．例3：已知，如图所示，BC 为半圆O 的直径，弧AB=弧AF ，AC 与BF 交于点M（1）若∠FBC=∂，求∠ACB （用∂表示）（2）过A 作AD ⊥BC 于D ，交BF 于E 求证：BE=EM练习2图 例2图练习3图练习4图 C EM B A F O。

一、自主预习1．回顾圆心角的概念以及在同圆和等圆中圆心角、弦、弧之间的关系。

2、自学课本第85页的内容.圆周角的概念：顶点在_______，并且两边____________________的角叫做圆周角。

强调条件：①_______________，②_______________。

练习：判断下列各图中的角是否是圆周角？并说明理由．3、自学课本第85页与86页的内容.圆周角定理：一条弧所对的圆周角等于这条弧所对的圆心角的______ 几何语言：推论1：同弧或等弧所对的圆周角相等几何语言：推论2：半圆（或直径）所对的圆周角是_______，反之，90º的圆周角所对的弦是____________ 几何语言：二、合作探究如图在☉O 中,直径AB 与弦CD 相交于点P,∠CAB=40°,∠APD=65°(1)求∠B 的度数;(2)已知圆心O 到BD 的距离为3,求AD 的长.三、展示交流1、如图，⊙O 直径AB 为10cm ，弦AC 为6cm ，∠ACB 的平分线交⊙O 于D ，求BC ，AD ，BD 的长科目数学班级：学生姓名课题24.1.4圆周角课 型新授课时 1 主备教师备课组长学习目标： 1、理解圆周角的概念。

2、探索圆周角与同弧所对的圆心角的关系，并能应用圆周角定理及推论进行简单的论证和计算。

学习重点圆周角概念和圆周角定理 学习难点理解圆周角定理的证明AC B OC ABPA C BOD E2、如果一个多边形 ，这个多边形叫做圆内接多边形，这个圆叫做 。

探究圆内接四边形的四个内角之间有什么关系？四、随堂检测 班级： 姓名：1．如图，在⊙O 中，∠ABC=50°， 则∠AOC 等于（ ） A 、50° B 、80° C 、90° D 、100°2．如图，△ABC 是等边三角形， 动点P 在圆周的劣弧AB 上，且不与A 、B 重合，则∠BPC 等于（ ）A 、30°B 、60°C 、90°D 、45°3．如图，∠A=50°， ∠ACB=60 °BD 是⊙O 的直径，则∠AEB 等于（ ）A 、70°B 、100°C 、90°D 、120°4．如图，△ABC 的顶点A 、B 、C 都在⊙O 上，∠C ＝30 °， AB ＝2，则⊙O 的半径是 。