建筑基础沉降计算例题

问题：理正勘察软件地基沉降计算无法考虑孔口高程与建筑设计±0.00不相等的情况沉降计算主要考虑地基中的附加应力P0，只要保证软件计算的P0与实际情况的P0相等即可。

实际情况地基附加应力如下：P0=（F+G）/A-γh=（F+γG dA）/A-γh=F/A+γG d-γh式中P0基底附加应力F 上部结构传至基础顶的压力G 基础底至建筑设计±0.00之间的基础和回填土的重力，G=γG dAA 基底面积γ基础底至孔口高程（自然地面）之间的土层加权平均重度值γG基础底至建筑设计±0.00之间基础和回填土的加权平均重度值d 基础底至建筑设计±0.00之间的距离h 基础底至孔口高程（自然地面）的距离软件中计算P0方法为：P0’=（F’+G）/A-γ’d=（F’+γG dA）/A-γ’d = F’/A+γG d-γ’d式中P0’软件计算的基底附加应力F’输入理正里的数值（见下图）γ’基础底至建筑设计±0.00之间的土层加权平均值（理正勘察软件中无法输入h，默认h=d）要使计算正确，只需令实际的基底附加应力与软件计算的附加应力相等即可，即令P0= P0’即P0=F/A+γG d-γh= P0’= F’/A+γG d-γ’dF/A -γh= F’/A -γ’dF’/A= F/A –γh+γ’d假设γ=γ’，其实两个数有一个微小的差值，忽略不计得到F’/A= F/A +γ（d-h）F’ = F +γ（d-h）A变形得F’ =（P准永久值-γG d）A+γ（d-h）AP准永久值结构专业在基础图中给出的基底准永久组合基底压力值上式中γ（d-h）项正是考虑了孔口高程与建筑设计±0.00不相等而引起的基底自重压力不一样，从而考虑附加应力不一样的偏差。

注意的是，d与h的相对大小关系不确定。

若再令γG=γ，则可进一步简化为F’ =（P准永久值-γh）A结论：理正勘察软件中输入“基础顶轴力准永久值（kN）”应采用F’ =（P准永久值-γG d）A+γ（d-h）A或F’ =（P准永久值-γh）A计算出的结果。

沉降量计算方法①用坐标纸按比例绘制土层分布剖面图和基础剖面图，如图所示。

分层总和法计算地基沉降②计算地基土的自重应力σｃ，土层变化处为计算点。

计算结果按照力的比例尺（如１ｃｍ代表１００ｋＰａ）绘于基础中心线左侧，注意自重应力分布曲线的横坐标只表示该点的自重应力值，应力的方向都是竖直方向。

③计算基础底面的接触压力。

④计算基础底面的附加应力。

⑤沉降计算分层。

为使地基沉降计算比较精确，除按０．４b 和１～２ｍ分层以外，还需考虑下列因素：ａ．地质剖面图中，不同的土层，因压缩性不同应为分层面；ｂ．地下水位应为分层面；ｃ．基础底面附近的附加应力数值大且曲线的曲率大，分层厚度应小些，使各计算分层的附加应力分布曲线以直线代替计算时误差较小。

⑥计算地基中的附加应力分布。

按分层情况将附加应力数值按比例尺绘于基础中心线的右侧。

例如，深度z处，M点的竖向附加应力σz值，以线段Mm表示。

各计算点的附加应力连成一条曲线KmK′，表示基础中心点O以下附加应力随深度的变化。

⑦确定地基受压层深度zn。

由上图中自重应力和附加应力分布两条曲线，可以找到某一深度处附加应力σz为自重应力σｃz的２０％，此深度称为地基受压层深度zn。

４）分层总和法特点分层总和法计算沉降的优点是概念比较明确，计算过程及变形指标的选取比较简便，易于理解掌握，适用于不同地基土层的情况。

但是采用上述方法进行建筑物地基沉降计算，并与大量建筑物的沉降观测值比较，发现具有下列规律：①对于中等地基，计算沉降量与实测沉降量相近，即s计≈s 实；②对于软弱地基，计算沉降量远小于实测沉降量，即s计＜s 实；③对于坚实地基，计算沉降量远大于实测沉降量，即s计＞s 实。

地基沉降量计算值与实测值不一致的原因主要有以下３个方面：①分层总和法计算所作的几点假定，与实际情况不完全相符；②土的压缩性指标试样的代表性、取原状土的技术及实验的准确度都存在问题；③在地基沉降计算中，没有考虑地基、基础与上部结构的共同作用。

1．某正常固结土层厚2.0m ，其下为不可压缩层，平均自重应力100cz a p kP =；压缩试验数据见表，建筑物平均附加应力0200a p kP =，求该土层最终沉降量。

【解】土层厚度为2.0m ，其下为不可压缩层，当土层厚度H 小于基础宽度b 的1/2时，由于基础底面和不可压缩层顶面的摩阻力对土层的限制作用，土层压缩时只出现很少的侧向变形，因而认为它和固结仪中土样的受力和变形很相似，其沉降量可用下式计算：1211e e s H e -=+ 式中，H ——土层厚度；1e ——土层顶、底处自重应力平均值c σ，即原始压应力1c p σ=，从e p-曲线上得到的孔隙比e ；2e ——土层顶、底处自重应力平均值c σ与附加应力平均值z σ之和2c z p σσ=+，从e p -曲线上得到的孔隙比e ；1100c a p kP σ==时，10.828e =；2100200300c z a p kP σσ=+=+=时，20.710e = 1210.8280.7102000129.1110.828e e s H mm e --==⨯=++2．超固结黏土层厚度为4.0m ，前期固结压力400c a p kP =，压缩指数0.3c C =，再压缩曲线上回弹指数0.1e C =，平均自重压力200cz a p kP =，天然孔隙比00.8e =，建筑物平均附加应力在该土层中为0300a p kP =，求该土层最终沉降量。

【解】超固结土的沉降计算公式为：当c cz p p p ∆>-时（300400200200a c cz a p kP p p kP ∆=>-=-=）时，10lg lg 1ni ci li i cn ei cii ili ci H p p p s C C e p p =⎡⎤⎛⎫⎛⎫+∆=+⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎣⎦∑式中，i H ——第i 层土的厚度；0i e ——第i 层土的初始孔隙比；ei C 、ci C ——第i 层土的回弹指数和压缩指数； ci p ——第i 层土的先期固结压力；li p ——第i 层土自重应力平均值，()12c i li ci p σσ-⎡⎤=+⎣⎦；i p ∆——第i 层土附加应力平均值，有效应力增量()12z i i zi p σσ-⎡⎤∆=+⎣⎦。

YJK 基础沉降计算的使用要点及案例1 沉降计算的有关规范规定（1）沉降验算的规范规定问题1：哪些需要验算沉降《建筑地基基础设计规范》第 3.0.2 条规定“设计等级为甲级、乙级的建筑物，均应按地基变形设计”，并规定六类情形下的丙类建筑物，“仍应作变形验算”。

是否需要进行基础沉降验算，软件不自动判断，由用户根据上述规范条件判断。

问题2：建筑物沉降验算满足要求的判断标准所谓地基变形验算，即要求地基的变形计算值在允许的范围内：∆≤[∆] （1）式中：[∆]—地基的允许变形值，按《建筑地基基础设计规范》5.3.4 条取值。

《地基规范》表5.3.4 给出了建筑物的地基变形允许值，控制指标包括沉降量、沉降差、倾斜、局部倾斜。

《桩基规范》表5.5.4 给出了建筑桩基沉降变形允许值，控制指标包括沉降量、沉降差、倾斜、局部倾斜。

YJK 基础软件统一给出所有基础的沉降验算结果，见下图：沉降量应查看沉降等值线图，软件以等值线加数值的方式给出所有基础的沉降量计算结果。

注意两点：1）桩沉降是包括了土沉降及桩身压缩的总值；2）考虑土回弹再压缩情况（一般是基础埋深超过5 米情况），沉降总值要查看【沉降+回弹再压缩变形等值线图】。

E 倾斜指基础倾斜方向两端点的沉降差与其距离的比值；局部倾斜指砌体承重结构沿纵向 6m ～10m 内基础两点的沉降差与其距离的比值。

所以对于沉降差、倾斜、局部倾斜结果，用户可以通过软件的【两点沉降差】来自行检查。

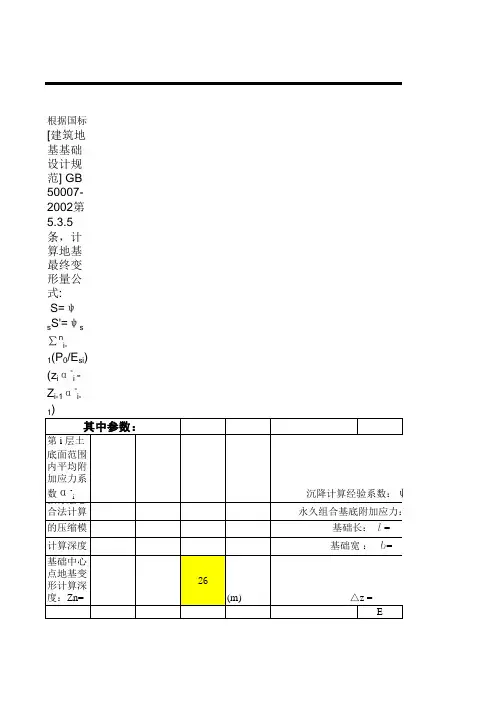
（2）沉降计算方法的规范规定 《地基规范》第 5.3.5 条计算地基变形时，地基内的应力分布，可采用各向同性均质线性变形体理论。

其最终变形量可按下式进行计算：np - -s = ψ s ,= ψ ∑(z αi - z αi -1) s si i -1i =1 Esi式中：s ——地基最终变形量(mm)；s′——按分层总和法计算出的地基变形量(mm)；ψs ——沉降计算经验系数，根据地区沉降观测资料及经验确定，无地区经验时可根据变形计算深度范围内压缩模量的当量值(E s )、基底附加压力按表 5．3．5 取值；n ——地基变形计算深度范围内所划分的土层数(图 5．3．5)； p 0——相应于作用的准永久组合时基础底面处的附加压力(kPa)；E si ——基础底面下第 i 层土的压缩模量(MPa)，应取土的自重压力至土的自重压力与附加压力之和的压力段计算；z i 、z i-1——基础底面至第 i 层土、第 i-1 层土底面的距离(m)；a i 、a i-1——基础底面计算点至第 i 层土、第 i-1 层土底面范围内平均附加应力系数，可按本规范附录 K 采用。

第三章土的压缩性与地基沉降计算填空题：1、地下水位的升降会引起土中自重应力的变化，地下水位升高则引起土体中的有效自重应力__________，地下水位下降引起土体中的有效自重应力__________。

2、计算自重应力时，地下水位以下的重度应取__________。

3、为了简化计算，基底压力常近似按__________分布考虑。

4、某均质地基，已知其重度γ＝17.6kN／m3，则地面下深度为3m处由上部土层所产生的竖向自重应力为__________kPa。

5、均布矩形荷载作用于地表，矩形荷载中心和角点的附加应力分别为σ0和σ1，则σ0和σ1的关系是__________。

6、在相同的压力作用下，饱和粘性土压缩稳定所需时间t1与饱和砂土压缩稳定所需时间t2的关系是__________。

7、若土的初始孔隙比为0.8，某应力增量下的压缩系数为0.3MPa-1，则土在该应力增量下的压缩模量等于__________。

8、按照土体前期固结压力与现有自重应力的关系，可将土分为正常固结土、__________和__________三大类。

9、从应力转化的观点出发，可以认为饱和土的渗透固结无非是：在有效应力原理控制下，土中孔隙压力消散和__________相应增长的过程。

10、在其他条件相同的情况下，固结系数增大，则土体完成固结所需时间的变化是__________。

11、常见的地基最终沉降量的计算方法有__________、__________和弹性力学法。

12、建筑物地基变形的特征有__________、__________、__________和__________四种类型。

选择题：1、自重应力在均匀土层中呈（）分布。

（A）、折线（B）、曲线（C）、直线（D）、均匀2、地下水位升高会引起自重应力（）。

（A）、增大（B）、减小（C）、不变（D）、不能确定3、某场地自上而下的土层分布为：第一层粉土，厚3m，重度Y为18kN／m3；第二层粘土，厚5m，重度为18.4kN／m3，饱和重度γsat=19.0kN／m3，地下水位距地表5m，则地表下6m 处的竖向自重应力等于（）。

向分层总和法计算基础中点最终沉降量案例分层总和法是一种常用的地基沉降计算方法，用于评估建筑物或结构物在不同地层中的沉降变形。

下面将通过一个案例来说明分层总和法的计算过程。

假设一些地基有3层土层，分别为上层A、中层B和下层C。

已知各层土层的厚度、压缩指数和应力增量。

要求计算在施工荷载作用下，地基的最终沉降量。

首先，我们需要了解各层土层的特性参数。

假设上层A的厚度为2m，压缩指数为0.2，应力增量为50kPa。

中层B的厚度为4m，压缩指数为0.3，应力增量为100kPa。

下层C的厚度为6m，压缩指数为0.4，应力增量为150kPa。

接下来，我们需要计算各层土层的压缩量。

根据分层总和法的计算公式，压缩量等于厚度乘以压缩指数。

所以，上层A的压缩量为2m*0.2=0.4m，中层B的压缩量为4m*0.3=1.2m，下层C的压缩量为6m*0.4=2.4m。

然后，我们需要计算各层土层的最终应力。

根据分层总和法的计算公式，最终应力等于施工前的初始应力加上应力增量。

上层A的最终应力为0+50kPa=50kPa，中层B的最终应力为0+100kPa=100kPa，下层C的最终应力为0+150kPa=150kPa。

接下来，我们需要计算各层土层的总压缩量。

总压缩量等于压缩量除以最终应力。

所以，上层A的总压缩量为0.4m/50kPa=0.008m，中层B的总压缩量为1.2m/100kPa=0.012m，下层C的总压缩量为2.4m/150kPa=0.016m。

最后，我们需要计算地基的最终沉降量。

最终沉降量等于各层土层的总压缩量之和。

所以，地基的最终沉降量为0.008m+0.012m+0.016m=0.036m。

综上所述，根据分层总和法的计算过程，我们得出了该地基在施工荷载作用下的最终沉降量为0.036m。

需要注意的是，这只是一个简单的案例，实际应用中可能存在更多的土层和复杂的土层特性，需要根据具体情况进行详细计算和分析。

YJK沉降计算的使⽤要点及案例YJK 基础沉降计算的使⽤要点及案例1 沉降计算的有关规范规定（1）沉降验算的规范规定问题1：哪些需要验算沉降《建筑地基基础设计规范》第 3.0.2 条规定“设计等级为甲级、⼄级的建筑物，均应按地基变形设计”，并规定六类情形下的丙类建筑物，“仍应作变形验算”。

是否需要进⾏基础沉降验算，软件不⾃动判断，由⽤户根据上述规范条件判断。

问题2：建筑物沉降验算满⾜要求的判断标准所谓地基变形验算，即要求地基的变形计算值在允许的范围内：≤[] （1）式中：[?]—地基的允许变形值，按《建筑地基基础设计规范》5.3.4 条取值。

《地基规范》表5.3.4 给出了建筑物的地基变形允许值，控制指标包括沉降量、沉降差、倾斜、局部倾斜。

《桩基规范》表5.5.4 给出了建筑桩基沉降变形允许值，控制指标包括沉降量、沉降差、倾斜、局部倾斜。

YJK 基础软件统⼀给出所有基础的沉降验算结果，见下图：沉降量应查看沉降等值线图，软件以等值线加数值的⽅式给出所有基础的沉降量计算结果。

注意两点：1）桩沉降是包括了⼟沉降及桩⾝压缩的总值；2）考虑⼟回弹再压缩情况（⼀般是基础埋深超过5 ⽶情况），沉降总值要查看【沉降+回弹再压缩变形等值线图】。

E 倾斜指基础倾斜⽅向两端点的沉降差与其距离的⽐值；局部倾斜指砌体承重结构沿纵向 6m ～10m 内基础两点的沉降差与其距离的⽐值。

所以对于沉降差、倾斜、局部倾斜结果，⽤户可以通过软件的【两点沉降差】来⾃⾏检查。

（2）沉降计算⽅法的规范规定《地基规范》第 5.3.5 条计算地基变形时，地基内的应⼒分布，可采⽤各向同性均质线性变形体理论。

其最终变形量可按下式进⾏计算：np - -s = ψ s ,= ψ ∑(z αi - z αi -1) s si i -1i =1 Esi式中：s ——地基最终变形量(mm)；s′——按分层总和法计算出的地基变形量(mm)；ψs ——沉降计算经验系数，根据地区沉降观测资料及经验确定，⽆地区经验时可根据变形计算深度范围内压缩模量的当量值(E s )、基底附加压⼒按表 5．3．5 取值；n ——地基变形计算深度范围内所划分的⼟层数(图 5．3．5)； p 0——相应于作⽤的准永久组合时基础底⾯处的附加压⼒(kPa)；E si ——基础底⾯下第 i 层⼟的压缩模量(MPa)，应取⼟的⾃重压⼒⾄⼟的⾃重压⼒与附加压⼒之和的压⼒段计算；z i 、z i-1——基础底⾯⾄第 i 层⼟、第 i-1 层⼟底⾯的距离(m)；a i 、a i-1——基础底⾯计算点⾄第 i 层⼟、第 i-1 层⼟底⾯范围内平均附加应⼒系数，可按本规范附录 K 采⽤。