梁拱组合体系桥地震响应敏感性参数分析

基于反应谱的梁拱组合体系地震反应影响研究【摘要】近代以来全球由于地震给人类生命和财产造成的非常严重的损失，也给人类带来了深刻的教训。

桥梁工程是抗震救灾后的的生命线上的重要工程，保证震后桥梁的正常通行是灾后救援和减小震后次生灾害的重要保障。

因此，在桥梁设计中必须进行桥梁的地震作用影响分析，预估桥梁的抗震性能。

确保桥梁的抗震性能能够满足设计和规范的要求，是保证地震中桥梁的安全的有效措施。

本文基于反应谱方法对梁拱组合体系桥梁的地震反应进行了分析研究。

【关键词】地震；桥梁工程；梁拱组合体系；地震反应引言地震是当今世界上人们面临的最大自然灾害之一。

全世界每年平均发生破坏性地震近千次，其中震级达7级或7级以上的大地震约十几次，给人类带来了极大的灾难，严重地威胁到人们的财产及生命安全[1]。

桥梁又是抗震救灾后的的生命线上的重要工程，保证震后桥梁的正常通行是灾后救援和减小震后次生灾害的重要保障[2]。

因此，在桥梁设计中必须进行桥梁的地震作用影响分析，预估桥梁的抗震性能。

确保桥梁的抗震性能能够满足设计和规范的要求，保证地震中桥梁的安全。

1 工程背景该桥是某新建铁路工程中的一座1-80m下承式简支钢管混凝土拱桥，跨越高速公路，全长为82.50m。

梁拱组合桥位于平坡、直线上，主拱轴线为二次抛物线，桥面体系采用双梁体的纵横梁体系，桥顶面宽16.2m。

拱肋采用钢管混凝土哑铃形拱，全桥共设11对吊杆。

为增加拱肋横向刚度，在6#吊杆处设置横撑，在3#、3’#吊杆处设置k撑。

总体布置见下图1：图1全桥总体布置图（cm）2 有限元模型桥梁结构是一空间结构，在静力分析时习惯上将空间结构简化成平面杆系结构来进行计算，活载的空间效应用横向分布系数或偏载系数来表达。

本桥通过有限元软件midas2006建立有限元模型。

主梁为双纵梁体系，两根主纵梁中间设置四根小纵梁。

中间在横向采用横隔板相连，故有限元模型将梁系结构用梁格法按格子梁模式离散，即将纵梁和横隔板简化为纵横交错的梁单元。

某桥梁地震响应时程分析及建议的抗震措施桥梁是城市交通系统中重要的组成部分，其安全性对城市的交通运行和人民的生命财产安全有着重要的影响。

地震是破坏性极大的自然灾害，对桥梁的抗震性能提出了更高的要求。

本文将围绕桥梁地震响应时程分析及建议的抗震措施展开讨论。

首先，桥梁地震响应时程分析是评估桥梁在地震作用下的结构响应和破坏程度的重要手段。

通过对地震波进行时程分析，可以得出桥梁在地震作用下的加速度、速度、位移等响应曲线，从而对桥梁结构的安全性进行评估。

在进行桥梁地震响应时程分析时，首先需要获取地震波数据。

根据所在地区的地震活动趋势，选择适当的地震波数据进行分析。

其次，需要进行有限元模型的建立。

将桥梁结构抽象成一组节点和单元，并根据实际情况给予相应的边界条件和约束条件。

然后，进行模型的参数修正工作。

通常情况下，需要根据实测的数据对模型进行调整，以更好地与实际情况匹配。

最后，进行地震响应时程分析。

利用地震波数据进行模拟计算，得出桥梁结构在地震作用下的响应。

根据桥梁地震响应时程分析的结果，可以得出桥梁结构存在的问题，并提出相应的抗震措施。

以下是一些常见的桥梁抗震措施建议。

1.给予桥梁足够的纵向和横向刚度。

增加桥梁的刚度可以提高其自振周期，降低地震作用下的位移和变形。

可以通过加固桥梁梁、柱和墩体的结构，增加构件截面尺寸或采用高强度材料等方法来提高刚度。

2.提高桥梁的耗能能力。

在地震作用下，桥梁结构会受到较大的地震力，耗能能力不足的桥梁容易发生破坏。

可以通过设置减震装置、阻尼器或摆锤等来改善桥梁的耗能能力，减小地震作用下的结构响应。

3.加固桥梁节点和连接部位。

桥梁的节点和连接部位是桥梁结构的薄弱环节，地震作用下容易发生破坏。

可以采用加固板、钢板箍或碳纤维增强等方式来增强节点和连接部位的抗震性能。

4.建立桥梁监测系统。

通过在桥梁上设置加速度计、应变传感器等监测设备，可以实时监测桥梁的结构响应和变形情况，及时发现结构的异常，采取相应的维修和加固措施。

多跨刚构—连续组合梁桥参数敏感性分析及施工监控
近些年来,多跨刚构-连续组合梁桥在地形起伏、墩高差异较大的高墩大跨结构中广泛应用。

但作为一种复杂的超静定结构,多跨刚构-连续组合梁桥施工工艺复杂,工期长,施工过程影响结构状态的参数较多,比如结构的设计参数、温度荷载、混凝土收缩徐变效应、合龙顺序等,造成实际成桥状态与设计理想状态出现偏差,影响结构运营阶段的正常使用。

因此,有必要对多跨刚构-连续梁桥实际施工过程进行监测控制,掌握桥梁的实际工作状态,并对影响因素进行参数敏感性分析,进而对控制参数进行适当调整,指导实际施工,满足合理成桥状态的线形和受力要求。

本文以内蒙古准兴黄河大桥主桥为依托工程,进行了混凝土容重γ、弹性模量E以及预应力损失值三项在内的设计参数的敏感性分析,同时引入敏感度系数S识别影响多跨刚构-连续
组合梁桥最大悬臂状态以及成桥状态的主要设计参数、次要设计参数;进行混凝土收缩徐变效应的影响分析,研究发现成桥10年全桥整体下挠但各跨下挠量略
有不同,其中成桥5年内主梁下挠增长较快,随着时间的增长混凝土收缩徐变对
结构的长期变形影响较小;进行了温度荷载影响分析,得出了整体升温、整体降温、梯度升温、梯度降温四种温度荷载工况下结构的应力和位移状态,进而提出控制温度荷载影响的措施;分析不同合龙顺序对多跨刚构-连续组合梁桥成桥状态实
际位移和应力的影响,并确定合理的合龙方案。

在以上基础上,对内蒙古准兴黄河大桥主桥左幅施工监控方案进行了阐述,
包括监控内容、监控方法、监控系统等。

最后,将线形和应力的实测结果与理论分析结果比对,给出监控结论。

桥梁结构的地震响应分析与减震控制地震是世界各地广泛存在的自然灾害，造成了巨大的人员伤亡和财产损失。

对于桥梁结构而言，地震响应是一个重要的研究领域。

本文将就桥梁结构的地震响应分析和减震控制进行探讨。

一、桥梁结构的地震响应分析地震对桥梁结构的影响是通过结构的动力响应来反映的。

地震激励作用下，桥梁结构会发生振动，并且会带来很大的变形和应力。

为了对桥梁结构的地震响应进行分析，需要考虑以下几个因素：1. 地震输入：地震输入是指地震波的特征参数，包括地震波的频谱特性、持时和地震波的峰值加速度等。

2. 桥梁的动力特性：桥梁的动力特性包括自振频率、阻尼比和模态形态等。

自振频率越低，桥梁结构对地震波的响应越明显；而阻尼比越高，桥梁结构的减震效果越好。

3. 结构的非线性效应：由于桥梁结构大变形和应力，会引起结构的非线性行为，如塑性变形、裂缝扩展等。

这些非线性效应对结构的地震响应具有重要的影响。

通过对桥梁结构的地震响应分析，可以评估结构的安全性和破坏性，并为减震控制提供依据。

二、桥梁结构的减震控制为了降低桥梁结构在地震中的响应，减震控制技术被广泛应用于桥梁工程中。

1. 传统的减震控制技术：传统的减震控制技术包括增加结构的刚度和强度、采用隔震支座等。

增加结构的刚度和强度可以提高结构的抗震能力，但也增加了工程成本。

隔震支座可以有效隔离地震输入，减小结构的地震反应。

然而，传统减震控制技术对于大跨度桥梁结构效果有限，难以满足高抗震性能的要求。

2. 新型的减震控制技术：新型的减震控制技术主要包括液压减震装置、摩擦阻尼器和智能材料等。

液压减震装置通过可控的液压阻尼来消耗结构的动能，起到减震的作用。

摩擦阻尼器采用摩擦阻尼力来减小结构的振动，降低地震反应。

智能材料可以根据外界的激励实时调整自身的特性，从而降低结构的振动。

新型的减震控制技术具有很好的效果，能够提高桥梁结构的抗震能力和安全性。

然而，这些技术的应用需要充分考虑桥梁结构的特点和使用环境，以保证其可靠性和经济性。

桥梁设计中的地震响应分析与减震控制桥梁是人类社会固有的重要交通设施之一，自古以来就有着跨越河流、峡谷等特殊地理环境的需要。

然而，地震是一个不可预知、不可避免的自然灾害，其对桥梁的破坏是不可估量的。

因此，在桥梁的设计、建设和维护中，地震响应分析和减震控制显得尤为重要。

一、桥梁地震响应分析桥梁在地震中的响应主要表现为结构的变形、应力的分布、动态特性的变化等。

因此，为了准确评估桥梁在地震中的破坏情况，需要进行地震响应分析。

地震响应分析主要包括静力分析和动力分析两种方法。

静力分析是建立在弹性理论基础上的方法，它假设桥梁在地震作用下的响应具有线性的特性，且桥梁结构的变形是可逆的。

这种方法可以快速计算出桥梁在地震中的内力、位移等参数，然而它无法刻画桥梁在非线性时的响应情况。

动力分析则是基于桥梁结构的实际响应情况进行的，它可以准确评估桥梁在地震中的响应，包括结构的变形、应力的分布、动态特性的变化等。

目前常用的动力分析方法主要包括时程分析、反应谱分析等。

时程分析可以模拟不同地震强度下桥梁的响应情况，而反应谱分析则可以在给定地震作用下，计算出桥梁的动态特性并评估其响应情况。

二、桥梁减震控制技术为了减小桥梁在地震中受到的破坏，需要采用有效的减震控制技术。

目前常用的桥梁减震控制技术主要有被动控制和主动控制两种。

被动控制是指在桥梁结构中预制加装减震装置，利用减震器等器件来吸收地震能量并减小桥梁结构的振动响应。

被动控制技术具有结构简单、成本低等优点，但是其减震效果受到地震作用的影响较大，而且其减震器等器件在使用过程中容易发生疲劳或损坏。

主动控制是指利用主动控制装置来控制桥梁结构的振动响应，在地震发生后能够快速响应并调整结构的动态特性。

主动控制技术具有减震效果好、控制精度高等优点，但是其设计成本较高，控制系统也较为复杂，运行维护和管理难度较大。

此外，还有一种较为常用的混合控制技术，即被动控制与主动控制相结合的混合减震控制。

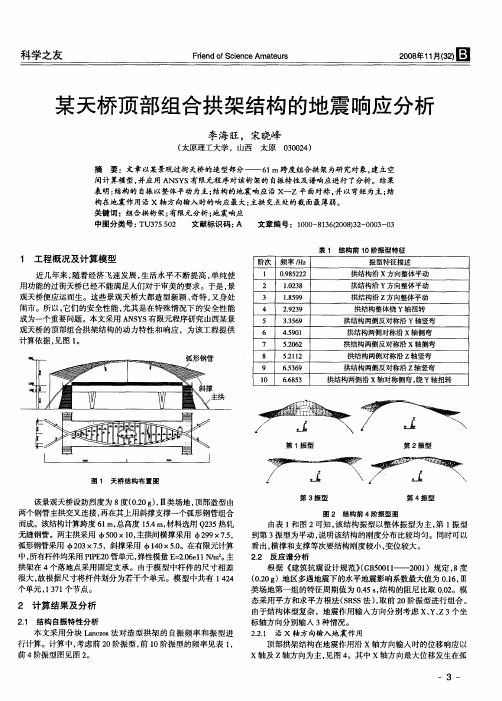
戴河大桥钢管混凝土系杆拱桥地震响应分析摘要：针对戴河大桥主要振型是拱肋横向振动和主梁的竖向振动特点，采用ANSYS软件的瞬态分析模块，对戴河大桥输入地震波加速度时程进行计算。

为便于与反应谱分析结果对比，本文选取天津波、迁安波和El-Centro波经调幅后，分别按横桥向水平+0.67竖向输入，比较结构的动力响应。

得出如下结论：在横向水平地震作用下，拱肋横向变形较大，而主梁变形相对较小；在竖向地震作用下，主梁竖向位移较大；最大轴力、剪力和弯矩都出现在拱脚和梁端位置，说明拱脚和梁端地震内力很大，是抗震设计中的危险截面。

拱顶横向位移和主梁跨中竖向位移较大，这与反应谱分析的结果是一致的。

三种工况横向比较，除拱顶横向位移等少数项目外，这三种工况下各主要控制断面的位移峰值相差不大，其中天津波所得各项数值都大于另外两种工况。

三种时程分析工况所得结果与反应谱分析结果有较大差异。

天津波所得结果稍接近于反应谱分析结果。

关键词：钢管混凝土拱桥；地震响应；反应谱分析；时程分析1 引言钢管混凝土技术发展以来，国内外首先大量开展对钢管混凝土构件特别是建筑结构中的柱动力特性的研究。

通过试验与有限元数值计算相结合，对钢管混凝土构件的滞回特性及延性性能取得了一些研究成果[1]-[4]。

比如哈建大等单位通过研究建立了平面的压弯构件的弯矩—曲率、轴力—位移恢复力模型。

而拱桥体系呈现明显空间特性，受力特征有别于普通柱，因此，桥梁工程相关领域的学者有所针对地对拱结构展开了一些专门研究。

90年代以来，伴随着钢管混凝土拱桥建设的热潮，对于钢管混凝土系杆拱桥的动力性能和地震响应研究也大量开展。

这些研究大多都是结合具体工程进行的[5]-[9]。

这里面存在理论研究滞后于实际应用的问题，往往在较大跨径的钢管混凝土拱桥建成以后才对其承载能力、整体稳定性、抗震性能等进行研究。

尽管如此，钢管混凝土系杆拱桥的地震响应研究还是取得大量的成果。

钢管混凝土拱桥动力特性方面的研究，主要集中在横撑的形式、刚度和布置对拱桥动力参数的影响，对于其它参数对钢管混凝土拱桥的动力性能影响研究较少；同时，对非线性问题对钢管混凝土系杆拱桥的抗震能力研究以及对考虑桩-土-结构相互作用等方面的研究都还不够成熟。