2021-5-10
7
xi' fi (t, x1,, xn ) i 1,2,, n
设微分方程组有 n 个首次积分
1(t, x1, x2 ,, xn ) c1,,n(t, x1, x2 ,, xn ) cn
如果在某区域内它们的Jacobi行列式
1
x1
1
x2
1
xn
D(1,,n )
D(x1,, xn )
经适当组合化为一个可积分的微分方程. 这个方程的未知函数可能是方程组中
几个未知函数组合形式. 积分可以得到未知函数组合形式的解, 该方程为一个原方程组的首次积分.
2021-5-10
5
例 4 求解方程组 dx y, dy x
dt
dt
解 将两个方程相加得 d (x y) x y
dt
以 x y 作为一个未知函数,对上式积分得
2021-5-10
13
小结:寻找首次积分的方法(技巧性强)
为了求得首次积分,通常把如下方程组
xi' fi (t, x1,, xn ) i 1,2,, n
写成对称形式 d x 1 = d x 2 = ... = d x n = d t
f1
f2
fn
1
方法1 (积分因子法)利用比例性质化分母为零,分子 为某一函数的全微分形式。(教材P350)
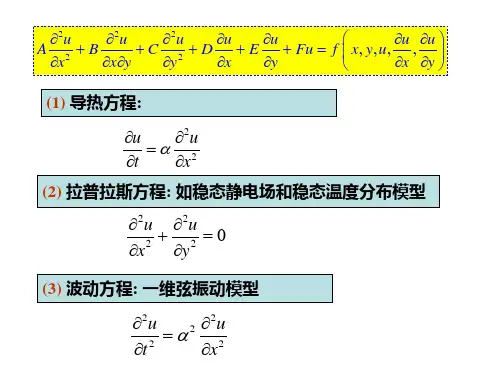
2u x 2
x2
2u y 2
1
于是偏微分方程 u x
2u xy
3u y3
f
(x, y)便可简单
记为L[u] f 或Lu f .
算子L若满足:L[au bv] aL[u] bL[v] 其中,a,b为常数;u, v为函数,则称L为线性算子。