当前位置：文档之家 › 112简谐运动的描述 ppt课件

112简谐运动的描述 ppt课件

  • 格式：ppt
  • 大小：8.33 MB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

简谐运动的描述(高中物理教学课件)完整版

简谐运动的描述(高中物理教学课件)完整版

四.简谐运动的表达式
简谐运动的表达式：x＝Asin（ωt＋φ）
位移 振幅
时刻 初相位
圆频率 ω＝2π/T＝2πf
也可以写成：x Asin(2 t )
T
相位
根据一个简谐运动的振幅、周期、初相位，可以知道做 简谐运动的物体在任意时刻的位移，故振幅、周期、初 相位是描述简谐运动特征的物理量。
三角变换
因为 2 ， T 2 2 m
T
k
振动系统本身性质决 定的。
同时放开的两个小球振动步调总是 一致，我们说它们的相位是相同的；
而对于不同时放开的两个小球，我 们说第二个小球的相位落后于第一个 小球的相位。
如何定量的表示相位呢？
三.相位
1.相位：物理学中把（ωt＋φ）叫作相位，其中φ 叫初相位，也叫初相。 由简谐运动的表达式x＝Asin（ωt＋φ）可以知道， 一旦相位确定，简谐运动的状态也就确定了。 2.相位差：两个具有相同频率的简谐运动的相位 的差值。 如果两个简谐运动的频率相同，其初相分别是φ1 和φ2，当φ1>φ2时，它们的相位差是Δφ＝(ωt＋φ1) －(ωt＋φ2)＝φ1－φ2此时我们常说1的相位比2超前 Δφ，或者说2的相位比1落后Δφ。
x甲 0.5sin(5t )cm 或者x甲 0.5sin 5tcm
x乙
0.2 sin(2.5t
2
)cm
或者x乙 0.2 cos 2.5tcm
注意： 振动物体运动的范围是振幅的两倍。
二.周期和频率
做简谐振动的振子，如果从A点开始运动，经过O点运动到Aˊ点再 经过O点回到A点，这样的过程物体的振动就完成了一次全振动。 如果从B点向左运动算起，经过O点运动到Aˊ点，再经过O点回到 B点，再经A点返回到B点时，这样的过程也是一种全振动。

简谐运动的描述ppt课件

简谐运动的描述ppt课件

最低点，因此周期应该约是T＝1.2 s.因此③、④错误.本题
应选C.
8.某质点做简谐运动，其位移随时间变化的关系式为x=
Asin t，则质点(
4
)
A.第1 s末与第3 s末的位移相同 B.第1 s末与第3 s末的速度相同 C.3 s末至5 s末的位移方向都相同 D.3 s末至5 s末的速度方向都振幅之比、各自的频率以及它们的相 2
【解析】根据x=Asin(ωt+ )得：A1=4a，A2=2a.A1∶A2=4a∶
2a=2∶1,由ω1=ω2=4πb及ω1=ω2=2πf得：f1=f2=2b,它们的 相位差是：
1 (4πbt+ 3 π)-(4πbt+ π)=π 2 2
【典例1】一个做简谐运动的质点，其振幅是4 cm，频率是 2.5 Hz，该质点从平衡位置经过2.5 s后的位移大小和路程是 ( A．4 cm，24 cm C．0，24 cm B．4 cm，100 cm D．0，100 cm )
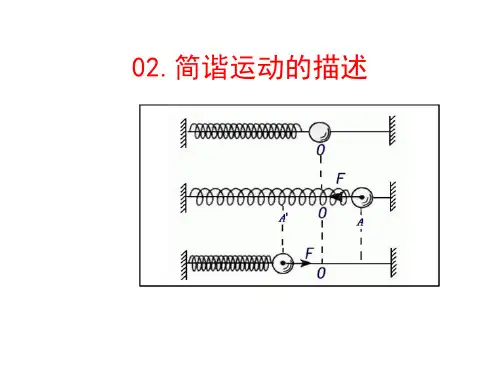
【解题指导】先作出简谐运动的模型(如图所示)
(1)根据频率与周期的关系计算周期； (2)根据题中给出的运动时间2.5 s找出振子所在的位置及时 间与周期的关系．
【解析】选A、D.由表达式x=Asin t知，ω= ，简谐运动的
4 4 2 周期T= =8 s.表达式对应的振动图象如图所示.
2 质点在1 s末的位移x1=Asin( ×1)= A 4 2
质点在3 s末的位移x3=Asin( ×3)= 2 A，故A正确；由前面
计算可知t=1 s和t=3 s质点连续通过同一位置，故两时刻质
关
【解析】选B、C．简谐运动的频率与物体运动的快慢没有关
系，描述物体运动的快慢用速度，假如说物体振动过程中最 大速度越大，也不能说明它的频率越大．振动的越快和运动 的越快意义是不同的，故A错误；简谐运动的物体在一个周期 内速度的方向改变两次，频率越高，单位时间内所包含的周 期个数越多，速度方向变化的次数就越多，故 B、C正确；弹 簧振子的固有频率与物体通过平衡位置的速度没有关系，它 由振动系统的固有量振子的质量m和弹簧的劲度系数k决定,故

简谐运动及其描述.ppt

简谐运动及其描述.ppt
x Asin(t )
振幅 圆频率
初相位 相位
2 2f
T
x Asin(2 t ) Asin(2ft )
T
振幅
周期
初相位 相位
频率
说一说
相位 t 的单位应该是什么？
国际单位：弧度
1、一个物体运动时其相位变化多少就意 味着完成了一次全振动?
2、甲和乙两个振动周期相同的简谐运动 的相差为 ，意味着什么?
4bt
3 2
ቤተ መጻሕፍቲ ባይዱ
4bt
1 2
A、B之间的相位差是 （
2
）
注：B是超前
BA
图示为某简谐运动的位移——时间图象。 根据图象写出该简谐运动的位移随时间变 化的关系式
x＝４sin(10πt- π/2) cm
小结
一、描述简谐运动的物理量
1、振幅A：振动物体离开平衡位置的最大距离 2、周期T：完成一次全振动所需要的时间
子
的
OA = OB = A
再
研
2cm
究 问题1：该弹簧振子的振幅多大？
问题2：该弹簧振子到达A点时离O点的距离？
描述简谐运动的物理量
弹 （二）、周期T（频率f）: 簧 定义：振子完成一次全振动所经历的时间。
振
子
的 一次全振动：振动物体从某一初始状态开始，
再
再次回到初始状态（即位移、速度、加速度均 与初态完全相同）所经历的过程。
5t0
6t0
17.7
20.0
11t0
-17.8
12t0
-20.0
坐标原点O－平衡位置 横坐标－振动时间t
纵坐标－振子相对于平衡位置的位移
思考：由此图象猜想弹簧振子的位移 随时间的变化规律？

11.1《简谐运动》PPT课件

11.1《简谐运动》PPT课件

想一想
一个完整的全振动过程，有什 么显著的特点？
在一次全振动过程中，一定是
振子连续两次以相同速度通过同一
点所经历的过程。（强调方向性）
2021
33
周期的可能影响因素
弹 簧 振 子 的 再 研 究
2021
34
周期的可能影响因素
弹
簧
振
如何测时间？
子 的
在什么位置测时间？
再
研
结论：周期大小与
究
振幅无关！
2021
35
看一看 两个振子的运动快慢有何不同？
2021
36
2、周期和频率
1)、描述振动快慢的物理量 2)、周期T：做简谐运动的物体完成一次全振
动所需的时间，单位：s。
3)、频率f：单位时间内完成的全振动 的次数，单位：Hz。
4)、周期和频率之间的关系：
f=1/T
5)、周期越小，频率越大，运动越快。
D．O至B位移为负、速度为负
2021
26
简谐运动的特点：
1、简谐振动是最简单、最基本的运动，简谐振 动是理想化的振动。
2、加速度与位移方向相反，总是指向平衡位置 。
3、简谐运动是一种理想化的运动，振动过程中 无阻力，所以振动系统机械能守恒。
4、简谐运动是一种非匀变速运动。 5、位移随时间变化关系图是正弦或余弦曲线.
1位移大小相等方向相反2速度大小相等方向可能相同也可能相反3加速度大小相等方向相反4从平衡位置到达这两个或从这两个点直接到达平衡位置的时间相等对称关系2021471从图像中可直接读出在不同时刻的位移值从而知道位移x随时间变化的情况2可以确定振幅3可以确定振动的周期和频率4可以用作曲线上某点的切线的办法确定各时刻的速度大小和方向5由于简谐运动的加速度和位移大小成正比方向相反可以根据图像上各时刻的位移变化情况确定质点加速度的变化情况202148202149如果两个摆球振动的步调一致称为同相

简谐运动的描述ppt课件

简谐运动的描述ppt课件
2.2
简谐运动的描述
目录
CONTENTS
1
简谐运动的表达式
2
描述简谐运动的物理量
3
简谐运动的周期性和对称性
4
简谐运动振幅与路程的关系
有些物体的振动可以近似为简谐运
动，做简谐运动的物体在一个位置附近
不断地重复同样的运动。如何描述简谐
运动的这种独特性呢？
知识回顾：
简谐运动的位移图像是一条正弦曲线。
全振动的特点：①位移和速度都会到初状态 ②路程等于4A
②周期：做简谐运动的物体完成一次全振动所需要的时间，用T表示，
单位：s.
③ 频率：单位时间内完成全振动的次数，用f表示，单位：Hz.
周期T与频率f的关系是T＝
知道即可：弹簧振子的周期由哪些因素决定?
周期公式： T 2
m
k
弹簧振子周期（固有周期）和频率由振动系统本身的因素决定（振子的质量m和弹
②若△ = 2 − 1＜0，振动2的相位比1落后△ 。
4.同相与反相：
（1）同相：相位差为零



△ = 2( = 0，1，2， … )


（2）反相：相位差为
△ = (2 + 1)( = 0，1，2， … )

A与B同相
A与C反相
A与D异相
相位差90°
＝（ ＋ ）
一、简谐运动的表达式
相位
x A sin(t )
振幅
圆频率
初相位
二、描述简谐运动的物理量
＝（ ＋ ）
1.振幅：（1）定义：振动物体离开平衡位置的最大距离。
振幅
O
振幅
（2）物理意义：振幅是描述振动强弱的物理量。

11.2简谐运动的描述 (共13张PPT)

11.2简谐运动的描述 (共13张PPT)
第十一章机械振动
二.简谐运动的描述
描述简谐运动的物理量
振幅--A
（1）定义:振动物体离开平衡位置的最大距离。
（2）物理意义：振幅是描述振动强弱的物理量。
振幅的2倍表示振动物体运动范围的大小。
（3）单位：在国际单位制中，振幅的单位是米
振幅和位移的区别
(1)振幅等于最大位移的数值。 (2)对于一个给定的振动，振子的位 移是时刻变化的，但振幅是不变的。 (3)位移是矢量，振幅是标量。
• 2．振幅、位移和路程的关系
振幅 振动物体离开 位移 从平衡位置指向 路程 运动轨迹的长 度
定义
平衡位置的最
大距离 标量 在稳定的振动系
振子所在位置的
有向线段 矢量 大小和方向随时 间做周期性变化
矢标性 变化
标量
随时间增加
统中不发生变化
(1)振幅等于位移最大值的数值；(2)振子在一 联系 个周期内的路程等于4个振幅；而振子在一个 周期内的位移等于零。
2、意味着乙总是比甲滞后1/4个周期
A
P ′
O P 平衡位置
A′
半个周期后振子到了P′点--P关于O的对称点
半个周期内的路程是多少呢？ 2A
弹簧振子在四分之一周期内的路程是A吗？
V
A
P′
O 平衡位置
P
有可能是A，有可能大于A，有可能小于A. 总结：弹簧振子在一个周期内的路程一定 是4A，半个周期内路程一定是2A，四分之 一周期内的路程不一定是A。
周期和频率
（1）周期（T）：做简谐运动的物体完成一次全 振动所需要的时间，叫做振动的周期，单位：s。 （2）频率（f）：单位时间内完成的全振动的次 数，叫频率.单位：Hz，1Hz=1s-1。 物理意义：周期和频率都是表示物体振动快慢的 物理量，周期越小，频率越大，表示物体振动越 快，周期与频率的关系：T＝(用公式表示)． （3）周期和频率之间的关系：ห้องสมุดไป่ตู้＝1/f。 简谐运动的周期和频率由振动系统本身的因素决定 （振子的质量m和弹簧的劲度系数k ），与振幅无关

11.1《简谐运动》课件 (共28张PPT)


3．如图所示，轻质弹簧下端挂重为30N的物体A，弹簧 伸长了3cm，再挂重为20N的物体B时又伸长2cm，若将 连接A和B的连线剪断，使A在竖直面内振动时，下面结论 正确的是（ AD ） A．振幅是2cm B．振幅是3cm C．最大回复力是30N D．最大回复力是20N
课后作业：试证明A在竖直方向的振动就是简谐振动。
1、质点离开平衡位置的最大位移？ 2、1s末、4s末、10s末质点位置在哪里？ 3、1s末、6s末质点朝 哪个方向运动？ 3 4、质点在6s末、14s 末的位移是多少？ O 5、质点在4s、16s内 通过的路程分别是多 -3 少？ 8 x/m
16
t/s
1、某一弹簧振子的振动图象如图所示，则由 图象判断下列说法正确的是（ A B ） A、振子偏离平衡位置的最大距离为10cm B、1s到2s的时间内振子向平衡位置运动 C、2s时和3s时振子的位移相等，运动方向也 相同 D、振子在2s内完成一次往复性运动
3.知识回顾：胡克定律
在弹簧发生弹性形变时，弹簧振子的回复力 F与振子偏离平衡位置的位移x大小成正比，且方 向总是相反，即：
F kx
这个关系在物理学中叫做胡克定律 式中k是弹簧的劲度系数。负号表示回复力 的方向跟振子离开平衡位置的位移方向相反。
4.简谐运动：
定义:物体所受的力与它偏离平衡位置的位移大小 成正比，并且总指向平衡位置，则物体所做的运动叫做 简谐运动。 说明:判断是否作简谐振动的依据是
光滑斜面
6.简谐运动的实例
简谐运动是最简单、最基本的振动。
复习：
x
x
（1）位移：振动中的位移x都是以平衡位置为起点的，因此，方向 就是从平衡位置指向末位置的方向，大小就是这两位置间的距离， 两个“端点”位移最大，在平衡位置位移为零。 （2）回复力：

物理人教版(2019)选择性必修第一册2.2简谐运动的描述(共33张ppt)

x Asint
月相：不同的月相可以 表示月亮处于不同的状 态，可以反映出月亮处 于不同的位置，月相随 时间的变化规律可以反 映处月亮位置随时间变 化的规律
把简谐运动等效为一个圆周 运动，物体在不同位置所对 应的相位实际上是圆周运动 的“相位角”
月相变 化本质 上也是 角度的 变化
如图所示，并列悬挂两个相同的弹簧振子，分别将小球A、小球B向下 拉至P、Q位置，此时两球离开平衡位置的距离分别为x和1.5x（均在 弹簧弹性限度范围内）。先把小球A由静止释放，当A第一次到达平衡 位置时，由静止释放小球B，则（ ） A．小球A到达最高点时，小球B还没有到达平衡位置 B．在平衡位置时，小球A与小球B的动能相等 C．运动过程中，小球A和小球B的速度不可能相等 D．小球B比小球A总是滞后四分之一个周期
某同学看到一只鸟落在树上树枝上的P处，树枝
在10s内上下振动了6次，鸟飞走后他把50g的砝码
挂在P处，发现树枝上下振动了12次，换成500g
的砝码后，他发现树枝在15s内上下振动了6次，
你估计鸟的质量最接近于（B ）
A.50g B.200g C.500g
D.600g
3.相位
描述周期性运动的物体在各个时刻所处 状态的物理量.
T
x Asin 2 t
T
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动，
BC相距20cm，某时刻振子处于B点，经过0.5s，首次到达
C，则下列说法正正确的是（ C）
A.振幅为20cm B.振子的周期为2s C.振子5s内的路程为200cm D.振子在3s内的位移为120cm
一个质点做简谐振动的图像如图所示，下列判断中正确 的是（ ） A．在t＝4×10－2s时，质点速度达到最大值 B．振幅为2×10－3m，频率为50Hz C．质点在0到1×10－2s的时间内，其速度和加速度方向 相同 D．该简谐振动的方程为x＝0.2cos（50πt）cm

高中物理课件-11-2简谐运动的描述(市级公开课).ppt

简谐运动的位移和时间的关系可以 用图象来表示为正弦或余弦曲线，如将 这一关系表示为数学函数关系式应为：
x Asin(t )
简谐运动的表达式 x Asin(t )
振动方程中各变量的含义：
1、 A 代表物体振动的振幅.
2、 叫做圆频率，表示简谐运动的快
慢。它与频率之间的关系为： =2f来自3、“ t+” 这个量就是简谐运动的相 位，它是随时间t不断变化的物理量， 表示振动所处的状态. 叫初相位，简 称初相，即t=0时的相位。
１、描述简谐运动的物理量——振幅、 周期、频率和相位。 振幅是描述振动强弱的物理量；
周期和频率都是用来表示振动快慢的 物理量。 相位是表示振动步调的物理量 ２、简谐运动的表达式为： x=Asin（ωt+φ ）
练习１： 一个质点作简谐运动的振动图像如图5-15 所示．从图中可以看出，该质点的振幅A= _0._1m，周期Ｔ=0_._4 s，频率f=_2._5Hz，从 t=0开始在△t=０.5s内质点的位移 _0_.1，m
全振动:一个完整的振动过程称为 一次全振动
一次全振动是简谐运动的最小单元， 振子的运动过程就是这一单元运动 的不断重复。
２１、、弹若簧从振振子子完经成过一C向次右全起振，动经的过路 怎程样与的振运幅动之才间叫存完在成怎一样次的全关振系动？？
二、周期和频率
①周期：做简谐运动的物体完成一次 全振动所需要的时间，叫做振动的 周期，单位：s。
②频率：单位时间内完成的全振动的 次数，叫频率。单位：Hz，1Hz=1s-1。
③周期和频率之间的关系：Ｔ＝1/f。
弹簧振子的周期与哪些因素有关？ 猜想：弹簧振子的振动周期可能由 哪些因素决定？
设计实验：
①实验过程中，我们应该选择哪个位 置作为计时的开始时刻？

11.2 简谐运动的描述—人教版高中物理选修3-4课件(共21张PPT)

解析 (1)若质点从O点向右运动到M点， 如甲、乙图所示
O→M→A历时0.18s 根据对称性可得到周期T1＝4×0.18 s＝0.72 s
(2)若质点从O点向左运动到M点，如丙图所示
由O→A→M历时t1＝0.13 s 由M→A历时t2＝T20＝ .0543s，(t1＋t2 )＝0.24 s
解析
x＝Asin(ωt＋φ)
振幅之比＝ A1 4a 2 :1
A2
两者频率均为： f
2a
4 b 2b
2 2
两者相位差为： =A B
3
22
两振动为反相
课堂练习 6、一质点在平衡位置O附近做简谐运动，从它经过平衡位置起 开始计时，经0.13 s质点第一次通过M点，再经0.1 s第二次通过 M点，则质点振动周期是多少？
A．从B→O→C→O→B为一次全振动 路程为4个振幅 B．从O→B→O→C→B为一次全振动 C．从C→O→B→O→C为一次全振动 D．OB的大小不一定等于OC
一定
课堂练习 5＋、3两2)个，简求谐它运们动的分振别幅为之x比1＝，4各as自in(的4π频bt率＋，2)以和及x2它＝们2a的sin相(4位πb差t 。
振子进行一次完整的振动（全振动）所经历的时间
一、描述简谐运动的物理量
3、相位
位置
用来描述周期性运动在 各个时刻所处的不同状 态．其单位是弧度(或度)
一、描述简谐运动的物理量
例1、(多选)一质点做简谐运动，其位移x与时间t的关系图象如图所示，由
图可知( C )
A．质点振动的频率是4 Hz
f＝0.25Hz
2s它第二次经过M点；则质点第三次经过M点所需要的时间是
（
）
A、8s CD B、16s
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
11.2 简谐运动的描述
2020/11/29
1
一、振幅，周期和频率
演示
上面所标的两段A有何特点？代表什么？
2020/11/29
2
精品资料
• 你怎么称呼老师？
• 如果老师最后没有总结一节课的重点的难点，你 是否会认为老师的教学方法需要改进？
• 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭
增大 减小 增大
向右 向右 增大 减小
向左 增大
向左 向右 向右
减小 增大 减小
2020/11/29
23
总结：做简谐运动的物体，在通过对称 于平衡位置的AB两个位置时，相对应的 各个各个物理量具有怎样的关系？
1、位移大小相等，方向相反 2、速度大小相等，方向可能相同，也可 能相反
3、加速度大小相等，方向相反 4、从平衡位置到达这两个或从这两个点 直接到达平衡位置的时间相等
演示
①与振幅无关。
②与弹簧有关，劲度系数(回复系数)越大，周期越小。
2020/11/29
9
• 简谐运动的周期和频率由振动系统 本身的因素决定，与振幅无关
• 与振子质量有关，质量越大，周期 越大
2020/11/29
10
四、相位及简谐运动的表达式
2020/1是表示物体振动步调的物理 量,用相位来描述简谐运动在一个 全振动中所处的阶段。
②振幅是标量，位移是矢量
③振幅是偏离平衡位置的最大距离，位移是偏离平衡位置的 距离。位移最大值的大小就是振幅
2.周期与频率 ①都是反映振动快慢的物理量
如何反映？两者有何关系？
②2两020者/11/互29 为倒数。即: T=1/f
8
三、固有周期和固有频率
周期和频率都反映振动快慢，那么它们与哪些因素有关呢？
运动快慢与振动快慢有区别吗？
V→运动快慢 ？→振动快慢
2020/11/29
5
一、振幅，周期和频率
2.周期 ①全振动：振动物体以相同速度相继通过 同一位置所经历的过程叫做一次全振动。
②做简谐运动的物体完成一次全振动所花 的时间叫做一个周期，是用来反映物体振 动快慢的物理量。
③周期的单位是s，常用符号是T。
3.“ t+” 叫简谐运动的相位.表示简谐 运动所处的状态.
叫初相,即t=0时的相位.
2020/11/29
17
2、简谐运动的表达式 相位
xAsi nt ()
振幅
圆频率 2 2f 初相位
T
xA si2 n t( )A si2 n f ( t)
T
2020/11/29
18
五、振子的路程和位移
做简谐运动的物体在任意一个周期内通过的路程是多少？ ①无论从什么位置开始计时，物体在一个周期内 通过的路程均为4A
意味着乙总是比甲滞后1/4个周期或1/4次全振动
2020/11/29
15
2、简谐运动的表达式
简谐运动的位移-时间关系 振动图象：正弦曲线
振动方程：xAsi nt ()
2020/11/29
16
振动方程
中各量含义：
xAsi nt ()
1. A叫简谐运动的振幅.表示简谐运动的 强弱.
2. 叫圆频率.表示简谐运动的快慢. 它与频率的关系： =2f
2020/11/29
6
3.频率
• ①做简谐运动的物体，在单位时间 内完成全振动的次数叫频率。它也 用来反映物体的振动快慢。
• ②频率的单位是 赫兹(Hz)，常用符 号为 f
2020/11/29
7
二、振幅与位移，周期与频率的关系
振幅与位移一样吗？
1.振幅与位移
①振幅反映振动强弱，位移反映位置变化。
2020/11/29
20
五、振子的路程和位移
①无论从什么位置开始计时，物体在一个周期内
通过的路程均为4A。
②无论从什么位置开始计时，物体在1/2个周期内
通过的路程均为2A。
③物体在任意1/4周期内通过的路程不一定等于A，
可2能020/大11/2于9 A，可能小于A，当然也可能等于A。
21
简谐运动中阵子的位移、速度、加速 度的变化具有周期性
(1)同相：相位差为 零，一般地为 =2n (n=0,1,2,……)
(2)反相：相位差为 ，一般地为
=(2n+1)
(n=0,1,2,……)
2020/11/29
14
思考与讨论
1、一个物体运动时其相位变化多少就意味着完成 了一次全振动?
相位每增加2π就意味着发生了一次全振动
2、甲和乙两个简谐运动的相差为 ，意味着什么? 2
2020/11/29
12
实际上经常用到的是两个相同频率的简 谐运动的相位差，简称相差
t 2 t 1 2 1
同相：频率相同、初相相同(即相差为0） 的两个振子振动步调完全相同
反相：频率相同、相差为π的两个振子 振动步调完全相反
2020/11/29
13
(2- 1)叫相位差(两个具有相同频率的 简谐运动的初相之差).对频率相同的两个 简谐运动有确定的相位差．
做简谐运动的物体在任意1/2个周期内通过的路程是多少？ ②无论从什么位置开始计时，物体在1/2个周期内 通过的路程均为2A
做简谐运动的物体在任意1/4个周期内通过的路程是多少？
2020/11/29
19
五、振子的路程和位移
①无论从什么位置开始计时，物体在一个周期内 通过的路程均为4A ②无论从什么位置开始计时，物体在1/2个周期 内通过的路程均为2A
• 位移：振动物体的位移式物体相对于平衡位置的 位移，它总是以平衡位置为始点，方向由平衡位 置指向物体所在的位置，位移的大小等于这两个 位置之间的距离，物体经平衡位置时位移方向发 生改变
• 速度:简谐运动是变加速运动，物体经平衡位置时 速度最大，物体在最大位移处时速度为零，且物 体的速度在最大位移处改变方向
• 加速度：物体处在最大位移处时加速度最大，物
体处在平衡位置时加速度最小（为零），物体经
平衡位置时，加速度方向发生改变。
2020/11/29
22
物理量
位移（X）
加速度（a）
速度（V）
方向 大小 方向 大小 方向 大小
B’
O
B
变化过程
BO
向右 减小
向左 减小 向左 增大
O B’ B’ O O B
向左 向左 向右
• “不怕太阳晒，也不怕那风雨狂，只怕先生骂我 笨，没有学问无颜见爹娘 ……”
• “太阳当空照，花儿对我笑，小鸟说早早早……”
2020/11/29
4
一、振幅，周期和频率
1.振幅 ①振动物体离开平衡位置的最大位移叫振幅。 振幅能够反映什么？
②振幅用来反映振动物体振动的强弱（系统蕴涵的能量） ③振幅的单位是m，符号是A。