投票博弈

基于博弈论分析的数字创意平台投票机制
曾美玲;王滔滔;吴国声
【期刊名称】《信息工程期刊:中英文版》
【年(卷),期】2022(10)1
【摘要】数字技术和互联网技术的新进展推动数字创意产业进入了新时代,数字创意产业也面临着一系列新的挑战。

区块链作为一项颠覆性的技术,其技术特点能够给数字创意产业带来很多新的应用,尤其是区块链中的一种非同质化代币(Non-Fungible Token,NFT)技术融入到数字创意产业中能够给该产业带来新的变革。

然而,数字创意作品平台系统因“零门槛”进入而面临低质量作品泛滥的问题。

本文提出在作品被平台收纳之前应引入投票机制来解决该问题。

我们首先为平台中的创作者建立基于博弈论的经济模型,并对比分析均分机制、比例机制以及投票机制在达到对称均衡时创作者产出作品质量的情况。

通过博弈论理论分析与计算机仿真实验表明,在引入投票机制之后,系统可以通过改变总奖励的方式有效激励创作者上传更高质量的作品到平台中,从而自动过滤低质量作品。

【总页数】12页(P1-12)
【作者】曾美玲;王滔滔;吴国声
【作者单位】云链网科技(广东)有限公司;深圳大学
【正文语种】中文
【中图分类】TP3
【相关文献】
1.基于开放平台的数字版权授权机制研究——以百度文库数字版权开放平台为例
2.基于产业公共技术服务平台的创客空间建设*--以深圳市数字创意公共技术服务平台为例
3.基于博弈论的中药材网上交易平台采购质量分析
4.基于博弈论的P2P网贷平台监管分析——兼论帕累托最优路径选择
5.基于博弈论的档案数字化项目监理运行机制研究
因版权原因，仅展示原文概要，查看原文内容请购买。

博弈论学习笔记（七）纳什均衡伯川德模型与选民投票古诺模型复习在古诺模型中，多少如我们所预料的，事情很⾃然的处于极端情况之间，即⾏业产量在某种程度上是介于在垄断和完全竞争两种情况之间的。

它⽐在垄断下的价格低，⽐在完全竞争下的价格⾼；⾏业利润⽐垄断下的利润低，⽐完全竞争时的利润⾼。

如果想要得到不完全竞争的局⾯，他么他就在垄断与完全竞争之间。

但是在另外⼀种情况下能够得到⼀种完全拨通的模型 -- 伯川德竞争（Bertrand competition）。

伯川德模型的饮料案例同样是卖饮料，但是这次的的策略是每单位商品的价格p,我们设：有两个参与者1和2，他们分别卖可⼝可乐和百事可乐。

参与者i的出价策略为p i，i=1，2。

编辑成本为c。

对于参与者1，对于不同的出价p1，对应的销量q1为：当p1<p2，q1=1-p1当p1>p2，q1=0当p1=p2，q1=(1-p1)/2这种情况下p1=p2=c为纳什均衡。

如果参与者1选择某个⼤于c的价格p1=c+3*ε，参与者2就会选择⼀个较⼩的价格，如p2c+2*ε，从⽽迫使价格趋向于两者都为编辑价格c，达到纳什均衡。

选民投票n个⼈的政治⽴场平均分布在⼀条直线上，其中越左边的⼈的政治⽴场⽉偏向于左翼，越右边的⼈的政治⽴场⽉偏向于右翼。

他们可以选择竞选总统或者作为选民。

如果他们作为选民，那么他们的选票将会投给离他⾃⼰政治⽴场最近的⼀个参选者。

如果有位置⼀样的则平分。

举个例⼦，如果现在在x位置有⼀个⼈如果x位置的⼈参选并且获胜，他将得到收益b-c（这⾥假设b=2*c，c是竞选的成本）如果x位置的⼈参选y位置的⼈获胜，他将得到收益-c-|x-y| 若果x位置的⼈没有竞选总统，⽽离他最近的y位置的⼈赢得了竞选，他将得到的收益为-|x-y|假设n为奇数，如果现在每个位置平均只有⼀个⼈，那么：只有中间那⼀个⼈竞选是纳什均衡，因为当他竞选时不管是他左边有个⼈想站出来竞选还是他右边有个⼈想站出来竞选都不会成功。

前言：投票博弈（一）投票博弈知识点：【定义1】：设投票博弈中，参加投票人的集合为N=｛1,2,……,n｝。

N的一个子集S称为一个联盟。

【定义2】：设投票博弈中, 若对某一个联盟S满足：（1）投票人i 在S中；（2）S中的投票人一致同意，则提出的议案通过；且S \｛i｝中的投票人一致同意，则提出的议案不能通过。

则该联盟S称为投票人i 的一个摆盟。

【定义3】：用θi表示第i个投票人的摆盟数，则记βi= θi /（θ1+θ2+……+θn）i=1，2,…,n β=(β1 称为Banzhaf势指标。

一般情况下，可用-------------------------------------------------------例1：一个董事会有4位董事，其中董事长有3票，副董事长有2票，剩余2名董事各有1票，进行投票表决。

表决的规则是：超过半数票，讨论的提案通过。

问：1）副董事长的权力和1个董事的权力有多大的差异？2）若表决的规则是：超过2/3票，讨论的提案通过。

副董事长的权力和1个董事的权力有多大的差异？1）解：投票人集合：N=｛1，2，3，4｝。

设Si为投票人i的摆盟，i =1,2,3,4。

S 1：｛1,2｝、｛1,3｝、｛1,4｝、｛1,2,3｝、｛1,2,4｝、｛1,3,4｝S 2 ：｛2,1｝、｛2,3,4｝S 3 ：｛3,1｝、｛3,2,4｝S 4 ：｛4,1｝、｛4,2,3｝摆盟数为：θ1 = 6, θ2 = 2, θ3 = 2, θ4 = 2.势指标为：β1 = 1/2, β2 = β3 = β4 = 1/6（即副董事长与董事权力无差异）。

2）解：若表决的规则改为：达到或超过2/3时，提出的议案通过。

解：投票人集合：N=｛1,2,3,4｝。

设Si为投票人i的摆盟，i=1,2,3,4。

S1：｛1,2｝,｛1,2,3｝,｛1,2,4｝,｛1,3,4｝,｛1,2,3,4｝S2：｛2,1｝、｛2,1,3｝、｛2,1,4｝S3：｛3,1,4｝S4：｛4,1,3｝摆盟数为：θ1 = 5, θ2 = 3, θ3 = 1, θ4 = 1.势指标为：β1 = 5/10，β2 = 3/10, β3= β4 = 1/10例2：一个董事会由4位股东组成，每位股东依次拥有股份为：40%，30%，20%，10%。

投票博弈：美国大选重新计票检视
万倩倩
【期刊名称】《重庆行政(公共论坛)》
【年(卷),期】2017(018)004
【总页数】2页(P46-47)
【作者】万倩倩
【作者单位】中共重庆市委党校研究生部
【正文语种】中文
【相关文献】
1.从美国总统大选看电子投票技术的新发展 [J], 张珂
2.两党博弈媒体媒体倾力助阵——2012美国总统大选冲刺阶段各类媒体评析 [J], 崔银河;柯安德
3.黑客干预美国大选：大国博弈与国际网络安全冲突 [J], 鲁传颖
4.新媒体时代精英群体与大众群体话语博弈r——以美国大选为例 [J], 晁辛宁
5.干部推荐投票中多主体博弈与计票规则改进分析 [J], 王凌峰;胡卫敏
因版权原因，仅展示原文概要，查看原文内容请购买。

投票悖论的名词解释在现代民主制度中，投票是一种重要的决策方式。

人们通过投票选择代表，支持或反对特定的议题，影响政府政策的制定和执行。

然而，在投票过程中，存在着一些看似矛盾和悖论的现象，这就是所谓的投票悖论。

投票悖论是指在特定条件下，投票结果可能会引发矛盾或错误的结论。

具体来说，投票悖论依赖于个人偏好的聚合问题。

简单来说，当个人对多个选择或候选人进行排序时，将这些个人偏好相互整合可能会导致不稳定、混乱或矛盾的结果。

这一现象最早由法国数学家和政治学家孔度（Condorcet）在18世纪末提出。

孔度发现，当投票参与者人数较多、选择数量较多时，个人的偏好往往无法稳定地在集体决策中得到准确体现。

投票悖论有许多具体的例子，其中著名的有孔度悖论、阿罗悖论和德林格悖论。

这些悖论展示了在不同投票规则下，投票结果可能会产生不同效果，甚至引发逻辑上矛盾的结论。

孔度悖论的一个例子是当有超过两个候选人时，个人偏好的汇总可能会导致循环优势。

也就是说，在一个三人选举中，如果每个选民都按照 A>B>C 的顺序进行排序，那么根据赢得多数票的标准，A可能赢得第一轮投票。

然而，当以同样的方式对比 B 和 C 时，B 可能会赢得第一轮投票。

最后，对比 C 和 A 时，C 也可能赢得第一轮。

这种循环优势导致了投票结果的不稳定性。

阿罗悖论关注的是个人偏好与集体偏好之间的矛盾。

当个体的偏好只考虑到部分因素时，对于整个群体来说，可能会出现倒数效应。

倒数效应是指当某一候选人的排名在个体中上升时，整个群体对该候选人的排名反而下降。

德林格悖论与传统的投票规则相关。

传统的投票规则通常使用排名制，允许选民以某种顺序来排列候选人。

然而，德林格悖论表明，这种投票方式并不一定能够准确地反映选民的真实偏好。

简单而言，个人的偏好可能会受到候选人的数量和排名方式的影响，从而导致不同的投票结果。

投票悖论的存在提醒着我们，在设计和运用投票制度时需要谨慎考虑。

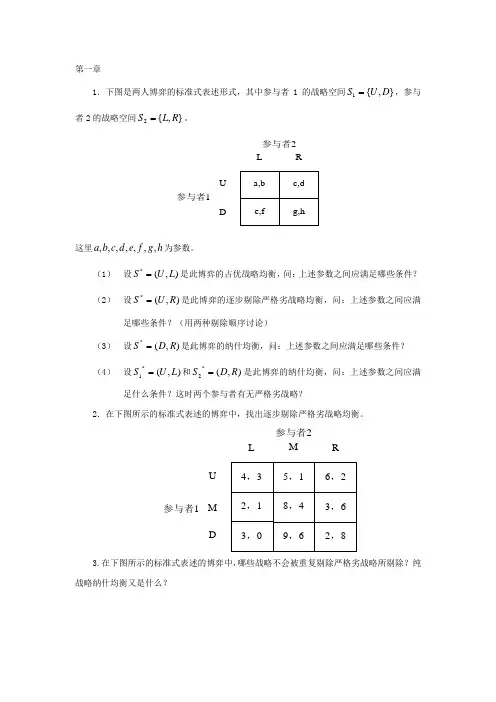
第一章1．下图是两人博弈的标准式表述形式，其中参与者1的战略空间},{1D U S =，参与者2的战略空间},{2R L S =。

参与者2 参与者1LR D U这里h g f e d c b a ,,,,,,,为参数。

（1） 设),(*L U S =是此博弈的占优战略均衡，问：上述参数之间应满足哪些条件？（2） 设),(*R U S =是此博弈的逐步剔除严格劣战略均衡，问：上述参数之间应满足哪些条件？（用两种剔除顺序讨论）（3） 设),(*R D S =是此博弈的纳什均衡，问：上述参数之间应满足哪些条件？（4） 设),(*1L U S =和),(*2R D S =是此博弈的纳什均衡，问：上述参数之间应满足什么条件？这时两个参与者有无严格劣战略？2．在下图所示的标准式表述的博弈中，找出逐步剔除严格劣战略均衡。

参与者2 参与者1 LM MUD R 3.在下图所示的标准式表述的博弈中，哪些战略不会被重复剔除严格劣战略所剔除？纯战略纳什均衡又是什么？参与者2 参与者1 LC MTB R 4.下图所示的标准式表述的三人博弈中，参与者1的战略空间},{1D U S =，参与者2的战略空间},{2R L S =，参与者3的战略空间},,{3C B A S=。

参与者1选择两行中的某一行，参与者2选择两列中的某一列，参与者3选择三个矩阵的某矩阵。

找出此博弈的纯战略纳什均衡。

LR D UA L RB L R C5.(投票博弈)设有三个参与者)3,2,1(=i 要在三个项目（A,B 和C ）中投票选出一个。

三个参与者同时投票，不允许弃权。

因此，三个参与者的战略空间为)3,2,1}(,,{==i C B A S i 。

得票最多的项目被选中。

如果没有任何项目得到多票数，那么项目A 就被选中。

某个项目被选中后三个参与者的收益函数如下：2)()()(321===C u B u A u1)()()(321===A u C u A u0)()()(321===B u A u C u（1） 写出此博弈的标准式表达；（2） 求出此博弈的纯战略纳什均衡。

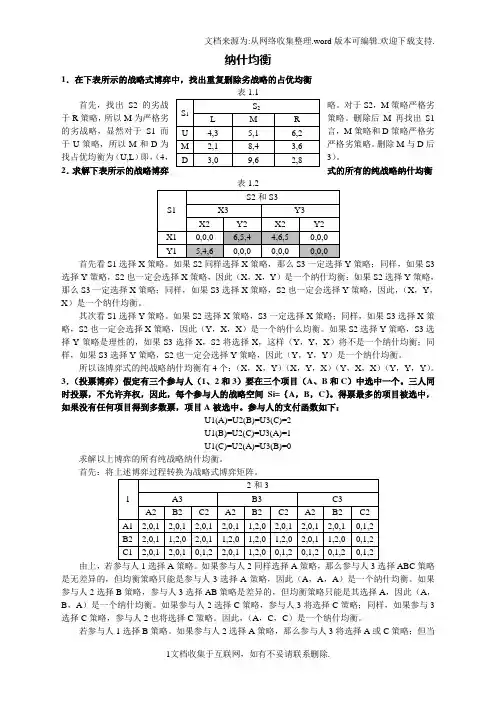
纳什均衡1．在下表所示的战略式博弈中，找出重复删除劣战略的占优均衡表1.1于R策略，所以M为严格劣策略。

删除后M再找出S1的劣战略，显然对于S1而言，M策略和D策略严格劣于U策略，所以M和D为严格劣策略。

删除M与D后找占优均衡为（U,L）即，（4，3）。

2．求解下表所示的战略博弈式的所有的纯战略纳什均衡表1.2首先看S1选择X策略。

如果S2同样选择X策略，那么S3一定选择Y策略；同样，如果S3选择Y策略，S2也一定会选择X策略，因此（X，X，Y）是一个纳什均衡；如果S2选择Y策略，那么S3一定选择X策略；同样，如果S3选择X策略，S2也一定会选择Y策略，因此，（X，Y，X）是一个纳什均衡。

其次看S1选择Y策略。

如果S2选择X策略，S3一定选择X策略；同样，如果S3选择X策略，S2也一定会选择X策略，因此（Y，X，X）是一个纳什么均衡。

如果S2选择Y策略，S3选择Y策略是理性的，如果S3选择X，S2将选择X，这样（Y，Y，X）将不是一个纳什均衡；同样，如果S3选择Y策略，S2也一定会选择Y策略，因此（Y，Y，Y）是一个纳什均衡。

所以该博弈式的纯战略纳什均衡有4个：（X，X，Y）（X，Y，X）（Y，X，X）（Y，Y，Y）。

3．（投票博弈）假定有三个参与人（1、2和3）要在三个项目（A、B和C）中选中一个。

三人同时投票，不允许弃权，因此，每个参与人的战略空间Si=｛A，B，C｝。

得票最多的项目被选中，如果没有任何项目得到多数票，项目A被选中。

参与人的支付函数如下：U1(A)=U2(B)=U3(C)=2U1(B)=U2(C)=U3(A)=1U1(C)=U2(A)=U3(B)=0求解以上博弈的所有纯战略纳什均衡。

由上，若参与人1选择A策略。

如果参与人2同样选择A策略，那么参与人3选择ABC策略是无差异的，但均衡策略只能是参与人3选择A策略，因此（A，A，A）是一个纳什均衡。

如果参与人2选择B策略，参与人3选择AB策略是差异的，但均衡策略只能是其选择A，因此（A，B，A）是一个纳什均衡。

【关键字】均衡纳什均衡1．在下表所示的战略式博弈中，找出重复删除劣战略的占优均衡首先，找出S2的劣战略。

对于S2，M 策略严格劣于R 策略，所以M 为严格劣策略。

删除后M 再找出S1的劣战略，显然对于S1而言，M 策略和D 策略严格劣于U 策略，所以M 和D 为严格劣策略。

删除M 与D 后找占优均衡为（U,L ）即，（4，3）。

2．求解下表所示的战略博弈式的所有的纯战略纳什均衡首先看S1选择X 策略。

如果S2同样选择X 策略，那么S3一定选择Y 策略；同样，如果S3选择Y 策略，S2也一定会选择X 策略，因此（X ，X ，Y ）是一个纳什均衡；如果S2选择Y 策略，那么S3一定选择X 策略；同样，如果S3选择X 策略，S2也一定会选择Y 策略，因此，（X ，Y ，X ）是一个纳什均衡。

其次看S1选择Y 策略。

如果S2选择X 策略，S3一定选择X 策略；同样，如果S3选择X 策略，S2也一定会选择X 策略，因此（Y ，X ，X ）是一个纳什么均衡。

如果S2选择Y 策略，S3选择Y 策略是理性的，如果S3选择X ，S2将选择X ，这样（Y ，Y ，X ）将不是一个纳什均衡；同样，如果S3选择Y 策略，S2也一定会选择Y 策略，因此（Y ，Y ，Y ）是一个纳什均衡。

所以该博弈式的纯战略纳什均衡有4个：（X ，X ，Y ）（X ，Y ，X ）（Y ，X ，X ）（Y ，Y ，Y ）。

3．（投票博弈）假定有三个参与人（1、2和3）要在三个项目（A 、B 和C ）中选中一个。

三人同时投票，不允许弃权，因此，每个参与人的战略空间Si=｛A ，B ，C ｝。

得票最多的项目被选中，如果没有任何项目得到多数票，项目A 被选中。

参与人的支付函数如下：U1(A)=U2(B)=U3(C)=2U1(B)=U2(C)=U3(A)=1U1(C)=U2(A)=U3(B)=0求解以上博弈的所有纯战略纳什均衡。

由上，ABC 策略是无差异的，但均衡策略只能是参与人3选择A 策略，因此（A ，A ，A ）是一个纳什均衡。

政党政治第一节政党基本理论一、政党的概念1. 政党的产生与发展：17世纪的英国（辉格党和托利党）——19世纪选举权的扩大导致政党政治的出现——20世纪50年代政党普遍增多——60、70年代一度回落——90年代民主化浪潮下重新蓬勃发展2. 政党的定义：①西方政治学的基本观点：政党是为谋取权力和控制政府而形成的组织。

政党是通过赢得大选的方式来影响政府为目标的组织。

——罗斯金②马克思主义政治学的基本观点：政党是阶级利益的代表。

政党本质上是特定阶级利益的集中代表者，是特定阶级政治力量中的领导力量，是由各阶级的政治中坚分子为了夺取或巩固国家政治权力而组成的政治组织。

——王浦劬二、政党的特征1.政党是特殊的政治历史现象——政党为什么在近代才开始出现物质条件：现代交通、通讯等技术手段的发展制度条件：民主共和制度2.政党由阶级中一部分先进人物组成萨托利：政党不是派系；整体中的部分；表达渠道。

3.政党的组织性纪律性——政党的社会动员能力强弱取决于其组织性和纪律性。

4.政党都有自己的政治纲领——通过政治纲领来作为行动目标，获取支持。

5.政党与政权密不可分——夺取、巩固或影响政权与政府活动。

三、政党的分类四、政党的功能1.争取和影响群众：社会化和动员2.集中阶级意志：代表、制定目标、利益表达和聚合3.行使国家权力：组织政府4.培养领导干部：培养和录用政治精英第二节资本主义政党及政党制度一、资产阶级政党的产生原因1. 价值观念：自由、平等价值的深入人心2. 社会制度：宪政、代议制、普选制的发展3. 政治社会化: 传统人际关系的衰落和政治社会化途径的转变二、资产阶级政党的基本特征1.超阶级性：弱化意识形态和阶级立场（选举中间人定理）2.围绕议会和选举开展活动：获取选票的多少决定政党的兴衰存亡。

3.组织上的两极化倾向：上紧下松4.党内派系斗争合法化、公开化5.奉行公平竞争原则三、资产阶级政党在国家政权中的作用1.资产阶级民主政治的基石：西方民主政治三大支柱：选举制、议会制、政党制度2.协调民主制度的运作：民主与分权的低效率通过政党可以适当弥补3.西方政治系统的自我调节机制：保证面对不断发展的社会、政治、经济中的问题而不断调适与变革四、资本主义国家政党制度迪维尔热的政党分类：（标准：竞取权力的政党数目）一党制、两党制、多党制（三个政党以上）①概念：国家政权被国内唯一合法的政党所垄断，在法律上或在事实上都不允许其他政党存在的一种政党制度。

投票博弈：美国大选重新计票检视作者：万倩倩来源：《重庆行政》2017年第02期美国大选日，特朗普以304张选举人票（但特朗普的选民票却比希拉里少200多万），赢得本次竞选。

但绿党候选人吉尔以“计票有问题”，申请在威斯康辛、宾夕法尼亚和密歇根等三个州选票重新统计。

由此，拉开美国历史上第三大选重新计票的序幕。

这种以民选票少于对手而获胜的现象，政治学家称为“错误的人当选”。

因此，不妨对美国大选重新计票事件进行检视。

一、美国历史大选投票的经典博弈美国大选由于其特殊的选举人团制度（赢家通吃原则），使得候选人可能赢得选民票却输掉选举人票，导致大选失败。

美国大选历史上曾出现五次“以少胜多”情况，且有三次要求重新计票情况。

（一）美国的选举人团制度从1787年美国《宪法》成文起，就规定了总统选举施行选举人团制度，至今已200多年历史。

选举人团制度：一是各州选出的选举人团间接选举美国总统；二是各州选民选出的选举人拥有的选举人票数同该州在国会拥有的参议院和众议院的议员人数相等。

在参议院是每个州2个名额，在众议院则按各州人口比例分配；三是除了缅因和纳布拉斯加两个州是按选民票得票比例分配选举人票外，其余48个州和华盛顿特区均采用“赢家通吃”制度。

即获得相对较多选民票的候选人将得到本州的全部选举人票；四是候選人获得270张选举人票（全美50个州和华盛顿特区总共538票的一半以上）便可当选；五是当没有候选人获得半数以上的选举人票时，由国会众议院从得票排名前三的候选人中选出总统。

（二）五次以少胜多的大选美国总统选举中曾出现过五次“以少胜多”情况（候选人获得较少的选民票，却拥有较多的选举人票，最终赢得选举）：1824年，昆西·亚当斯以30.5%的选民票，战胜拥有43.1%选民票的杰克逊；1876年，海斯以48%的选民票，战胜拥有51%选民票的提尔登，多近25万张选民票；1888年，哈利森以47.9%的选民票，战胜拥有48.6%选民票的克利夫兰；2000年，布什以47.87%的选民票，战胜拥有48.38%选民票的戈尔。