数学建模机器人避障问题

v1.0 可编辑可修改机器人避障问题的解题分析摘要：本文对2012年全国大学生数学建模竞赛D题机器人避障问题进行了全面分析，对最短路的设计进行了理论分析和证明，建立了机器人避障最短路径的几何模型，对最短时间路径问题通过建立非线性规划模型，有效地解决了转弯半径、圆弧圆心位置和行走时间等问题。

关键词：机器人避障；最短路径；Dijkstra算法；几何模型；非线性规划模型1 引言随着科学技术的进步和计算机技术的发展，机器人的应用越来越广泛，在机器人的应用中如何使机器人在其工作范围内为完成一项特定的任务寻找一条安全高效的行走路径，是人工智能领域的一个重要问题。

本文主要针对在一个场景中的各种静态障碍物，研究机器人绕过障碍物到达指定目的地的最短路径问题和最短时间问题。

本文以2012年“高教社”杯全国大学生数学建模竞赛D题“机器人避障问题”为例进行研究。

假设机器人的工作范围为800×800的平面正方形区域（如图1），其中有12个不同形状的静态障碍物，障碍物的数学描述（如表1）：图1 800×800平面场景图表1在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动，机器人不能与障碍物发生碰撞，障碍物外指定一点为机器人要到达的目标点。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为50=v 个单位/秒。

机器人转弯时，最大转弯速度为21.0100e1)(ρρ-+==v v v （ρ是转弯半径）。

如果超过该速度，机器人将发生侧翻，无法完成行走。

场景图中有4个目标点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，下面我们将研究机器人从O(0, 0)出发，求O→A、O→B、O→C和O→A→B→C→O的最短路径，以及机器人从O(0, 0)出发，到达A的最短时间路径问题。

2012高教社杯全国大学生数学建模竞赛D题评阅要点[说明]本要点仅供参考，各赛区评阅组应根据对题目的理解及学生的解答，自主地进行评阅。

问题常见于计算机图形处理和机器人自动行走，其中二维和三维避障问题是热点课题。

固定场景中的避障是其中较简单的情形，不涉及障碍物的移动和障碍物的识别。

本问题的数学模型和求解算法份量基本相当。

1．预处理：将原始障碍物作适当扩大，确保不发生碰撞。

在合理的假设下，要求预处理步骤清晰，说明适当，明确给出最后的处理结果。

2. 数学模型：必须明确建立路程最短和时间最少的优化模型，要给出明确的决策变量、目标函数和
约束条件，表述准确全面。

3. 求解方法：机器人路径规划求解方法较多，尽量选择合适的求解方法和相应的算法，给出求解方
法的思想，求解算法的步骤或流程图，并给出图形的预处理过程和描述。

4. 结果与分析：要有明确的数值结果和路线图，表达简明、清晰。

最优路径应由直线段与圆弧光滑
连接而成。

例如，第一问的圆弧半径为10，第二问的圆弧半径需通过优化模型计算得到。

例如，到B点距离最短的最优路径可参见图1，到A点时间最短的最优路径可参见图2。

5. 深入分析：本问题有较大的发挥空间，参赛者利用参考文献作深入分析时，可考虑适当加分。

（1）讨论不同算法对2种最优结果的影响；
（2）适当考虑直线行走与转弯之间时间延迟的影响；
（3）适当扩充，讨论障碍物变形或不规则障碍物对最优结果的影响等；
（4）适当扩充，定性讨论障碍物的适当移动或目标点的适当移动对结果的影响，或者定性讨论三维空间的情况等。

图1 图2。

机器人避障问题摘要本文主要运用直线逼近法等规律来解决机器人避障问题.对于问题一：要求最短路径运用直线逼近法证得圆弧角三角形定理，得出结论：若一大圆弧角三角形完全包括另一小圆弧角三角形，则该三角形曲线周长必大于小的三角形周长.那么可知机器人在曲线过弯时，选择最小半径可满足路径最短，即为10个单位半径，通过观察可得可能的所有曲线，通过仅考虑直线段的大致筛选选出总长较小、长度相近（之差小于100）的曲线，然后利用平面几何知识对相关切点，进而求出各直线、曲线的长度，求和可得最段路线.对于问题二：通过对机器人过弯规律21.0100e 1)(ρρ-+==v v v 的分析可知，当过弯半径13ρ=时，机器人速度达最大速度为50=v 个单位/秒，再大就无变化了，那么可分两种情况考虑：1）当13ρ>时，过弯速度无变化，但由圆弧角三角形定理可知，此时随着ρ的不断变大，其路线总长不断变大，这时ρ越小O A →所用时间最短；2）当13ρ≤时，统计计算ρ分别为10、11、12、13时，过弯速度v 也不断变化，计算所用时间发现随ρ不断变大，O A →所用时间越短，此时当13ρ=时，时间最短.综合上述可知：当13ρ=时，时间最短.关键词：质点机器人 安全范围 直线逼近法 圆弧角三角形定理 10单位半径1 问题重述在一个800×800的平面场景中，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动，其中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，物的距离至少超过10个单位）.规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径.机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位.为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位.机器人直线行走的最大速度为50=v 个单位/秒.机器人转弯时，最大转弯速度为2100.110()(1e)v v v ρρ--==+，其中ρ是转弯半径.如果超过该速度，机器人将发生侧翻，无法完成行走.下面建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型.对场景图中4个点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，具体计算：(1) 机器人从O(0, 0)出发，O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径. (2) 机器人从O (0, 0)出发，到达A 的最短时间路径.2 问题分析2.1问题一：该问题要求路径最短，即不要求速度与时间，则可认为以最小半径10的圆过弯.如图2.1所示：由圆弧角三角形定理（简单证明见模型准备5.3）可知过弯时，只有采用10单位半径过弯时，才会使得过弯路径最短，因此解决问题一的过弯拐角问题均采用10单位半径过弯路径. 2.2问题二：由于O→A 过程中，机器人至少要经过一次转弯；因为转弯时的速度一般小于直线行走的最大速度，又由分析指出转弯次数越多，转弯路径越远，转弯所花费的时间也越长.所以可以确定有且只有一次转弯时才存在最短时间路径.就仅考虑只经过一次转弯的情形.3 模型假设1）假设机器人可准确执行运动轨道，无任何偏差；2）假设机器人为一可运动的质点，即质点机器人不考虑其外形尺寸； 3）假设机器人的行进速度可瞬时加减变化，不受条件限制；4）假设机器人可到达边界线而不会发生碰撞，即对边界线不再加10个单位.4 符号说明hij D ： 机器人的行走路径上各切点，h 表示路径目的地（A 、B 、C ），i 表示到达h 机器人行走路线的第(1,2,3,)i i = 种方案，j 表示机器人在该路线上所经过的第(1,2,3,)i i = 个点；hij L : 机器人的行走路径上的线段长或弧长，h 、i 、j 同上定义；ij D ：机器人的行走路径上的障碍物的顶点，i 、j 同上定义；`hj D ：机器人在O A B C O →→→→环道中的各线切点h 、j 同上定义5 模型准备5.1建立机器人运动坐标系：以O 为原点，两对应坐标轴，水平方向为X 轴，垂直方向为Y 轴5.2建立机器人可安全运动到达的区域图：由于保持安全距离10个单位，则机器人的实际可到达到区域应由各障碍物的外延10个单位的区域组成如图所示图5.2.1实线外的空白部分.5.3圆弧角三角形定理：定义1：平面内若两不平行直线所夹的角被一同时与这两条直线相切的圆弧段取代而形成的角，叫做圆弧角.如图5.3.2，称为凸圆弧角（本文主要讨论）；如图 5.3.3，称为凹圆弧角.定义2：由有一内角为凸圆弧角的三角形为圆弧角三角形.圆弧角三角形定理：圆弧角`DHD ∠在直线`DD 及上方范围完全包含圆弧角`DGD ∠（即圆弧角DGD ’各边均在圆弧角`DHD ∠的边与线段DD ’所构成的封闭区间内，如图5.3.1所示）时，则有曲线段`DGD 的长度恒小于曲线段`DHD 成立.证明：如图 5.3.1，过圆弧 'EGE的一个端点E 作该圆弧在该点的切线的垂线交曲线DH 于点F ，同样过圆弧 'EGE的另一个端点'E 也作相应的垂线交曲线'D H 于点'F ，两条直线的交点O 显然为圆弧 'EGE 所在圆的圆心. （1）,EF DE ⊥ 90DEF ∴∠=︒ ；,DF DE ∴> 曲线段DF DF ≥， ∴曲线段DF DE >.（2）'''',E F D E ⊥ '''90D E F ∴∠=︒；'''',D F D E ∴> 曲线段''''D F D F ≥；∴曲线段''''D F D E >.（3）将''EFF E 分成n 等份（如图5.3.5），每部分（见图5.3.4）中，,(1,,)i i M N i n = 是 MN 与边界的交点.令i i M N 为i M ，i N 两点间直线长度，''i i M N 为`i A ,`i E 两点间直线长度，则圆弧 MN 长度=1lim ni i n i M N →∞=∑，曲线`AE 长度=''1lim ni in i M N →∞=∑又容易证明，''(1,,)i i i i M N M N i n ≤= ，故有''11lim lim n ni i i i n n i i M N M N →∞→∞==≤∑∑ .因此，圆弧 MN长度≤曲线 ''M N 长度. 综合（1）（2）（3）的证明，得曲线段DF +曲线段''D F +曲线 ''M N 长度 > DE +''D E +圆弧 MN长度.结论得证. 6 模型建立与求解该问题要求路径最短，即不要求速度与时间，则可认为过弯半径允许以最小半径10，如图6.1所示.由圆弧角三角形定理可得：本论文问题一求路径最短可采用10单位过弯半径，即以半径为10个单位的圆弧过弯可满足两点避障过弯最短问题.6.1问题一的模型建立与求解：6.1.1：机器人从O(0, 0)出发，O A →的最短路径. 由圆弧角三角形定理可得：采用10单位半径过弯路径最短，解决过弯避障拐角问题采用10单位半径过弯路径.已知机器人所走路线为直线或圆弧，那么通过实际规划可得如下四种避障行进方案：如图6.1.1首先对上述四条路线进行筛选：1）当机器人以一个连续圆弧过弯，即选择路 线二或路线四时,其中路线二：分别过点O A ，和障碍物5的切点23a D （72.74，216.88），则可得过该三点的圆的方程：225406140x y x y ++-=显然当0x =时，y 有不等的两个根，则该路线超出规定场地. 同理路线四的圆方程：22(73.98)(226.02)56558.350x y -+--= (Matlab 求解程序见程序01) 当0y =时，x 有不等的两个根，则该路线也超出规定场地.2）当机器人以直线—圆弧—直线的方式过弯，即有以10单位半径过弯模式的线路一和三：比较线路一与线路三：显然路线一的总长1111213a a a a L L L L =++，线路三的总长3313233a a a a L L L L =++. 解得13471.04498.44a a L L =>=则可知O→A 的最短路径为路线一总长为1471.04a L =，下表5.1.1为线路一的各点的详细参数，表6.1.2为各线的参数.表6.1.26.1.2机器人从O(0, 0)出发，O B →的最短路径由圆弧角三角形定理可得：采用10单位半径过弯路径最短： 通过观察可得如下四种较短的避障行进方案，如图6.1.2：由于方案较多，可预先进行粗略筛选：如图所示：大致统计长度仅包括直线段长度如下表6.1.2线的精确长度：设：11b OD 、1111b D D分别表示O 点到点11b D ，点11b D 到点11D 之间的向量；1111b D D 为11b D 、11D 两点之间的向量的模；()()(),hij hij x y 表示切点hij D 坐标；()()(),ij ij x y 记为障碍物顶点ij D 的坐标；b11L2220(b12)(b11)(b12)(b11)00b12-((x -x )+(y -y ))22=arccos()L ρρρ⨯b13L11(11)(00)(11)(00)(,)b b b OD x x y y =-- ()1 61(61)(00)(61)(00)(,)OD x x y y =--1111(11)(11)(11)(11)(,)b b b D D x x y y =--()2 1111110b b D D OD =()3 1111b D D r =()4联立方程()1()2()3()4解得11b D (50.14,30.64)由于点12b D ，13b D 分别是以点61D ，61D 为圆心r 为半径圆的外公切线切点，所以 由点到直线的距离公式得0ρ= ()50ρ=()6并且线段13126163b b D D D D =()7由于直线13126163b b D D D D 平行直线由斜率相等得(13)(13)(61)(63)(13)(13)(61)(63)b b b b x x x x y y y y --=-- ()8联立方程()5()6()7()8解得点12b D 的坐标(51.6795,305.547)13b D 的坐标(141.68,440.55)线路一和线路二的各段路线及总长分别如下表6.1.2,6.1.3同理可解得各点坐标如下表6.2.4→的最短路径为：O B6.1.3机器人从O(0, 0)出发，O C→的最短路径由圆弧角三角形定理可得：采用10单位半径过弯路径最短：通过观察可得如下避障行进方案，如图6.1.3由于该线路同样较复杂，可通过大致筛选，仅考虑其中的直线段长度.将通过障碍物1上边沿的线路称为上线路，通过下边沿的线路称为下线路1）考虑上线路中最短路径：上线路中如图6.1.3.1分两大段，上半段：线路A、B、C，下半段：线路D、E对上半段的线路进行只计算线段的粗筛选：计算统计可得三线路的粗选长度：如对下半段的线路进行只计算线段的粗筛选： 计算统计可得三线路的粗选长度：如表6.1.62）考虑下线路中最短路径： 如图图6.1.3.2对下线路的线路进行只计算线段的筛选：计算统计可得线路的长度：下表6.1.7为路线一的各段线路总长对于同一条路径上的两个相邻点(),i i x y 、()11,i i x y ++来说，如果这两点之间的路径为直线段时，用通式1L 计算；如果这两点之间的路径为弧线段时，可用通式2L 计算：1L 222011002-((-)(-))22=arccos()i i i i x x y y L ρρρ+++⨯下表6.2.8为路线二的各段线路总长下线路的两段线路对比得：线路一最短为：950.84综合上线段、下线段可得：线路一最短.各切点坐标如下表6.1.9表6.1.96.1.4机器人从O(0, 0)出发，O A B C O →→→→的最短路径 由圆弧角三角形定理可得：采用10单位半径过弯路径最短：6.1.4.1A B →的最短路径求解： 通过实际规划可得如下A B →的避障行进最短方案：如图6.1.4.16.1.4.2B C →的最短路径求解：通过实际规划可得如下A B →的避障行进最短方案：如图6.1.4.1对线路一、二进行大致选可得下表表6.1.10则可知路线一距离最近对于同一条路径上的两个相邻点(),iix y 、()11,i i x y ++来说，如果这两点之间的路径为直线段时，用通式1L 计算；如果这两点之间的路径为弧线段时，可用通式2L 计算：1L 222011002-((-)(-))22=arccos()i i i i x x y y L ρρρ+++⨯6.1.4.3线路经过A 、B 、C 的圆弧处理问题为使经过A 、B 、C 的圆弧路线最短，在A 与相邻切点的连线形成的夹角的平分线，以该角的平分线为基础，在该线上做与点A 相切的半径为10个单位的圆，则此时通过该构造圆与相邻圆弧的切线连接就产生了，进而保证了机器人的圆弧过弯和线路最短. 点A 的圆弧处理结果如图6.1.4.3则综上所述：求得各线短的最短路径，则可计算并统计出线段总长及各切点坐标如下表表6.1.116.2问题二的模型建立与求解：由于O→A 过程中，机器人至少要经过一次转弯；因为转弯时的速度一般小于直线行走的最大速度，又由分析指出转弯次数越多，转弯路径越远，转弯所花费的时间也越长.所以可以确定有且只有一次转弯时才存在最短时间路径.故以下就仅考虑只经过一次转弯的情形.机器人由起点到终点所用时间121255O AOQ Q AQ Q t v →=++，对于每种固定的转弯半径来说，转弯路径所在的圆的圆心与点(80,210)连线垂直平分该转弯路径所在的圆弧时，所得的总路径长度最短.如图6.2.1所示.对于已知条件中的最大转弯速度为21.0100e1)(ρρ-+==v v v ，其中ρ是转弯半径通过matlab 画出其图像，见程序02 如图6.2.2根据图6.1中所示，当1013R ≤<时，v 随R 增加而增加；当13R ≥时，v 已非常趋近于5单位/秒，此时可以看做v 不随R 增加而变化了.于是可以分两种情况解决本问题：1)当13R ≥时，由于O→A 整个过程的平均速度可以达到最大05v =单位/秒，以这样的速度沿最小的路径就可以使到达A 的时间最短.通过问题一中对机器人O→A 最短路径的分析，可知其最小时间路径应在OA 连线左上方区域；同时根据所建立并证明的圆弧角三角形定理可以知道，所得路径的转弯半径应为13个单位（如图6.2.3）1236.1392OQ =, 120.9077Q Q =,2223.1903Q A =,总长度： 1122++471.1296L OQ Q Q Q A == 总时间：1212471.135594.225595O AOQ Q A Q Q L t v →=++===（秒）2)当1013R ≤<时，图6.2取自原题目图中的一部分，其中(0,0)O ，2(80,210)O ，(300,300)A 点的坐标均已给出.1Q 、2Q 分别为OQ1和OQ2与1O 的切点，其中1O 又与2O 相切于3Q 点.假设半径R 已知，1O 、1Q 、2Q 、3Q 的坐标分别为00(,)x y 、11(,)x y 、22(,)x y 、33(,)x y ，则可列出如下方程组：2221010()()x x y y R -+-= 2222020()()x x y y R -+-= 2223030()()x x y y R -+-= 22233(80)(210)10x y -+-=21302130()()()()0x x x x y y y y --+--=310302108080y y y x x --=-- 110110()()0x x x y y y ⨯-+⨯-=202202()(300)()(300)0x x x y y y --+--=分别取R =10，11，12，13并解方程组可以得到总时间t 随转弯半径R 变化的数据，根据弧长公式得12Q Q AR =, A = 最终计算数据如下表：6.2.1最终会趋于94.22秒.因此，可以确定出最短时间路径.经过以上两种情况的讨论，可得最短时间路径， 具体坐标信息见表6.2.27 模型的评价与推广7.1优点：1)该模型采用较准确的及计算方法，数据精度高，可信度高. 2)该模型定义了新的几何名词与定理.具有一定的创新性. 3)利用估算法减少了计算量. 7.2缺点：程序利用率和执行率较低，计算量较大. 7.3应用与推广：自动控制技术 智能机器人技术 避障快速救援项目8参考文献[1]姜启源谢金星，数学建模，北京：高等教育出版社，2003[2]薛毅，数学建模基础，北京：北京工业大学出版社，2004[3]杨启帆方道元，数学建模，浙江，浙江大学出版社，19999附录程序01%三点确定圆方程%三点坐标x1=input('请输入x1=');y1=input('请输入y1=');x2=input('请输入x2=');y2=input('请输入y2=');x3=input('请输入x3=');y3=input('请输入y3=');if((y1==y2)&(y2==y3))disp('三点不构成圆!');elseif((y1~=y2)&(y2~=y3))k1=(x2-x1)/(y2-y1);k2=(x3-x2)/(y3-y2);endif(k1==k2)disp('三点不构成圆!');enda=2*(x2-x1);b=2*(y2-y1);c=x2*x2+y2*y2-x1*x1-y1*y1;d=2*(x3-x2);e=2*(y3-y2);f=x3*x3+y3*y3-x2*x2-y2*y2;disp('圆心为::');x=(b*f-e*c)/(b*d-e*a)y=(d*c-a*f)/(b*d-e*a)disp('半径为::');r=sqrt((x-x1)*(x-x1)+(y-y1)*(y-y1))利用参考文献：/thread-790618-1-1.html/求助已知3点怎么用MATLAB编程求圆的方程/参考程序程序02function plot_v_rr=0:0.5:20;v=5./(1+exp(10-0.1*r.^2));plot(r,v)grid on。

机器人避障问题摘要：当今科学技术日益发达，高科技产品尤其是机器人在我们日常生活中运用的越来越广泛，它能够代替人类完成许许多多的工作，但如何能让机器人自动化的完成人类交给的任务成为设计机器人的关键。

我们做此题就是为了更好的利用机器人为我们提供方便，提高生活质量，若机器人程序设计不当不仅不会给人类带来方便，还很有可能给我们的生活带来更多的麻烦。

本题中提出了如何让机器人能够自动识别障碍物，保证机器人能够在合理区域行走，并设计出如何能让机器人自动判断最短路程于最短时间下行走路线的问题。

所以解决好本题可以为我们的生活提供帮助。

本文通过运用两点之间直线最短理论，优化问题，最短路问题，图论，以及运用matlab软件编程及作图的方法，阐述了机器人避障问题的相对优化方案的解决办法，即“两点之间直线最好，转弯半径最小”的理论，通过计算中的比较与选择把四条最短路径都求出了相对最优解，论证了转弯速度不会随着r的增加一直增大或减小，而是有一个最小极点的思想。

从而求出了r，以及最短的时间。

问题一，通过对最短路问题的分析，我们很容易分解成线圆结构来求解，然后把可能路径的最短路径采用穷举法列举出来，最终得出最短路径：O→A 最短路径为：471.0372O→B 最短路径为：838.0466O→C 最短路径为：1085.7531O→A→B→C→O最短路径为：2834.6591问题二，通过建立时间t与r的关系式，得出r在11.504时，从O到A的时间相对最短，最短时间为98.606004。

我们可以利用此篇论文解决生活中实际的问题，在计算时可以节省大量的时间，使机器人又准确又完善的完成我们给定的任务，从而进行拓展，给定区域内任何两个点，我们都可求出其最短路径和走完全程的最快时间。

从而可以让机器人帮助我们给家里打扫卫生或设计自动吸尘器等，也可使机器人在最短的时间完成工作，提高效率，延长机器人的使用寿命。

关键字：最短路问题优化问题 matlab一问题重述随着现代科学技术日新月异的发展，机器人越来越多的出现在日常生活中,它既可以通过运行预先编排的程序为人类服务，根据人工智能程序自动处理一些生活中问题，进而协助或者相应地取代人类的工作，可以说机器人的创新与改进正一步步影响着人类的发展。

机器人避障问题摘要：当今科学技术日益发达，高科技产品尤其是机器人在我们日常生活中运用的越来越广泛，它能够代替人类完成许许多多的工作，但如何能让机器人自动化的完成人类交给的任务成为设计机器人的关键。

我们做此题就是为了更好的利用机器人为我们提供方便，提高生活质量，若机器人程序设计不当不仅不会给人类带来方便，还很有可能给我们的生活带来更多的麻烦。

本题中提出了如何让机器人能够自动识别障碍物，保证机器人能够在合理区域行走，并设计出如何能让机器人自动判断最短路程于最短时间下行走路线的问题。

所以解决好本题可以为我们的生活提供帮助。

本文通过运用两点之间直线最短理论，优化问题，最短路问题，图论，以及运用matlab软件编程及作图的方法，阐述了机器人避障问题的相对优化方案的解决办法，即“两点之间直线最好，转弯半径最小”的理论，通过计算中的比较与选择把四条最短路径都求出了相对最优解，论证了转弯速度不会随着r的增加一直增大或减小，而是有一个最小极点的思想。

从而求出了r，以及最短的时间。

问题一，通过对最短路问题的分析，我们很容易分解成线圆结构来求解，然后把可能路径的最短路径采用穷举法列举出来，最终得出最短路径：O →A 最短路径为：471.0372O →B 最短路径为：838.0466O →C 最短路径为：1085.7531O→A→B→C→O最短路径为：2834.6591问题二，通过建立时间t与r的关系式，得出r在11.504时，从O到A的时间相对最短，最短时间为98.606004。

我们可以利用此篇论文解决生活中实际的问题，在计算时可以节省大量的时间，使机器人又准确又完善的完成我们给定的任务，从而进行拓展，给定区域内任何两个点，我们都可求出其最短路径和走完全程的最快时间。

从而可以让机器人帮助我们给家里打扫卫生或设计自动吸尘器等，也可使机器人在最短的时间完成工作，提高效率，延长机器人的使用寿命。

关键字：最短路问题优化问题 matlab一 问题重述 随着现代科学技术日新月异的发展，机器人越来越多的出现在日常生活中,它既可以通过运行预先编排的程序为人类服务，根据人工智能程序自动处理一些生活中问题，进而协助或者相应地取代人类的工作，可以说机器人的创新与改进正一步步影响着人类的发展。

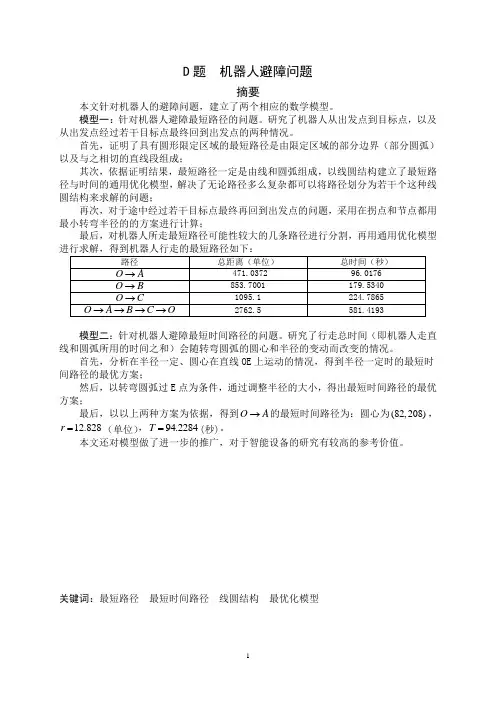
D题机器人避障问题摘要本文针对机器人的避障问题，建立了两个相应的数学模型。

模型一：针对机器人避障最短路径的问题。

研究了机器人从出发点到目标点，以及从出发点经过若干目标点最终回到出发点的两种情况。

首先，证明了具有圆形限定区域的最短路径是由限定区域的部分边界（部分圆弧）以及与之相切的直线段组成；其次，依据证明结果，最短路径一定是由线和圆弧组成，以线圆结构建立了最短路径与时间的通用优化模型，解决了无论路径多么复杂都可以将路径划分为若干个这种线圆结构来求解的问题；再次，对于途中经过若干目标点最终再回到出发点的问题，采用在拐点和节点都用最小转弯半径的的方案进行计算；最后，对机器人所走最短路径可能性较大的几条路径进行分割，再用通用优化模型进行求解，得到机器人行走的最短路径如下：路径总距离（单位）总时间（秒）→ 471.0372 96.0176O A→853.7001 179.5340O B→1095.1 224.7865O C→→→→2762.5 581.4193 O A B C O模型二：针对机器人避障最短时间路径的问题。

研究了行走总时间（即机器人走直线和圆弧所用的时间之和）会随转弯圆弧的圆心和半径的变动而改变的情况。

首先，分析在半径一定、圆心在直线OE上运动的情况，得到半径一定时的最短时间路径的最优方案；然后，以转弯圆弧过E点为条件，通过调整半径的大小，得出最短时间路径的最优方案；最后，以以上两种方案为依据，得到O A→的最短时间路径为：圆心为(82,208)，T=(秒)。

12.828r=（单位），94.2284本文还对模型做了进一步的推广，对于智能设备的研究有较高的参考价值。

关键词：最短路径最短时间路径线圆结构最优化模型1问题重述1.1 背景资料（1）图1（见附录B ）在原点O(0,0)处有一个机器人，它只能在一个800×800的平面场景范围内活动。

而图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，其障碍物的数学描述如表（见附录A ）。

机器人避障数学建模
机器人避障的数学建模通常涉及到使用传感器获取环境信息，通过算法处理这些信息，使得机器人能够避开障碍物。

以下是一个简化的数学建模示例：
1.坐标表示：用\((x,y)\)表示机器人在平面上的位置。

2.障碍物表示：用\((x_o,y_o)\)表示障碍物的位置。

3.距离计算：使用欧几里得距离或其他距离度量方法，计算机器人与障碍物之间的距离。

\[d=\sqrt{(x-x_o)^2+(y-y_o)^2}\]
4.避障算法：根据距离和传感器信息，制定避障算法。

例如，可以采用简单的规避方式，如果检测到障碍物在一定范围内，机器人就执行避障动作。

5.路径规划：考虑机器人的目标位置，通过路径规划算法（如A*算法）计算机器人避开障碍物的最优路径。

6.实时更新：在机器人移动的过程中，持续使用传感器获取新的环境信息，实时更新机器人的位置和障碍物的位置，以保持避障的准确性。

这只是一个简单的示例，实际的机器人避障数学建模可能涉及更复杂的算法和传感器数据处理。

在实际应用中，常见的传感器包括激光雷达、超声波传感器、摄像头等。

机器人避障问题摘要本文研究了在已知区域障碍物分布的情况下，机器人从起点到目标点避障最短路径或最短时间路径的问题，路径必须是由圆弧和与之相切的直线段组成的线圆结构。

一开始先对模型预处理，将所有障碍物外扩10个单位长度，划定危险区域，得到障碍扩展图。

针对问题一，经过分析论证，无论起点到目标点间危险区域有多少，最短路径都应该是紧绕危险点的切线圆路径，且可根据需依次绕过的危险点情况划分为N条子路径（见图5.1.2）求解，圆弧段取允许最小转弯半径。

模型求解分两步走：一、将实际障碍图转化为加权可视图，利用Dijstra算法搜索出在可视图下的最短路径，主要是找到必须绕过的若干危险点。

二、根据障碍扩展图将可视图中的路径修正为实际情况下的切线圆路径，求出最终结果。

在求解过程中运用MATLAB数学软件给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心连接两条切线，使机器人总的行走时间最短。

而圆弧可以有圆心坐标和半径唯一确定。

由此构建机器人行走总时间的目标函数，将机器人不与障碍物碰撞作为约束条件，将该问题转变为一个非线性规划问题，借助matlab求得最优解为:T=94.3314s。

关键词：路径规划最优化模型切线圆路径 Dijstra算法非线性规划matlab求解一、问题重述图1是一个800×800的平面场景图，在原点O(0,0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为50=v 个单位/秒。

机器人避障问题摘要我们了解到我们需要解决的是机器人从O→A、O→B、O→C和O→A→B→C→O的最短路径以及O→A的最短时间问题，但与传统的问题相比因为有了障碍物的制约使得部分区域无法通过，而且物体的运动轨迹也会对其速度造成制约，联系现实生活我们知道对于无法以最短直线路径通过时如果两点间有一根足够长的绳子，在绕开障碍物及其所影响的范围后绳子绷紧状态下所形成的轨迹即为最短路径，在最短的路径和最快的速度间找制约点可获得最短时间，该题时间制约因素为。

受此启发，在分析问题后我们建立了数学模型来合理解决如何使机器人避障的优化问题。

针对问题一；问题一中O→A可简化为两点避开单个障碍物的问题、O→B、O→C为两点避开多个障碍物的问题、对于O→A→B→C→O是一个回路的多点避开多个障碍物的问题，运用几何的求解方式证明。

针对问题二；问题二是时间最优的问题，我假设存在个半径为最优时间半径，然后我们找到个最优圆弧圆心的位置，圆心在两点连线为X轴的最高障碍点作X轴的该条垂线上。

关键词最短路径最优化模型几何求解最短时间一、问题重述1.1、基本情况:在给定的平面场景中，要求机器人绕开障碍物到达指定的目标点（要求目标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

1.2、相关信息：(1) 机器人直线行走的最大速度为50=v 个单位/秒。

(2) 机器人转弯时，最大转弯速度为21.0100e1)(ρρ-+==v v v ，其中ρ是转弯半径。

如果超过该速度，机器人将发生侧翻，无法完成行走。

1.3、需要解决的问题：(1) 机器人从O(0, 0)出发，O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径。

关于机器人避障行走问题的研究摘要本课题主要研究机器人避障行走问题，机器人行走过程，需躲避障碍物区域且保证所经路径按直线段和圆弧进行行走。

依据题目要求最短路径和最短时间路径目标，运用穷举法，先绘制出可能是最短路径的行走路线。

然后，利用平面解析几何知识，求解各路线长度并进行比较，找出最短路径。

最后，引入机器人速度数据，建立数学模型，求解出最短时间路径。

问题一、根据题目限定的机器人和障碍物之间10个单位的距离要求，先绘制出机器人能够行走的活动区域。

然后，利用平面几何知识，列出线段与圆弧结构下的行走路程关于圆弧半径的函数关系式。

运用求导法则对所列函数关系式进行求导，得出结论：只有当圆弧半径最小时（最小半径为10），才能使线弧结构的路程达到最小。

依据所得结论，运用穷举法列出从原点出发到各个目标点的所有可能最短路径。

分别进行求解并互相比较，最终得出机器人行走到不同目标点的最短路径为：O→A：471.0372；O→B：853.702132；O→C：1053.140；O→A→B→C→O：2707.4379。

（注：路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标，可通过将坐标点设定成未知量，列函数方程组编写LINGO程序进行求解得出。

起点、终点及圆弧圆心的具体坐标，见各路径模型求解部分所列坐标表格。

）问题二、路线制定过程中，引入机器人直线速度和转弯速度数据。

以行走到目标点A花费时间最短为目标建立优化模型。

根据模型，编写LINGO程序，求解出最短时间路径下，机器人过点A的圆弧圆心为（82.04274,210），圆弧半径为10.97436，花费的最短时间为94.34632。

关键词：穷举法求导法则平面几何优化模型最短时间路径1问题重述1.1问题背景进入科技时代以来，随着信息技术的不断发展，机器人自动化研究越来越成为人们关注的重点，机器人避障行走问题也成为机器人程序设定的一个常见问题。

而路线制定过程中，行走线路制定方法的研究和精确坐标数据的计算是必不可少的，且对今后机器人行进程序的设定具有很好的参考价值。

机器人避障问题一、摘要本文讨论了机器人在平面场景中避障行走的问题，已知机器人的行走模式（直线与相切圆弧）以及场景障碍物的分布，计算出到平面各个给定点的最短路径，以及到A 点的最短时间。

文中，首先，考虑到机器人与障碍物之间有10个单位的碰撞距离，故用CAD 软件将平面场景图进行改进，再用CAD 设计可能的最短路径。

接着，对每条具体路径进行分解，得到三种基本线圆形模型（点圆模型，双圆异侧模型，双圆同侧模型），对这三种模型进行求解，得到各个模型直线长度以及转弯圆弧圆形角的表达公式。

之后，参照具体的行走路径，构造合适的行走矩阵，用以判断每段路径所属的基本模型。

路径总的长度可用如下公式表达：12,1,1,211N N i i i i i i i s m r θ--+++===+⨯∑∑最后，通过计算设计的集中可能的最短路径，我们得到每段的最短路径的长度分别为：O ——A 路段：471.0372（单位）； O ——B 路段: 853.7001（单位）； O ——C 路段:3100915.1⨯（单位）；O ——A ——B ——C ——O 路段:32.677810⨯（单位）。

对于问题二，我们在问题一的基础上分别利用直线最大速度和转弯最大速度计算出时间的表达式。

为了方便计算，我们将转弯圆弧的圆心定在P （80,210）（场景中正方形5的左上角），这样得到时间T 与转弯半径ρ的函数关系式：2100.10(1)(2arccos arccos)e abT v ρρρπα-⨯+⨯---=通过MATLAB 编程，画出其图像，求解得出：当半径ρ=11.435时，时间T 最小，其大小为94.5649（秒）。

关键词：最短路径 线圆模型 行走矩阵 MATLAB二、问题重述在一个800×800的平面场景图（见附录一），在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述如下表：在图中的平面场景中，障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过10个单位）。

机器人避障问题的解题分析摘要：本文对2012年全国大学生数学建模竞赛D题机器人避障问题进行了全面分析，对最短路的设计进行了理论分析和证明，建立了机器人避障最短路径的几何模型，对最短时间路径问题通过建立非线性规划模型，有效地解决了转弯半径、圆弧圆心位置和行走时间等问题。

关键词：机器人避障；最短路径；Dijkstra算法；几何模型；非线性规划模型1 引言随着科学技术的进步和计算机技术的发展，机器人的应用越来越广泛，在机器人的应用中如何使机器人在其工作围为完成一项特定的任务寻找一条安全高效的行走路径，是人工智能领域的一个重要问题。

本文主要针对在一个场景中的各种静态障碍物，研究机器人绕过障碍物到达指定目的地的最短路径问题和最短时间问题。

本文以2012年“高教社”杯全国大学生数学建模竞赛D题“机器人避障问题”为例进行研究。

假设机器人的工作围为800×800的平面正方形区域（如图1），其中有12个不同形状的静态障碍物，障碍物的数学描述（如表1）：图1 800×800平面场景图表1在原点O(0, 0)点处有一个机器人，它只能在该平面场景围活动，机器人不能与障碍物发生碰撞，障碍物外指定一点为机器人要到达的目标点。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为50=v 个单位/秒。

机器人转弯时，最大转弯速度为21.0100e1)(ρρ-+==v v v （ρ是转弯半径）。

如果超过该速度，机器人将发生侧翻，无法完成行走。

场景图中有4个目标点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，下面我们将研究机器人从O(0, 0)出发，求O→A、O→B、O→C和O→A→B→C→O的最短路径，以及机器人从O(0, 0)出发，到达A 的最短时间路径问题。

机器人障碍问题摘要本文研究了有若干障碍物的平面场景中，机器人避障行走的最短路径以及最短时间路径的问题。

针对问题一，首先给出简单证明了两个对称点绕过圆形障碍物的最短路径为两条与圆形障碍物相切的直线，加上两切点间的劣弧。

然后分了四种情况，分别给出了不同直线与圆相切时，根据各已知点坐标，求相应切点、直行路径及劣弧长度的方法。

然后在满足机器人从定点(0,0)O出发绕过障碍物，距离障碍物至少超过10个单位，不能折线转弯绕过障碍物的条件下，以前面的证明为依据，将机器人行走路径设计为由直线和圆弧组成。

针对不同的起点和终点，将总路径分解为上述四种情况，利用MATLAB6.5.1，分别求出相应的切点及各转弯圆的劣弧长，最后比较得到相对较短的行走路径。

并根据机器人在不同路径上的速度的不同，求出避障前进的最短路径时所需要的行走时间。

具体如下：→的最短路径为471.0375个单位，所需的时间为96.0177秒O A→的最短路径为812.7029个单位，所需的时间为170.5132秒O B→的最短路径为：1090.8个单位，所需的时间为222.9373秒O C→→→→的最短路径为：3137.8个单位，所需的时间为652秒。

O A B C O针对问题二，要求求出机器人从(0,0)O出发，到达A的最短时间路径。

因为机器人行走路径为直线时的速度为定值，弧线行走的速度与弧所在的圆半径有关，由此得到行走时间与圆弧半径ρ的关系式，利用高等数学的极值定理条件，估算出ρ=11.5052个单位时从O A→所需时间最短，为95.1328秒。

该模型简单、便于理解，理论性较强。

另外图形的使用，使问题更加清晰。

该模型还可用于求解设计最优路线问题。

关键词最短路径圆弧半径最短时间切点一 问题重述在一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

平面场景中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物。

基于网络图的机器人避障问题【摘要】本文研究的是机器人避障最短时间路径的问题，总体思想是：根据无约束“混合规划”模型和“Floyd算法”，得出各路径的几种短折线路线；其次通过折线路径“切线化”和“弧线化”构造出切线与圆弧的组合路径（即为可视网络图）；最终建立基于网络图的模型，并求解。

文中模型的建立与求解均基于无量纲化，所有模型均是以时间最短或路径最短为目标。

其中，第二个问题划分为两个问题进行研究。

问题（一），根据切线定理把路径优化为直线段和圆弧，建立有约束条件的“网络规划”模型，并利用“贪心算法”计算网络图中的各最短路径，得O→A、O→B、O→C 和O→A→B→C→O四条最短路径分别为471.04、852.42、1086.45、2715.24。

问题（二），是最短时间的路径问题。

根据问题（一）中的可视网络图，以“最短时间的路径”为优化目标，利用“蚁群算法”建立蚁群最优化模型，并求出最短时间对应的路径分别为94.91和473.45。

问题（三），是最短时间与路径问题。

时间和路径具有相互约束的性质，根据问题（二）中的“蚁群算法”，建立“多目标蚁群优化模型”，并利用lingo编写程序，求出最短时间与路径分别为95.25、472.07。

本文在求解过程中，运用lingo实现“混合规划”和C语言实现“贪心算法”，对二者进行综合、比较，使得结果更趋于最优化。

关键字：可视网络图; 贪心算法; 混合规划模型; 蚁群算法;多目标优化;1 问题重述一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述表（参见附件1）。

平面场景图中（参见附件2），障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。