机器人避障问题的解题分析(建模集训)

机器人避障问题Company Document number：WTUT-WT88Y-W8BBGB-BWYTT-19998机器人避障问题摘要本文研究了在一个800800⨯平面场景里，机器人通过直线和圆弧转弯，绕过障碍物，到达目标点的问题，解决了到达目标点路径最短，以及到达A 点时间最短的问题。

文章将路径划分为若干个这种线圆结构来求解。

对于途中经过节点的再到达目标点的状况，我们采用了在拐点和节点最小转弯半径的形式.问题一，将其分解成圆线结构进行求解，利用枚举法将最短路径表示出来，结果是：O A →的距离是O →B 的距离是O →C 的距离是O →A →B →C →O关键词：最短路径 最短时间 几何应用 最优化问题一 问题重述机器人从指定点到达的目标点，其行走路径由直线段和圆弧组成。

机器人转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

同时要求机器人行走线路与障碍物间的最近距离为10个单位，机器人直线行走的最大速度为50=v 个单位/秒。

机器人转弯时，最大转弯速度为21.0100e 1)(ρρ-+==v v v ，其中ρ是转弯半径。

要求建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。

对场景图中4个点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，具体计算：(1) 机器人从O(0, 0)出发，O →A 、O →B 、O →C 和O →A →B →C →O 的最短路径。

(2) 机器人从O (0, 0)出发，到达A 的最短时间路径。

并要求给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间。

二、问题分析1.问题一要求从起始点o 绕过障碍物到达目标点，并且与障碍物最小距离为10，拐弯半径越小，走的路线越接近直线，在拐弯处画一个以拐点为圆心，半径为10的圆，这样我们就可以从起始点出发，分别做圆的切线，直到终点。

机器人避障问题摘要：当今科学技术日益发达，高科技产品尤其是机器人在我们日常生活中运用的越来越广泛，它能够代替人类完成许许多多的工作，但如何能让机器人自动化的完成人类交给的任务成为设计机器人的关键。

我们做此题就是为了更好的利用机器人为我们提供方便，提高生活质量，若机器人程序设计不当不仅不会给人类带来方便，还很有可能给我们的生活带来更多的麻烦。

本题中提出了如何让机器人能够自动识别障碍物，保证机器人能够在合理区域行走，并设计出如何能让机器人自动判断最短路程于最短时间下行走路线的问题。

所以解决好本题可以为我们的生活提供帮助。

本文通过运用两点之间直线最短理论，优化问题，最短路问题，图论，以及运用matlab软件编程及作图的方法，阐述了机器人避障问题的相对优化方案的解决办法，即“两点之间直线最好，转弯半径最小”的理论，通过计算中的比较与选择把四条最短路径都求出了相对最优解，论证了转弯速度不会随着r的增加一直增大或减小，而是有一个最小极点的思想。

从而求出了r，以及最短的时间。

问题一，通过对最短路问题的分析，我们很容易分解成线圆结构来求解，然后把可能路径的最短路径采用穷举法列举出来，最终得出最短路径：O →A 最短路径为：471.0372O →B 最短路径为：838.0466O →C 最短路径为：1085.7531O→A→B→C→O最短路径为：2834.6591问题二，通过建立时间t与r的关系式，得出r在11.504时，从O到A的时间相对最短，最短时间为98.606004。

我们可以利用此篇论文解决生活中实际的问题，在计算时可以节省大量的时间，使机器人又准确又完善的完成我们给定的任务，从而进行拓展，给定区域内任何两个点，我们都可求出其最短路径和走完全程的最快时间。

从而可以让机器人帮助我们给家里打扫卫生或设计自动吸尘器等，也可使机器人在最短的时间完成工作，提高效率，延长机器人的使用寿命。

关键字：最短路问题优化问题 matlab一 问题重述 随着现代科学技术日新月异的发展，机器人越来越多的出现在日常生活中,它既可以通过运行预先编排的程序为人类服务，根据人工智能程序自动处理一些生活中问题，进而协助或者相应地取代人类的工作，可以说机器人的创新与改进正一步步影响着人类的发展。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：日期：年月日编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：赛区评阅记录（可供赛区评阅时使用）：评阅人评分备注全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：机器人避障问题摘要针对题中机器人避障最短路径问题，文章使用简化后建立的最短路径的数学模型来解决此类问题。

对于问题1，我们matlab中自带函数graphshortestpath函数求解最短路径的数学模型。

其主要思想是：首先先证明出两点之间的最短路径是由两条线段和以中间点为圆心的圆的一段圆弧组成，然后证明圆弧的半径为定值10。

然后对模型简化使模型化为标准的最短路径模型，最后用graphshortestpath函数对模型求解。

针对问题2，我们建立了优化模型。

在问题1的基础上，我们对两种行走方案进行分析，根据转弯弧的半径变化对速度的影响我们锁定到一条路径，然后利用lingo对优化模型进行求解。

关键词：graphshortestpath函数、最短路径、避障问题1、问题重述已知：在下图中原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

建模机器人避路障问题机器人避障问题摘要：本文根据题目要求，主要研究了在一个区域内有障碍物的最短路径问题。

依题意我们可以认为最短路径一定是由线和最小圆弧组成，圆心在障碍物的顶点。

对于问题一首先讨论由O 到A 的距离，为了到达目标点，我们建立了圆线模型。

将路线分为两部分：一部分是平面上的自然最短路径（即直线段），另一部分是限定区域的部分边界的半径至少十个单位以外的圆弧，得到其路径长度为2222L b r c r r θ=--,并用MATLAB 程序解得最短路径471.0372对于O 到B 的距离问题，为了到达目标点，我们需要建立圆与点圆模型，其中由于圆与圆之间的不同的位置关系，又可以分为同向相切与异向相切，同向相切时 22221212L b r c r r r o o θθ=--++，异向相切时 2222221212()2o o L b r c r r r r θθ=--++-。

由MATLAB 程序解得最短路径869.8523。

对于O 到C ，与前者的区别是障碍物大圆视为半径较大的转折弧，为了到达目标点，依旧建立圆圆结构与线圆结构模型，经MATLAB 程序解得最短路径为1011.3。

对于OABCO 的路径问题，除了用了上述提到的圆圆，线圆结构外，还建立了圆心偏移的模型（即点ABC 在相对应的弧上），A 点偏以后的坐标为（290.9,304.1），B 点偏以后的坐标为（108.23,694.32），C 点偏以后的坐标为（707.26,633.12），将OABCO 分为两部分，一部分为OABCN （730,520）的距离，另一部分为由N 回到O 的距离，两部分结果之和即为所求路径。

OABCN 的距离1.7691e+003,N 到O 为880.7744，总长为2649,6744对于问题二，我们将路线问题转化为规划问题，求的最短时间，目标函数为由LINGO 有最短时间为94.22822，切点坐标（69.80,211.98）（77.75,220.14） 圆心（82.14,207.92）。

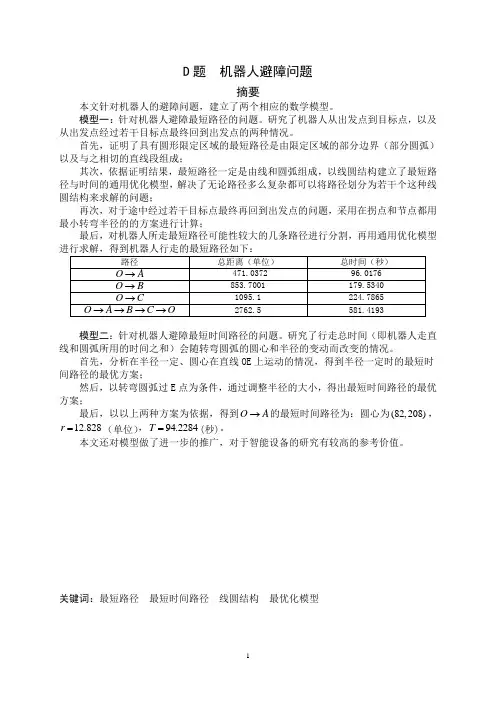
D题机器人避障问题摘要本文针对机器人的避障问题，建立了两个相应的数学模型。

模型一：针对机器人避障最短路径的问题。

研究了机器人从出发点到目标点，以及从出发点经过若干目标点最终回到出发点的两种情况。

首先，证明了具有圆形限定区域的最短路径是由限定区域的部分边界（部分圆弧）以及与之相切的直线段组成；其次，依据证明结果，最短路径一定是由线和圆弧组成，以线圆结构建立了最短路径与时间的通用优化模型，解决了无论路径多么复杂都可以将路径划分为若干个这种线圆结构来求解的问题；再次，对于途中经过若干目标点最终再回到出发点的问题，采用在拐点和节点都用最小转弯半径的的方案进行计算；最后，对机器人所走最短路径可能性较大的几条路径进行分割，再用通用优化模型进行求解，得到机器人行走的最短路径如下：路径总距离（单位）总时间（秒）→ 471.0372 96.0176O A→853.7001 179.5340O B→1095.1 224.7865O C→→→→2762.5 581.4193 O A B C O模型二：针对机器人避障最短时间路径的问题。

研究了行走总时间（即机器人走直线和圆弧所用的时间之和）会随转弯圆弧的圆心和半径的变动而改变的情况。

首先，分析在半径一定、圆心在直线OE上运动的情况，得到半径一定时的最短时间路径的最优方案；然后，以转弯圆弧过E点为条件，通过调整半径的大小，得出最短时间路径的最优方案；最后，以以上两种方案为依据，得到O A→的最短时间路径为：圆心为(82,208)，T=(秒)。

12.828r=（单位），94.2284本文还对模型做了进一步的推广，对于智能设备的研究有较高的参考价值。

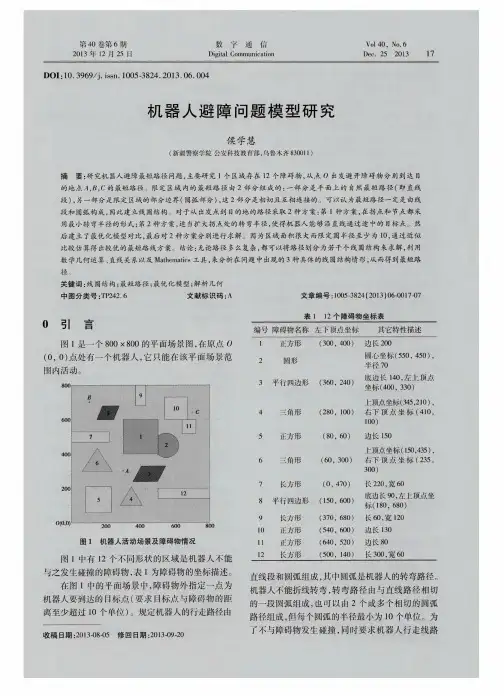
关键词：最短路径最短时间路径线圆结构最优化模型1问题重述1.1 背景资料（1）图1（见附录B ）在原点O(0,0)处有一个机器人，它只能在一个800×800的平面场景范围内活动。

而图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，其障碍物的数学描述如表（见附录A ）。

机器人避障的原理及分析机器人避障的原理和分析是指机器人在感知到障碍物时，能够自动进行规避或避免碰撞的能力。

这种能力对于机器人在各种环境中的自主移动和安全运行至关重要。

下面我们将从机器人感知技术、决策算法和执行控制三个方面来分析机器人避障的原理。

机器人的感知技术是实现避障的基础。

一般来说，机器人感知障碍物主要通过以下几种传感器实现：1.超声波传感器：超声波传感器通过发送超声波信号并计算信号的反射时间来确定物体与机器人之间的距离。

根据距离信息，机器人可以判断是否需要避障。

2.激光雷达：激光雷达是一种高精度测距传感器，能够测量物体与机器人之间的精确距离和方位信息。

通过激光雷达，机器人可以获得详细的环境地图，从而有效地规避障碍物。

3.视觉传感器：视觉传感器一般使用相机或摄像头，通过图像处理和计算机视觉算法来识别、跟踪和测量障碍物。

视觉传感器可以提供丰富的环境信息，但在复杂环境或光线不足时可能受到限制。

决策算法是机器人避障的核心。

一般来说，决策算法会根据传感器获得的环境信息进行分析和判断，并采取相应的措施规避障碍物。

常见的决策算法有：1.基于规则的方法：基于规则的决策算法将预先定义的规则应用于感知到的环境信息，从而判断机器人应该采取的动作。

例如，如果机器人检测到前方有障碍物，则应该停止或绕过障碍物。

2.基于学习的方法：基于学习的决策算法使用机器学习技术，通过分析大量的训练数据来学习如何判断和规避障碍物。

这种方法可以适应不同的环境和障碍物类型，具有较高的智能性和灵活性。

执行控制是机器人避障的最后一步。

一旦决策算法确定了机器人应该采取的动作，执行控制系统会将指令传达给机器人的执行器，如电机或轮子，以实现相应的运动。

执行控制系统需要与感知技术和决策算法紧密协作，确保机器人能够及时、准确地避开障碍物。

总体而言，机器人避障的原理是通过感知技术获取环境信息，利用决策算法分析和判断障碍物，然后通过执行控制系统执行相应的运动。

机器人避障问题的解题分析摘要：本文对2012年全国大学生数学建模竞赛D题机器人避障问题进行了全面分析，对最短路的设计进行了理论分析和证明，建立了机器人避障最短路径的几何模型，对最短时间路径问题通过建立非线性规划模型，有效地解决了转弯半径、圆弧圆心位置和行走时间等问题。

关键词：机器人避障；最短路径；Dijkstra算法；几何模型；非线性规划模型1 引言随着科学技术的进步和计算机技术的发展，机器人的应用越来越广泛，在机器人的应用中如何使机器人在其工作围为完成一项特定的任务寻找一条安全高效的行走路径，是人工智能领域的一个重要问题。

本文主要针对在一个场景中的各种静态障碍物，研究机器人绕过障碍物到达指定目的地的最短路径问题和最短时间问题。

本文以2012年“高教社”杯全国大学生数学建模竞赛D题“机器人避障问题”为例进行研究。

假设机器人的工作围为800×800的平面正方形区域（如图1），其中有12个不同形状的静态障碍物，障碍物的数学描述（如表1）：图1 800×800平面场景图表1在原点O(0, 0)点处有一个机器人，它只能在该平面场景围活动，机器人不能与障碍物发生碰撞，障碍物外指定一点为机器人要到达的目标点。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为50=v 个单位/秒。

机器人转弯时，最大转弯速度为21.0100e1)(ρρ-+==v v v （ρ是转弯半径）。

如果超过该速度，机器人将发生侧翻，无法完成行走。

场景图中有4个目标点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，下面我们将研究机器人从O(0, 0)出发，求O→A、O→B、O→C和O→A→B→C→O的最短路径，以及机器人从O(0, 0)出发，到达A 的最短时间路径问题。

机器人障碍问题摘要本文研究了有若干障碍物的平面场景中，机器人避障行走的最短路径以及最短时间路径的问题。

针对问题一，首先给出简单证明了两个对称点绕过圆形障碍物的最短路径为两条与圆形障碍物相切的直线，加上两切点间的劣弧。

然后分了四种情况，分别给出了不同直线与圆相切时，根据各已知点坐标，求相应切点、直行路径及劣弧长度的方法。

然后在满足机器人从定点(0,0)O出发绕过障碍物，距离障碍物至少超过10个单位，不能折线转弯绕过障碍物的条件下，以前面的证明为依据，将机器人行走路径设计为由直线和圆弧组成。

针对不同的起点和终点，将总路径分解为上述四种情况，利用MATLAB6.5.1，分别求出相应的切点及各转弯圆的劣弧长，最后比较得到相对较短的行走路径。

并根据机器人在不同路径上的速度的不同，求出避障前进的最短路径时所需要的行走时间。

具体如下：→的最短路径为471.0375个单位，所需的时间为96.0177秒O A→的最短路径为812.7029个单位，所需的时间为170.5132秒O B→的最短路径为：1090.8个单位，所需的时间为222.9373秒O C→→→→的最短路径为：3137.8个单位，所需的时间为652秒。

O A B C O针对问题二，要求求出机器人从(0,0)O出发，到达A的最短时间路径。

因为机器人行走路径为直线时的速度为定值，弧线行走的速度与弧所在的圆半径有关，由此得到行走时间与圆弧半径ρ的关系式，利用高等数学的极值定理条件，估算出ρ=11.5052个单位时从O A→所需时间最短，为95.1328秒。

该模型简单、便于理解，理论性较强。

另外图形的使用，使问题更加清晰。

该模型还可用于求解设计最优路线问题。

关键词最短路径圆弧半径最短时间切点一 问题重述在一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

平面场景中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物。

机器人避障数学建模
机器人避障的数学建模通常涉及到使用传感器获取环境信息，通过算法处理这些信息，使得机器人能够避开障碍物。

以下是一个简化的数学建模示例：
1.坐标表示：用\((x,y)\)表示机器人在平面上的位置。

2.障碍物表示：用\((x_o,y_o)\)表示障碍物的位置。

3.距离计算：使用欧几里得距离或其他距离度量方法，计算机器人与障碍物之间的距离。

\[d=\sqrt{(x-x_o)^2+(y-y_o)^2}\]
4.避障算法：根据距离和传感器信息，制定避障算法。

例如，可以采用简单的规避方式，如果检测到障碍物在一定范围内，机器人就执行避障动作。

5.路径规划：考虑机器人的目标位置，通过路径规划算法（如A*算法）计算机器人避开障碍物的最优路径。

6.实时更新：在机器人移动的过程中，持续使用传感器获取新的环境信息，实时更新机器人的位置和障碍物的位置，以保持避障的准确性。

这只是一个简单的示例，实际的机器人避障数学建模可能涉及更复杂的算法和传感器数据处理。

在实际应用中，常见的传感器包括激光雷达、超声波传感器、摄像头等。

机器人避难问题分析2012高教社杯全国大学生数学建模竞赛题目个人解析-----D题机器人避障问题图1是一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述如下表：编号障碍物名称左下顶点坐标其它特性描述1正方形(300, 400)边长2002圆形圆心坐标(550, 450)，半径703平行四边形(360, 240)底边长140，顶点坐标(400, 330)4三角形(280, 100)上顶点坐标(345, 210)，右下顶点坐标(410, 100)5正方形(80, 60)边长1506三角形(60, 300)上顶点坐标(150, 435)，右下顶点坐标(235, 300)7长方形(0, 470)长220，宽608平行四边形(150, 600)底边长90，左上顶点坐标(180, 680)9长方形(370, 680)长60，宽12010正方形(540, 600)边长13011正方形(640, 520)边长8012长方形(500, 140)长300，宽60在图1的平面场景中，障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为个单位/秒。

机器人转弯时，最大转弯速度为，其中是转弯半径。

如果超过该速度，机器人将发生侧翻，无法完成行走。

请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。

机器人避障问题摘要本文研究了机器人避障最短路径和最短时间路径的问题，主要研究在一个存在12个障碍物的区域中，由出发点到达目标点以及由出发点经过途中的若干目标点到达最终目标点两种情形，要得出机器人到达目标点的最短路径，我们将路径分为两个部分组成：一部分是平面上的自然最短路径（即直线段），另一部分则是限定区域（即圆弧）。

针对问题一，我们将直线和圆弧组成的路径作为机器人行走的最短路径，因此我们建立了线圆结构并构造直角三角形，运用勾股定理与两点之间的距离建立相应方程，无论多么复杂的路径，我们都可以将路径划分为若干个这种线圆结构来求解。

我们利用线圆结构方法对机器人到达目标点的每一条路径进行分解，然后把几条最短路径采用穷举法列举出来，通过比较得出最优路径分别为（详细的坐标路线见模型的建立于求解部分）：1076.6094 2602.3058O A O B O C O A B C O →→→→→→→的最短路径的总距离为471.0372，的最短路径的总距离为845.7001，的最短路径的总距离为，的最短路径的总距离为。

针对问题二，要求得机器人从O(0，0)到达A 点的最短时间路径，由题意我们知道机器人的直线行走速度是一定的，所以我们考虑到增加机器人转弯时的转弯半径，从而增加转弯速度，相应的O A →长度也发生了变化。

针对这个问题我们根据机器人的最大转弯速度与问题一的分析，通过Matlab 计算可得当12ρ=时，机器人从O 点出发到A 的时间最短为94.6001秒。

关键词：线圆结构 勾股定理 穷举法 最优路径 机器人避障—、问题重述1.1 背景分析机器人是整合控制论、机械电子、计算机、材料和仿生学的产物。

在工业、医学、农业、建筑工业甚至军事领域中均有重要用途。

现在。

，国际上对机器人是靠自身动力和控制能力来实现各种功能的一种机器。

联合国标准化组织采纳了美国机器人协会给机器人下的定义：“一种可编程和多功能的操作机；或是为了执行不同的任务而具有可用电脑改变和可编程动作的专门系统。

机器人避障问题摘 要本文讨论的是机器人避障问题，运用改良的橡皮筋算法思想，对最优路径逐步探索，并进行了大胆猜想．通过分析，利用几何关系证明了猜想的正确性，以此得到判断最短路径的三个原则：一、所走路线应尽可能接近两目标点与目的地连线；二、目标点转弯半径越小越好；三、找不到两圆间的公切线时，机器人应尽可能沿障碍物边界运动． 对于问题一，依据路径最优原则，确定转弯半径为10个单位，建立了机器人从区域中一点到达另一点的避障最短路径的优化模型．利用MATLAB 求解得到结果如下：A O →:总时间为：96.00826秒，总路程为471.0372个单位；B O →:总时间为179.09982秒，总长度为853.7113单位；C O →:总时间为239.72602秒，总路程为1100.19单位；O C B A O →→→→：总路程：2794.512单位 ，最终总时间为598.5477秒．对于问题二，要使机器人行走时间最短，需在尽可能保证最短路径的基础上适当增加转弯半径．利用几何知识推导出机器人行走时间与转弯半径的关系，时间对半径求导，并令导数为零，得出最短时间所对应的半径5055.11=r ，进而建立最短时间路径的优化模型．利用MATLAB 软件求解得，当机器人从)0,0(O 出发到达A 时，所用最短时间为2130.94秒，总距离为470.8301个单位．关键词：导数；橡皮筋算法；优化模型一、问题的重述图1是一个800⨯800的平面场景图，在原点)0,0(O 点处有一个机器人，它只能在该平面场景范围活动．图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物单位数学描述如下表：表1．12个不同形状区域的特性障碍物的距离至少超过10个单位）．规定机器人的行走路线有直线段和圆弧组成，其中圆弧是机器人的转弯路径．机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位．为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若发生碰撞，则机器人无法完成行走．机器人直线行走的最大速度为50=v 个单位/秒．机器人转弯时，最大转弯速度为21.01001)(ρρ-+==e v v v ，其中ρ是转弯半径．如果超过该速度，机器人将发生侧翻，无法完成行走．请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型．对场景图中4个点)0,0(O ，)300,300(A ，)700,100(B ，)640,700(C ，具体计算：（1）机器人从)0,0(O 出发，A O →、B O →、C O →和O C B A O →→→→的最短路径．（2）机器人从)0,0(O 出发，到达A 的最短时间路径．注：要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间 ．图1 800⨯800平面场景图二、问题分析对题目条件进行分析：要求目标点与障碍物的距离至少超过10个单位，又知O 点坐标为（0,0），即边界不视为障碍物，但目标点不能超出界限．规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径，转弯路径只能由一段圆弧组成也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位，因为半径趋于0的时候，圆弧长度趋于0，圆弧趋于折线．机器人行走路径与障碍物之间的最近距离为10个单位，否则发生碰撞，即可将障碍物区域向外扩充10个单位，余下部分为目标点可行走范围，对条件中所给最大转弯速度21.01001)(ρρ-+==e v v v 进行分析，当半径∞→ρ时，即可视为直线运动，50==v v 个单位/秒；当半径10→ρ时，最小速度5.220min ==v v 个单位/秒；半径ρ越大，机器人转弯速度越大． 对问题一分析：机器人从)0,0(O 出发，A O →、B O →、C O →和O C B A O →→→→的最短路径问题．首先分析A O →，在没有障碍物的情况下，A O →两点间线段最短，但在两点之间有正方形障碍物5阻碍，必须绕开障碍物5到达A ，要使A O →路径最短，则实际路径越逼近OA 线段越短．根据目标点的位置，可以猜想出机器人的几种避障路径．同理分析B O →、C O →路段．当分析O C B A O →→→→路径时，采用分段处理的方法，将其分为A O →、B A →、C B →、O C →；使各分段路径最短，最后将分段路径综合起来也是最短．对问题二分析：机器人从)0,0(O 出发，到达A 的最短时间路径．在前文条件分析中，半径ρ越大，机器人转弯速度越大，速度v 越大．在问题一最短路径基础上，在转弯路段进行优化处理，适当增大转弯半径ρ，速度增大，与此同时转弯路段圆弧长度必然增加，综合使得到达目的地总时间最短．最后将给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间 ．三、模型假设1．假设机器人在行进过程中为质点；2．假设机器人直线路段以速度50=v 个单位/秒行进；3．假设机器人在各转弯路段匀速行进；4．假设机器人从直线段至圆弧段，速度由直线行进速度瞬间降至转弯速度，速度不存在过度阶段；5．假设平面范围边界不是障碍物，不要求目标点与边界的距离至少超过十个单位，机器人目标点不出界即可．四、符号说明i l 表示机器人每段路径，2,1=i ；r 表示转弯半径；i t 表示机器人所用时间，2,1=i ；i ω表示 第i 段圆弧对应的圆心角；⎩⎨⎧=,0,1其它个切点与目标点相连个障碍物第第j i m ij ； ),(ij ij ωτ表示切点坐标．五、模型的建立与求解问题一模型的建立模型准备：根据对问题的分析及两点之间直线最短的原理，为使机器人能以最短的路径避过障碍达到目标点，应使所走的路线尽可能的接近两目标点的连线，对此，可以猜想出几种机器人行走的路径并对其进行探索．首先对机器人所能行走的区域进行分析，根据题意，需要将区域向外扩展10个单位，区域边界角也应扩展10个单位，即机器人能运动范围是由4/1圆弧和相应的线段围成的，具体结果如下图1所示：200400600800Y图1：机器人行走范围图假设机器人可以看成是一个支点，则机器人可以在边界线上运动而不会发生碰撞．为使得机器人能以最短路径避过障碍物，首先进行局部分析，考虑A O →段路径，由图可知：（1）若无障碍物，A O →最短路径为OA 线段；（2）A O →路段被障碍物5阻隔最短路径探索．探索最短路径原则：实际路径越逼近OA 线段越优．①先不考虑弧长问题，探索大致路径.图3（a ）.路径一 图3（b ）路径二路径一是机器人在保证尽量沿边界线运动的情况下得到的．要从O 点到达A 点，机器人必须绕过边界角，根据两点之间直线最短的原理，可以得到图3（b ）的路径二．通过比较，可以得出：在尽可能沿OA 路径行走的前提下，不需要转弯就能到达的路径尽量选用直线路径，减少圆弧路径阶段，使路径得到优化．②转弯圆弧半径相等时，目标点在不同地点转弯，探索较优路径．2B如图所示，三段弧33B A 、22B A 、11B A 对应圆半径相等且依次远离障碍物,离AB 线段的距离越来越远．以A 为圆心，3AA 为半径画弧，分别交1A 、2A ;同理以B 为圆心，3BB 为半径画弧； 即3AA =2AA =1AA ，3BB =2BB =1BB ；显然11B A →的距离最大，22B A →距离次之，33B A →距离最小；所以由B A →最段路径选择B B A A →→→33．由此可得出结论：在确定转弯圆弧半径的情况下，机器人转弯越靠近障碍物，行走路线越接近两目标点之间的连线，总路程越小．③在距障碍物最近的前提下，考虑圆弧半径的影响，确定最短路径．自定义：边界圆弧中点称为节点．通过②中结论可知：在确定转弯圆弧长度的情况下，机器人转弯越靠近障碍物，行走路线越接近两目标点之间的连线，总路程越小．由机器人所能行走的区域范围及转弯半径至少为10的约束可知，画出的4/1圆弧边界是机器人行走最短路径的边界，若需增大转弯半径，只能在节点处进行变化，否则将超出机器人行走范围．节点是边界圆弧的中点．现判断在节点处，转弯半径对最优路径选择的影响．各图形顶角所对应的外围10个单位区域为边界圆弧，该圆弧为转弯最小圆弧．过最小圆弧节点做与节点相切的半径大于10个单位的圆及相应的路径，如下图3（c ）中的2号路径．图3．（c ）路径三可做如下猜想：圆弧的半径越小，机器人从第一个目标点到达目的地总路程越小．下面对猜想进行证明：A图4：证明猜想示意图如图4所示，以O 为圆心，半径为r 画圆，BD 与圆O 相切，切点为D ，AC 与与圆O 相切，切点为C ；角ωγβα,,,位置如图所示．设A 点坐标为),(11b a ,B 点坐标为),(22b a ,圆心O 点坐标为),(y x ．AC =1l ，CD 弧长=2l ，BD =3l ,由几何知识可得： 2121)()(a x b y a -+-=，2222)()(a x b y b -+-=，212212)()(b b a a c -+-=，在C Rt AO ∆和BOD Rt ∆中，可得：a r=αcos ，b r=γcos ，由余弦定理得： ab c b a 2cos 222-+=β，B A →总路程为=L 1l ＋2l ＋3l ，221r a AC l -==,223r b BD l -==，=L 22r a -+22r b -+r ⋅ω，γβαπω---=2，∴总长度L 与转弯半径r 的关系式为：=L 22r a -+22r b -+r ⋅---)2(γβαπ，为寻求总长度L 与转弯半径r 的具体关系，将L 对半径r 求导，即:)arccos arccos 2(2222b r a r rb r r a r dr dL ---+--+--=βπ )1111(2222b r b a rar -+-+ 化简得：br a r dr dL arccos arccos 2---=βπ， πβ<，当且仅当O B A ,,三点共线时，πβ=，此种情况下不存在两个切点． 角γα,均在直角三角形内，非直角，∴πγα<+． 综上所述：0arccos arccos 2>---=br a r dr dL βπ． 即：总路程L 关于半径r 的函数单调递增，机器人从一个目标点到另一个目的点行走的总路程随着转弯圆弧半径增大而增加．故，猜想：圆弧的半径越小，机器人从第一个目标点到达目的地总路程越小，是正确的．由于机器人转弯半径至少为10个单位，要使行走路径最短，转弯半径10=R .经过上述对机器人避障路线的探究，可得为使机器人行走最短路径，需遵循以下几个原则：1.所走路线应尽可能接近两目标点的连线；2.转弯半径越小越好；3．找不到两圆间的公切线时，机器人应尽可能的沿障碍物边界运动．模型的建立：根据以上原则，可以建立机器人从一个目标点到达另一个目标点的最短路径优化模型．设切点坐标为),(ij ij ωτ，表示第i 个障碍物第j 个切点．通过对路径的探索，可知机器人的路径是由直线和一条或多条圆弧组成的．在此模型中，假设机器人的路径是分阶段的，每一阶段的路径由一条线段和一段圆弧组成，包括了一条线段和多条圆弧的情况．如第１段路径中，线段和圆弧相连，在第２段路径中，线段与第１段路径中的圆弧相连，当此线段长度为０时，机器人从第１段起点到第２段末点的路径就是由一条线段和两段圆弧组成的．线段的长度1l 可由两点间的距离公式解得：2122121)()(y y x x l -+-=．圆弧的角度为ω，半径为r ，则圆弧弧长2l ：ω⋅=R l 2．已知切点时，圆弧角度ω为：R y y x x 2)()(arcsin 2212212-+-⨯=ω．机器人从第一个目标点（11,n m ）到第二个目标点（22,n m ）过程中，⎩⎨⎧= ,0,1其它个切点与目标点相连个障碍物第第j i m ij ， 此时要避过i 个障碍点，设从第一个目标点出发到达另一处时，0=i ，则线段部分长度 :22)2)(2(22)2)(1()1()1(2)1()1(2010221102210121011)()()()()()()()(n m n m l j i j i j i j i j i j i -+-+-+-+-+-+-+-=++++++++ωτττωωττωωωτ,同理，此时对应的圆弧长度：∑=-+-⋅⨯=12122122122)()(arcsin2i i i i i R R l ωωττ.为使机器人行走路径最短，即：21min l l +.综上，可以建立最优规划模型：21min l l +∑∑==-+-⋅=2112221)()(j i k ij k ij ij n m m l ωτ ∑∑==++++-+-+120212)1()1(2)1()1()()(i j j i j i j i j i ττωω 2,1=k∑=-+-⋅=12022122122)()(arcsin2i i i i i R R l ωωττ.10=R问题二的模型建立要使机器人从一个目标点到达另一个目标点所用的时间最短，需考虑行走总路程与速度的影响．对条件中所给最大转弯速度21.01001)(ρρ-+==ev v v 进行分析可知，当半径∞→ρ时，即可视为直线运动，此时50==v v 个单位/秒；当半径10→ρ时， 最小速度5.22min ==v v 个单位/秒，即机器人的速度范围为2.5到5.且半径ρ越大，机器人转弯速度越大．所以为追求最小时间，应在模型一的基础上适当增大转弯半径．同样要保证总路程尽可能的短，机器人转弯时要接近障碍物，即所走路线应尽可能接近两目标点的连线．故可以在最小圆弧基础上增大转弯半径，以下讨论速度与半径之间的关系．如上述图4所示，总路程由线段长度和圆弧长度组成．a r =αcos ，b r =γcos ，abc b a 2cos 222-+=β，221r a AC l -==,223r b BD l -==，=L 22r a -+22r b -+r ⋅ω，γβαπω---=2，=L 22r a -+22r b -+r ⋅---)2(γβαπ，则总时间 21t t t +=，22221v r b r a t -+-=， v r t ⋅=ω2即总时间t 为：2222v r b r a v rt -+-+⋅=ω21.01001)(r ev r v v -+==t 对半径r 求导:)arccos arccos 2((122220b ra r rb r r a r v dr dt ---+--+--⨯=βπ ))2.0()arccos arccos 2(21.010r e b r r r a r r r r -⋅⋅⋅-⋅-⋅-+⋅-βπ)1())1111(21.0102222r e br b a r a r ⋅-+⨯-+-+化简得：)2.01()arccos arccos 2(221.0101.010r r e e br a r dr dt ⋅-⋅-⨯-+⋅---=βπ， 令导数 0=drdt, 由模型一可知：bra r arccos arccos 2---βπ0>,解得当5055.11=r 时，0=drdt．且函数在 )5055.11,10(∈x 区间内是单调递减的，在5055.11>x 时是逐渐增大的，故要使时间最短，满足5055.11=r ．模型的建立：模型二是在模型一的基础上增大转弯半径得到的，是追求最短时间和最短路径的双目标规划问题．建立模型如下：21 t min t +21min l l +..t s ∑=-+-⋅=1222122122)()(arcsin2i i i i i RR l ωωττ∑∑==-+-⋅=2112221)()(j i k ij k ij ij n m m l ωτ∑∑==++++-+-+120212)1()1(2)1()1()()(i j j i j i j i j i ττωω，2,1=k11v l t =， v l t 22=，.5055.11=r问题一、问题二模型的求解：根据建立的模型可利用橡皮筋算法]1[探索最短路径．机器人行走时，如果不知道确定路线时，可以先假设机器人会朝着目的地的方向走，如图3(a)中的A O →；如果中途碰到障碍物，就试图绕过障碍物，再重新朝向目的地的方向行走，如图所示A c b a O →→→→，其中绿色的圆点S 表示出发点，红圆点T 表示目的地．实际上，如果视觉上没有障碍，运动者会选择较近的直切障碍物边沿的行走路线，如图3(b)所示A c b O →→→．这种形状，就像在出发点和目的地之间拉了根橡皮筋，由于障碍物的存在，橡皮筋不能横穿过去，所以沿障碍物边沿拉伸，而正是因为橡皮筋具有的弹性，使得路径趋于最短．根据这种思路，提出了自动漫游路径生成的橡皮筋算法．根据制定的三条原则：1.所走路线应尽可能接近两目标点的连线；2.转弯半径越小越好；3．找不到两圆间的公切线时，机器人应尽可能的沿障碍物边界运动．可以得到机器人从)300,300()0,0(A O →的几条最优路线，如图5所示：200400600200400图5：A O →最短路径示意图从图中可以看出，从)300,300()0,0(A O →有两条路线需要比较计算，利用MATLAB 软件求解得到结果如下（长度单位为单位）：A O →最优路径为：A b a O →→→00．总路程分为2条线段和1段圆弧．其中，各起终点坐标、圆弧圆心坐标及相应的弧长、线段长度分别是： 线段OC ：O （0，0）→C (70.4825，213.0686) 长度224.4237弧CD ： C (70.4825，213.0686) →D （76.4914,219.3643）圆心（80,210）长度9.0041 线段DA ： D （76.4914,219.3643）→A （300,300） 长度237.6094 总时间：96.00826秒 总路程471.0372单位同理可以根据原则得到从O 到B 的几条路线，如图6所示：可编辑200400600800200400600800XY图6：B O →最短路径示意图利用MATLAB 软件求解得到结果如下： 从)700,100()0,0(B O →的最优路径为：B L K J I h f e d c b O →→→→→→→→→→→其中，各起终点坐标、圆弧圆心坐标及相应的弧长、线段长度分别是：线段: Oa )6396.301,1353.50()0,0(a O → , 长度：305.7777 弧ac : ）圆心（300,60, )5474.305()6396.301,1353.50(c a →， 弧长：4.3214 线段cd : )40.5474141.6798,4( )5474.305(d c → 长度：162.1731 弧de ： )435,150, )44.7901147.9621,4()40.5474141.6798,4(圆心（e d → 弧长：7.7751线段ef ： )60.2099222.0379,4()44.7901147.9621,4(f e → 长度： 75.6637 弧fh ： )470,220 (230,470),)60.2099222.0379,4(圆心（h f → 弧长：13.6556 线段hI ： )530,230((230,470)I h → 长度：60 弧IJ ：)530,220 , )3534.538,4967.225()530,230(圆心（J I → 弧长： 9.8883 线段JK ： ,6462915 503314435345384967225). ,.K() .,.J(→ 长度：96.9537 弧KL ： )600,150 ,)96.3458140.6916,5()91.6462144.5033,5(圆心（L K → 弧长：6.1474线段LB ：,)700,100()96.3458140.6916,5(B L → 长度：111.3553 总路程为853.7113 个单位 总时间： 811.9235秒同理可以根据原则得到从O 到C 的几条路线，如图7所示200400600800Y图7：C O →最短路径示意图机器人C O →段路径有4条，利用MATLAB 求解得出结果如下：最优路径为：C k J I H f e d c b a O →→→→→→→→→→→1111111111其中，各起终点坐标、圆弧圆心坐标及相应的弧长、线段长度分别是：线段1Oa ：)0.2262232.1149,5()0,0(1a O → 长度： 237.4868 弧11b a ：）圆心（60,230 , )5.2128238.7797,5()0.2262232.1149,5(11b a → 弧长：8.5850线段11c b ：)34.7872391.2203,3(c )5.2128238.7797,5(11→b 长度：318.4336 弧11c d ： )330,400( , )39.8254398.1397,3()34.7872391.2203,3(c 11圆心d → 弧长：8.8448线段11e d ：371.3965)(564.8828,)39.8254398.1397,3(11e d → 长度：169.7056 弧11f e ： )450,550( 400.4069),(612.7736,f 371.3965)(564.8828,11圆心→e 弧长：57.2031线段11h f ：510.0731)(718.7935,h 400.4069)(612.7736,f 11→ 长度：152.5349 弧11I h ： )520,720( (730,520),I 510.0731)(718.7935,h 11圆心→ 弧长：16.9174 线段11J I ：(730,600)J (730,520)I 11→ 长度：80弧11k J ： )600,720(, 606.3589)(727.7178,k (730,600)J 11圆心→ 弧长6.8916 线段C k 1： C(700,640) 606.3589)(727.7178,k 1→ 长度：43.5890 总路程：1001.7499+98.4401=1100.19单位 总时间：200.34998+39.37604=239.72602秒同理，找出O C B A O →→→→的最优路径，如图8所示：200400600800Y图8：O C B A O →→→→最短路径示意图利用MATLAB 求解得出各起终点坐标、圆弧圆心坐标及相应的弧长、线段长度分别是：弧22d c ：2c (292.7141, 280.3754) →2d (299.3452, 293.5596)圆心（300,300） 长度：16.5989线段22e d ：d2(299.3452, 293.5596) →2e （229.7932，532.02307）长度 248.3995 弧22f e ：2e （229.7932，532.02307）→2f （225.4967，538.3538）圆心：（220,530）长度7.8147线段22i f ：2f （225.4967，538.3538）→2i （140.4000,597.200） 长度103.4617 弧22i h ： 2h （144.5033,591.6462）→2i （140.4000,597.200）圆心（150,600） 长度7.0503线段22j i :2i （140.4000,597.200）→2j (92.000，694.000) 长度108.2257 弧22k j ： 2j (92.000，694.000) →2k （102.3208,709.7270） 圆心（100,700） 长度24.4852线段22l k ：2k （102.3208,709.7270）→2l （270,690） 长度168.8356 弧22m l ：2l （270,690）→2m （272，689.7980）圆心（180,770）， 长度2.0136线段22n m ： 2m （272，689.7980）→2n （368,670.2020） 长度97.9796 弧22o n ：2n （368,670.2020）→2o （370,670）圆心（370，680） 长度2.0136 线段22p o ： 2o （370,670）→2p （430,670） 长度60 弧22q p ： 2p （430,670）→2q （435.5878,671.7068）圆心（430,680）长度5.9291 线段22r q : 2q （435.5878,671.7068）→2r (534.4122,738.2932) 长度119.1638 弧22s r ： 2r (534.4122,738.2932) →2s （540,740）圆心（670,600） 长度5.9291 线段22t s ：2s （540,740）→2t （670,740） 长度130 弧22u t ： 2t （670,740）→2u （679.7725,732.1211）圆心（670,730）长度13.5707 线段22v u ： 2u （679.7725,732.1211）→2v （700.2275,637.8789） 长度96.4365 弧22w v ：2v （700.2275,637.8789）→2w （702.6928,633.1732）圆心（700,640） 长度5.3769最终总路程：2794.512 单位； 最终总时间：598.5477秒 问题二的求解问题二是在建立最短时间优化模型的基础上求解出从O 到A 的最短时间．根据建立的模型，可知当转弯半径5055.11=r 时，时间有最小值．因为 21.01001r ev v ⨯-+=，此时转弯时机器人的速度： 81115.4=v ． 利用问题一的方法解得各起终点的坐标、圆弧圆心坐标如下： 线段Oa ：)210,70(00a O →），（； 弧ab ：)3992.219,0916.78()210,70(b a →， 圆心为（81.5055,210）)300,300()3992.219,0916.78(A b →；总时间2130.94=t 秒， 总距离470.8301单位．模型检验对于问题一的模型检验，由于软件CAD 在处理图形、获取坐标方面较方便快捷，利用CAD 可以自动读取坐标、线段长度、弧长的优点，粗略的估计从A O →、B O →、C O →和O C B A O →→→→的可能较短路线，由CAD 软件可求得得粗略解．将在Autocad 中得到的结果与计算值相比较得表如下：短路线中的最短路径，因此本模型在解决机器人避开障碍物探索最短路径是相对较客观合理的．模型的评价与推广优点：（1）：本模型借鉴“橡皮筋算法”的精华的思想基础，并改良其不足，利用改良后的“橡皮筋算法”使解决机器人机器人避开障碍物探索最短路径的问题变得生动形象，化抽象为具体，使本模型在其它类似问题方面的迁移性较强．（2）：本模型充分体现数形结合思想，在处理机器人行走路线由直线到曲线、由曲线到直线等问题时，巧妙利用解析几何中，圆的切线、两圆公切线处理，同时，采用CAD 软件进行图像上的检验，使本模型在几何关系、数学关系上得出的结果都是客观合理的．缺点：由于行走路线的限制，且路线的连续性以及机器人只能利用圆弧拐弯，因此求出的拐点（直路线线和圆弧切的点）基本上是小数，而且本模型中只精确到0.0001，可能会给具体的机器人实践行走时带来误差．模型的推广：本模型可用于推广解决机器人快速灭火，迷宫路径探索等相似路径的探索问题，也可推广至交警疏通堵车问题中路径规划问题．参考文献[1] 陈勇，王栋，陈戈，一种三维虚拟场景自动漫游的快速路径规划算法，系统仿真学报，第19卷，第11期：2508-2510页，2007.[2] 杨文茂，李全英，空间解析几何，武汉大学出版社，2006.[3] 胡良剑，孙晓君，MATLAB数学实验，高等教育出版社，2006.附录附录1：%两圆公切线，两圆大小相等．求切点%保存为函数wfunction wa1=80+1.5055;b1=210;a2=720;b2=600;%两圆圆心坐标[x,f,h]=fsolve(@li,[a1,b1])endfunction f=li(x)a1=80+1.5055;b1=210;a2=720;b2=600;%zx=(a1+a2)/2;zy=(b1+b2)/2;%两圆相切zx=300;zy=300;%zx=0;zy=0;%直线与圆相切时f(1)=(x(1)-a1)^2+(x(2)-b1)^2-10^2;%在某圆上f(2)=(x(1)-zx)^2+(x(2)-zy)^2+10^2-((zx-a1)^2+(zy-b1)^2);%与两圆圆心连线的中点构成勾股定理end附录2：%求弧长公式要每个点迭代clear;clc;R=11.5055;x1=78.0916;y1=219.3992;%第一点坐标x2=70;y2=210;%第二点坐标f=R*2*asin(sqrt((x2-x1)^2+(y2-y1)^2)/2/R) %弧长附录3：%两圆公切线，两圆大小不等function oformat short[x,f,h]=fsolve(@laz,[580 450])endfunction f=laz(x)f(1)=sqrt((550-x(1))^2+(450-x(2))^2)/(sqrt((720-x(1))^2+(520-x(2))^2))-8;f(2)=7/17*x(1)+3800/17-x(2);end附录4：%算线段长度，要迭代clear;clc;R=10;x1=0;y1=0;%第一点坐标x2=50.1353;y2=301.6396;%第二点坐标f=sqrt((x2-x1)^2+(y2-y1)^2) %线段长度.。