大学生数学建模——机器人避障问题的研究

v1.0 可编辑可修改机器人避障问题的解题分析摘要：本文对2012年全国大学生数学建模竞赛D题机器人避障问题进行了全面分析，对最短路的设计进行了理论分析和证明，建立了机器人避障最短路径的几何模型，对最短时间路径问题通过建立非线性规划模型，有效地解决了转弯半径、圆弧圆心位置和行走时间等问题。

关键词：机器人避障；最短路径；Dijkstra算法；几何模型；非线性规划模型1 引言随着科学技术的进步和计算机技术的发展，机器人的应用越来越广泛，在机器人的应用中如何使机器人在其工作范围内为完成一项特定的任务寻找一条安全高效的行走路径，是人工智能领域的一个重要问题。

本文主要针对在一个场景中的各种静态障碍物，研究机器人绕过障碍物到达指定目的地的最短路径问题和最短时间问题。

本文以2012年“高教社”杯全国大学生数学建模竞赛D题“机器人避障问题”为例进行研究。

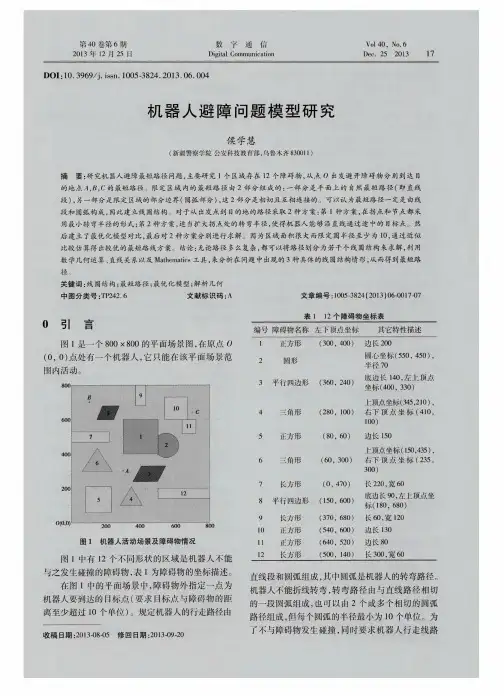
假设机器人的工作范围为800×800的平面正方形区域（如图1），其中有12个不同形状的静态障碍物，障碍物的数学描述（如表1）：图1 800×800平面场景图表1在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动，机器人不能与障碍物发生碰撞，障碍物外指定一点为机器人要到达的目标点。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为50=v 个单位/秒。

机器人转弯时，最大转弯速度为21.0100e1)(ρρ-+==v v v （ρ是转弯半径）。

如果超过该速度，机器人将发生侧翻，无法完成行走。

场景图中有4个目标点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，下面我们将研究机器人从O(0, 0)出发，求O→A、O→B、O→C和O→A→B→C→O的最短路径，以及机器人从O(0, 0)出发，到达A的最短时间路径问题。

机器人避障算法研究随着科技的迅猛发展，机器人已经成为了人类生活中不可或缺的一部分。

它们可以为我们执行一些重复性、危险或者需要高精度要求的任务，让我们的生活更方便、更安全，甚至可以帮助我们完成一些环境过于恶劣或者人类无法完成的工作。

但是，机器人在处理任务的过程中会遇到各种各样的问题。

其中，避障就是一个非常重要的问题。

为了让机器人在执行任务的时候可以自主寻路，我们需要对避障算法进行深入研究和探讨。

一、避障算法的分类机器人避障算法可以分为传感器型、图像型和机器学习型三种类型，每种类型算法都有其优势和适用场景。

1. 传感器型避障算法传感器型避障算法主要是通过机器人上搭载的传感器进行障碍物检测和距离计算，根据传感器的测量结果来进行路径规划和避障。

传感器常见的类型有超声波、激光雷达、红外线等。

由于传感器的精度和响应速度较高，因此传感器型避障算法被广泛应用于工业自动化和机器人导航。

2. 图像型避障算法图像型避障算法通过使用摄像头或者深度相机等设备，对机器人周围的环境进行视觉识别和分析，从而判断地面的地形、避开障碍物、规划最佳路径。

这种算法广泛应用于无人驾驶、智能家居、商业物流等领域，尤其是在机器人越野、复杂环境下的移动中，图像型避障算法的应用尤为突出。

3. 机器学习型避障算法机器学习型避障算法是最近几年出现的一种算法，它利用深度学习和强化学习等机器学习技术，通过机器自主学习周围环境和历史经验，从而进行障碍物检测和路径规划。

这种算法广泛应用于智能家居、医疗机器人、智能农业等领域。

二、机器人避障算法的研究进展机器人避障算法的研究已经有了很大的进展。

近年来，人们在机器人避障方面取得了很多成果，例如：1. 激光雷达技术的应用激光雷达是机器人避障中应用最为广泛的传感器之一。

激光雷达可以高精度地检测物体的距离和位置，在避障算法中扮演着非常重要的角色。

近年来，人们得到的最突出的成就之一是开发了具有高精度激光雷达的移动机器人系统，这些系统可以在大型仓库等环境中自主运行，从而提高了运行效率。

D題：机器人避障问題本文就机器人避强冋題，建立了相应的优化模里。

模1-：关干Hl器人从区域中一点到达另一贞的遐障最短路径的问题。

首先，题恿，师出HI器人行走的可行区域与危险区域；其次，在证明了具有園形限定区域的最皱路径间题为根据的前提下，可以得岀最短路径一定是由直线和闊弘组成，并依此建立了线岡结沟，将路径则分为若干个逆种线圆结构来求辭最短路径通用模型；最后，根弼最姬路径通用模型，采用穷举法把可能路径的最短路径列举出来，通il比较最终得出各种最短路径的坐标及总路程8UT：(1 ) 0-A的最矯路程为：471.04个单位(2) O T B的最短路程为:853.71个单位(3 ) 0->C的最短路程1088.20个单位(4 ) O T A—B T C T O的最短路径为：2730.01个单E模塑二：关于机器人UEM中一点到这另一点的避障最類时间路径的间题。

首先，根锯題意,找出公共切点，得出转弯时最大圆和最小圆的圆心坐标,确定冏心的变化X 围；其次，依擴圆心的变ItX围，得出转弯半径的变化X围；然后，利用MATLAB^件编程来求解最姬时间路径通用模型；最后，根据最短时间路径通用模里，得出所有结果，通过比较最终得岀机最后,我『1对模型进行了改进、检验、评价与推广。

关键词：优化模型最短路程线圆结构最短时间穷举法1问題重述1.1背景资料图1是一个800x800的平面场景图,在原点0(0,0)点处有一个机器人，它只能在该平面场景X围内活动。

图中有12f不同形状的区域是机器人不能与之发生磁撞的障碍物，障1.2 息(1)在图1的平面场景中，障碍物外荷定一点为机器人要到这的目标点。

现定机器人的行走路径由直筑段和冏弧组成，其中冏弧是机器人转弯路径。

(2)机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弘组成，也可以由两个或多个相切的凰聲路径组成，但毎个圆聲的半径最小为10个单也。

(3)HI器人直线行走的最大速度为v0 = 5个单位/秒。

机器人避障问题摘要移动机器人是一种能够在工作环境中自由移动并完成预定任务的智能系统，移动机器人的避障问题则是移动机器人控制领域的研究热点。

本文针对移动机器人的避障问题，建立了最短路径及最短时间路径的数学模型。

并应用于解决本题给定的路径规划问题，获得了满足问题需求的全部最优路径。

对于最短路径问题，本文分析了障碍物对移动机器人运行的影响，给出了最优移动规则；建立了简化的路径网格模型，将其抽象为由节点及边构成的两维图，并确定了其各项参数，再使用经典的Dijkstra算法获得可行的最短路径。

由于计算机行走过程与障碍物之间还需满足一定的间隔约束，故上述结果可能并非最优，故我们实际还需对次优的几条参考路径（也可通过以上Dijkstra算法获取）进行精算，经准确计算获得各段路径的具体位置后，确定实际的最短路径。

为方便计算，文中推导了自指定点向指定圆作切线，两个相离圆的内、外切线方程的解析表达式，给出了闭式结果，作为MATLAB编程的依据，从而大大提高了运算处理的速度及精度。

考虑到移动机器人需完成由O→A→B→C→O的多点移动，且中间不能折线运行，即机器人在通过上述点时一般必须以圆弧通过，且其上下游多数也是圆弧路径，其通过点并不固定。

为此，理论推导了该未知圆弧的约束公式，以各圆心之间距离最小作为优化条件，建立数学模型，再使用MATLAB中的fmincon有约束优化工具箱获得了理想的结果。

对于最短时间路径问题，本文分析了移动机器人弯道运行的速度曲线，特别是对O→A两点间的避障问题进行了详细的理论分析与推导，通过几何关系得出了转弯半径与总的移动距离、移动时间的严格数学关系，此后借助MATLAB优化函数fminsearch获得最佳的转弯半径。

经分析计算，得到下述结果：结论1：机器人完成O→A，O→B，O→C及O→A→B→C→O的最短路径总距离分别是：471.04、853.70、1050.50、2712.68单位长度；总时间分别是96.02、179.07、235.19及570.36秒。

机器人避障问题摘要：当今科学技术日益发达，高科技产品尤其是机器人在我们日常生活中运用的越来越广泛，它能够代替人类完成许许多多的工作，但如何能让机器人自动化的完成人类交给的任务成为设计机器人的关键。

我们做此题就是为了更好的利用机器人为我们提供方便，提高生活质量，若机器人程序设计不当不仅不会给人类带来方便，还很有可能给我们的生活带来更多的麻烦。

本题中提出了如何让机器人能够自动识别障碍物，保证机器人能够在合理区域行走，并设计出如何能让机器人自动判断最短路程于最短时间下行走路线的问题。

所以解决好本题可以为我们的生活提供帮助。

本文通过运用两点之间直线最短理论，优化问题，最短路问题，图论，以及运用matlab软件编程及作图的方法，阐述了机器人避障问题的相对优化方案的解决办法，即“两点之间直线最好，转弯半径最小”的理论，通过计算中的比较与选择把四条最短路径都求出了相对最优解，论证了转弯速度不会随着r的增加一直增大或减小，而是有一个最小极点的思想。

从而求出了r，以及最短的时间。

问题一，通过对最短路问题的分析，我们很容易分解成线圆结构来求解，然后把可能路径的最短路径采用穷举法列举出来，最终得出最短路径：O →A 最短路径为：471.0372O →B 最短路径为：838.0466O →C 最短路径为：1085.7531O→A→B→C→O最短路径为：2834.6591问题二，通过建立时间t与r的关系式，得出r在11.504时，从O到A的时间相对最短，最短时间为98.606004。

我们可以利用此篇论文解决生活中实际的问题，在计算时可以节省大量的时间，使机器人又准确又完善的完成我们给定的任务，从而进行拓展，给定区域内任何两个点，我们都可求出其最短路径和走完全程的最快时间。

从而可以让机器人帮助我们给家里打扫卫生或设计自动吸尘器等，也可使机器人在最短的时间完成工作，提高效率，延长机器人的使用寿命。

关键字：最短路问题优化问题 matlab一 问题重述 随着现代科学技术日新月异的发展，机器人越来越多的出现在日常生活中,它既可以通过运行预先编排的程序为人类服务，根据人工智能程序自动处理一些生活中问题，进而协助或者相应地取代人类的工作，可以说机器人的创新与改进正一步步影响着人类的发展。

D题机器人避障问题摘要本文综合运用分析法、图论方法、非线性规划方法，讨论了机器人避障最短路径和最短时间路径求解问题。

针对问题一，首先，通过分析，建立了靠近障碍物顶点处转弯得到的路径最短、转弯时圆弧的半径最小时和转弯圆弧的圆心为障碍物的顶点时路径最短、转弯在中间目标点附近时，中间目标点位于弧段中点有最短路径的三个原理，基于三个原理，其次对模型进行变换，对障碍物进行加工，扩充为符合条件的新的区域并在转弯处圆角化构成障碍图，并通过扩充的跨立实验，得到切线和圆弧是否在可避障区的算法，第三，计算起点、中间目标点和最终目标点和各圆弧及圆弧之间的所有可避障切线和圆弧路径，最后给这些定点赋一个等于切线长度或弧度的权值构成一个网络图，然后利用Dijkstra算法求出了O-A、O-B，O-C的最短路径为O-A：471.0372个单位，O-B：853.7001个单位，O-C：1086.0677个单位；对于需要经中间目标点的路径，可运用启发规则分别以相邻的目标点作为起点和终点计算，确定路径的大致情况，在进一步调整可得到O-A-B-C-O的最短路径为2748.699个单位。

针对问题二，主要研究的是由出发点到达目标点A点的最短时间路径，我们在第一问的基础上考虑路径尽可能短且圆弧转弯时的圆弧尽量靠近障碍物的顶点，即确定了圆弧半径最小时的圆弧内切于要确定的圆弧时存在最小时间路径，建立以总时间最短为目标函数，采用非线性规划模型通过Matlab编程求解出最短时间路径为最短时间路程为472.4822个单位，其中圆弧的圆心坐标为(81.430,209.41)，最短时间为94.3332秒。

圆弧两切点的坐标分别为（70.88,212.92）、（77.66,219.87）。

关键字：Dijkstra算法跨立实验分析法非线性规划模型一.问题的重述图是一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：日期：年月日编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：赛区评阅记录（可供赛区评阅时使用）：评阅人评分备注全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：机器人避障问题摘要针对题中机器人避障最短路径问题，文章使用简化后建立的最短路径的数学模型来解决此类问题。

对于问题1，我们matlab中自带函数graphshortestpath函数求解最短路径的数学模型。

其主要思想是：首先先证明出两点之间的最短路径是由两条线段和以中间点为圆心的圆的一段圆弧组成，然后证明圆弧的半径为定值10。

然后对模型简化使模型化为标准的最短路径模型，最后用graphshortestpath函数对模型求解。

针对问题2，我们建立了优化模型。

在问题1的基础上，我们对两种行走方案进行分析，根据转弯弧的半径变化对速度的影响我们锁定到一条路径，然后利用lingo对优化模型进行求解。

关键词：graphshortestpath函数、最短路径、避障问题1、问题重述已知：在下图中原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

机器人避障数学建模
机器人避障的数学建模通常涉及到使用传感器获取环境信息，通过算法处理这些信息，使得机器人能够避开障碍物。

以下是一个简化的数学建模示例：
1.坐标表示：用\((x,y)\)表示机器人在平面上的位置。

2.障碍物表示：用\((x_o,y_o)\)表示障碍物的位置。

3.距离计算：使用欧几里得距离或其他距离度量方法，计算机器人与障碍物之间的距离。

\[d=\sqrt{(x-x_o)^2+(y-y_o)^2}\]
4.避障算法：根据距离和传感器信息，制定避障算法。

例如，可以采用简单的规避方式，如果检测到障碍物在一定范围内，机器人就执行避障动作。

5.路径规划：考虑机器人的目标位置，通过路径规划算法（如A*算法）计算机器人避开障碍物的最优路径。

6.实时更新：在机器人移动的过程中，持续使用传感器获取新的环境信息，实时更新机器人的位置和障碍物的位置，以保持避障的准确性。

这只是一个简单的示例，实际的机器人避障数学建模可能涉及更复杂的算法和传感器数据处理。

在实际应用中，常见的传感器包括激光雷达、超声波传感器、摄像头等。

机器人避障问题摘要本文研究了在已知区域障碍物分布的情况下，机器人从起点到目标点避障最短路径或最短时间路径的问题，路径必须是由圆弧和与之相切的直线段组成的线圆结构。

一开始先对模型预处理，将所有障碍物外扩10个单位长度，划定危险区域，得到障碍扩展图。

针对问题一，经过分析论证，无论起点到目标点间危险区域有多少，最短路径都应该是紧绕危险点的切线圆路径，且可根据需依次绕过的危险点情况划分为N条子路径（见图5.1.2）求解，圆弧段取允许最小转弯半径。

模型求解分两步走：一、将实际障碍图转化为加权可视图，利用Dijstra算法搜索出在可视图下的最短路径，主要是找到必须绕过的若干危险点。

二、根据障碍扩展图将可视图中的路径修正为实际情况下的切线圆路径，求出最终结果。

在求解过程中运用MATLAB数学软件给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心连接两条切线，使机器人总的行走时间最短。

而圆弧可以有圆心坐标和半径唯一确定。

由此构建机器人行走总时间的目标函数，将机器人不与障碍物碰撞作为约束条件，将该问题转变为一个非线性规划问题，借助matlab求得最优解为:T=94.3314s。

关键词：路径规划最优化模型切线圆路径 Dijstra算法非线性规划matlab求解一、问题重述图1是一个800×800的平面场景图，在原点O(0,0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为50=v 个单位/秒。

机器人避障问题摘要本文主要研究两个方面的问题，问题一提出在一个固定的区域内有不同形状的障碍物12个，让机器人至少与障碍物保持10个单位的距离情况下，同时机器人还不能走折线，求最短路程问题，这个问题我们首先考虑了两个理论，在起点和终点之间有一障碍物，我们在障碍物的顶点做一个圆弧作为机器人的转弯路径，那么通过证明可知最短路径为起点到终点拉一绳子，当绳子处于最紧绷状态的路径。

这时路径即为起点,终点分别到圆弧的两段切线与中间弧度之和。

其次考虑所做圆弧的半径为最小转弯半径时这时所形成的路径最短。

结合以上理论，易得到最短路径分别为：A O → 471.05，B O →811.54，C O →1017.25，→O O C B A →→→2534.86。

问题二中,题目要求从A O →的最短时间路径，由于机器人走直线的速度为5=v ，而走转弯路径的速度是与转弯半径的长度有关，根据这些要求，我们过障碍物的右下顶点往左上顶点做对角线，并向左上顶点做10单位的距离，那么我们就在这条线上取一点作为圆弧的中心，然后构造一个目标函数求出最短时间路径，5)10(15)10(lim 22)10(1.010222R b er R a t R +-++++-=+-θ，得到02.96min =T 。

关键词：最短路径 线圆结构 解析几何 最短时间一、问题重述在800800⨯的平面场景图中，在原点O 有一机器人，它只能在平面场景中活 动，且不能碰撞场景图中不同形状的障碍物，且机器人所行走的路径与障碍物的距离至少超过10单位。

规定机器人的行走路径由直线和圆弧组成，其中圆弧是机器人的转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由多个相切的圆弧路径组成，但每个圆弧的最小半径为10个单位。

为了能到达目的地，机器人的行走路径与障碍物的最近距离为10个单位，否则发生碰撞则不能完成行走。

机器人直线行走的最大速度为秒。

个单位/50=V 机器人转弯时，最大转弯路径为21.01001)(ρρ-+==V V V ,其中。

关于机器人避障行走问题的研究摘要本课题主要研究机器人避障行走问题，机器人行走过程，需躲避障碍物区域且保证所经路径按直线段和圆弧进行行走。

依据题目要求最短路径和最短时间路径目标，运用穷举法，先绘制出可能是最短路径的行走路线。

然后，利用平面解析几何知识，求解各路线长度并进行比较，找出最短路径。

最后，引入机器人速度数据，建立数学模型，求解出最短时间路径。

问题一、根据题目限定的机器人和障碍物之间10个单位的距离要求，先绘制出机器人能够行走的活动区域。

然后，利用平面几何知识，列出线段与圆弧结构下的行走路程关于圆弧半径的函数关系式。

运用求导法则对所列函数关系式进行求导，得出结论：只有当圆弧半径最小时（最小半径为10），才能使线弧结构的路程达到最小。

依据所得结论，运用穷举法列出从原点出发到各个目标点的所有可能最短路径。

分别进行求解并互相比较，最终得出机器人行走到不同目标点的最短路径为：O→A：471.0372；O→B：853.702132；O→C：1053.140；O→A→B→C→O：2707.4379。

（注：路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标，可通过将坐标点设定成未知量，列函数方程组编写LINGO程序进行求解得出。

起点、终点及圆弧圆心的具体坐标，见各路径模型求解部分所列坐标表格。

）问题二、路线制定过程中，引入机器人直线速度和转弯速度数据。

以行走到目标点A花费时间最短为目标建立优化模型。

根据模型，编写LINGO程序，求解出最短时间路径下，机器人过点A的圆弧圆心为（82.04274,210），圆弧半径为10.97436，花费的最短时间为94.34632。

关键词：穷举法求导法则平面几何优化模型最短时间路径1问题重述1.1问题背景进入科技时代以来，随着信息技术的不断发展，机器人自动化研究越来越成为人们关注的重点，机器人避障行走问题也成为机器人程序设定的一个常见问题。

而路线制定过程中，行走线路制定方法的研究和精确坐标数据的计算是必不可少的，且对今后机器人行进程序的设定具有很好的参考价值。

第九届“挑战杯”甘肃省大学生课外学术科技作品竞赛参赛人员：xxx xxxxxx指导老师：xxx xx定西师范高等专科学校数学系机器人避障问题的优化模型建立与分析（定西师范高等专科学校数学系，指导老师：xxx x x）【摘要】本文针对机器人避障布置问题，从不同角度出发，以最短路径和最短时间路径为目标函数，建立了多个优化模型。

做出了满足条件的机器人绕过障碍物行走的最短路径，并对A、B、C处各点所在圆弧的圆心的确定进行了详细的模型分析；通过建立方程模型，分析计算了机器人从O出发到达A点，机器人在圆弧路径上行走时对应的圆心位置，并研究了该圆心位置在一定的范围内变化对时间的影响，确定了机器人行走的最短时间路径。

针对问题一，先根据问题情况进行分类分析，一类是O-A,O-B,O-C两点之间用直线和圆弧光滑连接，可利用Autocad软件直接作图；另一类是经过中间点的连线O-A-B-C-O,需对各个中间点处的圆弧位置作分析推理，找出使路径最短的圆弧圆心。

然后根据已有数据，充分利用Autocad软件的切点捕捉及标注功能等进行切线和圆弧作图、各条路径的线性标注和圆弧标注，再根据标注值对各路径上切线长和弧长求和并比较大小，选择出避障的最短路径。

并对路径的各点建立模型，运用Mathematica软件求解，确定过各点的圆弧的圆心坐标，求解满足给定条件的机器人绕过障碍物行走的最短路径。

针对问题二，在保证障碍物顶点离圆弧最近（10个单位）的前提下利用Mathematica 软件, 建模求解弧半径-时间函数，确定圆弧圆心和半径，并用Autocad作图、标注，通过计算推出机器人从O出发，到达A的行走最短时间路径。

【关键词】最短路径优化模型避障 Autocad软件 Mathematica软件一、问题重述图1是一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述如下表：在图1的平面场景中，障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过10个单位）。

机器人障碍问题摘要本文研究了有若干障碍物的平面场景中，机器人避障行走的最短路径以及最短时间路径的问题。

针对问题一，首先给出简单证明了两个对称点绕过圆形障碍物的最短路径为两条与圆形障碍物相切的直线，加上两切点间的劣弧。

然后分了四种情况，分别给出了不同直线与圆相切时，根据各已知点坐标，求相应切点、直行路径及劣弧长度的方法。

然后在满足机器人从定点(0,0)O出发绕过障碍物，距离障碍物至少超过10个单位，不能折线转弯绕过障碍物的条件下，以前面的证明为依据，将机器人行走路径设计为由直线和圆弧组成。

针对不同的起点和终点，将总路径分解为上述四种情况，利用MATLAB6.5.1，分别求出相应的切点及各转弯圆的劣弧长，最后比较得到相对较短的行走路径。

并根据机器人在不同路径上的速度的不同，求出避障前进的最短路径时所需要的行走时间。

具体如下：→的最短路径为471.0375个单位，所需的时间为96.0177秒O A→的最短路径为812.7029个单位，所需的时间为170.5132秒O B→的最短路径为：1090.8个单位，所需的时间为222.9373秒O C→→→→的最短路径为：3137.8个单位，所需的时间为652秒。

O A B C O针对问题二，要求求出机器人从(0,0)O出发，到达A的最短时间路径。

因为机器人行走路径为直线时的速度为定值，弧线行走的速度与弧所在的圆半径有关，由此得到行走时间与圆弧半径ρ的关系式，利用高等数学的极值定理条件，估算出ρ=11.5052个单位时从O A→所需时间最短，为95.1328秒。

该模型简单、便于理解，理论性较强。

另外图形的使用，使问题更加清晰。

该模型还可用于求解设计最优路线问题。

关键词最短路径圆弧半径最短时间切点一 问题重述在一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

平面场景中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物。