悬链线方程及曲线弧长

之阳早格格创做常常所有资料包罗导线正在内，皆具备一定的刚刚性，但是由于悬挂正在杆塔上的一档导线相对付较少，果此导线资料的刚刚性对付其几许形状的效率很小，故正在估计中假定：（1）导线为理念的柔索.果此，导线只启受轴背弛力（或者推力），任性一面的直矩为整.那样导线力教估计可应用表里力教中的柔索表里举止估计.（2）效率正在导线上的荷载均指共一目标，且沿导线匀称分散.一、悬链线圆程及直线弧少为了分解便当，咱们先从悬挂面等下，即相邻杆塔导线悬挂面无下好的情况计划导线的应力及几许闭系.本量上，导线悬正在空中的直线形态，从数教角度用什么圆程去形貌是举止导线力教分解的前题.由于假定视导线为柔索，则可依照表里力教中的悬链线闭系去举止分解，将要导线架设正在空中的几许形态视为悬链形态，而由此导出的圆程式为悬链线圆程.如图2－5所示，给出了悬挂于A、B二面间的一档导线，假定为悬挂面等下的孤坐档，设以导线的最矮面O面为本面修坐直角坐标系.图2-5导线悬链线及坐标系共时假定导线牢固正在导线地圆的仄里，可随导线所有晃动，隐然那是一个仄里力系.根据那个坐标举止导线的受力分解，可修坐导线的悬链线圆程.咱们先从局部受力分解启初，再找出其普遍顺序.最先正在导线上任与一面D（x,y），而后分解OD段导线的受力闭系，由图2－5所示，此OD段导线受三个力而脆持仄稳，其中D面启受推力为T x=σx S，它与导线直线相切，与x轴夹角为α； O面启受推力为T0=σ0S，T0为导线O面的切线目标，恰与x轴仄止，故又称火仄弛力；别的另有OD 段导线自己的荷载为G=gSL x，其中L x为OD段导线的弧少.将OD段导线的受力闭系绘为一个三角形表示，如图2－6所示，图2-6导线受力情况由静力教仄稳条件可知，正在仄里坐标系中，其火仄分力，笔直分力的代数战分别等于整.或者沿x轴或者y轴上分力代数战分别等于整.笔直目标分力G=T x sinα=gSL x;火仄目标分为T0=T x cosα=σ0S.其中σ0、T0为导线最矮面的应力战弛力，σx、T x为导线任一面的应力战弛力，S、g为导线截里战比载.将上述二式相比，则可供得导线任性一面D的斜率为：(2-10)由微分教知识可知，直线上任一面的导数即为切线的斜率.式（2－10）是悬链直线的微分圆程.咱们要用坐标闭系表示出导线受力的普遍顺序，还需要将没有定量L x消去，果此，将式对付x微分得：（微分教中弧少微分公式为dS2=(dx)2+(dy)2）将上式移项整治后，二端举止积分那是个隐函数，果此，再举止分散变量积分，查积分公式有：（2－11）再举止分散变量积分，有于是，导线任一面D的纵坐标为：（2－12）式（2－12）是悬链圆程的一般形式，其中C1战C2为积分常数，其值可根据与坐标本面的位子及初初条件而定.如果将坐标本面于导线最矮面处，则有下述初初条件：x=0, dy/dx=tgα=0代进式（2－11）则C1＝0，将x=0,y=0,C1＝ 0 代进式（2－12），，如许，供得坐标本面最矮面O处的悬链圆程为：（2－13）式中σ0—火仄应力(即导线最矮面应力)，MPa;2.当坐标本面选正在其余面（比圆选正在悬挂面处）时，悬链线圆程的常数项将有所分歧，不妨得到分歧的公式.若式（2－13）中x代表档距的时间，则y即为导线的弧垂，果此悬链线圆程形貌了导线弧垂与应力、比载及档距之间的基础闭系，此式称为透彻式.本量上导线的悬链线圆程还不妨从另一种办法举止推导,底下介绍如下：由式,对付其供导得：变更为,为找本函数举止积分,由积分式二边积分，则有：形成指数形式为那是个隐函数，为解出，对付应有式：将二式相减则有：果为单直正弦函数为：单直余弦函数为：又果为：末尾积分有：定积分常数,果正在坐标本面则，其截止是一般的，即正在线路安排中，为了估计上的便当，普遍没有使用透彻式圆程，而是将其展启为泰勒级数形式.将悬链线圆程式（2－13）展启成无贫级数（正在x=0面），可得：（2－14）2．直线弧少（或者弧少圆程）导线最矮面O至任一面的直线少度喊干弧少，用Lx表示.将式（2－11）代进式（2－10）中，且积分常数C1＝0，得导线的弧少圆程为（2－15）根据式（2－15）不妨估计一个档距内导线的直线少度（也喊一档线少）将弧少圆程式（2－15）展启成无贫级数可得：（2－16）一品量匀称分散的绳二端悬挂时绳子所表示的直线为悬链线.闭于悬链线剖析圆程的供解，尔很早便知讲其圆程为单直余弦函数.然而当时数教火仄尚已谦脚央供.厥后教会闭于单直函数的相闭真量后，又由于脆疑绳中弛力到处相等而推出悖论，本钻研便此停顿.直到7月初，尔又念起了该直线的圆程供解问题.需要证明的一面是，绳中弛力到处相等央供绳子无品量、绷紧，对付于悬链隐然没有适用.但是受力目标沿着绳是透彻的，所以必须分散力的目标去供解.假设一个无限少的品量匀称分散的绳子正在沉力效率下自然下垂.设绳底端受到推力为T0，线稀度为ρ，沉力加速度g.如图所示修坐直角坐标系，设绳对付应的函数为y=f(x)对付于横坐标从0至x那一段的绳，设品量为m，少度L，受沉力为G，受顶端推力大小为T，该力倾斜角为θ该段绳受三力仄稳：T、G、T0，绘出受力示企图，有G/T0=tanθ由导数的几许意思，tanθ=dy/dx，而G=mg=ρgL，故ρgL/T0=dy/dx，ρgL=T0*dy/dx对付上式与微分，得ρg*dL=T0*d2y/dx，而dL=(dx2+dy2)1/2=[1+(dy/dx)2]1/2*dx，代进得ρg[1+(dy/dx)2]1/2=T0*d2y/dx2=T0*d(dy/dx)/dx，令dy/dx=P，则ρg(1+P2)1/2=T0*dP/dx，ρg/T0*dx=dP/(1+P2)1/2对付二侧与积分得∫ρg/T0*dx=∫dP/(1+P2)1/2ρgx/T0=sinh-1P+C1，P=sinh(ρgx/T0-C1)，dy/dx=sinh(ρgx/T0-C1)当x=0时，dy/dx=0，代进得sinh(-C1)=0,C1=0，故dy=sinh(ρgx/T0)*dx再次积分，得y=T0/ρg*cosh(ρgx/T0)+C2当x=0时，y=0，故0=T0/ρg*cosh0+C2,C2=-T0/ρg设k=T0/ρg，则y=kcosh(x/k)-k，若只思量其形状可忽略常数项，故悬链线圆程为y=kcosh(x/k)-k，其中k=T0/ρg闭于单直函数的一些证明：单直正弦函数sinhx=(e x-e-x)/2，单直余弦函数coshx=(e x+e-x)/2由其定义可得d(sinhx)/dx=coshx，d(coshx)/dx=sinhx，cosh2x-sinh2x=1其反函数分别为反单直正弦函数sinh-1x=ln[x+(x2+1)1/2]，反单直余弦函数cosh-1x=ln[x+(x2-1)1/2]波及的一步积分：正在∫dP/(1+P2)1/2中，令P=sinht∫dP/(1+P2)1/2=∫d(sinht)/(1+sinh2t)1/2=∫cosht*dt/cosht=∫dt=t+C=si nh-1P+C。

在高压架空线路的设计中，不同气象条件下架空线的弧垂、应力、和线长占有十分重要的位置，是输电线路力学研究的主要内容。

这是因为架空线的弧垂和应力直接影响着线路的正常安全运行，而架空线线长微小的变化和误差都会引起弧垂和应力相当大的改变。

设计弧垂小，架空线的拉应力就大，振动现象加剧，安全系数减少，同时杆塔荷载增大因而要求强度提高。

设计弧垂过大，满足对地距离所需杆塔高度增加，线路投资增大，而且架空线的风摆、舞动和跳跃会造成线路停电事故，若加大塔头尺寸，必然会使投资再度提高。

因此设计合适的弧垂是十分重要的。

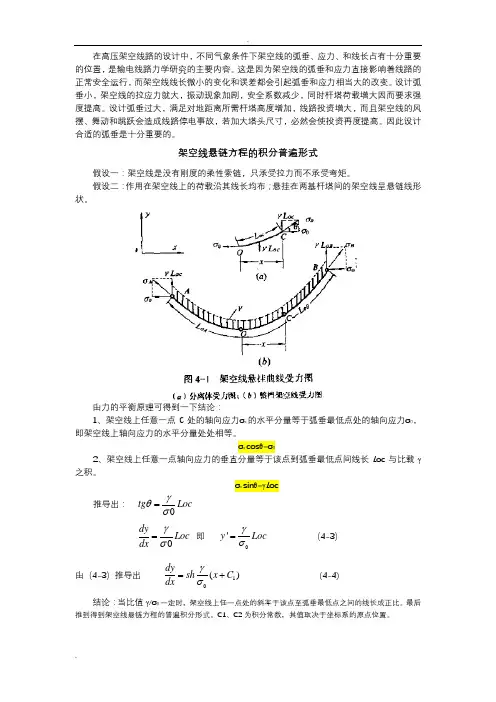
架空线悬链方程的积分普遍形式假设一：架空线是没有刚度的柔性索链，只承受拉力而不承受弯矩。

假设二：作用在架空线上的荷载沿其线长均布；悬挂在两基杆塔间的架空线呈悬链线形状。

由力的平衡原理可得到一下结论：1、架空线上任意一点C 处的轴向应力σx 的水平分量等于弧垂最低点处的轴向应力σ0，即架空线上轴向应力的水平分量处处相等。

σx cos θ=σ02、架空线上任意一点轴向应力的垂直分量等于该点到弧垂最低点间线长L oc 与比载γ之积。

σx sin θ=γL oc推导出： 0tg Loc γθσ=dy Loc dx γσ= 即 0'y Loc γσ= （4-3） 由（4-3）推导出10()dy sh x C dx γσ=+ (4-4) 结论：当比值γ/σ0一定时，架空线上任一点处的斜率于该点至弧垂最低点之间的线长成正比。

最后推到得到架空线悬链方程的普遍积分形式。

C1、C2为积分常数，其值取决于坐标系的原点位置。

0(1)20y ch x C C σγγσ=++ （4-5）等高悬点架空线的弧垂、线长和应力等高悬点架空线的悬链方程等高悬点是指架空线的两个挂点高度相同。

由于对称性，等高悬点架空线的弧垂最低点位于档距中央，将坐标原点取在该点，如图：0(1)0y ch x σγγσ=- （4-6） 由上式可以看出，架空线的悬链线具体形状完全由比值σ0 /γ决定，即无论何种架空线、何种气象条件。

•பைடு நூலகம்
A M0
•Mn1
•
B Mn
MnB,依次用弦将 O
x
相邻两点联结起来, 得到一条内接折线. 记每条弦
的长度为 |M i 1 M i|i , 1 , 2 , ,n ,令 m 1 i n|M ai 1 x M i|.
如果当分点无限增加, 且 0时 ,折线长度的极限
n
lim |
0 i1
Mi1Mi |存在 ,则称此极限为曲线弧
弧长元素为 ds(dx)2(dy)2 r2()r2()d
弧长 s r 2( ) r2( )d .
史上最详细的平面曲线的弧长公式计算(微
9
积分)
7.4 平面曲线的弧长
s r 2( ) r2( )d
例
求极坐标系下曲线
r
asin
3
的长.
3
(a0)(03π)
解
s
r2()r2()d
等于椭圆 y x c1o tas2sitn (0t2π)的周长.
证 设正弦线的弧长等于s1 对称性
π
s120
1y2dx2π 0
1a2co2xsdx
设椭圆的周长为s2
π
s220
(x)2(y)2dt2π 0
(st)i2 n(1a2)(c t)2d o t s
π
2
1a2co2td st
0
π
2
o ax xdxb x
任取小区间 [x,xdx],以对应小切线段的长代替小
弧段的长, 小切线段的长为:
(dx)2 (dy)2 1 y2dx
弧长元素 ds 1 y2dx, 弧长 s b
(弧微分)
a
史上最详细的平面曲线的弧长公式计算(微

他构造了微分方程 ： ＝ ， 中 是弧 长 ， 其 ｃ为有关参 数， 由此方程 可推知 曲线方程 为 ｙ
称为双 曲余弦 ， 它无论是在理论上还是在工程技术上 ， 都是一条重要的 ｍ线 。有人说 ， 条项链 上悬挂 着一个 神奇的数 ， １ 这 因为构成悬链线 曲 线方程 的主体 是 Ｐ。很 快 ， 雅各布 ・ 贝努里又证明了悬挂于两个 固定点 之间的 同一条项链 ， 在所有可能 的形 状中 ， 以悬链线 的重心最低 ， 因而 也 就具有最小位能 。这个发现启示 了一 个深刻 的现象 ： 在大 自然 的神 秘 布局 中总是按 最小 原理行 事， 这也体 现在悬链线 的另一个性质上 ： 以 悬链线为母线旋转而成的旋转体的表面积最小。仔 细观察小孩 吹的肥 皂泡 ， 介于两个平行圆面之间的肥皂膜就是南一条悬链 线旋 转而成的 ， 正是因为悬链 线的这 一特性 ， 肥皂泡 的表面张力最小 ， 而呈现 出美 使 从 丽梦幻般的形状。法国著名的昆虫 学家法 布尔在 《 昆虫记》 中写道 ： 每 “ 当地心引力和扰性同时发生作用时 ， 悬链 线就出现了 ， 这就是一条软绳 子 两 端 抓 住 而 垂 下 来 的 形状 ， 就 是 被 风 吹 起 来 船 帆外 形 的 形 这
科技信息
从达 ・ 芬奇的问题到一条善名硇曲线
华北 电力 大学数 理 系 柳 燕
Ｊ ■＝ 悬 链线 － ■。 昌 ：‘ Ｉ＝
［ 要］ 芬奇的问题给数学带来 了思索与研 究， 摘 达・ 贝努里和 莱布尼兹解决 了他的问题， 并将其理论广泛地应用于 实际中。 ［ 关键词 ］ 悬链线 双曲函数 拱桥 最小原理 达 － 奇不仅是意大利 的著名画家 ， 芬 他画 的《 蒙娜丽莎》 带给 了世界 永 恒的微笑 ， 而且他还是数学家 、 学家和机械工程 师 ， 物理 他学识 渊博 ， 多才多艺 ， 几乎在每个领域都有他的贡献 ， 他还是 数学上第 一个使 用加 减 符号的人 ， 他甚至认 为 ：在科学 上 ， “ 凡是用不 上数学 的地 方 ， 凡是 与 数学没有交融 的地方 ， 都是不可靠 的” 。他本人在创作 《 蒙娜丽莎》 ， 时 认 真地研究了主人公的心理 ， 做了各种精确的数学计算 ， 确定 人物的 来 比例结构 ， 以及半身人像 与背 景间关系 的构 图问题。当我们欣赏 着他 的《 抱银貂 的女人》 中脖颈上 悬挂 的黑色珍珠项链 时 ， 我们注意 的是项 链与女人相互映衬的美与光泽 ， 而不会像 达 ・ 芬奇那样去苦苦思索这样 个 问题 ： 固定项链的两端 ， 使其在重力 的作用 下 自然下垂 ， 么项链 那 所形成 的曲线是什么 ？这就 是著名的悬链线 问题 ， 他没有找到答 案就 去世 了。伽利 略也研究 过这个 问题 ， 他猜 想这条 曲线可 能是 抛物线 。 从外表上看 ， 悬链线 的确很像抛物线 ， 荷兰科学家惠更斯用物理的方法 证 明了这 条曲线不是抛物线 ， 到底是什么 ， 一时也求不 出来 ， 但 他 直到 几十年后 ， 雅各布 ・ 贝努里又重新提 出了这个问题 ， 这个问题 由约翰 ・ 贝 努里 （ 雅各布的弟弟 ） 与莱 布尼兹利用微 积分得以解决 。以下是 约翰 ・

索道缆绳长度的估算一．摘要：本文利用铁塔与铁塔间的距离以及铁塔与铁塔间的高度差的关系。

通过对该题的逐层分析以及现实生活中的观察，确定为每一小段缆绳可以近似看作是抛物线，因此可以建立抛物线的模型，根据所给数据以及抛物线的有关性质求出每一小段抛物线解析式2i i i y a x b x c =++，采用曲线弧长公式:id i l =⎰,从而求出每一小段缆绳的长度，最后求和得到缆绳的总长为80i i ll ==∑=1536.275m ，具体数据见表3。

通过查找相关资料，以及用数学知识联系实际问题，得出把每一小段缆绳看作抛物线具可行性。

关键词：缆绳的总长 抛物线 曲线弧长公式 对称性二．问题提出：山脚到山顶有一缆车索道，全长约1471m ，高差为380m ，采用循环单线式修建。

缆绳悬挂在上站到下站的里程中的8个铁塔上，这8个铁塔依山势走向而距离不等，从而到第一站的水平距离为0d ,高差为0h；从第一铁塔到第二铁塔的水平距离为1d ，高差为1h ，….，从而第八个铁塔到上站的水平距离为8d ，高差我8h ，具体数据如表1所示。

道工程所用的总长度。

三．问题的分析：由题意可知，目的是建立一种模型，来求得该景点整个索道工程的缆绳的总长度。

根据现实生活中的观察，缆绳的形状近似抛物线，因此可以建立抛物线模型，利用数据及抛物线的性质求出各抛物线的解析式，利用曲线弧长公式：id i l =⎰(1)计算出各弧长的长度，最后求和计算出缆绳的总长：8ii l l ==∑ (2)四. 建模过程：1模型假设(1)假设题目中给的数据可靠无误的(2)在该问题中，假设忽略缆绳实际形状与抛物线的差别，直接用抛物线近似求解。

(3)忽略缆绳下垂的最低的差别，假设下垂的最低点在两端铁塔最低塔顶的1m 处。

(4)假设忽略缆绳在铁塔上缠绕的长度2.符号说明表23.模型建立对于该题，关键是建立一种模型，求出缆绳的总长，要求使其误差尽可能的小，据实际观察缆绳的形状可近似地看成九段抛物线。

得到 y’与 x’的函数关系： 这显然是一条悬链线.证毕.
1
2x′
y = p + p sinh ( )
2
p
p
2x′
y = cosh ( )
2
p
图一（以抛物线为参照物，此为 p=1 时的特殊情况） 图二（以直线为参照物）
附录 以下为定积分(*)的计算过程：
x
x
1
1 + dx = x 1 +
−
p
p
p
悬链线与抛物线关系的证明
作者：cdlmnqust
定理 在一条直线上滚动的抛物线，其焦点的轨迹是一条悬链线. 证明 设坐标系内的抛物线方程为
x y = 2p 其焦点为
p F(0, )
2 我们采取转换参照物的方法，假定抛物线不动，则直线紧贴着抛物线旋转，此时的直 线是抛物线的切线（如图 1），设其切点为
切线的方程为
x P(x , 2p)
x
x
y = p (x − x ) + 2p
即
, 与 y 轴的交点为
x y=
x
−
x 2
p
x T(0, − 2p)
, 过 F 作切线 PT 的垂线 FQ 交 PT 于 Q,由抛物线的性质得 PF=FT，则 PT PQ = QT = 2 可求得
所以
x PT = x + p = 1 +
(px +
1
+
x p
)d(px)
1
+
x p
(px +
1
+
x p
)
x p (
+ 1)
d(px)

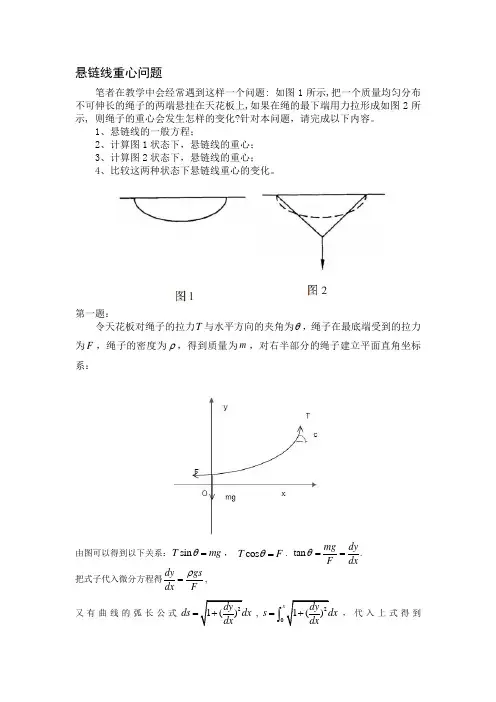
悬链线重心问题笔者在教学中会经常遇到这样一个问题: 如图1所示,把一个质量均匀分布不可伸长的绳子的两端悬挂在天花板上,如果在绳的最下端用力拉形成如图2所示, 则绳子的重心会发生怎样的变化?针对本问题，请完成以下内容。

1、悬链线的一般方程；2、计算图1状态下，悬链线的重心；3、计算图2状态下，悬链线的重心；4、比较这两种状态下悬链线重心的变化。

第一题：令天花板对绳子的拉力T 与水平方向的夹角为θ，绳子在最底端受到的拉力为F ，绳子的密度为ρ，得到质量为m ，对右半部分的绳子建立平面直角坐标系：由图可以得到以下关系：sin T mg θ=， cos T F θ=. tan mg dyF dxθ==. 把式子代入微分方程得dy gsdx Fρ=, 又有曲线的弧长公式21()dy ds dx dx =+,201()dys dx dx=+⎰，代入上式得到201()x dy gs dy dx dx F dxρ=+⎰. 设dy p dx =,上式可以转化成201x g p dx F ρρ=+⎰，则有2'1dp g p p dx Fρ==+, 分离变量并两边同时积分得：21dp gdx Fpρ=+⎰⎰积分可以得到：2ln(1)gp p x c Fρ++=+（其中c 为常量）当0x =时,0dyp dx==, 代入得0c =，整理式子得到22212gx gxFFp e pep ρρ+=-+.将上式整理得：1()2gx gxF F dy p e e dxρρ-=-=两边同时积分得：()2gxgxFFF y eegρρρ-=-令F a g ρ=,化简整理可以得到()2x xa aa y e e -=+所以悬链线的一般方程为()2x xaa a y e e -=+。

第二题：由上图可得，假如设两个悬点为),(),,(0000y x C y x B - ，则有222o y s a =+，悬链线的总长度为ax ashs 02=。

1 悬链线方程的推导 锚链一端受到水平预张力()0T KN ，并在其均匀分布的自重力作用下产生下垂。

设锚链水中 单位重力为()/W KN m ，建立如图1所示的直角坐标系，并设锚链曲线对应的函数为()y f x =。

对于横坐标上0至x 这段锚链，长度为L ，则G wL =，顶端拉力为T ，该力倾角为θ，水平张力0T ,根据力学原理可知，T ，G 和0T 三力平衡。

可知0tan /G T θ=(图2). 图1图2假定该水平张力在锚链上处处相等，对于任意一段锚链L ，该平衡均成立，0tan wL T θ=，而tan dy dxθ=，对该式取微分，则有()()00tan x w d d L T θ===（1） 弧长微分ds=1）分离变量后并积分： 0tan d w dx T =⎰（2） 对式（2）积分后得到：10tan w sh x c T θ⎛⎫=+ ⎪⎝⎭（3）对式（3）再次分离变量后，得10w dy sh x c dx T ⎛⎫=+ ⎪⎝⎭（4）并积分，10w y sh x c dx T ⎛⎫=+ ⎪⎝⎭⎰（5）查积分公式可得：0120T w y ch x c c w T ⎛⎫=++ ⎪⎝⎭（6） 式（6）即为锚链悬链线的一般方程。

假设锚链末端拖地，并设拖地点为原点，则对于拖地点有，0,0,tan 0x y θ===，代入式（3）和（6），联立方程后，可解得：10c =，2T c w=,代入式（6）得: 001T w y ch x w T ⎛⎫=- ⎪⎝⎭（7） 式（5）即为拖地点为原点的悬链线一般方程。

而对于悬挂点为原点的悬链线方程，仅系数有所变化，如下式表示，推导过程不再叙述。

该方程对于有悬锤的悬链线更适用。

0,0,tan wL x y Tθ===，代入式（3）,（6）可解得： 002cosh sinh wL T a T c w⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎣⎦=（8） 式（8）即是以悬挂点为原点的悬链线一般方程。

拟悬链线轨迹计算悬链线是一种特殊的曲线，它在重力影响下形成的曲线轨迹。

它经常应用于建筑设计、桥梁工程以及其他工程领域。

悬链线轨迹的计算是一个复杂的过程，需要使用微积分的知识和数值计算方法。

本文将详细介绍悬链线轨迹的计算过程。

首先，我们需要了解悬链线的定义和性质。

悬链线是指一条杆或绳在两端受到重力作用时的形态。

悬链线的形状取决于杆或绳的质量、长度和受力情况。

悬链线的性质包括：对称性、唯一性、可微性和平滑性。

悬链线的轨迹计算可以通过以下步骤进行：1.悬链线的微分方程悬链线可以通过一个微分方程来描述。

考虑杆或绳的长度为L，其一端坐标为(x,y)，可以得到微分方程：ds = sqrt(1 + (dy/dx)^2) dx其中，s表示曲线弧长。

2.边界条件悬链线的边界条件包括两端点坐标和斜率。

假设杆或绳的一端坐标为(x1,y1)，斜率为m1，另一端坐标为(x2,y2)，斜率为m2、则有以下边界条件：y(x1)=y1y'(x1)=m1y(x2)=y2y'(x2)=m23.轨迹计算方法根据边界条件和微分方程，我们可以采用数值计算方法求解悬链线的轨迹。

一种常用的方法是欧拉法，可以简单地理解为将微分方程离散化，然后沿着曲线逐步计算得到轨迹。

具体步骤如下：a) 将悬链线划分为若干小段，将弧长s离散化为ds。

b)选择一个合适的初始点，根据边界条件计算初始斜率值。

c)逐步计算离散点的坐标和斜率值，直到计算到终点。

4.数值计算方法欧拉法只是一种简单的数值计算方法，对于悬链线的轨迹计算有一定的误差。

为了提高计算的准确性和稳定性，可以采用更高阶的数值计算方法，如四阶龙格-库塔法。

此外，还可以使用数值计算软件来进行计算，如Matlab、Python等。

5.曲线参数化悬链线的轨迹计算得到的是一系列坐标点，为了便于进一步的分析和应用，可以对曲线进行参数化。

将弧长s作为参数，以x和y作为变量，可以得到参数方程：x=f(s)y=g(s)其中，f和g是参数方程的具体形式。

1 悬链线方程的推导 锚链一端受到水平预张力()0T KN ，并在其均匀分布的自重力作用下产生下垂。

设锚链水中单位重力为()/W KN m ，建立如图1所示的直角坐标系，并设锚链曲线对应的函数为()y f x =。

对于横坐标上0至x 这段锚链，长度为L ，则G wL =，顶端拉力为T ，该力倾角为θ，水平张力0T ,根据力学原理可知，T ，G 和0T 三力平衡。

可知0tan /G T θ=(图2).dy dx θ=，dy 10y T ⎝⎭查积分公式可得：0120T w y ch x c c w T ⎛⎫=++ ⎪⎝⎭（6） 式（6）即为锚链悬链线的一般方程。

假设锚链末端拖地，并设拖地点为原点，则对于拖地点有，0,0,tan 0x y θ===，代入式（3）和（6），联立方程后，可解得：10c =，2T c w=,代入式（6）得: 001T w y ch x w T ⎛⎫=- ⎪⎝⎭（7） 式（5）即为拖地点为原点的悬链线一般方程。

而对于悬挂点为原点的悬链线方程，仅系数有所变化，如下式表示，推导过程不再叙述。

该方程对于有悬锤的悬链线更适用。

0,0,tan wL x yθ===，代入式（3）,（6）可解得： c L 度L 21c 和2c 3式中；C G 为悬锤水下重力，实际重力应作换算。

()()1212000000cosh sinh sinh C C w L L G w L L G T a T a T T T w y ch x w T w w ++⎡⎤⎧⎫++⎡⎤⎢⎥⎪⎪⎢⎥⎪⎪⎣⎦⎢⎥=--⎨⎬⎢⎥⎪⎪⎢⎥⎪⎪⎣⎦⎩⎭（10） 以悬挂点为原点建立的悬链线方程，同样适用于锚链不拖地的情况，但悬链线方程式应通过试算来确定。

式（10）即为锚链悬挂点至悬锤处的悬链线方程：悬挂点坐标为,x a y b ==则悬挂点以下悬链线方程为：11000000cosh sinh sinh wL wL T a T a T T T w y ch x a b w T w w ⎧⎫⎡⎤⎡⎤⎛⎫⎛⎫⎪⎪⎢⎥ ⎪⎢⎥ ⎪⎪⎪⎝⎭⎝⎭⎣⎦⎢⎥=---+⎨⎬⎢⎥⎪⎪⎢⎥⎪⎪⎢⎥⎣⎦⎩⎭（11） 根据式（10）和（11），对于任意给定的x 坐标，可求出y 值，即可知任意位置的水深值。

悬链线长度计算（原创版）目录1.悬链线的定义与性质2.悬链线计算公式3.悬链线长度计算的实际应用4.悬链线长度计算的注意事项正文一、悬链线的定义与性质悬链线，又称悬链曲线，是一种在数学和物理学中常见的曲线。

它是由一条细长的弹性绳或链条，在自身重力作用下自由悬挂形成的曲线。

悬链线在自然界和工程领域中有着广泛的应用，例如桥梁建设、机械设计等。

悬链线具有如下性质：它是一种特殊的二次曲线，形状类似于一个倒悬的抛物线；悬链线的曲率是连续变化的，且在曲线的每个点上都有切线；悬链线是由一系列微小的直线段组成的，每一段直线段的两端都在同一高度上。

二、悬链线计算公式为了计算悬链线的长度，需要先了解悬链线的计算公式。

悬链线的计算公式为：L = (π/2) * (h^2 / g)^(1/3)其中，L 表示悬链线的长度；h 表示悬链线两端的高度差；g 表示重力加速度，一般取 9.8 m/s。

三、悬链线长度计算的实际应用在实际工程中，悬链线长度计算有着广泛的应用。

例如，在设计桥梁时，需要考虑桥梁的跨度、桥面宽度、桥墩高度等因素，这些因素都会影响到悬链线的长度。

因此，通过悬链线长度计算，可以优化桥梁的设计方案，提高桥梁的安全性和稳定性。

此外，在机械设计领域，悬链线长度计算也有着重要意义。

例如，在设计起重机吊臂时，需要根据吊臂的长度、高度和承重能力等因素，计算出合适的悬链线长度，以确保吊臂在承受最大负荷时仍能保持稳定。

四、悬链线长度计算的注意事项在进行悬链线长度计算时，需要注意以下几点：1.确保计算公式的准确性。

在计算悬链线长度时，要使用正确的计算公式，并确保公式中的各个参数准确无误。

2.考虑实际情况。

在实际工程中，悬链线的长度会受到多种因素的影响，因此在计算悬链线长度时，需要综合考虑这些因素，以确保计算结果的准确性。

3.采用适当的单位。

在计算悬链线长度时，需要使用适当的单位，例如米、厘米等。

这样可以确保计算结果的准确性和可读性。

悬链线科技名词定义中文名称：悬链线英文名称：catenary定义：两端悬挂的理想柔性软索的曲线。

工程计算中，可近似用抛物线计算。

应用学科：电力（一级学科）；输电线路（二级学科）以上内容由全国科学技术名词审定委员会审定公布目录悬链线等高悬链线数学表达式的证明工程中的应用悬链线悬链线(Catenary) 是一种曲线，它的形状因与悬在两端的绳子因均匀引力作用下掉下来之形相似而名。

适当选择坐标系后，悬链线的方程是一个双曲余弦函数，其公式为：y = a*cosh(x/a) 其中a 是一个常数。

等高悬链线数学表达式的证明注释如右图，设最低点A处受水平向左的拉力H，右悬挂点处表示为C点，在AC弧线区段任意取一段设为B点，则B受一个斜向上的拉力T，设T 和水平方向夹角为θ，绳子的质量为m,受力分析有：Tsinθ=mg；Tcosθ=H，tanθ=dy/dx=mg/H，mg=ρs，，其中s是右段AB 绳子的长度，ρ是绳子线重量密度，代入得微分方程dy/dx=ρs/H;利用弧长公式ds=√(1+dy^2/dx^2)*dx;所以s=∫√(1+dy^2/dx^2)*dx; 所以把s 带入微分方程得dy/dx=ρ∫√(1+dy^2/dx^2)*dx/H;.....(1) 对于(1)设p=dy/dx微分处理得p'=ρ/H*√(1+p^2)......(2) p'=dp/dx; 对（2）分离常量求积分∫dp/√(1+p^2)=∫ρ/H*dx 得ln[p+√(1+p^2)]=ρx/H+C，即asinhp（反双曲正弦）=ρx/H+C 当x=0时，dy/dx=p=0；带入得C=0；整理得asinhp=ρx/H 另祥解：（ln[p+√(1+p^2)]=ρx/H）；p=sh(ρx/H) （1+p^2=e^(2ρx/H)-2pe^(ρx/H)+p^2）；(p=[e^(ρx/H)-e^(-ρx/H)]/2=dy/dx)；y=ch (ρx/H)* H / ρ（y=H/(2ρ)*[e^(ρx/H)+e^(-ρx/H)] ）；令a=H/ρ：y=a*cosh (x/a) (y=a[e^(x/a)+e^(-x/a)]/(2)= a*cosh(x/a))。

导线悬链线解析方程式因为计算过程会出现双曲函数，所以先简单了解一下双曲函数在数学中，双曲函数是一类与常见的三角函数（也叫圆函数）类似的函数。

最基本的双曲函数是双曲正弦函数sinh 和双曲余弦函数cosh ，从它们可以导出双曲正切函数tanh 等，其推导也类似于三角函数的推导。

双曲函数的反函数称为反双曲函数，有反双曲正弦函数 arcsinh ，反双曲余弦函数arccosh ，反双曲正切函数 arctanh 。

双曲函数的定义和三角函数有如下关系sinhx=-isinixcoshx=cosixtanhx=\frac{sinhx}{coshx}=\frac{-isinix}{cosix}=-itanixi 是虚数单位sinhx 和 tanhx 都是奇函数， sinh(-x)=-sinhx ， tanh(-x)=-tanhxcoshx 是偶函数， cosh(-x)=coshx双曲正弦和双曲余弦导数关系:(求导方式就是把虚数单位 i 当成常数，其它步骤一样)(sinhx)'=coshx(coshx)'=sinhx双曲函数还可以用指数函数来表示根据欧拉公式 e^{ix}=cosx+isinx得 e^{x}=e^{i(-ix)}=cosix-isinix=coshx+sinhxe^{-x}=e^{i(ix)}=cosix+isinix=coshx-sinhx即 sinhx=\frac{e^{x}-e^{-x}}{2} ，coshx=\frac{e^{x}+e^{-x}}{2}接下来看悬链线悬链线是一根密度均匀的绳子或铁链两端固定在水平杆上，受重力的作用自然下垂后形成的曲线既然能保持平衡，那这根绳子上一定处处都满足二力平衡。

绳子受到重力以及自身张力假设一条不可伸长的线密度为 \rho 的绳子处于重力加速度为g 的重力场中，取绳子上某一小段受力分析，这小段在 x 轴上的投影是 dx小段绳子和水平面夹角的正切值就是悬链线方程在那一点的导数 y'可以证明，这段绳子的长度为dl=\frac{dx}{cos\theta}=\sqrt{1+tan^{2}\theta}dx=\sqrt {1+y'^{2}}dx图为受力分析所受重力为 mg=\rho dl=\rho g\sqrt{1+y'^{2}}dx ，受到的它前面那段绳子的拉力为T(x+dx)=(T_{x}(x+dx),T_{y}(x+dx)) ，且T_{y}=T_{x}y' ，它对后面那段绳子的拉力为T(x)=(T_{x}(x),T_{y}(x)) 。

悬链线长度计算（实用版）目录1.引言2.悬链线的定义和性质3.悬链线长度计算的公式推导4.悬链线长度计算的实际应用5.总结正文1.引言悬链线，又称为悬链曲线，是一种常见的数学曲线，其形状由一条水平直线和一条垂直直线构成，形状类似于一个倒挂着的链条。

悬链线在数学中有着广泛的应用，其中一个重要的应用就是计算其长度。

本文将介绍悬链线的定义和性质，并详细推导悬链线长度计算的公式，最后将讨论悬链线长度计算在实际应用中的价值。

2.悬链线的定义和性质悬链线可以定义为垂直于一个固定轴的直线上的一个点，以固定轴为圆心，作等速圆周运动，其轨迹形成的曲线。

悬链线具有以下性质：（1）悬链线关于垂直于轴线的平面对称。

（2）悬链线上任意一点的切线与轴线垂直。

（3）悬链线的长度等于圆周运动的半径与圆周运动所对应的圆心角的弧长。

3.悬链线长度计算的公式推导为了计算悬链线的长度，我们需要先推导出悬链线长度计算的公式。

假设悬链线长度为 L，圆周运动的半径为 r，圆心角为θ，则根据圆的性质，有：θ = 2πr / L解得：L = 2πr / θ这就是悬链线长度计算的公式。

4.悬链线长度计算的实际应用悬链线长度计算在实际中有很多应用，例如在建筑结构分析中，可以用悬链线长度计算来分析悬链式桥梁的稳定性；在机械工程中，可以用悬链线长度计算来设计摆线针轮等传动装置。

通过悬链线长度计算，可以更好地理解和优化这些实际问题。

5.总结悬链线是一种重要的数学曲线，其在实际中有着广泛的应用。

通过推导悬链线长度计算的公式，我们可以更好地理解和优化实际问题。

通常任何材料包括导线在内,都具有一定得刚性,但由于悬挂在杆塔上得一档导线相对较长,因此导线材料得刚性对其几何形状得影响很小,故在计算中假定:ﻫ(１)导线为理想得柔索。

因此,导线只承受轴向张力(或拉力),任意一点得弯矩为ﻫ零。

这样导线力学计算可应用理论力学中得柔索理论进行计算。

ﻫ(2)作用在导线上得荷载均指同一方向,且沿导线均匀分布。

一、悬链线方程及曲线弧长1。

悬链线方程为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差得情况讨论导线得应力及几何关系。

实际上,导线悬在空中得曲线形态,从数学角度用什么方程来描述就是进行导线力学分析得前题、由于假定视导线为柔索,则可按照理论力学中得悬链线关系来进行分析,即将导线架设在空中得几何形态视为悬链形态,而由此导出得方程式为悬链线方程。

如图2－5所示,给出了悬挂于A、B两点间得一档导线,假定为悬挂点等高得孤立档,设以导线得最低点Ｏ点为原点建立直角坐标系。

ﻫ图２—5导线悬链线及坐标系同时假定导线固定在导线所在得平面,可随导线一起摆动,显然这就是一个平面力系。

根据这个坐标进行导线得受力分析,可建立导线得悬链线方程、ﻫ我们先从局部受力分析开始,再找出其一般规律、首先在导线上任取一点D(x,y),然后分析ＯD段导线得受力关系,由图2—5所示,此OD段导线受三个力而保持平衡,其中D点承受拉力为T x=σｘS,它与导线曲线相切,与x轴夹角为α; O点承受拉力为Ｔ０=σ0Ｓ,T0为导线O点得切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身得荷载为G＝gSL x, 其中L x为OＤ段导线得弧长。

ﻫ将OD段导线得受力关系画为一个三角形表示,如图2－6所示,ﻫﻫ图2-６导线受力情况ﻫ由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力得代数与分别等于零。

或沿x 轴或y轴上分力代数与分别等于零。

垂直方向分力G＝T x siｎα=gSLｘ;水平方向分为Ｔ0=T xｃosα=σ0Ｓ、其中σ0、T0为导线最低点得应力与张力,σx、T x为导线任一点得应力与张力,S、g为导线截面与比载。

第二章导线应力弧垂分析第三节悬点等高时导线弧垂、线长和应力关系一、悬链线方程及曲线弧长1.悬链线方程为了分析方便，我们先从悬挂点等高，即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。

实际上，导线悬在空中的曲线形态，从数学角度用什么方程来描述是进行导线力学分析的前题。

由于假定视导线为柔索，则可按照理论力学中的悬链线关系来进行分析，即将导线架设在空中的几何形态视为悬链形态，而由此导出的方程式为悬链线方程。

如图2－5所示，给出了悬挂于A、B两点间的一档导线，假定为悬挂点等高的孤立档，设以导线的最低点O点为原点建立直角坐标系。

图2-5导线悬链线及坐标系同时假定导线固定在导线所在的平面，可随导线一起摆动，显然这是一个平面力系。

根据这个坐标进行导线的受力分析，可建立导线的悬链线方程。

我们先从局部受力分析开始，再找出其一般规律。

首先在导线上任取一点D（x,y），然后分析OD段导线的受力关系，由图2－5所示，此OD段导线受三个力而保持平衡，其中D 点承受拉力为T x=σx S，它与导线曲线相切，与x轴夹角为α；O点承受拉力为T0=σ0S，T0为导线O点的切线方向，恰与x轴平行，故又称水平张力；此外还有OD段导线自身的荷载为G=gSL x，其中L x为OD段导线的弧长。

将OD段导线的受力关系画为一个三角形表示，如图2－6所示，图2-6导线受力情况由静力学平衡条件可知，在平面坐标系中，其水平分力，垂直分力的代数和分别等于零。

或沿x轴或y轴上分力代数和分别等于零。

垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S。

其中σ0、T0为导线最低点的应力和张力，σx、T x为导线任一点的应力和张力，S、g为导线截面和比载。

将上述二式相比，则可求得导线任意一点D的斜率为：(2-10)由微分学知识可知，曲线上任一点的导数即为切线的斜率。

式（2－10）是悬链曲线的微分方程。

我们要用坐标关系表示出导线受力的一般规律，还需要将不定量L x消去，因此，将式对x微分得：（微分学中弧长微分公式为dS2=(dx)2+(dy)2）将上式移项整理后，两端进行积分这是个隐函数，因此，再进行分离变量积分，查积分公式有：（2－11）再进行分离变量积分，有于是，导线任一点D的纵坐标为：（2－12）式（2－12）是悬链方程的普通形式，其中C1和C2为积分常数，其值可根据取坐标原点的位置及初始条件而定。