中科大Fluent讲稿(完整版,完美整理).

第三章，湍流模型第一节， 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。

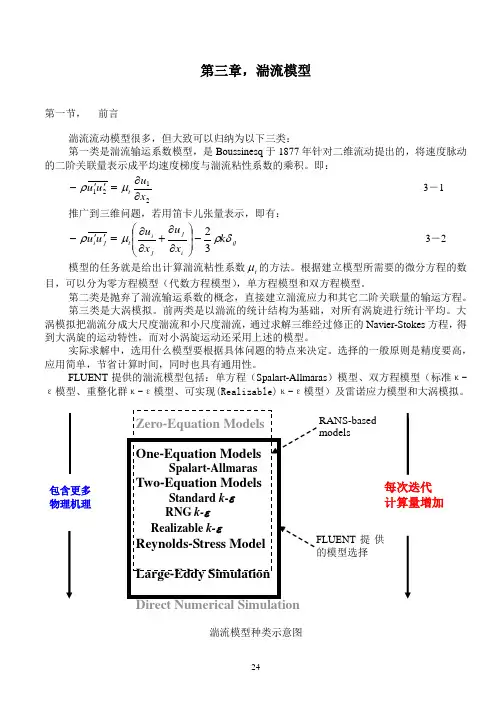
即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量表示，即有：ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 模型的任务就是给出计算湍流粘性系数t μ的方法。

根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。

第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。

第三类是大涡模拟。

前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。

大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。

实际求解中，选用什么模型要根据具体问题的特点来决定。

选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。

FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。

湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提供RANS-based models第二节，平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。

对于速度，有：i i i u u u '+= 3－3其中，i u 和i u '分别是平均速度和脉动速度（i=1,2,3）类似地，对于压力等其它标量，我们也有：φφφ'+= 3－4 其中，φ表示标量，如压力、能量、组分浓度等。

中科大FLUENT讲稿离散相模拟离散相模拟FLUENT 程序除了模拟连续相以外，也可以在Lagrangian 坐标系下模拟离散相。

离散相为球形颗粒（也可以是水滴或气泡）弥散在连续相中。

FLUENT 可以计算离散相的颗粒轨道，以及其与连续相之间的质量和能量交换。

耦合求解连续相和离散相，可以考虑相间的相互作用及影响。

离散相处理过程中，可以考虑以下因素：1，在Lagrangian 坐标系下，计算离散相在定常和非定常流动中的颗粒轨道。

2，连续相涡旋产生的湍流对离散相的影响3，离散相的加热与冷却过程4，液滴的蒸发与沸腾5，颗粒燃烧，包括挥发分挥发和碳核燃烧，用以模拟粉煤燃烧过程。

Fluent 假设离散相足够稀疏，忽略颗粒与颗粒之间的相互作用，也不考虑颗粒体积分数对连续相的影响。

因此在用该方法模拟实际过程时，要保证离散相的体积分数应该小于10％～12％。

离散相模型对以下流动过程不适合。

1，流向周期性流动2，如果采用预混燃烧模型，就不能考虑颗粒的化学反应。

3，采用多坐标系的流动采用颗粒轨道模型计算离散相时，需要给出颗粒的初始位置，速度，颗粒大小，温度及颗粒的物性参数。

颗粒轨道的计算根据颗粒的力平衡计算。

颗粒的传热传质则根据颗粒与连续相间的对流和辐射换热及质量交换来计算。

颗粒轨道，颗粒传热传质计算结果可以用图的形式给出。

颗粒轨道计算根据作用在颗粒（液滴，气泡）上力平衡，可以给出颗粒在Lagrangian 坐标系下的运动方程：x p p x p D pF g u u F dt du +-+-=ρρρ/)()( （8－1）其中，24Re 182D pp D C D F ρμ=，u 是连续相速度，p u 是颗粒速度，μ是流体的分子粘性系数，p ρρ,分别是流体与颗粒的密度；p D 是颗粒直径，Re 是相对雷诺数，定义为：μρuu D p p -=Re 阻力系数2321Re Re ααα++=D C ，1α，2α，3α为常数，根据光滑球颗粒实验结果给出[L114]。

2023年Fluent教程讲解一、概述在当今社会，计算机软件的应用已经渗透到生活的方方面面，流体力学仿真软件FLUENT作为目前流体力学领域最为流行的软件之一，在工程领域具有广泛的应用。

对于初学者来说，学习使用FLUENT进行流体力学仿真有一定的难度，因此有必要推出一份详细的FLUENT教程，以方便广大用户更快速、更有效地掌握使用该软件的技巧。

二、FLUENT教程概述1. 课程背景：本教程旨在针对初学者和需要系统复习的用户，全面深入地讲解FLUENT软件的使用方法和流体力学仿真原理。

2. 教程目标：通过本教程的学习，学员将能够掌握FLUENT软件的基本操作技能、流体力学仿真的基本原理和方法，以及解决实际工程问题的能力。

3. 教程内容：本教程将涵盖FLUENT软件的基本界面介绍、网格划分、边界条件设置、求解器选择、结果分析等方面内容，同时还将讲解一些典型的流体力学仿真案例。

三、教程具体内容1. FLUENT软件的安装和配置 - 硬件要求- 软件安装步骤- 许可授权获取2. FLUENT软件的基本操作- 软件界面介绍- 各个功能区的作用- 鼠标操作技巧3. 流体力学仿真的基本原理- 流体动力学基础知识回顾 - 数值模拟方法简介- 边界条件和初始条件的设置4. 网格的划分和优化- 网格划分的基本步骤- 网格质量的评估和优化方法 - 网格划分实例讲解5. 边界条件和求解器的选择- 不同边界条件的设置方法- 不同求解器的选择和对比- 求解器参数调节技巧6. 结果的后处理和分析- 数据的导出和保存- 结果的可视化处理- 结果分析及工程应用7. 典型流体力学仿真案例- 工程流动问题- 空气动力学问题- 液体传热问题四、教程特色- 本教程以实例驱动学习，将通过丰富的仿真案例来讲解FLUENT软件的实际操作技巧和流体力学仿真的基本原理，帮助学员更好地理解和掌握知识。

- 本教程通过图文结合的方式展示软件操作步骤，力求使学员能够更直观地理解FLUENT软件的使用方法。

一、基本设置1．Double Precision的选择启动设置如图，这里着重说说Double Precision（双精度）复选框，对于大多数情况，单精度求解器已能很好的满足精度要求，且计算量小，这里我们选择单精度。

然而对于以下一些特定的问题，使用双精度求解器可能更有利[1]。

a.几何特征包含某些极端的尺度（如非常长且窄的管道），单精度求解器可能不能足够精确地表达各尺度方向的节点信息。

b.如果几何模型包含多个通过小直径管道相互连接的体，而某一个区域的压力特别大（因为用户只能设定一个总体的参考压力位置），此时，双精度求解器可能更能体现压差带来的流动（如渐缩渐扩管的无粘与可压缩流动模拟）。

c.对于某些高导热系数比或高宽纵比的网格，使用单精度求解器可能会遇到收敛性不佳或精确度不足不足的问题，此时，使用双精度求解器可能会有所帮助。

[1] 李鹏飞,徐敏义,王飞飞.精通CFD工程仿真与案例实战：FLUENT GAMBIT ICEM CFD Tecplot[M]. 北京,人民邮电出版社,2011:114-1162．网格光顺化用光滑和交换的方式改善网格：通过Mesh下的Smooth/Swap来实现，可用来提高网格质量，一般用于三角形或四边形网格，不过质量提高的效果一般般，影响较小，网格质量的提高主要还是在网格生成软件里面实现，所以这里不再用光滑和交换的方式改善网格，其原理可参考《FLUENT全攻略》（已下载）。

3．Pressure-based与Density-based求解器设置如图。

下面说一说Pressure-based和Density-based 的区别：Pressure-Based Solver是Fluent的优势，它是基于压力法的求解器，使用的是压力修正算法，求解的控制方程是标量形式的，擅长求解不可压缩流动，对于可压流动也可以求解；Fluent 6.3以前的版本求解器，只有Segregated Solver和Coupled Solver，其实也是Pressure-Based Solver的两种处理方法；Density-Based Solver是Fluent 6.3新发展出来的，它是基于密度法的求解器，求解的控制方程是矢量形式的，主要离散格式有Roe，AUSM+，该方法的初衷是让Fluent具有比较好的求解可压缩流动能力，但目前格式没有添加任何限制器，因此还不太完善；它只有Coupled的算法；对于低速问题，他们是使用Preconditioning方法来处理，使之也能够计算低速问题。

想起CFD，人们总会想起FLUENT，丰富的物理模型使其应用广泛，从机翼空气流动到熔炉燃烧，从鼓泡塔到玻璃制造，从血液流动到半导体生产，从洁净室到污水处理工厂的设计，另外软件强大的模拟能力还扩展了在旋转机械，气动噪声，内燃机和多相流系统等领域的应用。

今天，全球数以千计的公司得益于FLUENT的这一工程设计与分析软件，它在多物理场方面的模拟能力使其应用范围非常广泛，是目前功能最全的CFD软件。

FLUENT因其用户界面友好，算法健壮，新用户容易上手等优点一直在用户中有着良好的口碑。

长期以来，功能强大的模块，易用性和专业的技术支持所有这些因素使得FLUENT成为企业选择CF D软件时的首选。

网格技术，数值技术，并行计算计算网格是任何CFD计算的核心，它通常把计算域划分为几千甚至几百万个单元，在单元上计算并存储求解变量，FLUENT使用非结构化网格技术，这就意味着可以有各种各样的网格单元：二维的四边形和三角形单元，三维的四面体核心单元、六面体核心单元、棱柱和多面体单元。

这些网格可以使用FLUENT的前处理软件GAMBIT自动生成，也可以选择在ICEM CFD工具中生成。

六面体核心网格四边形平铺网格在目前的CFD市场， FLUENT以其在非结构网格的基础上提供丰富物理模型而著称，久经考验的数值算法和鲁棒性极好的求解器保证了计算结果的精度，新的NITA算法大大减少了求解瞬态问题的所需时间，成熟的并行计算能力适用于NT，Linux或Unix平台，而且既适用单机的多处理器又适用网络联接的多台机器。

动态加载平衡功能自动监测并分析并行性能，通过调整各处理器间的网格分配平衡各CPU的计算负载。

并行速度的比较湍流和噪声模型FLUENT的湍流模型一直处于商业CFD软件的前沿，它提供的丰富的湍流模型中有经常使用到的湍流模型、针对强旋流和各相异性流的雷诺应力模型等，随着计算机能力的显著提高，FLUENT已经将大涡模拟（LES）纳入其标准模块，并且开发了更加高效的分离涡模型（DES），FLUENT提供的壁面函数和加强壁面处理的方法可以很好地处理壁面附近的流动问题。

第四章DEFINE宏本章介绍了Fluent公司所提供的预定义宏，我们需要用这些预定义宏来定义UDF。

在这里这些宏就是指DEFINE宏。

本章由如下几节组成：∙ 4.1 概述∙ 4.2 通用解算器DEFINE宏∙ 4.3 模型指定DEFINE宏∙ 4.4 多相DEFINE宏∙ 4.5 离散相模型DEFINE宏4.1 概述DEFINE宏一般分为如下四类：∙通用解算器∙模型指定∙多相∙离散相模型(DPM)对于本章所列出的每一个DEFINE宏，本章都提供了使用该宏的源代码的例子。

很多例子广泛的使用了其它章节讨论的宏，如解算器读取（第五章）和utilities (Chapter 6)。

需要注意的是，并不是本章所有的例子都是可以在FLUENT中执行的完整的函数。

这些例子只是演示一下如何使用宏。

除了离散相模型DEFINE宏之外的所有宏的定义都包含在udf.h文件中。

离散相模型DEFINE宏的定义包含在dpm.h文件中。

为了方便大家，所有的定义都列于附录A中。

其实udf.h头文件已经包含了dpm.h文件，所以在你的UDF源代码中就不必包含dpm.h文件了。

注意：在你的源代码中，DEFINE宏的所有参变量必须在同一行，如果将DEFINE声明分为几行就会导致编译错误。

4.2 通用解算器DEFINE宏本节所介绍的DEFINE宏执行了FLUENT中模型相关的通用解算器函数。

表4.2.1提供了FLUENT中DEFINE宏，以及这些宏定义的功能和激活这些宏的面板的快速参考向导。

每一个DEFINE宏的定义都在udf.h头文件中，具体可以参考附录A。

∙DEFINE_ADJUST (4.2.1节)∙DEFINE_INIT (4.2.2节)∙DEFINE_ON_DEMAND (4.2.3节)∙DEFINE_RW_FILE (4.2.4节)表4.2.1：通用解算器DEFINE宏的快速参考向导功能DEFINE宏激活该宏的面板处理变量DEFINE_ADJUST User-Defined Function Hooks初始化变量DEFINE_INIT User-Defined Function Hooks异步执行DEFINE_ON_DEMAND Execute On Demand读写变量到……DEFINE_RW_FILE User-Defined Function Hooks Case和data文件∙ 4.2.1 DEFINE_ADJUST∙ 4.2.2 DEFINE_INIT∙ 4.2.3 DEFINE_ON_DEMAND∙ 4.2.4 DEFINE_RW_FILE4.2.1 DEFINE_ADJUST功能和使用方法的介绍DEFINE_ADJUST是一个用于调节和修改FLUENT变量的通用宏。

第四章，湍流流动的近壁处理壁面对湍流有明显影响。

在很靠近壁面的地方,粘性阻尼减少了切向速度脉动,壁面也阻止了法向的速度脉动。

离开壁面稍微远点的地方，由于平均速度梯度的增加,湍动能产生迅速变大，因而湍流增强。

因此近壁的处理明显影响数值模拟的结果,因为壁面是涡量和湍流的主要来源。

实验研究表明，近壁区域可以分为三层,最近壁面的地方被称为粘性底层，流动是层流状态，分子粘性对于动量、热量和质量输运起到决定作用。

外区域成为完全湍流层，湍流起决定作用。

在完全湍流与层流底层之间底区域为混合区域(Blending region），该区域内分子粘性与湍流都起着相当的作用.近壁区域划分见图4－1。

图4－1，边界层结构第一节，壁面函数与近壁模型近壁处理方法有两类：第一类是不求解层流底层和混合区,采用半经验公式(壁面函数）来求解层流底层与完全湍流之间的区域.采用壁面函数的方法可以避免改进模型就可以直接模拟壁面存在对湍流的影响.第二类是改进湍流模型，粘性影响的近壁区域，包括层流底层都可以求解.对于多数高雷诺数流动问题,采用壁面函数的方法可以节约计算资源.这是因为在近壁区域，求解的变量变化梯度较大，改进模型的方法计算量比较大。

由于可以减少计算量并具有一定的精度,壁面函数得到了比较多的应用.对于许多的工程实际流动问题,采用壁面函数处理近壁区域是很好的选择。

如果我们研究的问题是低雷诺数的流动问题，那么采用壁面函数方法处理近壁区域就不合适了，而且壁面函数处理的前提假设条件也不满足。

这就需要一个合适的模型，可以一直求解到壁面.FLUENT提供了壁面函数和近壁模型两种方法,以便供用户根据自己的计算问题选择。

4。

1。

1壁面函数FLUENT提供的壁面函数包括：1,标准壁面函数;2，非平衡壁面函数两类。

标准壁面函数是采用Launder and Spalding [L93］的近壁处理方法。

该方法在很多工程实际流动中有较好的模拟效果。

4。

1。

1.1 标准壁面函数根据平均速度壁面法则,有：**1ln()U Ey k=4－1 其中，1/41/2*/p pw U C k U μτρ≡,1/41/2*p p C k y y μρμ≡，并且k ＝0。

第四章DEFINE宏本章介绍了Fluent公司所提供的预定义宏，我们需要用这些预定义宏来定义UDF。

在这里这些宏就是指DEFINE宏。

本章由如下几节组成：• 4.1 概述• 4.2 通用解算器DEFINE宏• 4.3 模型指定DEFINE宏• 4.4 多相DEFINE宏• 4.5 离散相模型DEFINE宏4.1 概述DEFINE宏一般分为如下四类：•通用解算器•模型指定•多相•离散相模型(DPM)对于本章所列出的每一个DEFINE宏，本章都提供了使用该宏的源代码的例子。

很多例子广泛的使用了其它章节讨论的宏，如解算器读取（第五章）和utilities (Chapter 6)。

需要注意的是，并不是本章所有的例子都是可以在FLUENT中执行的完整的函数。

这些例子只是演示一下如何使用宏。

除了离散相模型DEFINE宏之外的所有宏的定义都包含在udf.h文件中。

离散相模型DEFINE宏的定义包含在dpm.h文件中。

为了方便大家，所有的定义都列于附录A中。

其实udf.h头文件已经包含了dpm.h文件，所以在你的UDF源代码中就不必包含dpm.h文件了。

注意：在你的源代码中，DEFINE宏的所有参变量必须在同一行，如果将DEFINE声明分为几行就会导致编译错误。

4.2 通用解算器DEFINE宏本节所介绍的DEFINE宏执行了FLUENT中模型相关的通用解算器函数。

表4.2.1提供了FLUENT中DEFINE宏，以及这些宏定义的功能和激活这些宏的面板的快速参考向导。

每一个DEFINE宏的定义都在udf.h头文件中，具体可以参考附录A。

•DEFINE_ADJUST (4.2.1节)•DEFINE_INIT (4.2.2节)•DEFINE_ON_DEMAND (4.2.3节)•DEFINE_RW_FILE (4.2.4节)• 4.2.1 DEFINE_ADJUST• 4.2.2 DEFINE_INIT• 4.2.3 DEFINE_ON_DEMAND• 4.2.4 DEFINE_RW_FILE4.2.1 DEFINE_ADJUST功能和使用方法的介绍DEFINE_ADJUST是一个用于调节和修改FLUENT变量的通用宏。

中科大FLUENT讲稿第七章自定义函数中科大fluent讲稿第七章自定义函数第七章自定义函数7.1，详述我们可以用udfs来定义：a)边界条件b)源项c)物性定义（除了比热外）d)表面和体积反应速率e)用户自定义标量截叶方程f)离散相模型（例如体积力，拉力，源项等）g)代数滑流（algebraicslip）混合物模型（滑流速度和微粒尺寸）h)变量初始化i)壁面热流量j)使用用户自定义标量后处理边界条件udfs能产生依赖时间，加速度和流场变量有关的边界条件。

比如，我们可以定义依赖流动时间的x方向的速度入口，或定义依赖边线的温度边界。

边界条件剖面udfs用宏define_profile定义。

有关例子可以在5.1和6.1中找出。

源项udfs可以定义除了do电磁辐射模型之外的任一截叶方程的源项。

它用宏define_source定义。

有关例子在5.2和6.2中可以找出。

物性udfs需用去定义物质的物理性质，除了比热容之外，其它物性参数都可以定义。

比如，我们可以定义依赖温度的粘性系数。

它用宏define_property定义，有关例子在6.3中。

反应速率udfs用以定义表面或体积反应的反应速率，分别用宏define_sr_rate和define_vr_rate定义，例子见到6.4。

线性二者模型用宏define_dpm定义有关参数，见到5.4。

udfs还可以对任一用户自定义标量的截叶方程展开初始化，定义壁面热流量，或排序暂存变量值（用用户自定义标量或用户自定义内存量）并使之用作后处理。

有关的应用领域载于5.3，5.5，5.6和5.7。

7.1.1书写udfs的基本步骤在采用udfs处置fluent模型的过程中，我们通常按照下面五步展开：1．概念上函数设计2．采用c语言书写3．编程调试c程序4．继续执行udf5．分析与比较结果第一步分析我们所处置的模型，目的就是获得我们必须书写的udf的数学表达式。

第二步将数学表达式转化成c语言源代码。