§1二重积分概念

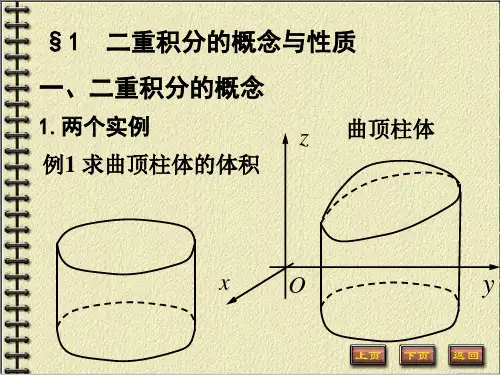
第二十一章 二重积分§1 二重积分概念教学目的与要求：1.掌握二重积分的定义和性质, 二重积分的可积条件.2.了解有界闭区域上的连续函数的可积性.3.了解平面点集可求面积的充要条件.教学重点：二重积分的定义和性质.教学难点：二元函数可积条件.教学过程一、平面图形的面积（一）、内、外面积（约当，黎曼外内测度）的概念直线网T 分割平面图形P ，T 的网眼中小闭矩形i ∆的分类：（ⅰ）i ∆含的全是P 的内点,（ⅱ）i ∆含的全是P 的外点（不含P 的点）,（ⅲ）i ∆内含有P 的边界点,记()T s P 为T 的第ⅰ类i ∆的面积的和．记()T S P 为T 的第ⅰ和第三类i ∆的面积的和．记P I =(){}T s P T sup ，称为P 的内面积． 记P I =(){}T S P T inf ，称为P 的外面积．定义1 若平面图形P 的内面积P I 等于它的外面积P I ，则称P 为可求面积，并称其共同值P I =P I =P I 为P 的面积（约当，黎曼测度）定理21.1 平面有界图形P 可求面积的充要条件是：对任给的0>ε，总存在直线网T ，使得()()ε<-T s T S P P . （2）证明 [必要性]设平面有界图形P 的面积为P I ．由定义1，有P I =P I =P I ．对任给的ε，由P I 及P I 的定义知道，分别存在直线网1T 与2T ，使得记T 为由1T 与2T 这两个直线网合并的直线网，可证得()()T s T s P P ≤1，()()T S T S P P ≥2， (3)于是由（3）可得从而得到对直线网T 有 ()()ε<-T s T S P P ，[充分性]对任给的0>ε，存在直线网T ，使得（2）式成立．但所以 ()()ε<-≤-T s T S I I P P P P ，由ε的任意性，因此P I =P I ，因而平面图形P 可求面积．推论 平面有界图形P 的面积为零的充要条件是它的外面积0=P I ，即对任给的0>ε，存在直线网T ，使得，或对任给的0>ε，平面图形P 能被有限个其面积总和小于ε的小矩形所覆盖． 定理21.2 平面有界图形P 可求面积的充要条件是：P 的边界K 的面积为零．证明 由定理21．1，P 可求面积的充要条件是：对任给的0>ε，存在直线网T ，使得()()ε<-T s T S P P ．由于所以也有()ε<T S K ．由上述推论，P 的边界K 的面积为零．定理21.3 若曲线K 为由定义在[]b a ,上的连续函数()x f 的图象，则曲线K 的面积为零证明 由于()x f 在闭区间[]b a ,上连续函数，从而一致连续．因而对任给的0>ε，总存在0>δ，当把区间[]b a ,分成n 个小区间[]i i x x ,1-()n i ,,1 =并且满足{}n i x x x i i i ,,1max 1 =-=∆-δ<时，可使在每个小区间[]i i x x ,1-上的振幅都成立a b i -<εω．现把曲线K 按自变量n x x x x ,,,10 =分成n 个小段，这时每一个小段都能被以i x ∆为宽，i ω为高的小矩形甩覆盖．由于这个小矩形面积的总和为 所以由定理21．1的推论即得曲线K 的面积为零．还可证明得到：由参量方程()()()βαψϕ≤≤==t t Y t x ,所表示的光滑曲线或按段光滑曲线，其面积为零．二、 二重积分的定义及其存在性背景：求某曲顶柱体的体积时，通过“分割、近似，求和、取极限”的步骤，利用求柱体的体积的方法来得到结果．一类大量的“非均匀”问题都采用类似的方法，从而归结出下面一类积分的定义．定义 设()y x f ,是定义在可求面积的有界闭区域D 上的函数，用任意曲线把D 分成n 个可求面积的小区域：,,,,21n σσσ∆∆∆ 以i σ∆表示i σ∆的面积，这些小区域构成D 的一个分割T ，以i d 表示i σ的直径，称{}i n i d T ≤≤=1max 为分割T 的细度，在每一个i σ上任取一点（i i ηξ,），作和式： ∑=∆n i i i i f 1),(σηξ，称之为函数在上属于分割的一个积分和． 定义2 设()y x f ,是定义在可求面积的有界闭区域D 上的函数，J 是一个确定的数，若对任给的正数ε，总存在某个正数δ，使对于D 的任何分割T ，当它的细度δ<T 时，属于T 的所有积分和都有则称()y x f ,在D 上可积，数J 称为函数()y x f ,在D 上的二重积分，记作其中()y x f ,称为二重积分的被积函数，y x ,称为积分变量，D 称为积分区域．几何意义：当()y x f ,0≥时，二重积分()⎰⎰D d y x f σ,在几何上表示以=z ()y x f ,为曲顶，D 为底的曲顶柱体的体积.在直角坐标系下用平行于坐标轴的直线网来划分区域D ，则面积元素为dxdy d =σ直角坐标系下可表示为： ()⎰⎰D d y x f σ,=()⎰⎰D dxdy y x f ,.可积的必要条件：()y x f ,在可求面积的区域D 上有界函数()y x f ,在可求面积的区域D 上有界时，T 是D 的一个分割，把D 分成个可求面积的小区域n σσ,,1 ，令()y x f , 关于分割T 的上和与下和：定理21.4 ()y x f ,在D 上可积的充要条件是：定理21.5 ()y x f ,在D 上可积的充要条件是：对于任给的正数ε，存在D 的某个分割T ，使得()()ε<-T s T S ．定理21.6 有界闭区域D 上的连续函数必可积．定理21.7 设()y x f ,是定义在有界闭区域D 上的有界函数．若()y x f ,的不连续点都落在有限条光滑曲线上，则()y x f ,在D 上可积.证明 不失一般性，可设()y x f ,的不连续点全部落在某一条光滑曲线L上．记L 的长度为l ，于是对任给的ε>0，把L 等分成1+⎥⎦⎤⎢⎣⎡=εl n 段： 在每段i L 上取—点i P ，使段与其一端点的弧长为n l2，以i P 为中心作边长为ε的正方形i ∆，则i L ⊂i ∆，从而有n i i L 1=∆⊂记 n i i 1=∆⊂∆，则∆为一多边形．设∆的面积为W ，那么 现在把区域D 分成两部分．第一部分∆= D D 1．第二部分121D D D -=．由于()y x f ,在2D 上连续，根据定理21.6与定理21.5，存在2D 的分割2T ，使得()()ε<-22T s T S ．又记()()y x f M y x ,sup ,∆∈∆=，()()y x f m y x ,inf ,∆∈∆=，以T 表示由2T 与多边形∆的边界所组成的区域D 的分割，则有其中ω是()y x f ,在D 上的振幅．由于()y x f ,在D 上有界，故ω是有限值．于是由定理21，5就证明了()y x f ,在上可积.三、二重积分的性质二重积分具有一系列与定积分完全相类似的性质，现列举如下：1. 若()y x f ,在区域D 上可积，k 为常数，则k ()y x f ,在D 上也可积，且2．若()y x f ,,()y x g ,在D 上都可积，则()y x f ,±()y x g ,在D 上也可积，且()()[]⎰⎰±D d y x g y x f σ,,=()⎰⎰D d y x f σ,±()⎰⎰D d y x g σ,.3. 若()y x f ,在1D 和2D 上都可积，且1D 与2D 无公共内点，则()y x f ,在1D 2D 也可积，且()⎰⎰21,D D d y x f σ=()⎰⎰1,D d y x f σ+()⎰⎰2,D d y x f σ.4．若()y x f ,与()y x g ,在D 上可积，且()y x f ,≤()y x g ,，()∈y x ,D ，则5．若()y x f ,在D 上可积，则函数()y x f ,在D 上也可积，且6. 若()y x f ,在D 上可积．且 m ≤()y x f ,≤M ， ()∈y x , D则这里D S 是积分区域D 的面积．7．(中值定理) 若()y x f ,在有界闭区域D 上连续，则存在()∈ηξ,D ，使得 这里D S 是积分区域D 的面积．中值定理的几何意义：以D 为底，()())0,(,,≥=y x f y x f z 为曲顶的曲顶柱体体积等于一个同底的平顶柱体的体积，这个平顶柱体的高等于在()y x f ,区域D 中某点()ηξ,的函数值()ηξ,f ．作业2，4，5.。

第十一章 重积分§1 二重积分的概念1.把重积分⎰⎰D xydxdy 作为积分和的极限,计算这个积分值,其中D=[][]1,01,0⨯,并用直线网x=n i ,y=nj (i,j=1,2,…,n-1)分割这个正方形为许多小正方形,每一小正方形取其右上顶点为其界点.2.证明:若函数f 在矩形式域上D 可积,则f 在D 上有界.3.证明定理:若f 在矩形区域D 上连续,则f 在D 上可积.4.设D 为矩形区域,试证明二重积分性质2、4和7.性质2 若f 、g 都在D 上可积,则f+g 在D 上也可积,且()⎰+D g f =⎰⎰+D D g f . 性质4 若f 、g 在D 上可积,且g f ≤,则 ⎰⎰≤D Dg f , 性质7(中值定理) 若f 为闭域D 上连续函数,则存在()D ,∈ηξ,使得()D ,f f D∆ηξ=⎰. 5.设D 0、D 1和D 2均为矩形区域,且210D D D =,∅=11D int D int , 试证二重积分性质3.性质3(区域可加性) 若210D D D =且11D int D int ∅=,则f 在D 0上可积的充要条件是f 在D 1、D 2上都可积,且⎰0D f =⎰⎰+21D D f f , 6.设f 在可求面积的区域D 上连续,证明:(1)若在D 上()0y ,x f ≥,()0y ,x f ≠则0f D>⎰; (2)若在D 内任一子区域D D ⊂'上都有⎰'=D 0f ,则在D 上()0y ,x f ≡。

.7.证明:若f 在可求面积的有界闭域D 上连续,,g 在D 上可积且不变号,则存在一点()D ,∈ηξ,使得()()⎰⎰D dxdy y ,x g y ,x f =()ηξ,f ()⎰⎰Ddxdy y ,x g .8.应用中值定理估计积分⎰⎰≤-++10y x 22ycos x cos 100dxdy 的值§2 二重积分的计算1.计算下列二重积分:(1)()⎰⎰-Ddxdy x 2y ,其中D=[][]2,15,3⨯;(2)⎰⎰D2dxdy xy ,其中(ⅰ)D=[][]3,02,0⨯,(ⅱ)D=[]3,0 []2,0⨯; (3)()⎰⎰+Ddxdy y x cos ,其中D=[]π⨯⎥⎦⎤⎢⎣⎡π,02,0; (4)⎰⎰+D dx dy x y 1x ,其中D=[][]1,01,0⨯. 2. 设f(x,y)=()()y f x f 21⋅为定义在D=[]⨯11b ,a []22b ,a 上的函数,若1f 在[]11b ,a 上可积,2f 在[]22b ,a 上可积,则f 在D 上可积,且⎰D f =⎰⎰⋅1122b a b a 21f f . 3.设f 在区域D 上连续,试将二重积分()⎰⎰Ddxdy y ,x f 化为不同顺序的累次积分:(1)D 由不等式x y ≤,a y ≤,b x ≤()b a 0≤≤所确的区域:(2)D 由不等式222a y x ≤+与a y x ≤+(a>0)所确定的区域;(3)D=(){}1,≤+y x y x .4.在下列积分中改变累次积分的顺序:(1) ()⎰⎰20x 2x dy y ,x f dx ; (2) ()⎰⎰----11x 1x 122dy y ,x f dx ; (3)()⎰⎰10x 02dy y ,x f dy +()()⎰⎰-31x 3210dy y ,x f dx .5.计算下列二重积分:(1)⎰⎰D2dxdy xy ,其中D 由抛物线y=2px 与直线x=2p (p>0)所围的区域; (2)()⎰⎰+D 22dxdy y x,其中D=(){1x 0y ,x ≤≤, y x ≤ }x 2≤; (3)⎰⎰-D x a 2dx dy (a>0),其中D 为图(20—7)中的阴影部分； (4)⎰⎰Ddxdy x ,其中D=(){}x y x y ,x 22≤+; (5)⎰⎰D dxdy xy ,其中为圆域222a y x ≤+.6.写出积分()⎰⎰ddxdy y ,x f 在极坐标变换后不同顺序的累次积分:(1)D 由不等式1y x 22≤+,x y ≤,0y ≥所确定的区域;(2)D 由不等式2222b y x a ≤+≤所确定的区域;(3)D=(){}0x ,y y x y ,x 22≥≤+.7.用极坐标计算二重积分: (1) ⎰⎰+D22dxdy y x sin ,其中D=(){222y x y ,x +≤π }24π≤; (2)()⎰⎰+Ddxdy y x ,其中D=(){}y x y x y ,x 22+≤+; (3)()⎰⎰+'D22dxdy y x f ,其中D 为圆域222R y x ≤+.8.在下列符号分中引入新变量后,试将它化为累次积分:(1) ()⎰⎰--20x 2x 1dy y ,x f dx ,其中u=x+y,v=x-y;(2) ()dxdy y ,x f D⎰⎰,其中D=(){a y x y ,x ≤+,0x ≥, }0y ≥,若x=v cos U 4, v sin U y 4=.(3)()⎰⎰dxdy y ,x f ,其中D=(){a y x y ,x ≤+,0x ≥, }0y ≥,若x+y=u,y=uv.9.求由下列曲面所围立体V 的体积:(1) v 由坐标平面及x=2,y=3,x+y+Z=4所围的角柱体;(2) v 由z=22y x +和z=x+y 围的立体; (3) v 由曲面9y 4x Z 222+=和2Z=9y 4x 22+所围的立体.11.试作适当变换,计算下列积分:(1)()()⎰⎰-+Ddxdy y x sin y x ,D=(){π≤+≤y x 0y .x }π≤-≤y x 0;(2)⎰⎰+D y x y dxdy e,D=(){1y x y ,x ≤+,0x ≥,}0y ≥.12.设f:[a,b]→R 为连续函数,应用二重积分性质证明:()≤⎥⎦⎤⎢⎣⎡⎰2b a dx x f ()()⎰-b a 2dx x f a b ， 其中等号仅在f 为常量函数时成立。

二重积分的概念和计算方法在数学中，我们经常遇到需要对二维区域上的函数进行求和或求平均的情况。

为了解决这类问题，人们引入了二重积分的概念。

本文将探讨二重积分的概念以及常见的计算方法。

一、二重积分的概念二重积分是对二维平面上的函数进行求和的操作。

它可以看作是将一个二维区域分割成无穷多个小的矩形，然后对每个小矩形内的函数值进行求和的过程。

一般来说，我们通过累次积分的方法来计算二重积分。

对于函数f(x, y)在区域D上的二重积分，可以表示为：∬f(x, y)dA其中，D表示二维区域，dA表示微元面积。

二重积分的结果是一个数值，代表了函数f(x, y)在区域D上的总体特征。

二、二重积分的计算方法1. 直角坐标系下的二重积分在直角坐标系下，计算二重积分需要先确定积分范围。

一般情况下，我们将区域D分割成一个个小矩形或小三角形，根据积分的性质进行求和。

对于给定的函数f(x, y)，其在区域D上的二重积分可以表示为：∬f(x, y)dA = ∫∫f(x, y)dxdy其中，积分区域D的边界可以表示为[a, b]和[c(x), d(x)]，其中c(x)和d(x)是关于x的函数。

通过确定积分的次序和边界，我们可以将二重积分转化为一重积分的形式，然后按照一重积分的计算方法进行求解。

2. 极坐标系下的二重积分在某些情况下，使用极坐标系进行二重积分的计算更为方便。

特别是当积分区域具有简单的几何形状，如圆形、扇形或圆环等情况下，使用极坐标系可以简化计算过程。

对于给定的函数f(x, y)，在极坐标系下的二重积分可以表示为：∬f(x, y)dA = ∫∫f(r, θ)rdrdθ其中，积分区域D的边界可以表示为[r1(θ), r2(θ)]和[a, b]，其中r1(θ)和r2(θ)是关于θ的函数。

通过确定积分的次序和边界，我们可以将二重积分转化为一重积分的形式，然后按照一重积分的计算方法进行求解。

3. 格林公式的应用在某些情况下，利用格林公式可以简化二重积分的计算。

第十一章 重积分§1 二重积分的概念1.把重积分⎰⎰D xydxdy 作为积分和的极限,计算这个积分值,其中D=[][]1,01,0⨯,并用直线网x=n i ,y=nj (i,j=1,2,…,n-1)分割这个正方形为许多小正方形,每一小正方形取其右上顶点为其界点.2.证明:若函数f 在矩形式域上D 可积,则f 在D 上有界.3.证明定理(20.3):若f 在矩形区域D 上连续,则f 在D 上可积.4.设D 为矩形区域,试证明二重积分性质2、4和7.性质2 若f 、g 都在D 上可积,则f+g 在D 上也可积,且()⎰+D g f =⎰⎰+D D g f . 性质4 若f 、g 在D 上可积,且g f ≤,则 ⎰⎰≤D Dg f , 性质7(中值定理) 若f 为闭域D 上连续函数,则存在()D ,∈ηξ,使得()D ,f f D∆ηξ=⎰. 5.设D 0、D 1和D 2均为矩形区域,且210D D D =,∅=11D int D int , 试证二重积分性质3.性质3(区域可加性) 若210D D D =且11D int D int ∅=,则f 在D 0上可积的充要条件是f 在D 1、D 2上都可积,且⎰0D f =⎰⎰+21D D f f , 6.设f 在可求面积的区域D 上连续,证明:(1)若在D 上()0y ,x f ≥,()0y ,x f ≠则0f D>⎰; (2)若在D 内任一子区域D D ⊂'上都有⎰'=D 0f ,则在D 上()0y ,x f ≡。

.7.证明:若f 在可求面积的有界闭域D 上连续,,g 在D 上可积且不变号,则存在一点()D ,∈ηξ,使得()()⎰⎰D dxdy y ,x g y ,x f =()ηξ,f ()⎰⎰Ddxdy y ,x g .8.应用中值定理估计积分⎰⎰≤-++10y x 22ycos x cos 100dxdy 的值§2 二重积分的计算1.计算下列二重积分:(1)()⎰⎰-Ddxdy x 2y ,其中D=[][]2,15,3⨯;(2)⎰⎰D2dxdy xy ,其中(ⅰ)D=[][]3,02,0⨯,(ⅱ)D=[]3,0 []2,0⨯; (3)()⎰⎰+Ddxdy y x cos ,其中D=[]π⨯⎥⎦⎤⎢⎣⎡π,02,0; (4)⎰⎰+D dx dy x y 1x ,其中D=[][]1,01,0⨯. 2. 设f(x,y)=()()y f x f 21⋅为定义在D=[]⨯11b ,a []22b ,a 上的函数,若1f 在[]11b ,a 上可积,2f 在[]22b ,a 上可积,则f 在D 上可积,且⎰D f =⎰⎰⋅1122b a b a 21f f . 3.设f 在区域D 上连续,试将二重积分()⎰⎰Ddxdy y ,x f 化为不同顺序的累次积分:(1)D 由不等式x y ≤,a y ≤,b x ≤()b a 0≤≤所确的区域:(2)D 由不等式222a y x ≤+与a y x ≤+(a>0)所确定的区域;(3)D=(){}1,≤+y x y x .4.在下列积分中改变累次积分的顺序:(1) ()⎰⎰20x 2x dy y ,x f dx ; (2) ()⎰⎰----11x 1x 122dy y ,x f dx ; (3)()⎰⎰10x 02dy y ,x f dy +()()⎰⎰-31x 3210dy y ,x f dx .5.计算下列二重积分:(1)⎰⎰D2dxdy xy ,其中D 由抛物线y=2px 与直线x=2p (p>0)所围的区域; (2)()⎰⎰+D 22dxdy y x,其中D=(){1x 0y ,x ≤≤, y x ≤ }x 2≤; (3)⎰⎰-D x a 2dx dy (a>0),其中D 为图(20—7)中的阴影部分； (4)⎰⎰Ddxdy x ,其中D=(){}x y x y ,x 22≤+; (5)⎰⎰D dxdy xy ,其中为圆域222a y x ≤+.6.写出积分()⎰⎰ddxdy y ,x f 在极坐标变换后不同顺序的累次积分:(1)D 由不等式1y x 22≤+,x y ≤,0y ≥所确定的区域;(2)D 由不等式2222b y x a ≤+≤所确定的区域;(3)D=(){}0x ,y y x y ,x 22≥≤+.7.用极坐标计算二重积分: (1) ⎰⎰+D22dxdy y x sin ,其中D=(){222y x y ,x +≤π }24π≤; (2)()⎰⎰+Ddxdy y x ,其中D=(){}y x y x y ,x 22+≤+; (3)()⎰⎰+'D22dxdy y x f ,其中D 为圆域222R y x ≤+.8.在下列符号分中引入新变量后,试将它化为累次积分:(1) ()⎰⎰--20x 2x 1dy y ,x f dx ,其中u=x+y,v=x-y;(2) ()dxdy y ,x f D⎰⎰,其中D=(){a y x y ,x ≤+,0x ≥, }0y ≥,若x=v cos U 4, v sin U y 4=.(3)()⎰⎰dxdy y ,x f ,其中D=(){a y x y ,x ≤+,0x ≥, }0y ≥,若x+y=u,y=uv.9.求由下列曲面所围立体V 的体积:(1) v 由坐标平面及x=2,y=3,x+y+Z=4所围的角柱体;(2) v 由z=22y x +和z=x+y 围的立体; (3) v 由曲面9y 4x Z 222+=和2Z=9y 4x 22+所围的立体.11.试作适当变换,计算下列积分:(1)()()⎰⎰-+Ddxdy y x sin y x ,D=(){π≤+≤y x 0y .x }π≤-≤y x 0;(2)⎰⎰+D y x y dxdy e,D=(){1y x y ,x ≤+,0x ≥,}0y ≥.12.设f:[a,b]→R 为连续函数,应用二重积分性质证明:()≤⎥⎦⎤⎢⎣⎡⎰2b a dx x f ()()⎰-b a 2dx x f a b ， 其中等号仅在f 为常量函数时成立。

第二十一章 重积分§1 二重积分的概念一 面积 设2D R ⊂是有界闭集，设[,][,]U a b c d D =⨯⊂，在[,]a b 中插入分点01...n a x x x b =<<<=，在[,]c d中插入分点01...n c y y y d =<<<=，过这些分点作平行于坐标轴的直线，将U 分成许多小矩形,11[,][,],1,...;1,...i j i i j j U x x y y i n j m --=⨯==成为U 的一个分划。

记完全包含于D 内的小矩形的面积之和为mA ，与D 交集非空的矩形面积mB ，显然它们与U 分划有关，且有mA mB ≤。

在[,]a b 和[,]c d 中再增加有限个分点（称为加细）则mB 不增，mA 不减，且任一种分化所得到的mA 不大于mB 。

这些mA 的上确界*mD ，mB 的下确界*mD ，且**mD mD ≤。

若**mD mD =，称为D 是可求面积的。

充要条件是*0m D ∂=，边界面积为零的有界闭区域为零边界区域。

光滑曲线段的面积为零。

二 曲顶柱体的体积：底是xy 面具有零边界的有界闭区域D ，顶是非负连续函数(,)z f x y =，(,)x y D ∈所对应的曲面，侧是以D 的边界曲线为准线，母线平行于z 轴的柱面。

三 二重积分的概念：设2D R ⊂是零边界区域，(,)z f x y =在D 上有界。

将D 用曲线网分成n 个小区域，记1max{}i i ndiam D λ≤≤=，01(,)lim (,)niii i DI f x y d f λσξησ→===∑⎰⎰。

设i M 和i m 分别为(,)f x y 在i D 上的上确界与下确界，定义Darboux 大和为1n i i i S M σ==∑，Darboux 小和为1ni i i s m σ==∑性质1 若在已有的份划添加有限条曲线作进一步分划，则Darboux 大和不增，小和不减。

第二十一章 重积分 1二重积分的概念一、平面图形的面积引例：若构成平面图形P 的点集是平面上的有界点集， 即存在矩形R ，使P ⊂R ，则称平面图形P 有界. 用某一平行于坐标轴的一组直线网T 分割P(如图)，这时直线网T 的网眼——小闭矩形△i 可分为三类： (1)△i 上的点都是P 的内点；(2)△i 上的点都是P 的外点，即△i ∩P=Ø； (3)△i 上含有P 的边界点.将所有属于直线网T 的第(1)类小矩形(图中阴影部分)的面积加起来， 记和数为s p (T)，则有s p (T)≤△R (矩形R 的面积)；将所有第(1)类与第(3)类小矩形(图中粗线所围部分)的面积加起来， 记作S p (T)，则有s p (T)≤S p (T). 由确界存在定理知，对于平面上所有直线网，数集{s p (T)}有上确界，数集{S p (T)}有下确界， 记Tp I sup ={s p (T)} ,Tp I inf ={S p (T)}. 显然有0≤p I ≤p I .p I 称为内面积，p I 称为外面积.定义1：若平面图形P 的内面积p I 等于它的外面积p I , 则称P 为可求面积，并称其共同值I p =p I =p I 为P 的面积.定理21.1：平面有界图形P 可求面积的充要条件是：对任给ε>0, 总存在直线网T ，使得S p (T)-s p (T)< ε.证：[必要性]设P 的面积为I p , 由面积的定义知, I p =p I =p I . ∀ε>0, 由p I 及p I 的定义知，分别存在直线网T 1与T 2，使得 s p (T 1)>I p -2ε, S p (T 2)<I p +2ε, 记T 为由T 1与T 2合并所成的直线网，则 s p (T 1)≤s p (T), S p (T 2)≥S p (T)，∴s p (T)>I p -2ε, S p (T)<I p +2ε, 从而S p (T)-s p (T)<ε. [充分性]设对任给的ε>0, 存在某直线网T ，使得S p (T)-s p (T)<ε. 但s p (T)≤p I ≤p I ≤S p (T)，∴p I -p I ≤S p (T)-s p (T)<ε. 由ε的任意性知，p I =p I ，∴平面图形P 可求面积.推论：平面有界图形P 的面积为零的充要条件是它的外面积p I =0，即对任给的ε>0, 存在某直线网T ，使得S p (T)<ε，或 平面图形P 能被有限个其面积总和小于ε的小矩形所覆盖.定理21.2：平面有界图形P 可求面积的充要条件是：P 的边界K 的面积为0.证：由定理21.1，P 可求面积的充要条件是：∀ε>0, ∃直线网T ， 使得S p (T)-s p (T)<ε. 即有S K (T)=S p (T)-s p (T)<ε， 由推论知，P 的边界K 的面积为0.定理21.3：若曲线K 为定义在[a,b]上的连续函数f(x)的图象，则曲线K 的面积为零.证：∵f(x)在闭区间[a,b]上连续，从而一致连续. ∴∀ε>0, ∃δ>0, 当把区间[a,b]分成n 个小区间[x i-1,x i ] (i=1,2,…,n, x 0=a,x n =b)并满足 max{△x i =x i -x i-1 |i=1,2,…,n }<δ时，可使f(x)在每个小区间[x i-1,x i ]上的振幅都有ωi <ab -ε.把曲线K 按自变量x=x 0,x 1,…,x n 分成n 个小段，则 每一个小段都能被以△x i 为宽, ωi 为高的小矩形所覆盖，又 这n 个小矩形面积的总和为i ni i x ∆∑=1ω<ab -ε∑=∆ni ix1<ε，由定理21.1的推论即得曲线K 的面积为零.推论1：参数方程x=φ(t), y=ψ(t), t ∈[α,β]所表示的光滑曲线K 的面积为零.证：由光滑曲线的定义，φ’(t),ψ’(t)在[α,β]上连续且不同时为0. 对任意t 0∈[α,β]，不妨设φ’(t 0)≠0，则存在t ’的某邻域U(t 0), 使得 x=φ(t)在此邻域上严格单调，从而存在反函数t=φ-1(x). 又 由有限覆盖定理，可把[α,β]分成有限段：α=t 0<t 1<…<t n =β， 在每一小区间段上，y=ψ(φ-1(x))或x=ψ(φ-1(y))，由定理21.3知， 每小段的曲线面积为0，∴整条曲线面积为零.推论2：由平面上分段光滑曲线所围成的有界闭区域是可求面积的.注：并非平面中所有的点集都是可求面积的.如D={(x,y)|x,y ∈Q ∩[0,1]}. 易知0=D I ≤D I =1, 所以D 是不可求面积的.二、二重积分的定义及其存在性 引例：求曲顶柱体的体积(如图1).设f(x,y)为定义在可求面积的有界闭区域D 上的非负连续函数. 求以曲面z=f(x,y)为顶，以D 为底的柱体体积V.用一组平行于坐标轴的直线网T 把D 分成n 个小区域σi (i=1,2,…,n). ∵f(x,y)在D 上连续，∴当每个σi 都很小时， f(x,y)在σi 上各点的函数值近似相等； 可在σi 上任取一点(ξi ,ηi )，用以f(ξi ,ηi )为高， σi 为底的小平顶柱体的体积f(ξi ,ηi )△σi 作为V i 的体积△V i ，即△V i ≈f(ξi ,ηi )△σi .把这些小平顶柱体的体积加起来， 就得到曲顶柱体体积V 的近似值： V=∑=∆n i i V 1≈i ni i i f σηξ∆∑=1),(.当直线网T 的网眼越来越细密，即分割T 的细度T =di ni ≤≤1max →0(di 为σi 的直径)时，i ni i i f σηξ∆∑=1),(→V.概念：设D 为xy 平面上可求面积的有界闭区域，f(x,y)为定义在D 上的函数. 用任意的曲线把D 分成n 个可求面积的小区域σ1, σ2,…, σn . 以△σi 表示小区域△σi 的面积，这些小区域构成D 的一个分割T ， 以d i 表示小区域△σi 的直径，称T =di ni ≤≤1max 为分割T 的细度.在每个σi 上任取一点(ξi ,ηi )，作和式ini iif σηξ∆∑=1),(，称为函数f(x,y)在D 上属于分割T 的一个积分和.定义2：设f(x,y)是定义在可求面积的有界闭区域D 上的函数. J 是一个确定的数，若对任给的正数ε，总存在某个正数δ，使对于D 的任何分割T ，当它的细度T <δ时，属于T 的所有积分和都有J f ini ii-∆∑=σηξ1),(<ε，则称f(x,y)在D 上可积，数J 称为函数f(x,y)在D上的二重积分，记作：J=⎰⎰Dd y x f σ),(.注：1、函数f(x,y)在有界可求面积区域D 上可积的必要条件是f 在D 上有界.2、设函数f(x,y)在D 上有界，T 为D 的一个分割，把D 分成n 个可求面积的小区域σ1, σ2,…, σn . 令M i =iy x σ∈),(sup f(x,y), m i =iy x σ∈),(inf f(x,y), i=1,2,…,n.作和式S(T)=i n i i M σ∆∑=1, s(T)=i ni i m σ∆∑=1. 它们分别称为函数f(x,y)关于分割T 的上和与下和.定理21.4：f(x,y)在D 上可积的充要条件是：0lim →T S(T)=0lim →T s(T).定理21.5：f(x,y)在D 上可积的充要条件是：对于任给的正数ε，存在D 的某个分割T ，使得S(T)-s(T)<ε.定理21.6：有界闭区域D 上的连续函数必可积.定理21.7：设f(x,y)在有界闭域D 上有界，且不连续点集E 是零面积集，则f(x,y)在D 上可积.证：对任意ε>0, 存在有限个矩形(不含边界)覆盖了E ，而 这些矩形面积之和小于ε. 记这些矩形的并集为K ，则 D\K 是有界闭域(也可能是有限多个不交的有界闭域的并集). 设K ∩D 的面积为△k ，则△k <ε. 由于f(x,y)在D\K 上连续， 由定理21.6和定理21.5，存在D\K 上的分割T 1={σ1, σ2,…, σn }, 使得S(T 1)-s(T 1)<ε. 令T={σ1, σ2,…, σn , K ∩D}，则T 是D 的一个分割，且 S(T)-s(T)=S(T 1)-s(T 1)+ωK △k <ε+ωε, 其中ωK 是f(x,y)在K ∩D 上的振幅，ω的是f(x,y)在D 上的振幅. 由定理21.5可知f(x,y)在D 上可积.三、二重积分的性质1、若f(x,y)在区域D 上可积，k 为常数，则kf(x,y)在D 上也可积，且⎰⎰Dd y x kf σ),(=k ⎰⎰Dd y x f σ),(.2、若f(x,y), g(x,y)在D 上都可积，则f(x,y)±g(x,y)在D 上也可积，且[]⎰⎰±Dd y x g d y x f σσ),(),(=⎰⎰Dd y x f σ),(±⎰⎰Dd y x g σ),(.3、若f(x,y)在D 1和D 2上都可积，且D 1与D 2无公共内点，则⎰⎰21),(D D d y x f σ=⎰⎰1),(D d y x f σ+⎰⎰2),(D d y x f σ.4、若f(x,y)与g(x,y)在D 上可积，且f(x,y)≤g(x,y), (x,y)∈D ，则⎰⎰Dd y x f σ),(≤⎰⎰Dd y x g σ),(.5、若f(x,y)在D 上可积，则函数|f(x,y)|在D 上也可积，且⎰⎰Dd y x f σ),(≤⎰⎰Dd y x f σ),(.6、若f(x,y)在D 上都可积，且m ≤f(x,y)≤M, (x,y)∈D ，则 mS D ≤⎰⎰Dd y x f σ),(≤MS D , 其中S D 是积分区域D 的面积.7、(中值定理)若f(x,y)在有界闭区域D 上连续，则存在(ξ,η)∈D ， 使得⎰⎰Dd y x f σ),(=f(ξ,η)S D , 其中S D 是积分区域D 的面积.注：中值定理的几何意义：以D 为底，z=f(x,y) (f(x,y)≥0)为曲顶的曲顶柱体体积等于一个同底的平顶柱体的体积，这个平顶柱体的高等于f(x,y)在区域D 中某点(ξ,η)的函数值f(ξ,η).习题1、把重积分⎰⎰Dxydxd σ作为积分和的极限，计算这个积分值，其中D=[0,1]×[0,1]，并用直线网x=n i, y=nj , (i,j=1,2,…,n-1)分割D 为许多小正方形，每个小正方形取其右顶点作为其节点.解：⎰⎰Dxydxd σ=2111lim n n j n i nj ni n ⋅⋅∑∑==∞→=21121lim n n j n nj n ⋅⋅+∑=∞→=224)1(lim n n n +∞→=41.2、证明：若函数f(x,y)在有界闭区域D 上可积，则f(x,y)在D 上有界. 证：若f 在D 上可积，但在D 上无界，则对D 的任一分割T={σ1, σ2,…, σn }, f 必在某个小区域σk 上无界. 当i ≠k 时，任取p i ∈σi ，令G=∑≠nki i i p f σ)(, I=⎰⎰Ddxdy y x f ),(.∵f 在σk 上无界，∴存在p k ∈σk ，使得|f(p k )|>kG I σ∆++1, 从而∑=ni iip f 1)(σ=∑≠∆+nki k k i i p f p f σσ)()(≥|f(p k )·△σk |-∑≠nki i i p f σ)(>|I|+1.又f 在D 上可积，∴存在δ>0，对任一D 的分割T={σ1, σ2,…, σn }, 当T <δ时，T 的任一积分和∑=nk k k p f 1)(σ都满足∑=-nk k k I p f 1)(σ<1,即∑=nk k k p f 1)(σ<|I|+1，矛盾！∴f 在D 上可积，则f 在D 上有界.3、证明二重积分中值定理：若f(x,y)在有界闭区域D 上连续，则存在(ξ,η)∈D ，使得⎰⎰Df =f(ξ,η)S D , 其中S D 是积分区域D 的面积.证：∵f 在有界闭区域D 上连续,∴f 在D 上有最大值M 和最小值m, 对D 中一切点有m ≤f ≤M ，∴mS D ≤⎰⎰Df ≤MS D , 即m ≤⎰⎰DDf S 1≤M.由介值性定理知，存在(ξ,η)∈D ，使得⎰⎰Df =f(ξ,η)S D .4、证明：若f(x,y)为有界闭区域D 上的非负连续函数，且在D 上不恒为零，则⎰⎰Dd y x f σ),(>0.证：由题设知存在p 0(x 0,y 0)∈D ，使f(p 0)>0，令δ=f(p 0)，由连续函数的局部保号性知：∃η>0使得对一切p ∈D 1(D 1=U(p 0,η)∩D), 有f(p)>2δ. 又f(x,y)≥0且连续，∴⎰⎰Df =⎰⎰1D f +⎰⎰-1D D f ≥2δ·△D 1>0.5、证明：若f(x,y)在有界闭区域D 上连续，且在D 内任一子区域D ’⊂D 上有⎰⎰'D d y x f σ),(=0，则在D 上f(x,y)≡0.证：假设存在p 0(x 0,y 0)∈D ，使得f(p 0)≠0, 不妨设f(p 0)>0. 由连续函数的保号性知，∃η>0使得对一切p ∈D ’(D ’=U(p 0,η)∩D), 有f(p)>0，由第4题知⎰⎰'D f >0，矛盾！ ∴在D 上f(x,y)≡0.6、设D=[0,1]×[0,1]，证明： 函数f(x,y)=⎩⎨⎧内非有理点为皆为有理数即内有理点为D y x y x D y x ),(,0),(),(,1在D 上不可积.证： 设D 的任一分割T={σ1, σ2,…, σn }, 则每一个小区域σi 内必同时含有D 内有理点和非有理点，从而 M i =iy x σ∈),(sup f(x,y)=1, m i =iy x σ∈),(inf f(x,y)=0, i=1,2,…,n.∴S(T)=i n i i M σ∆∑=1=1, s(T)=i ni i m σ∆∑=1=0，由T 的任意性知：lim →T S(T)=1≠0=0lim →T s(T). ∴f 在D 上不可积.7、证明：若f(x,y)在有界闭区域D 上连续，g(x,y)在D 上可积且不变号，则存在一点(ξ,η)∈D ，使得⎰⎰Dd y x g y x f σ),(),(=f(ξ,η)⎰⎰Dd y x g σ),(.证：不妨设g(x,y)≥0, (x,y)∈D ，则⎰⎰Dd y x g σ),(≥0. 令M,m 分别为f 在D 上的最大、最小值，则 m ⎰⎰Dd y x g σ),(≤⎰⎰Dd y x g y x f σ),(),(≤M ⎰⎰Dd y x g σ),(.若⎰⎰Dd y x g σ),(=0, 则⎰⎰Dd y x g y x f σ),(),(=0，任取(ξ,η)∈D ，得证！若⎰⎰Dd y x g σ),(>0, 则m ≤⎰⎰⎰⎰DDd y x g d y x g y x f σσ),(),(),(≤M. 由介值性定理知，存在一点(ξ,η)∈D ，使得f(ξ,η)=⎰⎰⎰⎰DDd y x g d y x g y x f σσ),(),(),( ，即⎰⎰Dd y x g y x f σ),(),(=f(ξ,η)⎰⎰Dd y x g σ),(.8、应用中值定理估计积分：I=⎰⎰++Dyx d 22cos cos 100σ的值, 其中D={(x,y)||x|+|y|≤10}. 解：∵f(x,y)=yx 22cos cos 1001++ 在D={(x,y)||x|+|y|≤10}上连续，根据中值定理知：存在(ξ,η)∈D ，使得I=ηξ22cos cos 100++∆D, 从而102D ∆≤I ≤100D ∆, △D 为D 的面积，∴51100≤I ≤2.9、证明：若平面曲线x=φ(t), y=ψ(t), α≤t ≤β光滑 (即φ(t),ψ(t)在[α,β]上具有连续导数且φ’2(t)+ψ’2(t)≠0)，则 此曲线的面积为0.证法1：该平面曲线L 的长度为l=dt t t ⎰'+'βαψϕ)()(22为有限值.对∀ε>0, 将L 分成n=⎥⎦⎤⎢⎣⎡εl +1段：L 1,L 2,…,L n , 在每段L i 上取一点P i , 使P i 与其一端点的弧长为nl 2，以P i 为中心作边长为的ε正方形△i ， 则L i ⊂△i (i=1,2,…,n), 从而L ⊂n i 1= △i ，记△=ni 1= △i ，则△为一多边形.设△的面积W ，则W ≤n ε2=⎪⎭⎫ ⎝⎛+1εlε=(1+ε)ε，∴L 的面积W L ≤W ≤(1+ε)ε. 即此曲线的面积为0.证法2：在曲线上任取参数t 的点M ，∵φ’2(t)+ψ’2(t)≠0， 由隐函数存在定理知，存在σ=(t-δ,t+δ)使曲线上对应的一段可以表示成显式方程.应用有限覆盖定理，[α,β]被开区间集{σ}有限覆盖，得出有限个区间， 使曲线分成有限部分，每一部分可以表示成显式方程y=f(x)或x=g(y)， 其中f,g 为连续函数，由定理21.3知光滑曲线的面积为0.。

第二十一章 重积分§1二重积分概念1.把重积分Dxyd s 蝌作为积分和的极限，计算这个积分值，其中[0,1][0,1]D =?并用直线网,(,1,2,1)i ix y i j n n n===-分割这个正方形为许多小正方形，每一小正方形取其右上顶点为其节点。

证明：22n 24i=1j=111(1)1lim lim 44n xx Di j n n xydxdy n n n n +=鬃==邋蝌2.证明：若函数(,)f x y 在有界闭区域D 上可积，则(,)f x y 在D 上有界。

证明：假设(,)f x y 在D 上可积，但在D 上无界。

则对D 的任一分割T={}n 12s ,s ,s ,(,)f x y 必在某个小区间k s 上无界。

当i k ¹时，任取i i p 蝧，令G=(),(,),i i i kDf p I f x y dxdy ¹s =å蝌由于(,)f x y 在k s 上无界，即存在k k p 蝧使得1()k kI Gf p ++>s 。

从而1()())()()()2 1.(*)nii i i k k k ki k i i ki kf p f p f p f p f p =构s =s +s 硈-s >+邋?另一方面，由于(,)f x y 在D 上可积，取1e =，故存在0d >，对任意D 的分割n {}T 12=s ,s ,s 当T <δ时，i 1i=11*f x y D nT I ¹-<ååni i i i 的任一分f(p σ)都满足f(p )σ而（）式与此矛盾，所以，(,)在上有界3.证明二重积分中值定理（性质7）。

证明：函数(,)f x y 在有界闭区域D 上连续，则(,)f x y 在D 上存在最大值M 与最小值m ，且对D 中一切(,)x y 点，有(,).m f x y M ＃ 有性质6知，,(,)D D DmS f x y d MS ££蝌σ即1(,)DDm f x y d M S ＃蝌σ有介值定理存在()D Îξ,η使得(,).()Df x y d f D S =蝌σξ,η4：若(,)f x y 为有界闭区域D 上的非负连续函数，且在D 上不恒为零，则(,)0Df x y d >蝌σ证明：由已知，存在000(,)p x y D Î，使00(,)0f x y >则存在0>δ，对一切1(,)p x y D Î，其中10,(())D P D =?δ，有001(,)(,)02f x y f x y >> 而(,)f x y 在有界闭域D 上非负连续，则有111001(,)(,)(,)(,)02D D D D Df x y d f x y d f x y d f x y S -=+?蝌蝌蝌σσσ 其中（1D S 表示为1D 的面积）5.若(,)f x y 在有界闭区域D 上连续，且在D 内任一子区域'D D Ì上有'(,)0D f x y d=蝌σ 则在D 上(,)0.f x y º证明：用反证法：假设在D 内存在一点000(,)p x y 使00(,)0f x y ¹，不妨设00(,)0f x y >。