第09章组合变形题解
- 格式:doc
- 大小:528.04 KB
- 文档页数:9





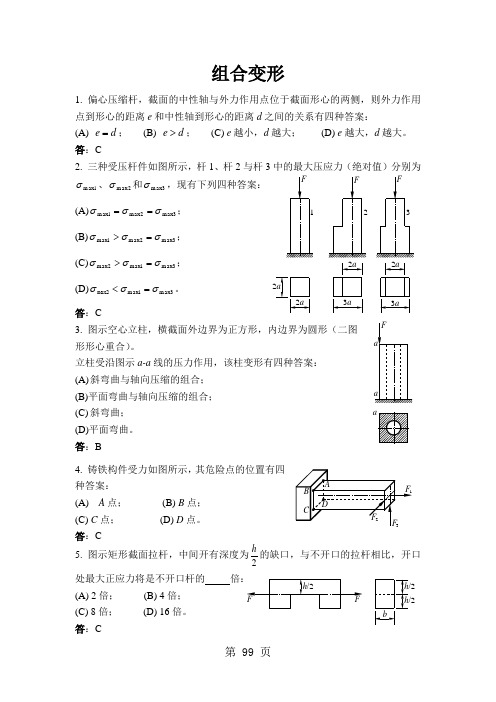
组合变形1. 偏心压缩杆,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到形心的距离e 和中性轴到形心的距离d 之间的关系有四种答案: (A) d e =; (B) d e >; (C) e 越小,d 越大; (D) e 越大,d 越大。
答:C2. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为1m ax σ、2m ax σ和3m ax σ,现有下列四种答案: (A)3max 2max 1max σσσ==; (B)3max 2max 1max σσσ=>; (C)3max 1max 2max σσσ=>; (D)3max 1max σσσ=<max2。
答:C3.形形心重合)。
立柱受沿图示a-a (A) 斜弯曲与轴向压缩的组合; (B)平面弯曲与轴向压缩的组合; (C) 斜弯曲; (D)平面弯曲。
答:B4. 铸铁构件受力如图所示,种答案:(A) A 点; (B) B 点; (C) C 点; (D) D 点。
答:C5. 图示矩形截面拉杆,中间开有深度为2h的缺口,与不开口的拉杆相比,开口处最大正应力将是不开口杆的 倍:(A) 2倍; (B) 4倍; (C) 8倍; (D) 16倍。
答:C6. 三种受压杆件如图所示,杆1、杆2与杆3中的最大压应力(绝对值)分别为1m ax σ、2m ax σ和3m ax σ(A)max32max 1max σσσ<<; (B)3max 2max max1σσσ=<; (C)2max max3max1σσσ<<; (D)2max 3max 1max σσσ<=。
答:C 7. 正方形等截面立柱,受纵向压力作用。
当力F 点由A 移至B 时,柱内最大压应力的比值maxmaxB A σσ有四种答案:(A) 1:2; (B) 2:5; (C) 4:7; (D) 5:2。
答:C8. 图示矩形截面偏心受压杆,其变形有下列四种答案: (A) 轴向压缩和平面弯曲的组合; (B)轴向压缩、平面弯曲和扭转的组合; (C)缩和斜弯曲的组合;(D)轴向压缩、斜弯曲和扭转的组合。
第九章组合变形 9–1概述一、组合变形 :在复杂外载作用下,构件的变形会包含几种简单变形,当几种变形所对应的应力属同一量级时,不能忽略之,这类构件的变形称为组合变形。
二、组合变形的研究方法——叠加原理①外力分析:外力向形心(或弯心)简化并沿形心主惯性轴分解。
②内力分析:求每个外力分量对应的内力方程和内力图,确定危险面。
③应力分析:画危险面应力分布图,叠加,建立危险点的强度条件。
9–2斜弯曲一、斜弯曲:杆件产生弯曲变形,但弯曲后,挠曲线与外力(横向力)不共面。
二、斜弯曲的研究方法:1.分解:将外载沿横截面的两个形心主轴分解,于是得到两个正交的平面弯曲。
2.叠加:分别对两个平面弯曲进行研究;然后将计算结果叠加起来。
解:1.将外载沿横截面的形心主轴分解ϕsin P P y =ϕcos P P z =2.研究两个平面弯曲 ①内力ϕϕsin sin M Px x P M y z === ϕϕcos cos M Py x P M x y ===M y 引起的应力:ϕσcos yyy I M I z M z-=-=' M z 引起的应力:ϕσsin zz z I M I y M y-=-='' 自:注意这里M y M z 所取的惯性矩是不同的。
合应力:)sin cos (ϕϕσσσzy I yI z M +-=''+'=③中性轴方程0)sin cos (00=+-=ϕϕσzy I yI z M ϕαctg tg 00yzI I z y ==④最大正应力在中性轴两侧,距中性轴最远的点为拉压最大正应力点。
2max D L σσ=1max D y σσ=⑤变形计算22z y f f f +=,zy f f =βtg(自:横:123bh I z =竖:123hb I y =)(自:收均布载荷简支梁:82maxql M =)9–3拉(压)弯组合 偏心拉(压)截面核心一、拉(压)弯组合变形:杆件同时受横向力和轴向力的作用而产生的变形。
第六章直梁弯曲弯曲变形是杆件比较常见的基本变形形式。
通常把以发生弯曲变形为主的杆件称为梁。
本章主要讨论直梁的平面弯曲问题,内容包括:弯曲概念和静定梁的力学简图;弯曲内力及内力图;弯曲应力和强度计算;弯曲变形和刚度计算。
其中,梁的内力分析和画弯矩图是本章的重点。
第一节平面弯曲的概念和力学简图一、弯曲概念和受力特点当杆件受到垂直于杆轴的外力作用或在纵向平面内受到力偶作用(图6-1)时,杆轴由直线弯成曲线,这种在外力作用下其轴线变成了一条曲线。
这种形式的变形称为弯曲变形。
工程上通常把以弯曲变形为主的杆件称为梁。
图 6-1 弯曲变形是工程中最常见的一种基本变形。
例如房屋建筑中的楼面梁和阳台挑梁,受到楼面荷载和梁自重的作用,将发生弯曲变形,如图6-2所示。
一些杆件在荷载作用下不仅发生弯曲变形,还发生扭转等变形,当讨论其弯曲变形时,仍然把这些杆件看做梁。
图6-2工程实际中常见到的直梁,其横截面大多有一根纵向对称轴,如图6-3所示。
梁的无数个横截面的纵向对称轴构成了梁的纵向对称平面,如图6-4所示。
图 6-3 图6-4若梁上的所有外力(包括力偶)作用在梁的纵向对称平面内,梁的轴线将在其纵向对称平面内弯成一条平面曲线,梁的这种弯曲称为平面弯曲,它是最常见、最基本的弯曲变形。
本章主要讨论直梁的平面弯曲变形。
从以上工程实例中可以得出,直梁平面弯曲的受力与变形特点是:外力作用于梁的纵向对称平面内,梁的轴线在此纵向对称面内弯成一条平面曲线。
二、梁的受力简图为了便于分析和计算直梁平面弯曲时的强度和刚度,需建立梁的力学简图。
梁的力学简图(力学模型)包括梁的简化、荷载的简化和支座的简化。
1、梁的简化由前述平面弯曲的概念可知,载荷作用在梁的纵向对称平面内,梁的轴线弯成一条平面曲线。
因此,无论梁的外形尺寸如何复杂,用梁的轴线来代替梁可以使问题得到简化。
例如,图6-1a和图6-2a所示的火车轮轴和桥式起重机大梁,可分别用梁的轴线AB代替梁进行简化(图6-1b和图6-2b)。
第 9 章 组 合 变 形9-1 试分析下列构件在指定截面A 的内力分量(判断基本变形)解:(a )拉伸与弯曲;(b )压缩、扭转与两个方向的弯曲; (c )压缩、扭转与两个方向的弯曲。
9-2 木制矩形截面悬臂梁受力如图,已知 F 1 = 0.8 kN ,F 2 = 1.65 kN ,木材的许用应力 [ σ ] =10 MPa ,若矩形 h /b = 2 ,试确定其截面尺寸。
解:显然固定端是危险截面。
kNm 6.128.01=⨯==l F M ykNm 65.1165.122=⨯==lF M z =+=+=22max 66bh M hb M W M W M zy z z y yσ][)233(13σ≤+=z y M M b 代入数据得到363mm 727500101065.15.16.13=⨯⨯+⨯≥b , mm 180h ,mm 90≥≥b 。
9-3 工字钢简支梁受力如图,已知 F = 7 kN ,[ σ ] =160 MPa ,试选择工字钢型号。
(提示:先假定 W z /W y 的比值进行试选,然后校核。
) 解:显然中间截面是危险截面。
kNm 741max ==l F M kNm 394.220sin max == M M y , kNm 578.620cos max == M M z(b )车刀 (a )机械构件][max σσ≤+=zzyy W M W M 选 6=y z W W 试算 33cm 8.21101606394.26578.6][66=⨯⨯⨯+=+≥σyz y M M W查表取 16 号工字钢 W y = 21.2 cm 3 ,W z = 141 cm 3 校核强度 ][M Pa 15910)2.21394.2141578.6(3max σσ≤=⨯+=+=z z yy W M W M 强度刚好够,所以选定 16 号工字钢。
9-4 证明斜弯曲时横截面仍然绕中性轴转动(提示:证明截面形心位移垂直于中性轴)。
证明:假设在任意相距很近 dx 的截面之间作用两个M y ,M z ,其中下标 y ,z 为截面形心主惯性轴,中性轴方程由0=-=y I M z I M z z yy σ 确定为 ϕtan ==yz zy I M I M z y 两截面之间由M z 和M y 产生的相对位移分别为2)(dx EI M dx d Y z z z =⋅=θ,2)(dx EI M dx d Z y y y -=⋅=θ,tan =-=zy yz I M I M Z Y 显然tan α tan ϕ = -1 ,α = ϕ±90°即截面形心位移与中性轴互相垂直。
[反证法] 假设斜弯曲时横截面绕非中性轴转动,则中性轴上的纵向纤维将有伸长或缩短,这与斜弯曲时横截面存在有中性轴的结论是相矛盾的。
故斜弯曲时横截面绕中性轴转动。
9-5 证明对正多边形截面梁,横向力无论作用方向如何偏斜,只要力的作用线通过截面形心,都只产生平面弯曲。
证明:只要证明任意正多边形的形心坐标轴为形心主惯轴即可。
现以正三角形为例,图中y 、z 轴为一对正交形心主轴,y 和y 1轴为对称轴,显然,I y = I y 1,I yz = 0;由式(A-13)有β2cos 221yz y z y y I I I I I I -++== 即z y y z yz I I I I I I =⇒=-⇒=--00)2cos 1(2β设Y 、Z 为一对任意正交形心轴,由式(A-15)有 02cos 2sin 2=+-=ααyz yz YZ I I I I即任意形心轴都是主惯性轴,其惯性矩都相等,只可能发生平面弯曲,不会发生斜弯曲。
z9-6 求图示正六边形截面悬臂梁的最大应力。
(已知正六边形的形心主惯性矩 I y = I z )解:显然 固定端是危险截面,l F M =m a x由于正六边形的形心主惯性矩 I y = I z ,只发生平面弯曲,中性轴与载荷作用线垂直,外凸角点中距离中性轴最远的点是A 点,如图(a )所示,A 点到中性轴的距离15cos a h = , 15cos max a I lF z =σ9-7 图示起重架的最大起吊重量(包括小车)为 F = 40 kN ,横梁 AB 由两根 18 号槽钢组成,[ σ ] =120 MPa ,试校核横梁强度。
解:以小车行至横梁中央作为危险工况,此时最大弯矩在梁的中间截面 C , 最大弯矩 kNm 354==l F M C ,轴向压力 kN 64.3423==F F x AB 梁发生压缩与弯曲组合变形 AFW M x z C +=max σ查表得 18 号槽钢 3cm 2.152=z W ,2cm 29.29=A 代入上式MPa 9.1209.51151029.29264.34102.1522353max =+=⨯⨯+⨯⨯=σ略大于许用应力,一般情况下可以安全使用。
9-8 拆卸工具的勾爪受力如图,已知两侧爪臂截面为矩形,[ σ ] =180 MPa ,试按爪臂强度条件确定拆卸时的最大顶力 F 。
解:勾爪立柱发生拉伸与弯曲组合变形2F N = , 2Fe M =M Pa 180][)261732626171(2)61(222max =≤⨯⨯+⨯==+=+=σσF bhe h b F W M A N z解得 F = 19 kN 。
9-9 压力机框架为铸铁材料,[ σ+ ] = 30MPa ,[ σ-] = 80 MPa ,立柱截面尺寸如图所示,试校核框架立柱的强度。
解:截面形心(a )A -A 剖面mm 5.40420017200050202060100209020505020601010020==⨯+⨯+⨯⨯⨯+⨯⨯+⨯⨯=c z4232323cm 4885.49205020501215.9602060201215.302010020100121=⨯⨯+⨯⨯++⨯⨯+⨯⨯+⨯⨯+⨯⨯=yc I截面内力 kN 12==F N , kNm 89.2)0405.02.0(12)(=+⨯=+=c z a F MMPa 9.2686.22410420012105.4048889.232max =+=⨯+⨯⨯=+σ MPa 3.3286.22.3510420012105.5948889.232max -=+-=⨯+⨯⨯-=-σ 9-10 图示矩形截面杆偏心受拉,由实验测得两侧的纵向应变 ε1 和ε2 ,试求偏心距 e 。
解:试件发生偏心拉伸 F N = , Fe M =两测点应变分别为E bh Fe bhEF 2216±=εε , b h E F 221=+εε , Ebh Fe 22112=-εε 联立求解可得 62121he εεεε+-=9-11 求图示矩形截面立柱固定端 A ,B ,C ,D 四点的正应力,并确定中性轴的位置。
解:立柱发生压缩与弯曲组合变形,危险截面在固定端kN 25-=N , kNm 36.05=⨯=y M ,kNm 25.105.025=⨯=z M362mm 105.13.01.061⨯=⨯⨯=y W 362mm 105.01.03.061⨯=⨯⨯=z W483mm 1025.23.01.0121⨯=⨯⨯=y I 483mm 1025.01.03.0121⨯=⨯⨯=z I ,A = 0.1×0.3 = 3×104 mm 2 M Pa 67.3=++=A N W M W M y y z z Aσ , M Pa 33.0-=+-=AN W M W M y y z z B σ M P a 33.5-=+--=A N W M W M y y z z C σ , M Pa 33.1-=++-=AN W M W My y z z D σ 中性轴方程为2ε1030010010251025.21031025.01025.138686=⨯⨯-⨯⨯-⨯⨯=+-=z y A N z I M y I M y y z z σ 整理化简可得 250415=-z y9-12 确定图9-12所示矩形截面和圆形截面的截面核心大小。
解:由式(9-9),对矩形⇒±=-=22he i a y z y 6122223hbh bh hA I e z y === 同理可得 6b e z= 对圆形 ⇒±=-=R e i a 2 4RAa I e ==9-13 电动机工作时的最大转矩 T = 120 N ·m ,主轴 l = 120 mm ,d = 40 mm ,皮带轮直径 D = 250 mm ,皮带张力 F 1 = 2 F 2 ,[ σ ] = 60 MPa ,用第三强度理论校核该主轴强度。
解:由力偶矩平衡 T DF D F F ==-22)(221 N 96025.0120222=⨯==D T F ,N 28803221==+=F F F F 显然轴的根部是危险截面 Nm 6.34512.02880=⨯==l F M ,Nm 120==T M nMPa 5810401206.345323322223=⨯+=+=πσznr W M M 强度足够。
9-14 图示皮带轮传动轴尺寸及受力已知,[ σ ] = 80 MPa ,按第四强度理论选择轴的直径 d 。
解:(1)作轴的受力简图如图(a )所示;F = 14 kN , T = 1.5 kNm(b )M(a)(2)作轴的扭矩图、弯矩图如图(b )、(c )、(d )所示;由图中可以看出 B 截面是危险截面,该截面的弯矩为My = 2.8 kNm , Mz = 1.4 kNm (3)危险点的相当应力 ][75.02224σσ=++=znz y r W M M M62223108014.35.175.04.18.232⨯⨯⨯++=d 解得 d = 75.6 mm 。
9-15 钢制圆轴在齿轮 B ,C 上受力如图所示, 已知 [ σ ] = 100 MPa ,按第四强度理论确定该齿轮轴的直径。
解:(1) 作轴的受力简图如图(a )所示; F 1= 5 kN , F 2= 10 kN , T = 0.75 kNm(2) 作轴的扭矩图、弯矩图如图(b )(c )(d )所示;由图中可以看出 C 截面是危险截面,该截面的弯矩为My = 1.125 kNm , Mz = 0.188 kNm(3) 危险点的相当应力 ][75.02224σσ≤++=znzyr W M M M622231010014.375.075.0188.0125.132⨯⨯⨯++=d 解得1.51=d 9-16牙轮钻杆外径 D = 152 mm 内径d = 120 mm ,钻进压力F = 180 kN ,扭矩T = 17.3 kN ·m,[ σ ] = 100 MPa ,按第四强度理论校核钻杆强度。