02第三节时距曲线之多层介质反射波时距曲线
- 格式:ppt
- 大小:1.03 MB
- 文档页数:43

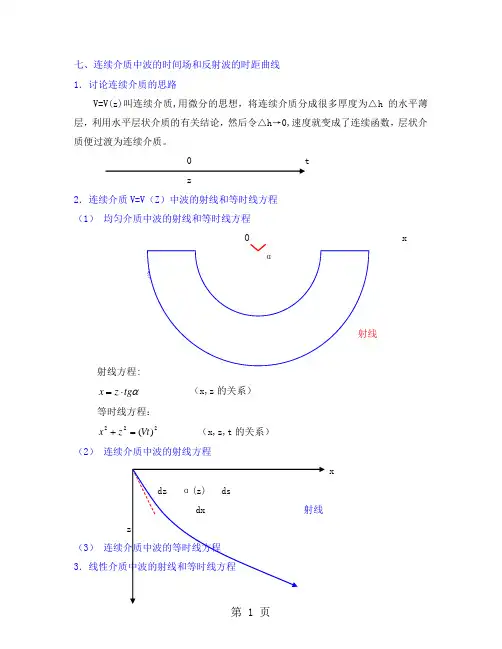
七、连续介质中波的时间场和反射波的时距曲线1.讨论连续介质的思路V=V(z)叫连续介质,用微分的思想,将连续介质分成很多厚度为△h的水平薄层,利用水平层状介质的有关结论,然后令△h→0,速度就变成了连续函数,层状介质便过渡为连续介质。
0 tz2.连续介质V=V(Z)中波的射线和等时线方程(1)均匀介质中波的射线和等时线方程射线方程αx⋅=(x,z的关系)ztg等时线方程:2)22+(x,z,t的关系)x=z(Vt(2)连续介质中波的射线方程(3)3(1) 射线方程将)1(0z V V β+=代入)342.6('-,得0α——射线在震源处与Z 轴的夹角。
华北地区0V =1810m/sβ=0.00026/m特点:线性介质中波的射线是圆弧,圆心在Z=-β1直线上变动提问:①波在线性介质中走什么样的路径?波从O →B 是走直线吗?②波在线性介质中的等时线是什么样的?与均匀介质中的情况比较。
4.线性连续介质中的直达波和反射波h),(''t x P C V =2 R zP58 图6.2-12为什么反射波上下路径对称?(1)直达波(回折波)——指波从震源发出没有碰上界面的作用,直接传播到地面的波,因波线是圆弧,故线性介质中的直达波又叫回折波,每条射线都有一处穿透深度最大。
当h Z ≤max 时,形成回折波。
当h Z ≥max 时,形成反射波。
max Z ——最大穿透深度。
h ——界面的埋深。
(2)回折波的时距曲线方程将观测线方程z=0代入等时线方程(6.2-37)中,得 ⎥⎦⎤⎢⎣⎡+=121220x ch arc V t ββ P58 (3) 反射波的时距曲线将观测线方程z=h 代入等时线方程(6.2-37)中,得到波从O →),(''t x P 用时't 与'x 的关系:再将''22t t x x ==代入上式,得波从O →P →G 的用时t 与x 的关系,即时距曲线: (4) 时距曲线的特点①只在OA 内才能收到反射波和回折波。





第二章 地震波的时距曲线在地震勘探工作中,每激发一次人工地震,都要在多个检波点接收地震信号。
炮点和检波点都沿一条直测线布置,炮点到任意检波点的距离称炮检距x ,相邻检波点的距离叫道间距Δx ,来自同一界面的地震波沿不同路径先后到达各检波点,从而形成一张如图所示的地震记录。
图中横坐标表示地震波旅行时间t ,纵坐标表示炮点到任意检波点的距离称炮检距x ,每一条波动曲线是一道地震记录,它反映出一个检波点的振动过程。
来自同一界面的反射波(或折射波)以一定的视速度规律依次到达个检波点,在地震记录中表现为振动极值的规则排列,各道地震记录波按一定规则排列,形成同相轴(它是相同相位点的连线形成的图形)。
同相轴反映出地震波的旅行时间t 与炮检距x 的函数关系。
将它表示在t-x 直角坐标系中,称为地震波的时距曲线。
不同种类的地震波,其时距曲线的形状不同。
如图中的直达波、反射波、折射波、地滚波、声波等都有自己特有的形状。
每一类特定的时距曲线,其曲线参数与地下介质的纵波速度v 及地震界面的产状有着直接的关系。
第一节 反射波的时距曲线一、 两层介质的直达波和反射波时距曲线(一)直达波的时距曲线从震源出发,不经过反射或折射而直线前进到各检波点的地震波成为直达波。
当震源深度为零时,直达波沿测线传播,旅行时间t 与炮检距x 的函数关系为)1.1.2(1v x t ±= 是两条经过原点的、斜率为1/v 1的两条直线。
如图2.1-1,根据直达波时距曲线的斜率,可以求取界面上层介质的波速v 1。
图2.1-1 直达波与水平界面反射波时距曲线(二)水平界面的反射波时距曲线和正常时差由图2.1-1,若界面埋深为h, 炮点0为激发点,到达界面R 点后反射到地面的s 点,设s 点的炮检距为x ,为计算方便,做炮点0关于界面的镜像点0*,称为虚震源,根据图2.1-1的几何关系,反射波旅行时间t 与炮检距x 的函数关系为)2.1.2(4102211*x h v v RS t +== 将反射波在炮点的反射时间称为反射回声时间,102v h t = 则(2.1.1)式可改写为)2.1.2()(2122022120′+=+=v x t t v x t t 或 式(2.1.2)就是水平界面反射波的时距曲线,可化简为以下的标准双曲线方程)2.1.2(1422202′′=−h x t t综上所述:1.反射波时距曲线在x-t 坐标系是双曲线,其极小点在炮点正上方;2.在x 2-t 2坐标系,反射波时距曲线是直线,直线的斜率为1/v 12, 利用直线的斜率可求界面上方介质的速度;3.反射波时距曲线以直达波时距曲线为其渐近线。

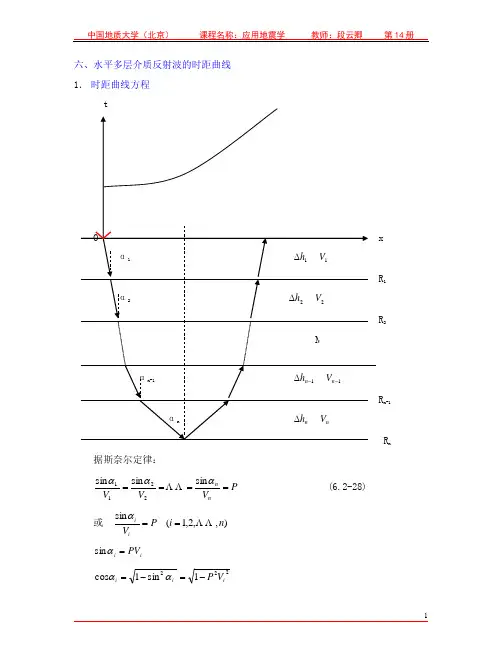
六、水平多层介质反射波的时距曲线 1. 时距曲线方程1 2 n-1 n 据斯奈尔定律:P V V V nn ====αααsin sin sin 2211 (6.2-28) 或),,2,1(sin n i P V ii==α i i PV =αsin2221sin 1cos i i i V P -=-=αα设波在第n 个界面上发生反射,波在水平层状介质中应走折线。
则[]22211⨯∆++∆+∆=n n tg h tg h tg h x ααα∑∑==-∆=∆=ni ii i ni i i i V P PV h h 122112cos sin 2αα∑∑∑===-∆=∆=⋅∆==⨯+++=ni i i iiii i ni i i n i ii n n V P V h h S V h V S V S V S V S t 12211221112)cos (1cos 222][αα⎪⎪⎩⎪⎪⎨⎧-∆=-∆=∑∑==ni i i i ni i i i V P V h t V P PV h x 1221221212 P55(§6.2-28①) 特点:①不是双曲线,②显函数形式写不出来。
2. 平均速度V(1) 平均速度的概念:① 波的射线速度V r ——波沿着射线的平均速度 nn nn n r V S V S V S S S S t t t S S S V ++++++=++++++=2211212121n n n nn V h V h V h h h h ααααααcos cos cos cos cos cos 2221112211∆++∆+∆∆++∆+∆=P54(§6.2②)② 平均速度的第一种定义方法当波垂直入射时,有021====n ααα ,P54(§6.2②)式变成:nn n V h V h V h h h h V 0cos 0cos 0cos 0cos 0cos 0cos 221121∆++∆+∆∆++∆+∆=∑∑∑∑====∆=∆∆=∆++∆+∆∆++∆+∆=ni ini ini ii ni inn nthV h hV h V h V h h h h 1111221121 P54(§6.2③)波在水平层状介质中垂直传播的总路程与总时间之比叫平均速度。
