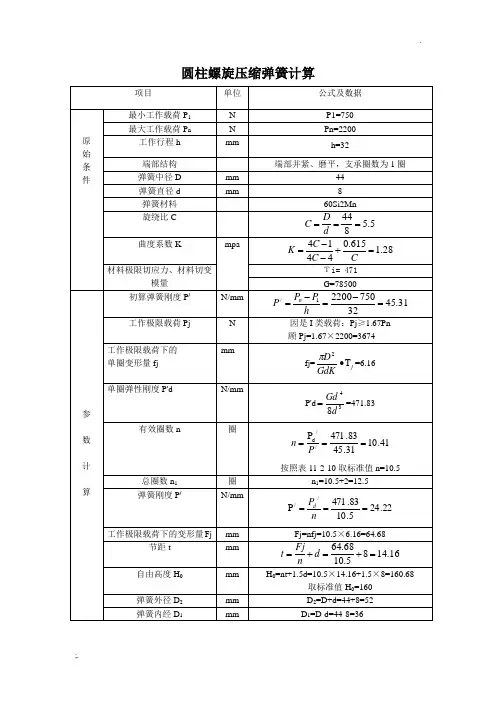
螺旋弹簧数据计算
- 格式:xlsx
- 大小:13.72 KB
- 文档页数:2
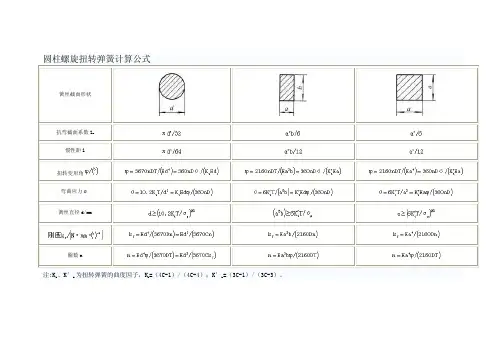
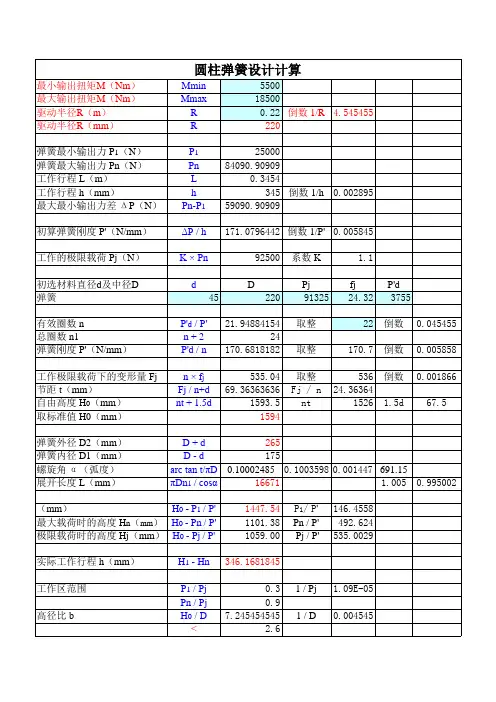
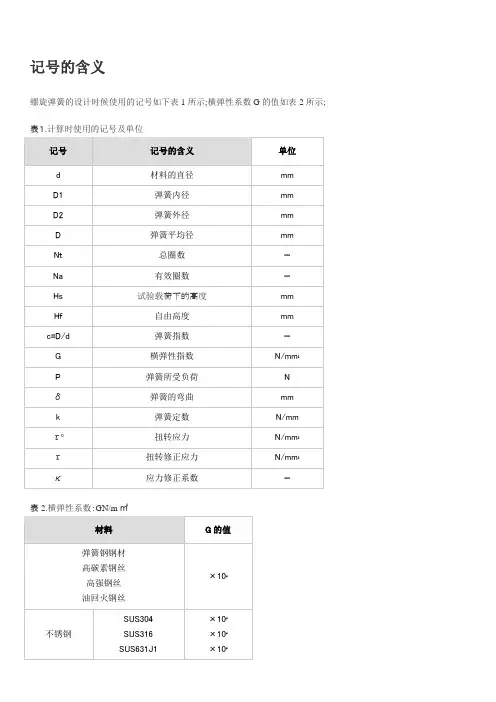
记号的含义螺旋弹簧的设计时候使用的记号如下表1所示;横弹性系数G的值如表2所示; 表1.计算时使用的记号及单位表2.横弹性系数:GN/m㎡螺旋弹簧的设计用基本计算公式螺旋弹簧的负荷和弹簧定数弯曲的关系具有线性特征弹簧的负荷和弯曲是成比例的;从螺旋弹簧的尺寸求弹簧的定数压缩螺旋弹簧的素线径因扭转而产生弯曲的弹簧定数K螺旋弹簧的扭转应力螺旋弹簧的扭转修正应力螺旋弹簧试验载荷下高度端面磨削的情况下螺旋弹簧两端的各厚度之和不同材质螺旋弹簧在高温时的机械特性表3. 不同温度下弹簧的横弹性定数N/mm2表4. 不同温度下弹簧的容许应力N/mm2组合弹簧的计算公式螺旋弹簧的直列和并列弹簧在设计的时候,虽然应该尽可能设计一根弹簧,但是一根弹簧无法满足的情况下,也会对多根弹簧进行组合以满足设计要求;弹簧的组合有纵向排列的直列法和横向排列的并列法两种模式;这样的分类,不仅和螺旋弹簧有关,盘形弹簧等其他种类的弹簧也是一样,也会进行直列和并列组合来使用;从负荷的观点来考虑的话,对各个弹簧作用相等的力的组合方式叫直列,各个弹簧变位相等的组合方式叫并列;图1. 螺旋弹簧的直列组合和并列组合图示显示的是使用了3个弹簧的情况;n个弹簧的各个定数就是k1 , k2 ,, kn弹簧并列和直列组合时全部的定数K公式参照下列;式1. 并列的弹簧定数计算公式式2. 直列的弹簧定数计算公式并列组合的螺旋弹簧的个数增加会导致全体弹簧定数变大,直列组合个数的增加会导致弹簧定数变小;図2. 亲子弹簧并列的字面意思就是横向排列,但是单纯的排列空间上不好安排,所以像图3那样弹簧的内侧和弹簧组合,同心相排的情况下很多;这样的排列一般被称作亲子弹簧;但是,同心组合的情况下,为了弹簧不互相缠绕在一起,交替的改变弹簧卷的方向,或者确保弹簧和弹簧之间有一定的间隙是很有必要的;另外,对弹簧的组合进行下功夫的话,像下图a,b那样,可以制作出不是直线的弹簧特性;例如需要像图4那样特性弹簧的时候,需要对自由长或者不同密着负荷的弹簧进行组合;图5的弹簧特性是在图6那样结构中加入弹簧,事先加上负荷,就会得到〔上段弹簧定数〕<〔下段弹簧定数〕这样的组合;図5.得到特殊弹簧特性的结构弹性能量的计算公式弹簧内积蓄的能量弹簧加上负荷的话,弹簧内就会被积蓄能量;弹簧内积蓄的能量U,和图6中荷重P―変位δ曲线围成的面积相同図6. 弹簧内积蓄的能量用公式3来表示;一般常见的弹簧积蓄能量的公式;公式4适用场合为像上图a那样存在线性关系的时候,也就是公式5另外,说到能量的积蓄和释放,一般会像图6的a,b,c所表示的那样, 增加负荷的时候和去除负荷的时候,是相同的负荷-变位曲线,增加负荷积蓄能量,一旦去除负荷能量就会完全释放,但是像图6d那样具有滞后循环特性的弹簧,被曲线围起来的面积的能量,从增加负荷到去除负荷就会消耗一个周期;螺旋弹簧的振动计算公式螺旋弹簧有固有的振动数弹簧加上负荷,使其变形,加上力,去除力的时候弹簧会发生振动,这个振动数会因不同的弹簧而不同,但是每种弹簧都有其固有的振动数;弹簧自身的质量为m的时候,其固有振动数f就为式6来表示;这里的α ,根据弹簧的固定条件和振动的方向为一定的定数;另外,像图7,8,9,10所表示的那样质量为ms 的弹簧用质量为m 的物体来固定,物体振动时候的固有振动数f0就为 公式7来表示;这里也结合了板簧来进行说明螺旋弹簧-质量系单侧板簧-质量系两端销支撑板簧-质量系两端固定支撑板簧-质量系弹簧的质量ms和物体的质量m相比,一般情况下都比较小,所以一般β看作β=0的情况比较多, 但是必须考虑到弹簧质量的时候,近似图9中β=,图10中β=来进行计算;进行弹簧设计的时候,虽然弹簧的定数很重要,但是这个固有振动数也是必须要考虑到的;弹簧碰撞的计算公式弹簧是为了缓和冲击力碰撞时为了冲击力降低,比较有效果的手段就是使用弹簧;为了评价缓和冲击的能力,像下面那样用缓冲效率η来定义;公式8这里的M为碰撞侧的质量、v0 为碰撞时的速度、Pmax为最大冲击力、δmax为被碰撞侧的最变位; η的值一般为0以上1以下,虽然理想的情况下为1,一定弹簧定数弹簧的碰撞效率η就会变为1/2;1-1 长方形断面的单侧支撑弹簧薄板弹簧最简单的就是长方形断面的单侧支撑弹簧,A为固定端,B为自由端,在B点加上负荷P的情况下的计算公式为这里的I表示2次力矩;来表示,较大的情况下来表示;因此, 较大情况的计算公式为;ν为泊松比、钢的情况下、ν≒;应力在固定端为最大时来表示;这里薄板弹簧材料的纵弹性系数E的值在表2表示;表1. 计算用记号及单位表2.纵弹性系数:EN/m㎡1-2 梯形单侧支撑薄板弹簧计算公式図2像图2那样,薄板弹簧的板厚一定的时候,板幅为直线式变化的情况下,自由端的弯曲为公式4公式中B的计算,根据板厚不同分为下列2种板厚较厚的情况下板厚非常薄厚的情况下、另外,公式中的值,根据β=b1/b可以从图3中求出;图31-3板幅带台阶的薄板弹簧计算公式图4像图4那样,当板厚一定时,板幅带台阶的薄板弹簧的自由端弯曲为,公式5这里,是由P而产生的台阶部位A的弯曲和弯曲角,的长度为,表示板幅的单边弹性的自由端的弯曲;1-4圆环状单侧支撑的薄板弹簧计算公式图5像图5这样,板厚的中心为直线,板幅的中心线为圆弧状,垂直负荷P在自由端作用的时候,任意位置φ的弯曲δφ为这里的C表示板的扭转强度;1-5圆弧状单侧支撑的薄板弹簧计算公式图6板厚的中心线为圆弧状的单侧支撑弹簧,求其在负荷作用下的弯曲,一般利用卡氏定律来求解;以下就是利用该定律的计算结果;如图6表示在圆弧状薄板上,垂直负荷P,水平负荷W各自在中心角的位置上作用的时候,中心角的位置Y方向的弯曲为,X方向的弯曲为;因P产生的弯曲,的时候、公式7的时候、公式8因W产生的弯曲的时候、公式9的时候、公式10图7图7中, 、各自公式如下;公式11公式12图8如图8 的时候,公式13公式14因P产生的最大应力已经在固定端发生,公式15因W产生的最大应力,的时候再图8的A点产生, 的时候在固定端产生,公式161-6 圆轮状的薄板弹簧计算公式图9像图9那样圆轮状的弹簧,因为是上下对称,它的弯曲就是图8的2倍;公式171-7 半圆和1/4圆组合成的薄板弹簧的计算公式图10图10的弯曲为公式18最大应力在固定端产生,公式191-8 圆弧的薄板弹簧的计算公式图11图11左侧所显示的形状自由端的弯曲为公式20如图11右侧形状所示,水平方向被约束的圆弧的弯曲为公式21这两种情况,无论是哪一种,最大应力都为公式221-9 圆弧和带有直线部分的薄板弹簧的计算公式1-9-1其1图12如图12,由直线部分AB和圆弧部分BD组合而成,一端D被固定,另一端A在垂直负荷P或者水平负荷W的作用下,,如以下表示;公式23公式24的时候,公式25W作用的时候,公式26公式27这里,公式中的,为另外,最大应力的时候在固定端产生, 的时候在C点产生;1-9-2 圆弧和带有直线部分的薄板弹簧的计算公式其2图13图13中的弹簧,为2个图12中的弹簧组合在一起,在负荷作用下的弯曲为公式23中得到的倍;公式28图14如图14所示,直线部分和带有圆弧部分弹簧在A端的弯曲为公式29这里、、;最大弯曲应力,在C点产生公式30、的时候,最大应力在固定端发生,,的时候,公式311-9-3 圆弧和带有直线部分的薄板弹簧的计算公式其3图15如图5的情况时,分割AC部分和CD部分,对公式25弯曲的2倍和以下公式的弯曲进行各自的计算,然后结合之后算出A部分的弯曲;公式321-9-4 圆弧和带有直线部分的薄板弹簧的计算公式其4图16如图16所示,直线部分被固定,圆弧部分的A端受到负荷的作用,A端的垂直弯曲和水平弯曲,,受到负荷P作用的时候,公式33公式34受到负荷W作用的时候,公式35公式36图17如图17的形状,受到负荷P作用的时候,公式37公式38受到负荷W作用的时候,公式39公式40这里, ;1-9-5 圆弧和带有直线部分的薄板弹簧的计算公式其5图18如图18所示,曲率半径比较小的圆弧和直线的组合而成的弹簧,忽视圆弧部分的半径之后的弯曲如下所示;公式41最大应力,的时候,在BC部分产生公式42的时候,在固定端产生,公式431-9-6 圆弧和直线部分结合的比较复杂的薄板弹簧的计算公式薄板弹簧的形状,实际上圆弧部分和直线部分复杂结合的情况比较多,可以利用以上介绍的各种公式;以下展示的形状和计算公式都是利用以上所介绍的内容而进行的实际应用;图19图19的形状为2 个图13的组合,可以利用公式28的2倍来求其弯曲;图20图20的形状,两端部分和图10是相同的,应力的公式可以利用公式19来计算;对称轴单侧的弯曲就是公式18加上部分,因此单侧的弯曲就是公式44公式452.特性不同用途的薄板弹簧计算公式2-1 非线性特征的薄板弹簧的计算公式图21非线形特性的薄板弹簧,像图21那样,公式如下显示;式462-2 受到轴负荷和横负荷的薄板弹簧计算公式図22薄板弹簧像图22那样的负荷一般是用来测定机器的;一端被固定,另一端虽然可以横方向运动但是不能旋转;这种情况时,轴负荷P和压弯负荷相比较小,横负荷Q的弯曲及应力为以下公式表示;公式47公式48P比座面负荷大的时候,根据上面公式中的来决定系数以及;这里为,这里的系数,为以下公式;公式49公式502-3 弯曲较大的薄板弹簧的计算公式2-3-1 长方形断面的薄板弹簧图23弯曲较大的情况下,变化到,加上其他影响的计算结果如图24所示;图24图的横轴由表示,纵轴由,表示,表示板的弯曲刚度,比较大的话, ;看图24就可以明白,的值较小的话,也就是负荷P较小的时候,和与1比较相近,的时候,,;因此,这种程度的变形,实际运用中也许并不被采用;2-3-2 梯形单侧支撑薄板弹簧图25图26梯形单侧支撑薄板弹簧的弯曲较大的时候近似值如图25,26所示;横轴为,以为参数,纵轴展示的是弯曲和应力的减少率,这个适用于公式;记号的含义弹簧的设计用记号如下记表1所示,横弹性系数G的值如表2所示;表1. 计算用记号及单位表2.横弹性系数:GN/m㎡线圈部分的弯曲及应力线圈部分弯曲的基本公式是利用压缩弹簧的公式来进行计算的;但是,对于负荷,要考虑到初张力,这个初张力为Pi,任意负荷为P根据公式1,弯曲δ就为另外,剪切应力τ0τ 和压缩弹簧相同,公式如上;钩子部分的应力钩子部分,根据弯曲力矩和扭转力矩会发生拉伸应力以及剪断应力,正确的计算是非常复杂的;这里就对半圆钩子,U 型钩子进行简单的近似计算;i半圆钩子的时候图1中,拉伸应力的最大值在A部分的内侧,剪切应力的最大值在B部分的内侧发生;A部分内侧的最大拉伸应力是弯曲力矩M和轴负荷P的拉伸应力的和,这里的K1是基于曲率的应力集中系数, 代入下列公式;整理公式7,得到但是K1为这里,C为线圈部分的弹簧指数;B部分内侧的最大剪断应力和扭转力矩M相关,得到这里的K2是基于曲率的应力集中系数, 代入下列公式;iiU型钩子的时候图2中,拉伸应力的最大值在A部内侧,剪切应力的最大值在B部的内侧发生;A部分内侧的最大拉伸应力是弯曲力矩M和轴负荷P的拉伸应力的和,公式为这里K3是基于曲率的应力集中系数, 代入下列公式;整理公式13,得到但是K′3 为B部分的最大剪切应力,和半圆钩子相同代入公式11;另外,其他形状的钩子也是同样的考虑方法;。

螺旋箍筋长度计算公式
螺旋箍筋(也称为螺旋弹簧)是一种简单而有效的装置,它可以用来拉紧或松开材料,以实现夹紧、支撑或调整的功能。
螺旋箍筋的长度是其结构的重要参数,因此,计算螺旋箍筋长度是一项重要的任务。
一般来说,计算螺旋箍筋长度的公式如下:
L = 2πr(1 + n)
其中,L表示螺旋箍筋的长度;r表示螺旋箍筋的外径;n表示螺旋箍筋的转数。
首先,在计算螺旋箍筋长度之前,需要确定螺旋箍筋的外径和转数。
一般情况下,螺旋箍筋的外径应该等于它所固定的附件的外径,而转数可以根据实际使用情况来确定。
然后,根据上述公式,只需将实际的外径和转数代入公式,即可求得螺旋箍筋的长度。
例如,如果螺旋箍筋的外径为20mm,转数为3,则螺旋箍筋的长度为2π*20*(1+3)=125.66mm。
最后,在实际使用螺旋箍筋时,应根据要求提供正确的长度,以确保螺旋箍筋的可靠性和使用寿命。
总之,螺旋箍筋的长度可以通过上述公式计算得出,其中,螺旋箍
筋的外径和转数是必不可少的参数。
因此,在计算螺旋箍筋长度时,应根据实际情况确定外径和转数,并根据公式进行计算,以确保螺旋箍筋的使用性能。
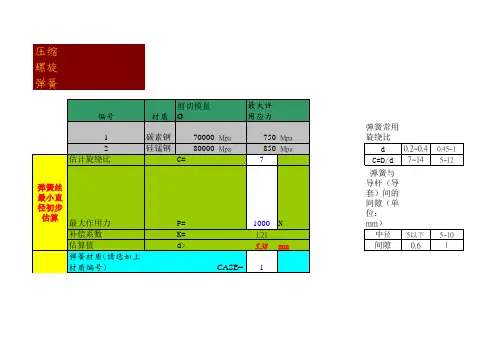
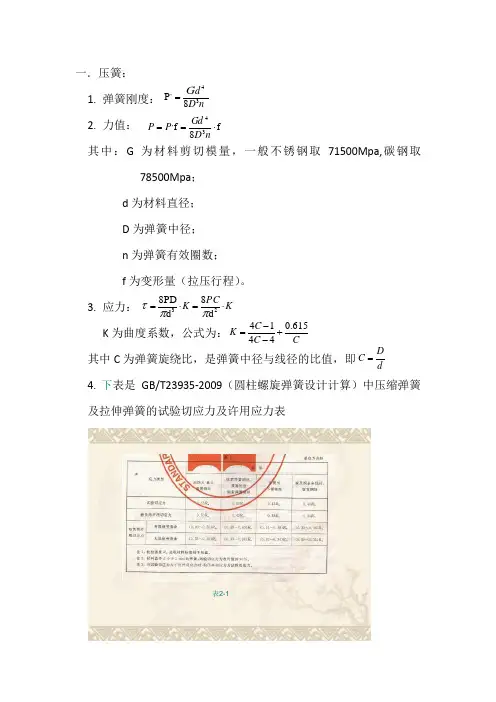
1. 弹簧刚度:
2. 力值: 其中:G 为材料剪切模量,一般不锈钢取71500Mpa,碳钢取
78500Mpa ;
d 为材料直径;
D 为弹簧中径;
n 为弹簧有效圈数;
f 为变形量(拉压行程)。
3. 应力: K 为曲度系数,公式为: 其中C 为弹簧旋绕比,是弹簧中径与线径的比值,即
4. 下表是GB/T23935-2009(圆柱螺旋弹簧设计计算)中压缩弹簧及拉伸弹簧的试验切应力及许用应力表
表2-1
n D d G 34
,
8P =f 8f 34,
⋅==n D Gd P P K PC K ⋅=⋅=2
3d 8d 8PD ππτC
C C K 615.04414+--=d D
C =
比压簧多了初拉力,加上初拉力就行。
初拉力: 其中初拉力τ0按初切应力图选取,见下图。
三.扭簧:
1.计算刚度 Dn
Ed M 3670'4= Nmm/° 2.扭矩 ϕ⋅=Dn
Ed M 36704
Nmm 式中:d---材料直径;
E---材料的弹性模量,一般不锈钢丝取188000Mpa ,碳素钢丝
取206000Mpa ;
D---弹簧外径;
ϕ---弹簧的扭转行程(角度);
4. 应力: K1为曲度系数,顺旋向扭转取1,逆旋向扭转时按下式:
308τπ⋅=D d P 132
.10K d
M ⋅=σ
下表是GB/T23935-2009(圆柱螺旋弹簧设计计算)中扭转弹簧的试验切应力及许用应力表
C
C C C K 4414221---=。

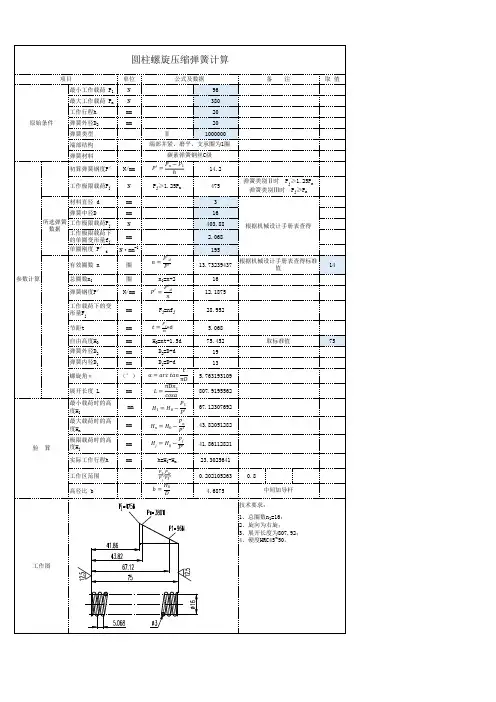
弹簧参数、尺寸及计算公式弹簧参数及尺寸一、小型圆柱螺旋拉伸弹簧尺寸及参数1、弹簧的工作图及形式1.1 工作图样的绘制按GB4459、4规定。
1.2 弹簧的形式分为A型和B型两种。
2、材料弹簧材料直径为0.16~0.45mm,并规定使用GB4357中B组钢丝或YB(T)11中B组钢丝。
采用YB(T)11中B组钢丝时,需在标记中注明代号“S”。
3、制造精度弹簧的刚度、外径、自由长度按GB1973规定的3级精度制造。
如需按2级精度制造时,加注符号“2”,但钩环开口尺寸均按3级精度制造。
4、旋向弹簧的旋向规定为右旋。
如需左旋应在标记中注明“左”。
5、钩环开口弹簧钩环开口宽度a为0.25D~0.35D。
注:D为弹簧中径。
6、表面处理6.1采用碳素弹簧钢丝制造的弹簧,表面一般进行氧化处理,但也可进行镀锌、镀镉、磷化等金属镀层及化学处理。
其标记方法应按GB1238的规定。
6.2采用弹簧用不锈钢丝制造的弹簧,必要时可对表面进行清洗处理,不加任何标记。
7、标记7.1标记的组成弹簧的标记由名称、型式、尺寸、标准编号、材料代号(材料为弹簧用不锈钢丝时)以及表面处理组成。
规定如下:7.2标记示例例1:A型弹簧,材料直径0.20mm,弹簧中径3.20mm,自由长度8.80mm,左旋,刚度、外径和自由长度的精度为2级,材料为碳素弹簧钢丝B组,表面镀锌处理。
标记:拉簧A0.20*3.20*8.80-2左GB1973.2——89-D-Zn例2:B型弹簧,材料直径0.40mm,弹簧中径5.00mm,自由长度17.50mm,右旋,刚度、外径和自由长度的精度为3级,材料为弹簧用不锈钢丝B组。
标记:拉簧B0.40*5.00*17.50 GB1973.2--89-S8、计算依据标准中的计算采用如下基本公式:切应力(N/mm²):τ=(8PDK)/(πd³)变形量(mm):F=(8PD³n)/ Gd4弹簧钢度(N/mm):P′=P/ F=(Gd4)/(8D³n)曲度系数:K =(4C-1)/(4C-4)+ (0.615)/C旋转比:C =D/d 自由长度(mm):H。
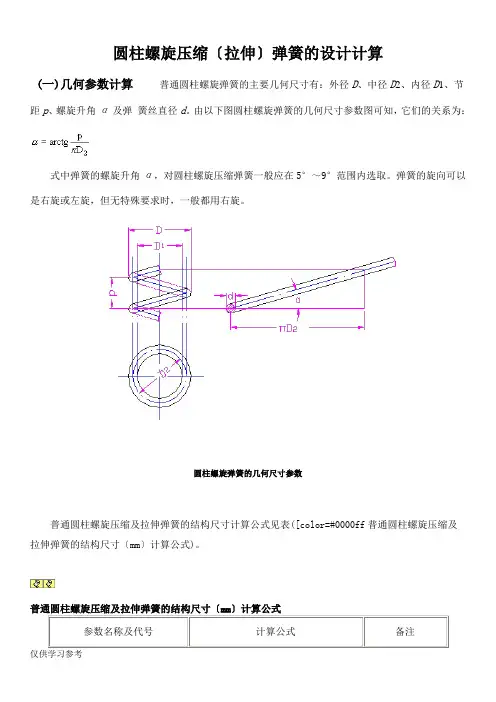
圆柱螺旋压缩〔拉伸〕弹簧的设计计算(一)几何参数计算普通圆柱螺旋弹簧的主要几何尺寸有:外径D、中径D2、内径D1、节距p、螺旋升角α及弹簧丝直径d。
由以下图圆柱螺旋弹簧的几何尺寸参数图可知,它们的关系为:式中弹簧的螺旋升角α,对圆柱螺旋压缩弹簧一般应在5°~9°范围内选取。
弹簧的旋向可以是右旋或左旋,但无特殊要求时,一般都用右旋。
圆柱螺旋弹簧的几何尺寸参数普通圆柱螺旋压缩及拉伸弹簧的结构尺寸计算公式见表([color=#0000ff普通圆柱螺旋压缩及拉伸弹簧的结构尺寸〔mm〕计算公式)。
参数名称及代号计算公式备注工作高度或长度H1,H2,…,H nH n=H0-λn H n=H0+λnλn--工作变形量有效圈数n根据要求变形量按式〔16-11〕计算n≥2总圈数n1n1=n+(2~2.5)〔冷卷〕n1=n+(1.5~2)〔YII型热卷〕n1=n拉伸弹簧n1尾数为1/4,1/2,3/4整圈。
推荐用1/2圈节距p p=(0.28~0.5)D2p=d轴向间距δδ=p-d展开长度L L=πD2n1/cosαL≈πD2n+钩环展开长度螺旋角αα=arct g(p/πD2) 对压缩螺旋弹簧,推荐α=5°~9°质量m sm s=γ为材料的密度,对各种钢,γ=7700kg/;对铍青•(二)特性曲线弹簧应具有经久不变的弹性,且不允许产生永久变形。
因此在设计弹簧时,务必使其工作应力在弹性极限范围内。
在这个范围内工作的压缩弹簧,当承受轴向载荷P时,弹簧将产生相应的弹性变形,如右图a所示。
为了表示弹簧的载荷与变形的关系,取纵坐标表示弹簧承受的载荷,横坐标表示弹簧的变形,通常载荷和变形成直线关系(右图b)。
这种表示载荷与变形的关系的曲线称为弹簧的特性曲线。
对拉伸弹簧,如图<圆柱螺旋拉伸弹簧的特性曲线>所示,图b为无预应力的拉伸弹簧的特性曲线;图c为有预应力的拉伸弹簧的特性曲线。
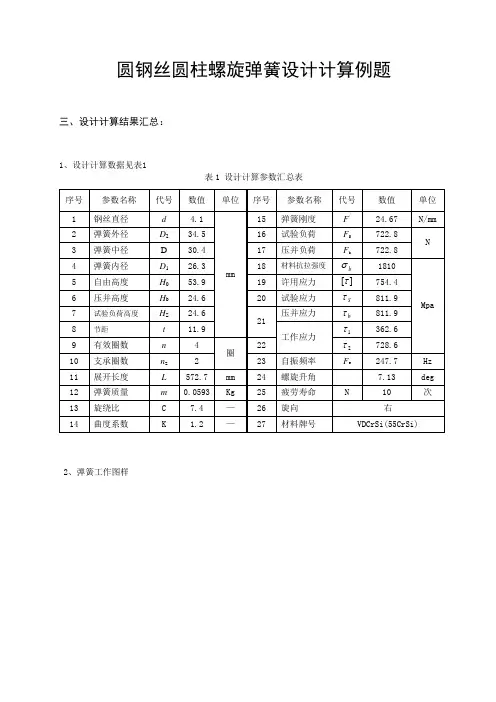
圆钢丝圆柱螺旋弹簧设计计算例题三、设计计算结果汇总:1、设计计算数据见表1表1 设计计算参数汇总表2、弹簧工作图样图1弹簧工作图技术要求a.弹簧端部形式:YI冷卷压缩弹簧;b.总圈数:n1 = 6.0圈;c.有效圈数:n = 4.0圈;d.旋向:右旋;e.强化处理:喷丸和立定处理;f.喷丸强度0.3 A ~ 0.45A,表面覆盖率大于90%;g.表面处理:清洗上防锈油;h.制造技术条件:其余按GB/T 1239.2二级精度。
2) 圆钢丝圆柱螺旋拉伸弹簧设计计算例题例2 :设计一拉伸弹簧,循环次数N =1.0×105次。
工作负荷F =160N,工作负荷下变形量为22mm,采用LⅢ圆钩环,外径D2=21mm。
一、题解分析:a)此拉伸弹簧要求循环次数N = 1.0×107次,由此说明弹簧是按有限寿命设计;b)题设给出了最大工作负荷及对应变形量:c)端部结构采用LⅢ圆钩环,即为圆勾环扭中心;d)弹簧外径D2 = 21mm。
二、解题方法:由以上分析可知,本题中未给出自由高度,说明自由高度可在满足其它条件下按实际计算而定,显然,本题是按表1中第一个设计计算条件及要求给出的。
方法1:严格设计法1)材料选取,根据弹簧使用的疲劳寿命要求,我们可选重要用途的碳素弹簧钢丝E 组别的钢丝,根据弹簧手册P345表10-16查得材料抗拉强度d b ln 3582072-=σ即本讲公式(2)中的 a = 2072;b = -358 从分析可知本弹簧按有限寿命使用,即由表3查得试验切应力的强度系 数为0.5×0.8 = 0.40即:b S στ4.0=;许用切应力系数36.08.045.0=⨯=κ即:b κστ=][ 2) 把题中给定的D = 21mm;F = 160N 及以上所选取的材料所查找的有关强度许用应力系数a = 2072;b = -358; 及36.0=κ代入本讲公式(2):0)2)(ln ()08.054.64(2322222≤-+-+-d d D d b a d d D D F πκ化简得:05644808.439486.25)ln 35.849897.49185()ln 37.80938.4684(234≤+-+---d d d d d d解得:d >2.43 mm 取:d = 2.5mm ;此时,材料抗拉强度)5.2ln(3582072-=b σ=1744Mpa 而查标准附录7—表7.1得b σ= 1680Mpa ; 由此可见相对误差不到3.9%完全满足GB/5311标准的范围,因为标准给出的值按最低值给出。
各种类型弹簧有效圈数的详细计算方法各种类型弹簧有效圈数的详细计算方法:有效圈数是指弹簧能保持相同节距的圈数。
弹簧有效圈数=总圈数-支撑圈,具体根据结构进行计算。
1、对于拉伸弹簧,有效圈数n=总圈数n1,当n;20时圆整为整数圈,当n20时圆整为半圈。
2、对于压缩弹簧,有效圈数n=总圈数n1-支撑圈数n2,n2可查表获得。
尾数应为1/4、1/2、3/4、或整圈。
我们的通俗算法是压簧总圈数减掉上下接受接触不会产生变形的圈数,一般减2圈;扭簧和拉簧的有效圈数就是总圈数。
拓展资料弹簧是一种利用弹性来工作的机械零件。
用弹性材料制成的零件在外力作用下发生形变,除去外力后又恢复原状。
亦作“弹簧”。
一般用弹簧钢制成。
弹簧的种类复杂多样,按形状分,主要有螺旋弹簧、涡卷弹簧、板弹簧、异型弹簧等。
注意问题由于受产品结构限制,多股簧一般具有强度高、性能好的特点。
要求其材料在弹簧强度和韧性上对最终性能予以保证。
多股簧在加工过程中,应注意的是:1、支承圈根据产品要求可选用冷并和热并两种方法。
采用热并方式不允许将簧加热至打火花或发白,硅锰钢温度不得高于850℃。
支承圈与有效圈应有效接触,间隙不得超过圈间公称间隙的10%2、多股簧特性可由调整导程决定,绕制时索距可进行必要调整。
拧距可取3~14倍钢丝直径,但一般取8~13倍为佳。
其簧力还与自由高度、并端圈、外径及钢丝性能等有密切关系,可通过调整其中某项或几项予以改变。
3、不带支承圈的弹簧和钢丝直径过细的弹簧不应焊接簧头,但端头钢索不应有明显的松散,应去毛刺。
凡需焊接头部的多股簧,其焊接部位长度应小于3倍索径(最长不大于10毫米)。
加热长度应小于一圈,焊后应打磨平滑,气焊时焊接部位应进行局部低温退火。
4、弹簧表面处理一般进行磷化处理即可,也可进行其它处理。
凡要进行镀层为锌与镉时,电镀后应进行除氢处理,除氢后抽3%(不少于3件)复试立定处理,复试中不得有断裂。
弹簧应清除表面脏物、盐痕、氧化皮,方法可采用吹砂或汽油清洗的办法,但不能采用酸洗。
圆柱螺旋压缩(拉伸)弹簧的设计计算首先,我们需要确定圆柱螺旋压缩弹簧的几何参数,包括弹簧线径d、弹簧直径D、弹簧长度L以及螺旋数n等。
这些参数决定了弹簧的刚度和
载荷能力。
接下来,我们需要确定弹簧的材料,并获取弹簧材料的力学性
能参数,如弹性模量E、屈服强度σy以及拉伸强度σt等。
在设计计算中,我们首先需要根据工作要求来确定所需的刚度系数k,即弹簧在受到单位长度变形时的力。
刚度系数k可以通过以下公式得到:k=(Gd^4)/(8nD^3)
其中,G为材料的剪切模量。
接下来,我们需要根据弹簧的刚度系数k和工作要求来确定所需的弹
簧力F。
弹簧力F可以通过以下公式计算得到:
F=kL
然后,我们可以根据所需的弹簧力F和弹簧材料的屈服强度σy来确
定所需的弹簧线径d。
弹簧线径d可以通过以下公式计算得到:d=((4F)/(πσy))^(1/2)
接下来,我们需要根据弹簧线径d和螺旋数n来确定所需的弹簧直径D。
弹簧直径D可以通过以下公式计算得到:
最后,我们可以根据所需的弹簧长度L和螺旋数n来确定弹簧的有效
圈数N。
弹簧的有效圈数N可以通过以下公式计算得到:
N=L/(πD)
以上是一种常见的圆柱螺旋压缩弹簧的设计计算方法。
不同的工作要求和应用场景可能需要考虑更多的因素,如弹簧的材料疲劳寿命、弹簧的自振频率等。
因此,在实际设计中,需要根据具体情况进行进一步的计算和分析。
无色为输入值潜蓝色为输出值,自动生成项目输入值名称值材料线径mm d1.4弹簧内径mm D1 5.5弹簧外径mm D 28.3弹簧中径mm D 6.900D=D 1+d 材料弹性模量N/mm² E 206000旋绕比 C 4.93C=D/d材料抗拉强度(应力)MPa σb 1850自由角度 º 270有效圈数 n4.75扭转刚度(N.mm/ º) M'5.651最小负荷扭角º 16最小扭矩N.mm M 190.4最大负荷扭角º76最大扭矩N.mm M 2429.5扭臂1长度 mm L 135.7最小弯曲应力MPa σmin 335.8扭壁2长度 mm L 215最大弯曲应力MPa σmax 1595.1循环特征 γ0.21上限应力系数 σmax/σb 0.86σmax/σb最大负载状态下直径减少量 mm ΔD 0.31导杆直径 mm D'4.67a)、长扭臂弹簧二、疲劳度判断b)、短扭臂弹簧(L 1,L 2=0)公式判定说明:查下表疲劳度图,若γ与σmax/σb值的交点在图中 下方,说明该弹簧的疲劳强度N > 次,σmax/σb=0.7是弹簧不发生永久变形的极限值圆柱螺旋扭转弹簧疲劳度计算一、弹簧参数计算输入参数区域输出区域]}3/)([*3670/{'214L L Dn Ed M ++=ππ1φ2φ)/(3231min d M πσ=)/(3232max d M πσ=max min /σσγ=n10)360/(2n D D φ=∆)(9.0'1D D D ∆-=11'*φM M =22'*φM M =φ)]int([360n n -=φn 10。
无色为输入值潜蓝色为输出值,自动生成项目输入值名称值材料线径mm d 1弹簧内径mm D 1 3.4弹簧外径mm D 25.4弹簧中径mm D 4.400D=D 1+d 材料弹性模量N/mm² E 186000旋绕比 C 4.40C=D/d 材料抗拉强度(应力)MPa σb 1850自由角度 º 0有效圈数 n2扭转刚度(N.mm/ º) M' 4.978最小负荷扭角º 3最小扭矩N.mm M 114.9最大负荷扭角º15最大扭矩N.mm M 274.7扭臂1长度 mm L 17最小弯曲应力MPa σmin 152.2扭壁2长度 mm L 26最大弯曲应力MPa σmax 761.0循环特征 γ0.20上限应力系数 σmax/σb 0.41σmax/σb最大负载状态下直径减少量 mm ΔD 0.09导杆直径 mm D'2.98a)、长扭臂弹簧二、疲劳度判断b)、短扭臂弹簧(L 1,L 2=0)公式判定说明:查下表疲劳度图,若γ与σmax/σb值的交点在图中 下方,说明该弹簧的疲劳强度N > 次,σmax/σb=0.7是弹簧不发生永久变形的极限值圆柱螺旋扭转弹簧疲劳度计算一、弹簧参数计算输入参数区域输出区域]}3/)([*3670/{'214L L Dn Ed M ++=ππ1φ2φ)/(3231min d M πσ=)/(3232max d M πσ=max min /σσγ=n10)360/(2n D D φ=∆)(9.0'1D D D ∆-=11'*φM M =22'*φM M =φ)]int([360n n -=φn 10。