电子科大激光原理课程设计—谐振腔光束仿真

激光原理与技术课程设计---谐振腔自再现模式特性分析XXX uestc1.课程设计任务与要求LD课程设计任务与要求（1）编程计算图示谐振腔的稳定性与光焦度1/F的关系。

可取R1=¥, R2=¥,l1=250mm, l2=200mm。

（2）计算输出镜M2和透镜上的模式半径与光焦度1/F的关系。

（3）取使谐振腔稳定的F值，计算腔内模式半径与z的关系。

（4）取不同的l1值和R1值，计算谐振腔的稳定性，输出镜M2和透镜上的模式半径与光焦度1/F的关系。

（5）进行光线追迹，计算从M1出发，光线参数为(r0, q0)的光线在腔内往返传播的2.实验原理分析1）光焦度与谐振腔稳定性的关系光学谐振腔的稳定性可以用光线往返一周后的【A B C D 】矩阵来描述，根据谐振腔稳定性条件可以判断，当 <1时为稳定腔，当>1时为非稳腔，当=1时为临界腔。

再用matlab 方法作图就可以画出光焦度D 与谐振腔稳定性的关系 2）光焦度与透镜和输出镜作图原理设腔内五个部分的【A B C D 】矩阵分别为 Tr1 Tl1 TF Tl2 Tr2,透镜和输出镜上的传播矩阵分别为T1=Tl1*Tr1*Tl1*TF*Tl2*Tr2*Tl2*TF 和T2=Tl2*TF*Tl1*Tr1*Tl1*TF*Tl2*Tr2;利用matlab 编程得到传播矩阵T1 T2，根据公式 ，用matlab 方法作图就可以画出光焦度D 与透镜和输出镜上光斑半径的关系。

3）z 与光斑半径作图原理算输出镜M2和透镜上的模式半径与光焦度D只要求得光腰半径w0的大小，就可以求出任意处z 的光斑半径大小，而光腰半径w0的大小可以用上述公式逆用求得，根据某一参考面【A B C D 】矩阵，可以求出该处光z,根据公式 作图就可以得到z 和光斑半径的关系。

w()z w =w()z w =4）光线追迹原理设从R1上射出的光线位置参数为【r ；θ】,则传播到透镜上的位置参数为【r F；θF】则二者存在关系式：【r F；θF】=TF*Tl1*【r ；θ】，在左腔镜中，X=0：l1;Y= r F+X θF 根据X，Y的关系就可以做出光线在左腔镜中的传播轨迹，经过透镜和被R2反射的光线也可以利用相同方法求出，重复上述过程，可以得到从某一范围发出的光线在谐振腔内的轨迹图。

激光原理课程设计姓名：班级：学号：基于matlab的激光谐振腔模拟一、引言：谐振腔是激光器的主要构造之一，使激光通过增益物质，实现光的自激振荡。

在激光器出光的过程中,谐振腔内存在许多扰动因素,如腔镜失调、增益介质不均匀、热效应、腔镜变形等,这些腔内扰动因素都会引起不同程度的腔内像差,带来光束质量的下降和光束能量的降低。

谐振腔的经典理论仅给出了部分简单腔型的模式解析解。

对于激光器的不断发展过程中所涌现的许多新型结构谐振腔通常是没有解析结果的,必须采用各种数值模拟方法进行求解。

因此,本文致力于研究迭代解法（Fox-Li 方法）。

Fox-Li 方法是一种模式数值求解中普遍适用的一种方法,只要取样点足够多,它原则上可以用来计算任何形状开腔的自再现模,并且,还可以计算诸如腔镜的倾斜、镜面的不平整性等因素对腔内模式造成的扰动。

二、原理分析：在激光器工作原理中，谐振腔中的模式分布占据着重要的意义。

研究激光谐振腔内激光模式分布及传播规律的经典方法是，运用菲涅耳—基尔霍夫衍射积分公式，其关系式如式（1）：u(x，y)=ik4π∬u（x´，y´）e−ikρρ(1+cosθ)SdS´(1)上式中，ρ为(x’,y’)与(x , y)连线的长度；θ为S面上点(x’,y’)处法线和上述连线之间的夹角；ds’为S面上的面积元；k为波矢的模。

对于开放式光腔，腔面上稳态场分布的形成可以看成是光在两个腔面间往返传播的结果。

考虑在开腔中往返传播的一列波。

设初始时刻在镜I上有某一个场分布1u，则当波在腔中经第一次渡越而到达镜II时，将在镜II上形成一个新的场分布2u，场2u经第二次渡越后又将在镜I上形成一个新的场分布3u。

每次渡越时，波都将因为衍射损失一部分能量，并引起能量分布变化。

由于衍射主要是发生在镜的边缘附近，因此在传播过程中，镜边缘附近的场将衰落得更快，经多次衍射后所形成的场分布，其边缘振幅往往都很小（与中心处比较），具有这种特征的场分布受衍射的影响也将比较小。

摘要激光器谐振腔内的模式计算是提高激光器输出光束质量和应用自适应光学系统校正腔内像差的前提和基础。

在理论分析的基础上,着重采用数值迭代解法（Fox-Li 方法即福克斯和厉鼎毅迭代法）计算平行平面腔（F-P腔）在初始光场三阶梯分布条件下,自再现模的光场振幅的分布。

用数学软件MATLAB建模编写计算程序，计算结果表明,在经过260 次渡越后,归一化的振幅分布实际上已不再发生变化,则已找到光腔的一个自再现模式或横模分布。

关键词: 数值迭代法；光场振幅分布；MATLAB数值模拟目录1 引言 (1)2 理论分析2.1 原理 (2)2.2平行平面腔迭代法的算法实现 (3)3 MATLAB数值模拟 (5)3.1 程序原代码 (5)3.2 数值模拟结果 (6)3.3结果分析 (7)4 总结 (8)【参考文献】 (9)1 引言谐振腔是激光器的主要构造之一，使激光通过增益物质，实现光的自激振荡。

在激光器出光的过程中,谐振腔内存在许多扰动因素,如腔镜失调、增益介质不均匀、热效应、腔镜变形等,这些腔内扰动因素都会引起不同程度的腔内像差,带来光束质量的下降和光束能量的降低。

目前采用自适应光学系统对腔内像差进行校正,定量得到腔内像差扰动对输出光束模式的影响,通过适当的控制算法对像差波前进行实时地校正,而腔内模式计算是这一过程的前提。

平行平面腔（又称为F —P 腔）它由两块平行平面反射镜组成，在激光发展史上最先被采用。

目前，在中等以上功率的固体激光器和气体激光器中仍常常采用它。

其主要优点是，光束方向性极好、模体积较大、比较容易获得单横模振荡等。

谐振腔的经典理论仅给出了部分简单腔型的模式解析解。

对于平行平面腔以及在激光器的不断发展过程中所涌现的许多新型结构谐振腔通常是没有解析结果的,必须采用各种数值模拟方法进行求解。

所以本文基于平行平面腔，研究初始光场三阶梯分布条件下,自再现模的光场振幅。

由于平行平面腔振荡模所满足的自再现积分方程：v(x,y)=γ'''''),(),,,(ds y x v y x y x K s至今尚得不到精确的解析解，因此本文致力于研究平面腔模的迭代解法（Fox-Li 方法）。

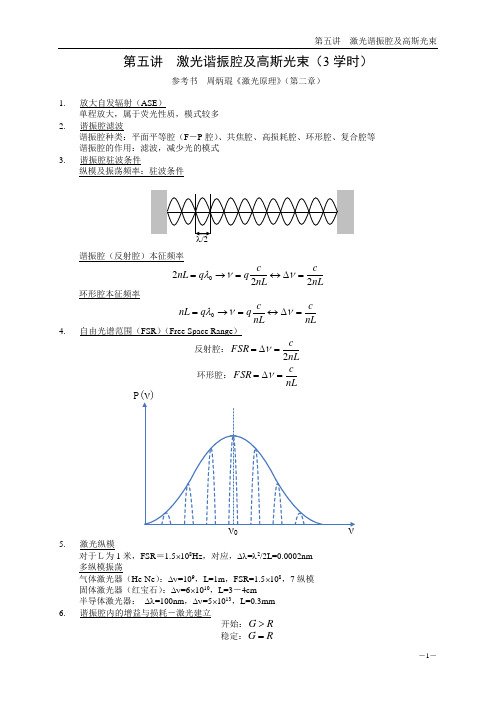
第五讲 激光谐振腔及高斯光束（3学时）参考书 周炳琨《激光原理》（第二章）1. 放大自发辐射（ASE ）单程放大，属于荧光性质，模式较多 2.谐振腔滤波谐振腔种类：平面平等腔（F －P 腔）、共焦腔、高损耗腔、环形腔、复合腔等 谐振腔的作用：滤波，减少光的模式 3.谐振腔驻波条件纵模及振荡频率：驻波条件谐振腔（反射腔）本征频率nL c nL c qq nL 2220=∆↔=→=ννλ 环形腔本征频率nLcnL c qq nL =∆↔=→=ννλ0 4.自由光谱范围（FSR ）（Free Space Range ）反射腔：nL cFSR 2=∆=ν 环形腔：nLcFSR =∆=ν5.激光纵模对于Ｌ为1米，FSR ＝1.5⨯108Hz ，对应，∆λ=λ2/2L=0.0002nm 多纵模振荡气体激光器（He-Ne ）：∆ν=109，L=1m ，FSR=1.5⨯108，7纵模 固体激光器（红宝石）：∆ν=6⨯1010，L=3－4cm半导体激光器： ∆λ=100nm ，∆ν=5⨯1013，L=0.3mm 6.谐振腔内的增益与损耗－激光建立开始：R G > 稳定：R G =7.均匀加宽：单纵模振荡R8. 非均匀加宽：多纵模振荡9.谐振腔内的光场－衍射的自再现 菲涅尔－基尔霍夫衍射积分s d r e y x u iky x u ikrs '+''=-'⎰⎰)cos 1(),(4),(12θπ自再现条件s d y x u L ie y x u y x u y x u s ikr'''==⎰⎰'-),(),(),(1),(12λγγ10. 方形镜腔内光场（直角坐标系下分离变量法）－横模的概念：高斯光束厄米－高斯函数（TEM mn ）πλλπλπ/2222),(L y x n m mn mn e y L H x L H C y x u +-⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=基模高斯函数（TEM 00）)/1( ),(20200/0000022e L eC e C y x u r L y x 功率下降为中心最大的πλωωπλ===⎪⎪⎭⎫ ⎝⎛-+-高阶横模（TEM mn ）11. 圆形镜腔内光场（柱坐标系下分离变量法）拉盖尔－高斯函数ϕωωωim r m n mmn mn e er L r C y x u --⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=22202022),(TEM 00TEM 10TEM01 TEM 01 TEM 11高阶横模（TEM mn ） 12. 基模高斯光束传输－远场发散角光场分布（沿z 方向传输）)(111 1)(12)(12),,(22022)()()(222222z iR q z z R zez eez z y x u z z z q y x iz R y x iz y x πωλλπωπωλωωωπωπλπλπω-=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫⎝⎛+==⋅⋅=+-+-+-/102 22πωλπλθπλω===F F e 腰的传播变粗、腰越大，发散角越小。

《激光原理》课程教学大纲一、课程基本信息二、课程简介本课程是“光电器件加工”课程模块中的专业核心课程，以培养应用能力突出、能适应工作变化和具有创新素质的学生为目标，在教学内容上，将理论教学与案例教学有机地结合进行知识点讲解，注重培养学生运用基础物理知识分析解决激光相关问题的能力；在教学模式上，采用研讨式的教学模式，注重引导学生对激光技术相关领域的核心问题已有的解决方案进行分析比较，培养学生的问题分析能力。

在培养学生熟练掌握激光器结构、工作原理、调Q技术与锁模技术的基础上，提升学生的综合能力和解决复杂问题的能力，为学生成为新一代技术应用型人才奠定基础。

三、课程目标及对毕业要求（及其指标点）的支撑四、教学内容及进度安排五、课程考核六、教材及参考资料(一)课程教材1.《激光原理及应用》（第3版），陈鹤鸣等编著，电子工业出版社，2017(二)参考教材及网站1.《激光原理》（第7版），周炳琨等编著，国防工业出版社，2014。

2.《激光原理及应用》（第3版），陈家璧等编著，电子工业出版社，2013。

3.《激光原理及技术》，电子科技大学，刘志军等主讲，中国大学慕课。

编写人：审核人：审批人：审批日期：附件：各类考核与评价标准表（1）考试方式及占比：采用闭卷笔试，考试成绩100分，占课程考核成绩的60%。

（2）评定依据：考试成绩的评定根据试卷参考答案和评分标准进行。

（3）考试题型：可以包含单项选择题、填空题、简答题、计算题和设计题。

（4）考试内容：对学生综合运用激光物理的基本概念、基本原理进行问题分析能力的考核，不仅包括对各章节知识点的独立考核，还需要包括综合考虑多种激光器性能与控制的改善方案，实现技术分析和解决复杂工程问题能力的考核。

课程设计题目：谐振腔的稳定性分析和自再现高斯光束计算姓名：学号：指导老师：时间：电子科技大学光电信息学院任务一：如图A 所示的谐振腔，用Matlab 程序计算光线在腔内的轨迹，演示腔的稳定和不稳定时光线在腔内往返次数增加时光线轨迹。

初始光线任意选择。

图A 两球面镜组成的谐振腔实现方法：首先利用列阵r θ⎡⎤⎢⎥⎣⎦描述任光线的坐标，而用传输矩阵i i i i i A B T C D ⎡⎤=⎢⎥⎣⎦描述光线经过一段空间后所引起的坐标变换。

假设光线在腔内经n 次往返时其参数的变换关系以矩阵的形式表示：n n r θ⎡⎤⎢⎥⎣⎦=1n i i T =∏11r θ⎡⎤⎢⎥⎣⎦用 计算出光线的路径。

如此循环得到腔内的光线轨迹。

实现程序：见 源程序（1）模拟结果：稳定情况下 非稳定情况下R1=500mm,R2=600mm,L=700mm R1=250mm,R2=300mm,L=700mmL=700mmR1=500m R2=600m任务二：如图所示的谐振腔，由球面放射镜和平面放射镜之间插入一薄透镜构成。

图B 平面镜和凹面镜之间插入薄透镜谐振腔（1） 分析计算透镜与平面镜之间的距离在什么范围内腔是稳定的；（2） 在腔稳定情况下，演示在腔内往返100次以上时光线轨迹；（3） 计算自再现高斯光束的q 参数，并演示往返一周腔内光斑半径曲线自再现（波长为0.5um ）。

实现方法：（1）计算谐振腔的传输矩阵 ，利用公式计算的值，判断当时，谐振腔是稳定的，当不再范围内时，谐振腔是非稳定的。

（2）其实现方法同任务一的方法一样。

（3）计算谐振腔内各个平面上的q 参数，根据，求得和，利用 求得，用 画出光线在谐振腔内往返一周的光斑半径曲线，同时验证谐振腔模式的自再现。

实现程序：见 源程序（2.2）和（2.3）R1=1000m F=50mmL1 L=800mm模拟结果：（1）经计算当R1=1000mm，F=50mm，L=800mm时，L1在40mm至55.333mm时腔稳定。

电子科技大学课程设计激光原理与技术题目:谐振腔的稳定性分析和自在现高斯光束计算姓名: 陈沫学号: 2905301005指导老师: 余学才课程设计：谐振腔的稳定性分析和自在现高斯光束计算一:课程设计题目：如图所示的谐振腔，由球面反射镜和平面反射镜之间插入一薄透镜构成。

（1）分析计算透镜与平面镜之间距离在什么范围内腔是稳定的；（2）在腔稳定情况下，演示在腔内往返100次以上时光线轨迹；（3）计算自再现高斯光束的q参数，并演示往返一周腔内光斑半径曲线自再现（波长）要求: 追踪光线在谐振腔内的轨迹、自再现高斯光束和非自在线高斯光束在腔内的光斑半径。

设计原理：高斯光束的光斑半径w(z)=w01+z2/f2，在z=0处w(z=0)=w0为光束最小光斑半径，称为光腰半径，q参数定义为1q(z)=1R(z)−iλπω2(z)；其中R z=z+f2/z q参数也可写为q(z)=if+z；q参数的实部表示光腰的距离，虚部表示共焦参数。

q参数经过无几何像差的光学系统的变换关系为q0=Aq i+BCq i+D ；A,B,C,D是系统传播矩阵的元素，T=A BC D;谐振模式高斯光束的q参数满足q M=Aq M+BCq M+D ；所以q M=(A−D2i−+1−A+D24)/2C；腔的稳定性判据是−1<A+D2<1。

（一）分析：计算出从第一个凹面镜R开始往返一周的传输矩阵TRR=A BC D；再根据稳定性条件−1<A+D<1求出凸透镜到第二面镜子之间距离l1的范围。

2程序：clearsyms LL;R=1000;F=50;L=800;TL=[1 L;0 1];TM=[1 0;-1/F 1];TR2=[1 0;0 1];TR1=[1 0;-2/R 1];TL1=[0 LL;0 1];TRR=TR1*TL*TM*TL1*TR2*TL1*TM*TL;S=(TRR(1)+TRR(4))/2;X1=solve(S-1);X2=solve(S+1);disp(['距离L在',char(X2),'<L<',char(X1),' 内腔是稳定的'])结果:距离L在100/3<L<60 内腔是稳定的。

一．课程设计的主要任务：1.任务总述：用计算机模拟激光谐振腔的光场分布。

2.设计要求： 1）编程语言不限；2）腔型包括：条形腔，矩形平平腔，圆形平平腔，矩形共焦腔，圆形共焦腔，倾斜腔等。

二．我个人完成的情况：1.已经完成的：1）用基本的循环迭代法：模拟了条形腔，矩形平平腔，圆形平平腔，矩形共焦腔，圆形共焦腔的光场的振幅和相位分布：2）用传输矩阵结合分离变量的方法：模拟了条形腔，矩形平平腔，矩形共焦腔的光场的振幅和相位分布。

三，基本原理：1.一般的迭代法的基本原理：1)基于菲涅尔衍射积分的基本原理：设左右镜面的任意两个点P 和P ’点，光场分别为),(y x u 和)','(y x u ，θ是PP ’连线和光轴的夹角，ρ为PP ’之间的距离，则：⎰⎰+=-Sik dS ey x u iky x u ')cos 1()','(4),(θρπρ同理：因此，左右通过上两式可以把激光谐振腔的左右有效地联系在一起，给出一个面的初始光场分布，经过往返迭代，可以得出如下的光场分布特性： j j y x u y x u ）','(1),(1γ=+ 12,(1)','(++=j j y x u y x u ）γ则说明激光谐振腔达到了自再现的条件，也是镜面上的场分布的稳定性条件。

2）网格化的思想：虽然实际的腔镜面上的光场分布是连续的，但考虑到用计算机计算的离散的特性，需要把腔镜分割成网格，以网格上离散的节点的光场值去拟合实际的镜面的光场。

根据镜面的几何结构的特点，分割方法不尽相同，具如下： A.条形腔：等间距取点，（示意图略）：B,矩形镜面：如下图左所示的方法进行等间隔分割与取点； C,圆形镜面：如下图右所示的方法进行等间距等角度离散。

3）化积分的运算为求和的思想：结果加和存于一个二维数组中，通过循环，完成每一点的求和，具体的见代码（附有详细的注释）。