2019版高考数学一轮复习第8章平面解析几何8.5椭圆课后作业理

第5讲 椭圆板块四 模拟演练·提能增分[A 级 基础达标]1．[2016·湖北八校联考]设F 1，F 2为椭圆x 29＋y 25＝1的两个焦点，点P 在椭圆上，若线段PF 1的中点在y 轴上，则|PF 2||PF 1|的值为( )A.514B.513C.49D.59 答案 B解析 由题意知a ＝3，b ＝5，c ＝2.设线段PF 1的中点为M ，则有OM ∥PF 2，∵OM ⊥F 1F 2，∴PF 2⊥F 1F 2，∴|PF 2|＝b 2a ＝53.又∵|PF 1|＋|PF 2|＝2a ＝6，∴|PF 1|＝2a －|PF 2|＝133，∴|PF 2||PF 1|＝53×313＝513.故选B.2．已知中心在原点的椭圆C 的右焦点为F (1,0)，离心率等于12，则C 的方程是( )A.x 23＋y 24＝1B.x 24＋y 23＝1 C.x 24＋y 22＝1 D.x 24＋y 23＝1 答案 D解析 依题意，所求椭圆的焦点位于x 轴上，且c ＝1，e ＝c a ＝12⇒a ＝2，b 2＝a 2－c 2＝3，因此椭圆C 的方程是x 24＋y 23＝1.3．“－3<m <5”是“方程x 25－m ＋y 2m ＋3＝1表示椭圆”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件答案 B解析 要使方程x 25－m ＋y 2m ＋3＝1表示椭圆，只须满足⎩⎪⎨⎪⎧5－m >0，m ＋3>0，5－m ≠m ＋3，解得－3<m <5且m ≠1，因此，“－3<m <5”是“方程x 25－m ＋y 2m ＋3＝1表示椭圆”的必要不充分条件．故选B.4．已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的一个焦点是圆x 2＋y 2－6x ＋8＝0的圆心，且短轴长为8，则椭圆的左顶点为( )A ．(－3,0)B ．(－4,0)C ．(－10,0)D ．(－5,0)答案 D解析 圆的标准方程为(x －3)2＋y 2＝1，∴圆心坐标是(3,0)，∴c ＝3.又b ＝4，∴a ＝b 2＋c 2＝5.∵椭圆的焦点在x 轴上，∴椭圆的左顶点为(－5,0)．故选D.5．[2018·黑龙江双鸭山模拟]过椭圆x 2a 2＋y 2b2＝1(a >b >0)的两个焦点作垂直于x 轴的直线与椭圆有四个交点，且这四个交点恰好为正方形的四个顶点，则椭圆的离心率为( )A.5＋14 B.5－12 C.3－12 D.3＋14答案 B解析 ∵过椭圆的两个焦点作垂直于x 轴的直线与椭圆有四个交点，且这四个交点恰好为正方形的四个顶点，∴c ＝b 2a ，即ac ＝a 2－c 2，∴e 2＋e －1＝0，∵0<e <1，∴e ＝5－12，故选B.6．[2018·惠来月考]以F 1(－1,0)，F 2(1,0)为焦点且与直线x －y ＋3＝0有公共点的椭圆中，离心率最大的椭圆方程是( )A.x 220＋y 219＝1B.x 29＋y 28＝1C.x 25＋y 24＝1 D.x 23＋y 22＝1 答案 C解析 解法一：由题意知，c ＝1，a 2－b 2＝1，故可设椭圆的方程为x 2b 2＋1＋y 2b2＝1，离心率的平方为：1b 2＋1①， ∵直线x －y ＋3＝0与椭圆有公共点，将直线方程代入椭圆方程得(2b 2＋1)x 2＋6(b 2＋1)x ＋8b 2＋9－b 4＝0，由Δ＝36(b 4＋2b 2＋1)－4(2b 2＋1)(8b 2＋9－b 4)≥0， ∴b 4－3b 2－4≥0，∴b 2≥4，或b 2≤－1(舍去)， ∴b 2的最小值为4，∴①的最大值为15，此时，a 2＝b 2＋1＝5，∴离心率最大的椭圆方程是：x 25＋y 24＝1.故选C.解法二：令直线x －y ＋3＝0与椭圆的一个交点为P ，则2a ＝|PF 1|＋|PF 2|，∵e ＝2c 2a ＝22a ，∴当|PF 1|＋|PF 2|最小时e 最大，F 1，F 2在直线x －y ＋3＝0的同侧，F 1关于x －y ＋3＝0的对称点F 1′(－3,2)，∴|PF 1|＋|PF 2|＝|PF 1′|＋|PF 2|≥|F 1′F 2|＝25，即2a ≥25，a ≥5，当a ＝5时e 最大，此时b 2＝a 2－c 2＝4，所求椭圆方程为x 25＋y 24＝1.故选C.7．[2018·深圳检测]若x 2＋ky 2＝2表示焦点在y 轴上的椭圆，则实数k 的取值范围是________．答案 (0,1)解析 将椭圆的方程化为标准形式得y 22k＋x 22＝1，因为x 2＋ky 2＝2表示焦点在y 轴上的椭圆，所以2k>2，解得0<k <1.8．[2018·江西模拟]过点M (1,1)作斜率为－12的直线与椭圆C ：x 2a 2＋y2b 2＝1(a >b >0)相交于A ，B 两点，若M 是线段AB 的中点，则椭圆C 的离心率等于________．答案22解析 设A (x 1，y 1)，B (x 2，y 2)分别代入椭圆方程相减得x 1－x 2x 1＋x 2a 2＋y 1－y 2y 1＋y 2b2＝0，根据题意有x 1＋x 2＝2×1＝2，y 1＋y 2＝2×1＝2，且y 1－y 2x 1－x 2＝－12，所以2a 2＋2b 2×⎝ ⎛⎭⎪⎫－12＝0，得a 2＝2b 2，所以a 2＝2(a 2－c 2)，整理得a 2＝2c 2，得c a ＝22，所以e＝22. 9．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为e ＝32，其左、右焦点分别为F 1，F 2，|F 1F 2|＝23，设点M (x 1，y 1)，N (x 2，y 2)是椭圆上不同两点，且这两点分别与坐标原点的连线的斜率之积为－14.(1)求椭圆C 的方程；(2)求证：x 21＋x 22为定值，并求该定值． 解 (1)∵c ＝3，e ＝32，∴a ＝2，b 2＝a 2－c 2＝1， 则椭圆C 的方程为x 24＋y 2＝1.(2)证明：由于y 1x 1·y 2x 2＝－14，则x 1x 2＝－4y 1y 2，x 21x 22＝16y 21y 22.而x 214＋y 21＝1，x 224＋y 22＝1，则1－x 214＝y 21，1－x 224＝y 22，∴⎝ ⎛⎭⎪⎫1－x 214⎝ ⎛⎭⎪⎫1－x 224＝y 21y 22，则(4－x 21)(4－x 22)＝16y 21y 22，(4－x 21)(4－x 22)＝x 21x 22，展开得x 21＋x 22＝4为一定值．10．[2018·山东模拟]已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的两个焦点和短轴的两个端点都在圆x 2＋y 2＝1上．(1)求椭圆C 的方程；(2)若斜率为k 的直线过点M (2,0)，且与椭圆C 相交于A ，B 两点，试探讨k 为何值时，OA ⊥OB .解 (1)依题意b ＝1，c ＝1，所以a 2＝2. 所以椭圆C 的方程为x 22＋y 2＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，直线AB 的方程为y ＝k (x －2)．由⎩⎪⎨⎪⎧y ＝k x －2，x 22＋y 2＝1消去y 得(1＋2k 2)x 2－8k 2x ＋8k 2－2＝0.所以x 1＋x 2＝8k 21＋2k 2，x 1x 2＝8k 2－21＋2k 2.因为OA ⊥OB ，所以x 1x 2＋y 1y 2＝0. 而y 1y 2＝k 2(x 1－2)(x 2－2)， 所以x 1x 2＋k 2(x 1－2)(x 2－2)＝0， 即(1＋k 2)x 1x 2－2k 2(x 1＋x 2)＋4k 2＝0， 所以1＋k28k 2－21＋2k2－16k 41＋2k2＋4k 2＝0， 解得k 2＝15，此时Δ>0，所以k ＝±55.[B 级 知能提升]1．[2018·湖南郴州]设e 是椭圆x 24＋y 2k ＝1的离心率，且e ∈⎝ ⎛⎭⎪⎫12，1，则实数k 的取值范围是( )A ．(0,3) B.⎝⎛⎭⎪⎫3，163C ．(0,3)∪⎝ ⎛⎭⎪⎫163，＋∞D ．(0,2)答案 C解析 当k >4时，c ＝k －4，由条件知14<k －4k <1，解得k >163；当0<k <4时，c ＝4－k ，由条件知14<4－k4<1，解得0<k <3，故选C.2．[2018·重庆模拟]已知F 1，F 2为椭圆C ：x 29＋y 28＝1的左、右焦点，点E 是椭圆C 上的动点，EF 1→·EF 2→的最大值、最小值分别为( )A ．9,7B ．8,7C ．9,8D ．17,8 答案 B解析 由题意可知椭圆的左右焦点坐标为F 1(－1,0)，F 2(1，0)，设E (x ，y )，则EF 1→＝(－1－x ，－y )，EF 2→＝(1－x ，－y )，EF 1→·EF 2→＝x 2－1＋y 2＝x 2－1＋8－89x 2＝19x 2＋7(－3≤x ≤3)，所以当x ＝0时，EF 1→·EF 2→有最小值7，当x ＝±3时，EF 1→·EF 2→有最大值8，故选B.3.[2018·鼓楼期末]由半椭圆x 2a 2＋y 2b 2＝1(x ≥0)与半椭圆x 2c 2＋y 2b 2＝1(x ≤0)合成的曲线称作“果圆”，如图所示，其中a 2＝b 2＋c 2，a >b >c >0.由右椭圆x 2a 2＋y 2b2＝1(x ≥0)的焦点F 0和左椭圆x 2c 2＋y 2b 2＝1(x ≤0)的焦点F 1，F 2确定的△F 0F 1F 2叫做果圆的焦点三角形，若果圆的焦点三角形为锐角三角形，则右椭圆x 2a 2＋y 2b2＝1(x ≥0)的离心率的取值范围为( )A.⎝ ⎛⎭⎪⎫13，1 B.⎝⎛⎭⎪⎫23，1 C.⎝⎛⎭⎪⎫33，1 D.⎝⎛⎭⎪⎫0，33 答案 C解析 连接F 0F 1、F 0F 2，根据“果圆”关于x 轴对称，可得△F 1F 0F 2是以F 1F 2为底边的等腰三角形， ∵△F 0F 1F 2是锐角三角形，∴等腰△F 0F 1F 2的顶角为锐角，即∠F 1F 0F 2∈⎝⎛⎭⎪⎫0，π2.由此可得|OF 0|>|OF 1|，∵|OF 0|、|OF 1|分别是椭圆x 2a 2＋y 2b 2＝1、x 2c 2＋y 2b2＝1的半焦距，∴c >b 2－c 2，平方得c 2>b 2－c 2，又∵b 2＝a 2－c 2，∴c 2>a 2－2c 2，解得3c 2>a 2， 两边都除以a 2，得3·⎝ ⎛⎭⎪⎫c a 2>1，解之得c a >33. ∵右椭圆x 2a 2＋y 2b 2＝1(x ≥0)的离心率e ＝ca∈(0,1)，∴所求离心率e 的范围为⎝⎛⎭⎪⎫33，1.故选C. 4．[2017·北京高考]已知椭圆C 的两个顶点分别为A (－2，0)，B (2,0)，焦点在x 轴上，离心率为32. (1)求椭圆C 的方程；(2)点D 为x 轴上一点，过D 作x 轴的垂线交椭圆C 于不同的两点M ，N ，过D 作AM 的垂线交BN 于点E .求证：△BDE 与△BDN 的面积之比为4∶5.解 (1)设椭圆C 的方程为x 2a 2＋y 2b 2＝1(a >b >0)，由题意得⎩⎪⎨⎪⎧a ＝2，c a ＝32，解得c ＝3，所以b 2＝a 2－c 2＝1，所以椭圆C 的方程为x 24＋y 2＝1.(2)证明：设M (m ，n )，则D (m,0)，N (m ，－n )， 由题设知m ≠±2，且n ≠0.直线AM 的斜率k AM ＝nm ＋2，故直线DE 的斜率k DE ＝－m ＋2n， 所以直线DE 的方程为y ＝－m ＋2n(x －m )， 直线BN 的方程为y ＝n2－m(x －2)．联立⎩⎪⎨⎪⎧y ＝－m ＋2n x －m ，y ＝n2－m x －2，解得点E 的纵坐标y E ＝－n 4－m 24－m 2＋n2.由点M 在椭圆C 上，得4－m 2＝4n 2，所以y E ＝－45n .又S △BDE ＝12|BD |·|y E |＝25|BD |·|n |，S △BDN ＝12|BD |·|n |，所以△BDE 与△BDN 的面积之比为4∶5.5．已知过点A (0,2)的直线l 与椭圆C ：x 23＋y 2＝1交于P ，Q 两点．(1)若直线l 的斜率为k ，求k 的取值范围；(2)若以PQ 为直径的圆经过点E (1,0)，求直线l 的方程． 解 (1)依题意，直线l 的方程为y ＝kx ＋2，由⎩⎪⎨⎪⎧x 23＋y 2＝1，y ＝kx ＋2消去y 得(3k 2＋1)x 2＋12kx ＋9＝0，令Δ＝(12k )2－36(3k 2＋1)>0， 解得k >1或k <－1，所以k 的取值范围是(－∞，－1)∪(1，＋∞)． (2)当直线l 的斜率不存在时，直线l 的方程为x ＝0， 则P (0,1)，Q (0，－1)或P (0，－1)，Q (0,1)， 此时以PQ 为直径的圆过点E (1,0)，满足题意． 当直线l 的斜率存在时，设直线l 的方程为y ＝kx ＋2，P (x 1，y 1)，Q (x 2，y 2)，又E (1,0)，所以EP →＝(x 1－1，y 1)，EQ →＝(x 2－1，y 2)． 由(1)知x 1＋x 2＝－12k 3k 2＋1，x 1x 2＝93k 2＋1，所以EP →·EQ →＝(x 1－1)(x 2－1)＋y 1y 2 ＝x 1x 2－(x 1＋x 2)＋1＋(kx 1＋2)(kx 2＋2) ＝(k 2＋1)x 1x 2＋(2k －1)(x 1＋x 2)＋5＝9k 2＋13k 2＋1＋(2k －1)⎝ ⎛⎭⎪⎫－12k 3k 2＋1＋5 ＝12k ＋143k 2＋1. 因为以PQ 为直径的圆过点E (1,0)， 所以EP →·EQ →＝0，即12k ＋143k 2＋1＝0，解得k ＝－76，满足Δ>0，故直线l 的方程为y ＝－76x ＋2，综上，所求直线l 的方程为x ＝0或y ＝－76x ＋2.。

8・5椭E课后作业孕谀［重点保分两级优选练］A级一、选择题2 1・（2018 •江西五市八校模拟）已知正数/〃是2和8的等比中项，则圆锥曲线/+~=1 m的焦点坐标为（）A.（土0）B. （0, 土羽）C. （±萌，0）或仕0）D. （0, 土羽）或仕0）答案B解析因为正数/〃是2和8的等比中项，所以駢=16,则〃尸4,所以圆锥曲线/+-= m2 _1即为椭圆%+f=l,易知其焦点坐标为（0, 土寸5）,故选B.32.（2017 •湖北荆门一模）已知〃是△肋C的一个内角，且sin 〃+cos 0 =-,则方稈/sin 0 —ycos〃 = 1 表示（）A.焦点在x轴上的双曲线B.焦点在y轴上的双曲线C.焦点在％轴上的椭圆D.焦点在y轴上的椭圆答案D9 7解析因为（sin 0 +cos 〃）'=l+2sin 〃cos 0 =77,所以sin 〃cos 0 = —~<0,结合3〃w(0, JI ),知sin 〃>0, cos 〃〈0,又sin 〃+cos 〃 =[>(),所以sin 〃>—cos 0>O,] 1 2 2故---- >—-7>0,因为Ain ^-/cos 0 = \可化为V=1,所以方程— cos u sm u ] ]cos & sin 0xsin 〃一ycos 〃 = 1表示焦点在y轴上的椭圆.故选D.3.（2018 •湖北八校联考）设凡用为椭圆1的两个焦点，点戶在椭圆上，若线\PFA 段〃的中点在y轴上，则=的值为（5A•肓)5B-B5D-9答案B解析 由题意知自=3, b=弟,c=2.设线段〃的中点为必则有如〃/雄，V OMA_F^, ・•・％丄F\F?.,E 5/. I PFi I =一=孑又・・•丨朋丨+丨朋I =2^=6,a o・・・|〃|=2日一|处|=¥，扌X^=鲁，故选B.x y _4. （2017 •全国卷III ）已知椭圆a -+4=l （a>Z7>0）的左、右顶点分别为几 血 且以a b线段畀/2为直径的圆与直线bx-ay+2ab= 0相切，则C 的离心率为（）1 D -3答案A解析 由题意知以昇必2为直径的圆的圆心为（0, 0）,半径为日. 又直线bx — ay+2ab=^与圆相切，•••圆心到直线的距离d=~F==a,y/a + b1 D -I 答案# / X V因为椭圆飞+〒=1 （日〉力>0）与双曲线飞一==1 （刃>0, 〃>0）有相同的焦点（一G 0）和 a bm n （c, 0）,所以 C=a —li=m +因为c 是日，/〃的等比中项，/是2〃,与d 的等差中项，所以c=am, 2n=2m + c ,所以殳 9 c cc 1 c 1 卜刁所以—+y=c,化为7=了所以尸一=孑故选C.Z d Z d T 3 Z6. （2017 •荔湾区期末）某宇宙飞船运行的轨道是以地球屮心为一焦点的椭圆，测得近地 点距地面刃千米，远地点距地面/7千米，地球半径为厂千米，则该飞船运行轨道的短轴长为解得 a=yfib,b 1 訂乔c J 孑 e=——=a ax y 5.已知椭圆~+y?= 1（臼〉方＞0）与双|tt|线厂汗iS>o,讪有相同的焦点（-小和（。

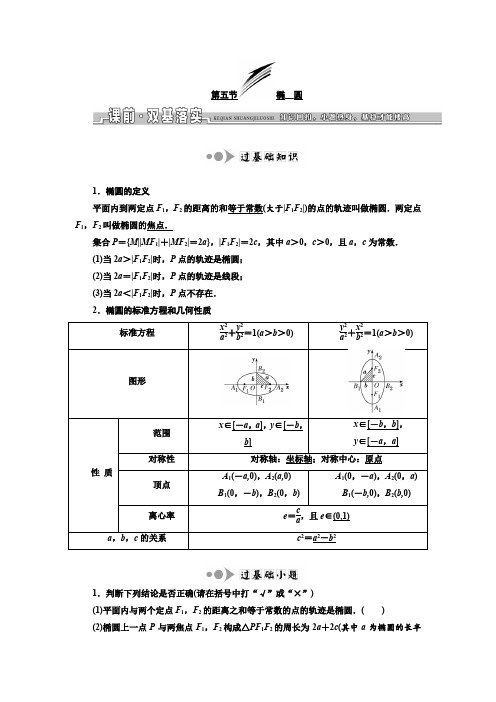
第5讲 椭 圆）1．椭圆的定义 条件 结论1 结论2 平面内的动点M与平面内的两个定点F 1，F 2M 点的 轨迹为 椭圆 F 1、F 2为椭圆的焦点 ｜MF 1|＋|MF 2|＝2a|F 1F 2｜为椭圆的焦距 2a ＞|F 1F 2|2。

椭圆的标准方程和几何性质 标准方程 错误!＋错误!＝1（a ＞b ＞0） 错误!＋错误!＝1（a ＞b ＞0）图形性质 范围－a ≤x ≤a －b ≤y ≤b －b ≤x ≤b －a ≤y ≤a 对称性对称轴：x 轴、y 轴 对称中心:(0，0） 顶点 A 1(－a ，0),A 2（a ，0) B 1(0，－b ），B 2(0，A 1（0,－a ），A 2(0，a )B 1(－b ，0），B 2（b ，b）0）轴长轴A1A2的长为2a 短轴B1B2的长为2b焦距|F1F2|＝2c离心率e＝错误!，e∈（0,1）a,b，c的关系c2＝a 2－b21．辨明两个易误点（1）椭圆的定义中易忽视2a＞|F1F2｜这一条件，当2a＝|F1F2｜时，其轨迹为线段F1F2，当2a＜|F1F2|时,不存在轨迹．(2)求椭圆的标准方程时易忽视判断焦点的位置,而直接设方程为错误!＋错误!＝1(a＞b＞0)．2．求椭圆标准方程的两种方法（1)定义法：根据椭圆的定义，确定a2，b2的值，结合焦点位置可写出椭圆方程．（2）待定系数法：若焦点位置明确，则可设出椭圆的标准方程，结合已知条件求出a、b;若焦点位置不明确，则需要分焦点在x轴上和y轴上两种情况讨论，也可设椭圆的方程为Ax2＋By2＝1(A＞0，B ＞0,A≠B）．1.错误!椭圆C：错误!＋错误!＝1的左右焦点分别为F1，F2，过F2的直线交椭圆C于A、B两点,则△F1AB的周长为（）A．12 B．16C．20 D．24C △F1AB的周长为|F1A｜＋|F1B|＋｜AB|＝|F1A｜＋｜F2A|＋|F1B|＋｜F2B|＝2a＋2a＝4a。

8．5 椭圆[重点保分 两级优选练]A 级一、选择题1．(2018·江西五市八校模拟)已知正数m 是2和8的等比中项，则圆锥曲线x 2＋y 2m＝1的焦点坐标为( )A ．(±3，0)B ．(0，±3)C ．(±3，0)或(±5，0)D ．(0，±3)或(±5，0)答案 B解析 因为正数m 是2和8的等比中项，所以m 2＝16，则m ＝4，所以圆锥曲线x 2＋y 2m＝1即为椭圆x 2＋y 24＝1，易知其焦点坐标为(0，±3)，故选B.2．(2017·湖北荆门一模)已知θ是△ABC 的一个内角，且sin θ＋cos θ＝34，则方程x 2sin θ－y 2cos θ＝1表示( )A ．焦点在x 轴上的双曲线B ．焦点在y 轴上的双曲线C ．焦点在x 轴上的椭圆D ．焦点在y 轴上的椭圆 答案 D解析 因为(sin θ＋cos θ)2＝1＋2sin θcos θ＝916，所以sin θcos θ＝－732＜0，结合θ∈(0，π)，知sin θ>0，cos θ<0，又sin θ＋cos θ＝34＞0，所以sin θ＞－cos θ＞0，故1－cos θ＞1sin θ＞0，因为x 2sin θ－y 2cos θ＝1可化为y 2－1cos θ＋x 21sin θ＝1，所以方程x 2sin θ－y 2cos θ＝1表示焦点在y 轴上的椭圆．故选D.3．(2018·湖北八校联考)设F 1，F 2为椭圆x 29＋y 25＝1的两个焦点，点P 在椭圆上，若线段PF 1的中点在y 轴上，则|PF 2||PF 1|的值为( )A.514B.513C.49D.59答案 B解析 由题意知a ＝3，b ＝5，c ＝2.设线段PF 1的中点为M ，则有OM ∥PF 2，∵OM ⊥F 1F 2，∴PF 2⊥F 1F 2，∴|PF 2|＝b 2a ＝53.又∵|PF 1|＋|PF 2|＝2a ＝6，∴|PF 1|＝2a －|PF 2|＝133，∴|PF 2||PF 1|＝53×313＝513，故选B.4．(2017·全国卷Ⅲ)已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线bx －ay ＋2ab ＝0相切，则C 的离心率为( )A.63B.33C.23D.13答案 A解析 由题意知以A 1A 2为直径的圆的圆心为(0,0)，半径为a . 又直线bx －ay ＋2ab ＝0与圆相切， ∴圆心到直线的距离d ＝2aba 2＋b2＝a ，解得a ＝3b ，∴b a＝13，∴e ＝c a ＝a 2－b 2a＝1－⎝ ⎛⎭⎪⎫b a2＝1－⎝⎛⎭⎪⎫132＝63.故选A. 5．已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)与双曲线x 2m 2－y 2n2＝1(m >0，n >0)有相同的焦点(－c,0)和(c,0)，若c 是a ，m 的等比中项，n 2是2m 2与c 2的等差中项，则椭圆的离心率为( )A.32B.22C.12D.14答案 C解析 因为椭圆x 2a 2＋y 2b 2＝1(a >b >0)与双曲线x 2m 2－y 2n2＝1(m >0，n >0)有相同的焦点(－c,0)和(c,0)，所以c 2＝a 2－b 2＝m 2＋n 2.因为c 是a ，m 的等比中项，n 2是2m 2与c 2的等差中项，所以c 2＝am,2n 2＝2m 2＋c 2，所以m 2＝c 4a 2，n 2＝c 4a 2＋c 22，所以2c 4a 2＋c 22＝c 2，化为c 2a 2＝14，所以e ＝c a ＝12.故选C.6．(2017·荔湾区期末)某宇宙飞船运行的轨道是以地球中心为一焦点的椭圆，测得近地点距地面m 千米，远地点距地面n 千米，地球半径为r 千米，则该飞船运行轨道的短轴长为( )A ．2m ＋r n ＋r 千米 B.m ＋r n ＋r 千米C ．2mn 千米D ．mn 千米答案 A解析 ∵某宇宙飞船的运行轨道是以地球的中心F 2为一个焦点的椭圆， 设长半轴长为a ，短半轴长为b ，半焦距为c ， 则近地点A 距地心为a －c ，远地点B 距地心为a ＋c . ∴a －c ＝m ＋r ，a ＋c ＝n ＋r ， ∴a ＝m ＋n2＋r ，c ＝n －m2.又∵b 2＝a 2－c 2＝⎝ ⎛⎭⎪⎫m ＋n 2＋r 2－⎝ ⎛⎭⎪⎫n －m 22＝mn ＋(m ＋n )r ＋r 2＝(m ＋r )(n ＋r )．∴b ＝m ＋rn ＋r ， ∴短轴长为2b ＝2m ＋rn ＋r 千米，故选A.7．(2017·九江期末)如图，F 1，F 2分别是椭圆x 2a 2＋y 2b 2＝1(a >b >0)的两个焦点，A 和B 是以O 为圆心，以|OF 1|为半径的圆与该椭圆左半部分的两个交点，且△F 2AB 是等边三角形，则该椭圆的离心率为( )A.32B.12C.3－1D.22答案 C 解析 连接AF 1，∵F 1F 2是圆O 的直径，∴∠F 1AF 2＝90°， 即F 1A ⊥AF 2，又∵△F 2AB 是等边三角形，F 1F 2⊥AB ， ∴∠AF 2F 1＝12∠AF 2B ＝30°，因此，在Rt △F 1AF 2中，|F 1F 2|＝2c ，|F 1A |＝12|F 1F 2|＝c ，|F 2A |＝32|F 1F 2|＝3c .根据椭圆的定义，得2a ＝|F 1A |＋|F 2A |＝(1＋3)c ，解得a ＝1＋32c ，∴椭圆的离心率为e ＝c a＝3－1.故选C.8．(2018·郑州质检)椭圆x 25＋y 24＝1的左焦点为F ，直线x ＝a 与椭圆相交于点M ，N ，当△FMN 的周长最大时，△FMN 的面积是( )A.55B.655C.855D.455答案 C解析 设椭圆的右焦点为E ，由椭圆的定义知△FMN 的周长为L ＝|MN |＋|MF |＋|NF |＝|MN |＋(25－|ME |)＋(25－|NE |)．因为|ME |＋|NE |≥|MN |，所以|MN |－|ME |－|NE |≤0，当直线MN 过点E 时取等号，所以L ＝45＋|MN |－|ME |－|NE |≤45，即直线x ＝a 过椭圆的右焦点E 时，△FMN 的周长最大，此时S △FMN ＝12×|MN |×|EF |＝12×2×45×2＝855，故选C.9．如图所示，内外两个椭圆的离心率相同，从外层椭圆顶点向内层椭圆引切线AC ，BD ，设内层椭圆方程为x 2a 2＋y 2b 2＝1(a >b >0)，若直线AC 与BD 的斜率之积为－14，则椭圆的离心率为( )A.12 B.22C.32D.34答案 C解析 设外层椭圆方程为x 2ma 2＋y 2mb2＝1(a >b >0，m >1)，则切线AC 的方程为y ＝k 1(x－ma )，切线BD 的方程为y ＝k 2x ＋mb ，则由⎩⎪⎨⎪⎧y ＝k 1x －ma ，bx 2＋ay2＝a 2b 2，消去y ，得(b 2＋a 2k 21)x2－2ma 3k 21x ＋m 2a 4k 21－a 2b 2＝0.因为Δ＝(2ma 3k 21)2－4(b 2＋a 2k 21)(m 2a 4k 21－a 2b 2)＝0，整理，得k 21＝b 2a 2·1m 2－1.由⎩⎪⎨⎪⎧y ＝k 2x ＋mb ，bx 2＋ay 2＝a 2b 2，消去y ，得(b 2＋a 2k 22)x 2＋2a 2mbk 2x ＋a 2m 2b 2－a 2b 2＝0，因为Δ2＝(2a 2mbk 2)2－4×(b 2＋a 2k 22)(a 2m 2b 2－a 2b 2)＝0，整理，得k 22＝b 2a2·(m 2－1)．所以k 21·k 22＝b 4a 4.因为k 1k 2＝－14，所以b 2a 2＝14，e 2＝c 2a 2＝a 2－b 2a 2＝34，所以e ＝32，故选C.10．(2018·永康市模拟)设椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)和圆x 2＋y 2＝b 2，若椭圆C 上存在点P ，使得过点P 引圆O 的两条切线，切点分别为A ，B ，满足∠APB ＝60°，则椭圆的离心率e 的取值范围是( )A ．0<e ≤32B.12≤e <1 C.32<e <1 D.32≤e <1 答案 D解析 由椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)焦点在x 轴上，连接OA ，OB ，OP ，依题意，O ，P ，A ，B 四点共圆， ∵∠APB ＝60°，∠APO ＝∠BPO ＝30°， 在直角三角形OAP 中，∠AOP ＝60°，∴cos ∠AOP ＝b |OP |＝12，∴|OP |＝b12＝2b ，∴b <|OP |≤a ，∴2b ≤a ，∴4b 2≤a 2， 由a 2＝b 2＋c 2，即4(a 2－c 2)≤a2，∴3a 2≤4c 2，即c 2a 2≥34，∴e ≥32，又0<e <1，∴32≤e <1， ∴椭圆C 的离心率的取值范围是32≤e <1.故选D. 二、填空题11．(2017·湖南东部六校联考)设P ，Q 分别是圆x 2＋(y －1)2＝3和椭圆x 24＋y 2＝1上的点，则P ，Q 两点间的最大距离是________．答案733解析 依据圆的性质可知，P ，Q 两点间的最大距离可以转化为圆心到椭圆上点的距离的最大值加上圆的半径3，设Q (x ，y )，则圆心(0,1)到椭圆上点的距离为d ＝x 2＋y －2＝－3y 2－2y ＋5＝－3⎝ ⎛⎭⎪⎫y ＋132＋163，∵－1≤y ≤1，∴当y ＝－13时，d 取最大值433，所以P ，Q 两点间的最大距离为d max ＋3＝733. 12．(2018·广州二测)已知中心在坐标原点的椭圆C 的右焦点为F (1,0)，点F 关于直线y ＝12x 的对称点在椭圆C 上，则椭圆C 的方程为________．答案 5x 29＋5y 24＝1解析 设F (1,0)关于直线y ＝12x 的对称点为(x ，y )，则⎩⎪⎨⎪⎧0＋y 2＝12×1＋x2，y －0x －1×12＝－1，解得⎩⎪⎨⎪⎧x ＝35，y ＝45，由于椭圆的两个焦点为(－1,0)，(1,0)，所以2a ＝⎝ ⎛⎭⎪⎫35－12＋⎝ ⎛⎭⎪⎫452＋⎝ ⎛⎭⎪⎫35＋12＋⎝ ⎛⎭⎪⎫452＝655，a ＝355，又c ＝1，所以b 2＝a 2－c 2＝95－1＝45，所以椭圆C 的方程为x 295＋y 245＝1，即5x 29＋5y24＝1. 13．(2018·江西五市联考)已知椭圆x 2a 2＋y 2b2＝1(a >b >0)，A ，B 为椭圆上的两点，线段AB的垂直平分线交x 轴于点M ⎝ ⎛⎭⎪⎫a5，0，则椭圆的离心率e 的取值范围是________． 答案 ⎝⎛⎭⎪⎫55，1解析 设A (x 1，y 1)，B (x 2，y 2)，x 1≠x 2，则⎩⎪⎨⎪⎧ ⎝ ⎛⎭⎪⎫x 1－a 52＋y 21＝⎝ ⎛⎭⎪⎫x 2－a 52＋y 22，x 21a 2＋y21b 2＝1，x 22a 2＋y 22b 2＝1，即⎩⎪⎨⎪⎧2a 5x 1－x 2＝x 21－x 22＋y 21－y 22，y 21＝b 2－b2a 2x 21，y 22＝b 2－b 2a2x 22，所以2a 5(x 1－x 2)＝a 2－b 2a2(x 21－x 22)，所以2a3a 2－b 2＝x 1＋x 2.又－a ≤x 1≤a ，－a ≤x 2≤a ，x 1≠x 2，所以－2a <x 1＋x 2<2a ，则2a 3a 2－b 2<2a ，即b 2a 2<45，所以e 2>15.又0<e <1，所以55<e <1.14．(2016·江苏高考)如图，在平面直角坐标系xOy 中，F 是椭圆x 2a 2＋y 2b2＝1(a >b >0)的右焦点，直线y ＝b2与椭圆交于B ，C 两点，且∠BFC＝90°，则该椭圆的离心率是________．答案63解析 由已知条件易得B ⎝ ⎛⎭⎪⎫－32a ，b 2，C ⎝ ⎛⎭⎪⎫32a ，b 2，F (c,0)， ∴BF →＝⎝ ⎛⎭⎪⎫c ＋32a ，－b 2，CF →＝⎝ ⎛⎭⎪⎫c －32a ，－b 2，由∠BFC ＝90°，可得BF →·CF →＝0， 所以⎝ ⎛⎭⎪⎫c －32a ⎝ ⎛⎭⎪⎫c ＋32a ＋⎝ ⎛⎭⎪⎫－b 22＝0，c 2－34a 2＋14b 2＝0，即4c 2－3a 2＋(a 2－c 2)＝0，亦即3c 2＝2a 2，所以c 2a 2＝23，则e ＝c a ＝63.B 级三、解答题15．(2018·安徽合肥三校联考)已知椭圆的中心在原点，焦点在x 轴上，离心率为22，且椭圆经过圆C ：x 2＋y 2－4x ＋22y ＝0的圆心C .(1)求椭圆的方程；(2)设直线l 过椭圆的焦点且与圆C 相切，求直线l 的方程． 解 (1)圆C 方程化为(x －2)2＋(y ＋2)2＝6， 圆心C (2，－2)，半径r ＝ 6.设椭圆的方程为x 2a 2＋y 2b2＝1(a >b >0)，则⎩⎪⎨⎪⎧4a 2＋2b2＝1，1－⎝ ⎛⎭⎪⎫b a 2＝⎝ ⎛⎭⎪⎫222，所以⎩⎪⎨⎪⎧a 2＝8，b 2＝4.所以所求的椭圆方程是x 28＋y 24＝1.(2)由(1)得椭圆的左、右焦点分别是F 1(－2,0)，F 2 (2,0)， |F 2C |＝－2＋＋22＝2<r ＝ 6.F 2在圆C 内，故过F 2没有圆C 的切线，所以直线l 过焦点F 1.设l 的方程为y ＝k (x ＋2)，即kx －y ＋2k ＝0， 点C (2，－2)到直线l 的距离为d ＝|2k ＋2＋2k |1＋k 2， 由d ＝6，得|2k ＋2＋2k |1＋k 2＝ 6. 化简，得5k 2＋42k －2＝0，解得k ＝25或k ＝－ 2. 故l 的方程为2x －5y ＋22＝0或2x ＋y ＋22＝0.16．(2018·陕西咸阳模拟)在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)过点P (2,1)，且离心率e ＝32. (1)求椭圆C 的方程；(2)直线l 的斜率为12，直线l 与椭圆C 交于A ，B 两点．求△PAB 面积的最大值．解 (1)∵e 2＝c 2a 2＝a 2－b 2a 2＝34，∴a 2＝4b 2.又椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)过点P (2,1)，∴4a 2＋1b2＝1.∴a 2＝8，b 2＝2.故所求椭圆方程为x 28＋y 22＝1.(2)设l 的方程为y ＝12x ＋m ，点A (x 1，y 1)，B (x 2，y 2)，联立⎩⎪⎨⎪⎧y ＝12x ＋m ，x 28＋y22＝1，整理得x 2＋2mx ＋2m 2－4＝0.∵Δ＝4m 2－8m 2＋16>0，解得|m |<2. ∴x 1＋x 2＝－2m ，x 1x 2＝2m 2－4. 则|AB |＝1＋14× x 1＋x 22－4x 1x 2＝ －m2.点P 到直线l 的距离d ＝ |m |1＋14＝2|m |5. ∴S △PAB ＝12d |AB |＝12×2|m |5×－m2＝m2－m2≤m 2＋4－m 22＝2.而且仅当m 2＝2，即m ＝±2时取得最大值． ∴△PAB 面积的最大值为2.17．(2018·兰州模拟)已知椭圆C 的中心在坐标原点，焦点在x 轴上，左顶点为A ，左焦点为F 1(－2,0)，点B (2，2)在椭圆C 上，直线y ＝kx (k ≠0)与椭圆C 交于P ，Q 两点，直线AP ，AQ 分别与y 轴交于点M ，N .(1)求椭圆C 的方程；(2)以MN 为直径的圆是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．解 (1)设椭圆C 的方程为x 2a 2＋y 2b2＝1(a >b >0)，∵椭圆的左焦点为F 1(－2,0)，∴a 2－b 2＝4. ∵点B (2，2)在椭圆C 上，∴4a 2＋2b2＝1，解得a 2＝8，b 2＝4， ∴椭圆C 的方程为x 28＋y 24＝1.(2)依题意点A 的坐标为(－22，0)，设P (x 0，y 0)(不妨设x 0>0)，则Q (－x 0，－y 0)，由⎩⎪⎨⎪⎧y ＝kx ，x 28＋y24＝1，得x 0＝221＋2k2，y 0＝22k 1＋2k2，∴直线AP 的方程为y ＝k1＋1＋2k 2(x ＋22)， 直线AQ 的方程为y ＝k1－1＋2k 2(x ＋22)， ∴M ⎝ ⎛⎭⎪⎫0，22k 1＋1＋2k 2，N ⎝ ⎛⎭⎪⎫0，22k 1－1＋2k 2，∴|MN |＝⎪⎪⎪⎪⎪⎪22k1＋1＋2k 2－22k 1－1＋2k 2＝2＋2k 2|k |.设MN 的中点为E ，则点E 的坐标为⎝⎛⎭⎪⎫0，－2k ，则以MN 为直径的圆的方程为x 2＋⎝ ⎛⎭⎪⎫y ＋2k 2＝＋2k2k2，即x 2＋y 2＋22ky ＝4，令y ＝0得x ＝2或x ＝－2，即以MN 为直径的圆经过两定点P 1(－2,0)，P 2(2,0)．18．(2018·湖南十校联考)如图，设点A ，B 的坐标分别为(－3，0)，(3，0)，直线AP ，BP 相交于点P ，且它们的斜率之积为－23.(1)求点P 的轨迹方程；(2)设点P 的轨迹为C ，点M ，N 是轨迹C 上不同于A ，B 的两点，且满足AP ∥OM ，BP ∥ON ，求证：△MON 的面积为定值．解 (1)设点P 的坐标为(x ，y )，由题意得，k AP ·k BP ＝y x ＋3·y x －3＝－23(x ≠±3)，化简得，点P 的轨迹方程为x 23＋y 22＝1(x ≠±3)． (2)证明：由题意知，M ，N 是椭圆C 上不同于A ，B 的两点，且AP ∥OM ，BP ∥ON ，则直线11 AP ，BP 的斜率必存在且不为0.因为AP ∥OM ，BP ∥ON ，所以k OM ·k ON ＝k AP ·k BP ＝－23. 设直线MN 的方程为x ＝my ＋t ，代入椭圆方程x 23＋y 22＝1，得(3＋2m 2)y 2＋4mty ＋2t 2－6＝0，①设M ，N 的坐标分别为(x 1，y 1)，(x 2，y 2)，则y 1，y 2是方程①的两根，所以y 1＋y 2＝－4mt 3＋2m 2，y 2y 2＝2t 2－63＋2m 2.又k OM ·k ON ＝y 1y 2x 1x 2＝y 1y 2m 2y 1y 2＋mt y 1＋y 2＋t 2＝2t 2－63t 2－6m 2，所以2t 2－63t 2－6m 2＝－23，即2t 2＝2m 2＋3.又S △MON ＝12|t ||y 1－y 2|＝12·|t |－24t 2＋48m2＋723＋2m 2，所以S △MON ＝26t 24t 2＝62，即△MON 的面积为定值62.。

第3节椭圆基础巩固(时间:30分钟)1.(2017·泉州质检)已知椭圆+=1的长轴在x轴上,焦距为4,则m等于( A )(A)8 (B)7 (C)6 (D)5解析:因为椭圆+=1的长轴在x轴上,所以解得6<m<10.因为焦距为4,所以c2=m-2-10+m=4,解得m=8.2.椭圆+=1的离心率为,则k的值为( C )(A)-21 (B)21 (C)-或21 (D)或21解析:若a2=9,b2=4+k,则c=,由=,即=,得k=-;若a2=4+k,b2=9,则c=,由=,即=,解得k=21.故选C.3.椭圆+=1上一点M到焦点F1的距离为2,N是MF1的中点,则|ON|等于( B )(A)2 (B)4 (C)8 (D)解析:如图,连接MF2,已知|MF1|=2,又|MF1|+|MF2|=10,所以|MF2|=10-|MF1|=8.由题意知|ON|=|MF2|=4.故选B.4.(2017·玉林市一模)如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( B )(A) (B) (C) (D)解析:不妨设椭圆方程为+=1(a>b>0),由球筒的轴截面图形得椭圆的长轴长为AD=AC+CD=AF+EA=EF=20-4,短轴长为球筒的直径4,所以解得a=8,b=2,所以c==2,所以该椭圆的离心率为e===.故选B.5.若点O和点F分别为椭圆+=1的中心和左焦点,点P为椭圆上的任意一点,则·的最大值为( C )(A)2 (B)3 (C)6 (D)8解析:由椭圆+=1,可得点F(-1,0),点O(0,0),设P(x,y),-2≤x≤2,则·=(x,y)·(x+1,y)=x2+x+y2=x2+x+3(1-)=x2+x+3= (x+2)2+2,当且仅当x=2时,·取得最大值6.故选C.6.(2017·宁夏中卫市二模)椭圆C:+=1(a>b>0)上的任意一点M到两个焦点的距离和是4,椭圆的焦距是2,则椭圆C的标准方程是.解析:椭圆C:+=1(a>b>0)上的任意一点M到两个焦点的距离和是4,焦距是2,则有2a=4,2c=2,即a=2,c=1,所以b2=a2-c2=3,椭圆的标准方程为+=1.答案:+=17.(2017·西安市一模)已知△ABC的顶点A(-3,0)和顶点B(3,0),顶点C在椭圆+=1上,则= .解析:由椭圆+=1知长轴长2a=10,短轴长2b=8,焦距2c=6,则顶点A,B为椭圆的两个焦点.如图△ABC中,|AB|=6,|BC|+|AC|=10,由正弦定理可知===2R,所以=,即=,则==3.答案:3能力提升(时间:15分钟)8.(2017·怀化市四模)“神舟”五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球的最近距离为d1,到地球的最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在“神舟”飞船运行轨道的另外一个焦点上,若在此焦点上发射某种信号,需要飞行中的航天员中转后地球人才能接收到,则信号传导到地球人的最短距离为( D )(A)d1+d2+R (B)d2-d1+2R(C)d2+d1-2R (D)d1+d2解析:设椭圆的方程为+=1(a>b>0),半焦距为c,两焦点分别为F1,F2,运行中的航天员为P,由已知得则2a=d1+d2+2R,最短距离为|PF1|+|PF2|-2R=2a-2R=d1+d2.故选D.9.(2017·广州一模)已知F1,F2分别是椭圆C:+=1(a>b>0)的左、右焦点,椭圆C上存在点P使∠F1PF2为钝角,则椭圆C的离心率的取值范围是( A )(A)(,1) (B)(,1)(C)(0,) (D)(0,)解析:法一设P(x0,y0),则|x0|<a,又F1(-c,0),F2(c,0),且∠F1PF2为钝角,当且仅当·<0有解,即(-c-x0,-y0)·(c-x0,-y0)=(-c-x0)(c-x0)+<0,即有c2>+有解,即c2>(+)min.当(+)最小时|PO|=最小,此时点P为短轴端点,所以(+)min=b2,所以c2>b2,c2>a2-c2,所以>,即e>.又0<e<1,所以<e<1.故选A.法二由椭圆图形知,短轴端点对两焦点的张角∠F1BF2最大,需满足题意,这个张角的范围是(90°,180°),如图.当这个角为90°时,△F1BF2为等腰直角三角形,大于90°时,∠BF2O<45°,所以e==cos∠BF2O>cos 45°=,结合e<1得<e<1.故选A.10.(2017·泰州市模拟)已知点F,A是椭圆C:+=1的左焦点和上顶点,若点P是椭圆C 上一动点,则△PAF周长的最大值为.解析:设椭圆右焦点为F2,椭圆C:+=1,a=4,由椭圆的定义|PF|+|PF2|=2a=8,|AF|+|AF2|=2a=8,所以△PAF周长为|AF|+|PF|+|PA|≤|AF|+|PF|+|PF2|+|AF2|=4a=16,当且仅当AP过F2时△PAF周长取最大值,所以△PAF周长的最大值为16.答案:1611.(2017·张家界一模)已知A,B,F分别是椭圆x2+=1(0<b<1)的右顶点、上顶点、左焦点,设△ABF的外接圆的圆心坐标为(p,q).若p+q>0,则椭圆的离心率的取值范围为.解析:如图所示,线段FA的垂直平分线为x=,线段AB的中点(,).因为k AB=-b,所以线段AB的垂直平分线的斜率k=,所以线段AB的垂直平分线方程为y-= (x-).把x==p代入上述方程可得y==q.因为p+q>0,所以+>0,化为b>.又0<b<1,解得<b2<1,即-1<-b2<-,所以0<1-b2<,所以e==c=∈(0,).答案:(0,)12.(2017·兰州模拟)已知椭圆C:+=1(a>b>0)的一个顶点为A(2,0),离心率为.直线y=k(x-1)与椭圆C交于不同的两点M,N.(1)求椭圆C的方程;(2)当△AMN的面积为时,求k的值.解:(1)由题意得解得b=,所以椭圆C的方程为+=1.(2)由得(1+2k2)x2-4k2x+2k2-4=0.设点M, N的坐标分别为(x1,y1),(x2,y2),则y1=k(x1-1),y2=k(x2-1),x1+x2=,x1x2=,所以|MN|===.又因为点A(2,0)到直线y=k(x-1)的距离d=,所以△AMN的面积为S=|MN|·d=,由=,解得k=±1.13.(2017·深圳市一模)已知椭圆C:+=1(a>b>0)的左右顶点分别为A1,A2,上下顶点分别为B2,B1,左右焦点分别为F1,F2,其中长轴长为4,且圆O:x2+y2=为菱形A1B1A2B2的内切圆.(1)求椭圆C的方程;(2)点N(n,0)为x轴正半轴上一点,过点N作椭圆C的切线l,记右焦点F2在l上的射影为H,若△F1HN的面积不小于n2,求n的取值范围.解: (1)由题意知2a=4,所以a=2,所以A1(-2,0),A2(2,0),因为B1(0,-b),B2(0,b),所以直线A2B2的方程为+=1,即bx+2y-2b=0,所以=,解得b2=3,故椭圆C的方程为+=1.(2)由题意,可设直线l的方程为x=my+n,m≠0,联立消去x得(3m2+4)y2+6mny+3(n2-4)=0.由直线l与椭圆C相切,得Δ=(6mn)2-4×3×(3m2+4)(n2-4) =0,化简得3m2-n2+4=0.(*)设点H(mt+n,t),由(1)知F1(-1,0),F2(1,0),则·=-1,解得t=-,所以△F1HN的面积= (n+1) -=,把*式代入,消去n化简得=|m|,所以|m|≥n2=(3m2+4),解得≤|m|≤2,即≤m2≤4,从而≤≤4,又n>0,所以≤n≤4,故n的取值范围为[,4].14.(2017·淮北市一模)已知椭圆C1:+=1(a>b>0)的离心率e=,且过点(2,),直线l1:y=kx+m(m>0)与圆C2:(x-1)2+y2=1相切且与椭圆C1交于A,B两点.(1)求椭圆C1的方程;(2)过原点O作l1的平行线l2交椭圆于C,D两点,设|AB|=λ|CD|,求λ的最小值.解:(1)由题意得结合a2=b2+c2,解得a=4,b=2,故椭圆C1的标准方程为+=1.(2)联立得(1+4k2)x2+8kmx+4(m2-4)=0,Δ>0恒成立,设A(x1,y1),B(x2,y2),则得|x1-x2|=,所以|AB|=·,把l2:y=kx代入C1:+=1,得x3,4=,所以|CD|=|x3-x4|=·,所以λ===,又直线l1与圆C2相切,所以d==1,平方化为k=.所以λ===≥, 当m=,k=-时,λ取最小值.。

第五节椭__圆1．椭圆的定义平面内到两定点F1，F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆．两定点F1，F2叫做椭圆的焦点．集合P＝{M||MF1|＋|MF2|＝2a}，|F1F2|＝2c，其中a＞0，c＞0，且a，c为常数．(1)当2a＞|F1F2|时，P点的轨迹是椭圆；(2)当2a＝|F1F2|时，P点的轨迹是线段；(3)当2a＜|F1F2|时，P点不存在．2．椭圆的标准方程和几何性质x∈[－a，a]，y∈[－b，x∈[－b，b]，1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面内与两个定点F1，F2的距离之和等于常数的点的轨迹是椭圆．()(2)椭圆上一点P与两焦点F1，F2构成△PF1F2的周长为2a＋2c(其中a为椭圆的长半轴长，c 为椭圆的半焦距)．( )(3)椭圆的离心率e 越大，椭圆就越圆．( )(4)方程mx 2＋ny 2＝1(m >0，n >0，m ≠n )表示的曲线是椭圆．( ) (5)y 2a 2＋x 2b 2＝1(a ≠b )表示焦点在y 轴上的椭圆．( ) (6)x 2a 2＋y 2b 2＝1(a >b >0)与y 2a 2＋x 2b 2＝1(a >b >0)的焦距相等．( ) 答案：(1)× (2)√ (3)× (4)√ (5)× (6)√2．椭圆C ：x 225＋y 216＝1的左、右焦点分别为F 1，F 2，过F 2的直线交椭圆C 于A ，B 两点，则△F 1AB 的周长为( )A ．12B ．16C ．20D ．24解析：选C △F 1AB 的周长为 |F 1A |＋|F 1B |＋|AB |＝|F 1A |＋|F 2A |＋|F 1B |＋|F 2B | ＝2a ＋2a ＝4a .在椭圆x 225＋y 216＝1中，a 2＝25，a ＝5，∴△F 1AB 的周长为4a ＝20，故选C.3．若方程x 25－k ＋y 2k －3＝1表示椭圆，则k 的取值范围是________．解析：由已知得⎩⎪⎨⎪⎧5－k >0，k －3>0，5－k ≠k －3.解得3<k <5且k ≠4. 答案：(3,4)∪(4,5)4．设e 是椭圆x 24＋y 2k ＝1的离心率，且e ＝23，则实数k 的值是________．解析：当k ＞4 时，有e ＝1－4k ＝23，解得k ＝365；当0＜k ＜4时，有e ＝ 1－k4＝23，解得k ＝209.故实数k 的值为209或365. 答案：209或3655．(教材习题改编)已知椭圆的一个焦点为F (1,0)，离心率为12，则椭圆的标准方程为________．解析：设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)．因为椭圆的一个焦点为F (1,0)，离心率e ＝12，所以⎩⎪⎨⎪⎧c ＝1，c a ＝12，a 2＝b 2＋c 2，解得⎩⎪⎨⎪⎧a ＝2c ＝2，b 2＝3，故椭圆的标准方程为x 24＋y 23＝1.答案：x 24＋y 23＝1考点一 椭圆的标准方程 (基础送分型考点——自主练透)[考什么·怎么考]A.x 25＋y 2＝1 B.x 24＋y 25＝1C.x 25＋y 2＝1或x 24＋y 25＝1 D ．以上答案都不对解析：选C 直线x －2y ＋2＝0与坐标轴的交点为(0,1)，(－2,0)， 由题意知当焦点在x 轴上时，c ＝2，b ＝1， ∴a 2＝5，所求椭圆的标准方程为x 25＋y 2＝1.当焦点在y 轴上时，b ＝2，c ＝1， ∴a 2＝5，所求椭圆的标准方程为y 25＋x 24＝1.2．(2018·合肥一模)已知椭圆x 29＋y 25＝1，F 为其右焦点，A 为其左顶点，P 为该椭圆上的动点，则能够使PA ―→·PF ―→＝0的点P 的个数为( )A ．4B ．3C ．2D ．1解析：选B 由题意知F (2,0)，A (－3，0)．当点P 与点A 重合时，显然PA ―→·PF ―→＝0，此时P (－3，0)．当点P 与点A 不重合时，设P (x ，y )，PA ―→·PF ―→＝0⇔PA ⊥PF ，即点P 在以AF 为直径的圆上，则圆的方程为⎝⎛⎭⎫x ＋122＋y 2＝254. ① 又点P 在椭圆上， 所以x 29＋y 25＝1. ②由①②消去y 得4x 2＋9x －9＝0，解得x ＝－3(舍去)或34，则y ＝±534，故能够使PA ―→·PF―→＝0的点P 的个数为3，故选B.3．一个椭圆的中心在原点，焦点F 1，F 2在x 轴上，P (2，3)是椭圆上一点，且|PF 1|，|F 1F 2|，|PF 2|成等差数列，则椭圆的标准方程为________________．解析：设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)．由点P (2，3)在椭圆上，知4a 2＋3b 2＝1.又|PF 1|，|F 1F 2|，|PF 2|成等差数列， 则|PF 1|＋|PF 2|＝2|F 1F 2|， 即2a ＝2×2c ，则a ＝2c ，又c 2＝a 2－b 2，联立⎩⎪⎨⎪⎧4a 2＋3b 2＝1，c 2＝a 2－b 2，a ＝2c得a 2＝8，b 2＝6，故椭圆的标准方程为x 28＋y 26＝1.答案：x 28＋y 26＝14．椭圆C 的中心在原点，焦点在x 轴上，若椭圆C 的离心率等于12，且它的一个顶点恰好是抛物线x 2＝83y 的焦点，则椭圆C 的标准方程为______________．解析：由题意设椭圆的方程为x 2a 2＋y 2b2＝1(a ＞b ＞0)．由题设知抛物线的焦点为(0,23)，所以椭圆中b ＝2 3.因为e ＝c a ＝12，所以a ＝2c ，又a 2－b 2＝c 2，联立解得c ＝2，a ＝4，所以椭圆C 的标准方程为x 216＋y 212＝1.答案：x 216＋y 212＝1[怎样快解·准解]1．定义法求椭圆的标准方程根据椭圆的定义确定a 2，b 2的值，再结合焦点位置求出椭圆的方程．其中常用的关系有：(1)b 2＝a 2－c 2；(2)椭圆上任意一点到椭圆两焦点的距离之和等于2a ； (3)椭圆上一短轴顶点到一焦点的距离等于实半轴长a . 2．待定系数法求椭圆的标准方程的4步骤[注意] 求椭圆的方程时，要“先定型，再定量”，不能确定焦点的位置时，可进行分类讨论或把椭圆的方程设为mx 2＋ny 2＝1(m >0，n >0)．(如第1题)考点二 椭圆的定义及其应用 (重点保分型考点——师生共研)1．已知△ABC 的顶点B ，C 在椭圆x 23＋y 2＝1上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC 边上，则△ABC 的周长是( )A ．23B ．6C ．4 3D ．12解析：选C 由椭圆的方程得a ＝ 3.设椭圆的另一个焦点为F ，则由椭圆的定义得|BA |＋|BF |＝|CA |＋|CF |＝2a ，所以△ABC 的周长为|BA |＋|BC |＋|CA |＝|BA |＋|BF |＋|CF |＋|CA |＝(|BA |＋|BF |)＋(|CF |＋|CA |)＝2a ＋2a ＝4a ＝4 3.2．若F 1，F 2是椭圆x 29＋y 27＝1的两个焦点，A 为椭圆上一点，且∠AF 1F 2＝45°，则△AF 1F 2的面积为( )A ．7 B.74C.72D.752解析：选C 由题意得a ＝3，b ＝7，c ＝2， ∴|F 1F 2|＝22，|AF 1|＋|AF 2|＝6.∵|AF 2|2＝|AF 1|2＋|F 1F 2|2－2|AF 1|·|F 1F 2|cos 45° ＝|AF 1|2－4|AF 1|＋8，∴(6－|AF 1|)2＝|AF 1|2－4|AF 1|＋8. 解得|AF 1|＝72.∴△AF 1F 2的面积S ＝12×72×22×22＝72.[解题师说]1．利用定义求方程、焦点三角形及最值的方法2．与椭圆定义有关的结论以椭圆x 2a 2＋y 2b 2＝1(a >b >0)上一点P (x 0，y 0)(y 0≠0)和焦点F 1(－c,0)，F 2(c,0)为顶点的△PF 1F 2中，若∠F 1PF 2＝θ，则(1)|PF 1|＋|PF 2|＝2a .(2)4c 2＝|PF 1|2＋|PF 2|2－2|PF 1||PF 2|·cos θ.(3)S △PF 1F 2＝12|PF 1||PF 2|·sin θ，当|y 0|＝b ，即P 为短轴端点时，S △PF 1F 2取最大值，为bc .(4)焦点三角形的周长为2(a ＋c )．[冲关演练]1．已知椭圆C ：x 24＋y 23＝1，M ，N 是坐标平面内的两点，且M 与C 的焦点不重合．若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则|AN |＋|BN |＝( )A ．4B ．8C ．12D ．16解析：选B 设MN 的中点为D ，椭圆C 的左、右焦点分别为F 1，F 2，如图，连接DF 1，DF 2，因为F 1是MA 的中点，D 是MN 的中点，所以F 1D 是△MAN 的中位线，则|DF 1|＝12|AN |，同理|DF 2|＝12|BN |，所以|AN |＋|BN |＝2(|DF 1|＋|DF 2|)，因为D 在椭圆上，所以根据椭圆的定义知|DF 1|＋|DF 2|＝4，所以|AN |＋|BN |＝8.2．已知F 1，F 2是椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的两个焦点，P 为椭圆C 上的一点，且PF 1―→⊥PF 2―→.若△PF 1F 2的面积为9，则b ＝________.解析：由题意知|PF 1|＋|PF 2|＝2a ，PF 1―→⊥PF 2―→， 所以|PF 1|2＋|PF 2|2＝|F 1F 2|2＝4c 2， 所以(|PF 1|＋|PF 2|)2－2|PF 1||PF 2|＝4c 2， 所以2|PF 1||PF 2|＝4a 2－4c 2＝4b 2. 所以|PF 1||PF 2|＝2b 2，所以S △PF 1F 2＝12|PF 1||PF 2|＝12×2b 2＝b 2＝9.所以b ＝3. 答案：3考点三 椭圆的几何性质 (题点多变型考点——追根溯源)角度(一) 求椭圆离心率的值(或范围)1．从椭圆x 2a 2＋y 2b 2＝1(a >b >0)上一点P 向x 轴作垂线，垂足恰为左焦点F 1，A 是椭圆与x 轴正半轴的交点，B 是椭圆与y 轴正半轴的交点，且AB ∥OP (O 是坐标原点)，则该椭圆的离心率是( )A.24 B.12C.22D.32解析：选C 由题意可设P (－c ，y 0)(c 为半焦距)，k OP ＝－y 0c ，k AB ＝－ba ，由于OP ∥AB ，∴－y 0c ＝－b a ，y 0＝bc a ，把P ⎝⎛⎭⎫－c ，bc a 代入椭圆方程得(－c )2a 2＋⎝⎛⎭⎫bc a 2b 2＝1，即⎝⎛⎭⎫c a 2＝12，∴e ＝c a ＝22. [题型技法] 求椭圆离心率的方法(1)定义法：根据条件求出a ，c ，直接利用公式e ＝ca求解．(2)方程法：根据已知条件建立关于a ，b ，c 的齐次式，然后转化为关于e 的方程求解． [注意] 在解关于离心率问题时，注意根据椭圆离心率e ∈(0,1)进行根的取舍．角度(二) 根据椭圆性质求参数的值(或范围)2．(2017·全国卷Ⅰ)设A ，B 是椭圆C ：x 23＋y 2m ＝1长轴的两个端点．若C 上存在点M满足∠AMB ＝120°，则m 的取值范围是( )A ．(0,1]∪[9，＋∞)B ．(0， 3 ]∪[9，＋∞)C ．(0,1]∪[4，＋∞)D ．(0， 3 ]∪[4，＋∞)解析：选A 当0＜m ＜3时，焦点在x 轴上， 要使C 上存在点M 满足∠AMB ＝120°， 则a b ≥tan 60°＝3，即3m ≥3，解得0＜m ≤1.当m ＞3时，焦点在y 轴上，要使C 上存在点M 满足∠AMB ＝120°，则a b ≥tan 60°＝3，即m3≥3，解得m ≥9.故m 的取值范围为(0,1]∪[9，＋∞)．[题“根”探求]1．无论题型如何变化，都是围绕椭圆的几何性质，外加其他条件来考查，所以理清椭圆的几个关键点(顶点、原点、焦点、对称轴)和灵活应用几个公式⎝⎛⎭⎫e ＝c a ＝ 1－⎝⎛⎭⎫b a 2，a 2＝b 2＋c 2，理清a ，b ，c 的内在联系(a ，b ，c 的关系式―→构造a ，c 的齐次方程或不等式)，便可以不变应万变．2．与椭圆几何性质有关的问题要结合图形进行分析，即使画不出图形，思考时也要联想到一个图形．3．与椭圆有关的范围或最值问题常常涉及一些不等式．例如－a ≤x ≤a ，－b ≤y ≤b,0＜e ＜1，所以在求与椭圆有关的相关量的范围时，要注意应用这些不等关系．[冲关演练]1．过椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左焦点F 1作x 轴的垂线交椭圆于点P ，F 2为椭圆的右焦点，若∠F 1PF 2＝60°，则椭圆的离心率为( )A.22B.33C.12D.13解析：选B 由题意，可设P ⎝⎛⎭⎫－c ，b 2a . 因为在Rt △PF 1F 2中，|PF 1|＝b 2a ，|F 1F 2|＝2c ，∠F 1PF 2＝60°，所以2acb 2＝ 3.又因为b 2＝a 2－c 2，所以3c 2＋2ac －3a 2＝0，即3e 2＋2e －3＝0，解得e ＝33或e ＝－3，又因为e ∈(0,1)，所以e ＝33. 2．已知F 1，F 2分别是椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，若椭圆C 上存在点P ，使得线段PF 1的中垂线恰好经过焦点F 2，则椭圆C 离心率的取值范围是( )A.⎣⎡⎭⎫23，1B.⎣⎡⎦⎤13，22 C.⎣⎡⎭⎫13，1D.⎝⎛⎦⎤0，13解析：选C 如图所示， ∵线段PF 1的中垂线经过F 2，∴|PF 2|＝|F 1F 2|＝2c ， 即椭圆上存在一点P ， 使得|PF 2|＝2c .∴a －c ≤2c ≤a ＋c .∴e ＝c a ∈⎣⎡⎭⎫13，1. 3．已知椭圆x 29＋y 24－k ＝1的离心率为45，则k ＝________.解析：当9＞4－k ＞0，即－5<k <4时， a ＝3，c 2＝9－(4－k )＝5＋k ， ∴5＋k 3＝45，解得k ＝1925. 当9＜4－k ，即k ＜－5时，a ＝4－k ，c 2＝－k －5， ∴－k －54－k ＝45，解得k ＝－21，所以k 的值为1925或－21.答案：1925或－21考点四 直线与椭圆的位置关系 (重点保分型考点——师生共研)设椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左焦点为F ，离心率为33，过点F 且与x 轴垂直的直线被椭圆截得的线段长为433.(1)求椭圆的方程；(2)设A ，B 分别为椭圆的左、右顶点，过点F 且斜率为k 的直线与椭圆交于C ，D 两点，若AC ―→·DB ―→＋AD ―→·CB ―→＝8，O 为坐标原点，求△OCD 的面积．解：(1)因为过焦点且垂直于长轴的直线被椭圆截得的线段长为433，所以2b 2a ＝433.因为椭圆的离心率为33，所以c a ＝33， 又a 2＝b 2＋c 2，可解得b ＝2，c ＝1，a ＝ 3.所以椭圆的方程为x 23＋y 22＝1.(2)由(1)可知F (－1,0)，则直线CD 的方程为y ＝k (x ＋1)． 联立⎩⎪⎨⎪⎧y ＝k (x ＋1)，x 23＋y 22＝1，消去y 得(2＋3k 2)x 2＋6k 2x ＋3k 2－6＝0. 设C (x 1，y 1)，D (x 2，y 2)，所以x 1＋x 2＝－6k 22＋3k 2，x 1x 2＝3k 2－62＋3k 2.又A (－3，0)，B (3，0)， 所以AC ―→·DB ―→＋AD ―→·CB ―→＝(x 1＋3，y 1)·(3－x 2，－y 2)＋(x 2＋3，y 2)·(3－x 1，－y 1) ＝6－2x 1x 2－2y 1y 2＝6－2x 1x 2－2k 2(x 1＋1)(x 2＋1) ＝6－(2＋2k 2)x 1x 2－2k 2(x 1＋x 2)－2k 2 ＝6＋2k 2＋122＋3k 2＝8，解得k ＝±2. 从而x 1＋x 2＝－6×22＋3×2＝－32，x 1x 2＝3×2－62＋3×2＝0.所以|x 1－x 2|＝(x 1＋x 2)2－4x 1x 2 ＝⎝⎛⎭⎫－322－4×0＝32，|CD |＝1＋k 2|x 1－x 2|＝1＋2×32＝332.而原点O 到直线CD 的距离为d ＝|k |1＋k 2＝21＋2＝63， 所以△OCD 的面积为S ＝12|CD |×d ＝12×332×63＝324.[解题师说]1．迁移要准(1)看到离心率的值想到e ＝ca ；看到垂直x 轴且过焦点的弦想到通径2b 2a ，联立求椭圆方程；看到向量的数量积想到设点．(2)过点F 且斜率为k 的直线与椭圆交于C ，D 两点⇒设点、直线方程与椭圆方程联立⇒消元，利用根与系数的关系⇒点的坐标，代入已知量⇒求出直线斜率⇒弦CD 的长、O 到弦CD 的距离⇒三角形的面积．2．方法要熟设而不求法求解直线与椭圆相交的弦长问题“设而不求”就是指在解题过程中根据需要设出变量，但并不直接求出其具体值，而是利用某种关系(如和、差、积)来表示变量之间的关系，最终通过等量代换，实现化简消元，在解决圆锥曲线的有关问题时能够达到一种“化难为易、化繁为简”的效果．步骤如下：(1)设直线Ax ＋By ＋C ＝0与椭圆mx 2＋ny 2＝1(m >0，n >0，m ≠n )的两个交点坐标分别为E (x 1，y 1)，F (x 2，y 2)；(2)把直线方程与椭圆方程联立方程组，消元得到一个一元二次方程； (3)利用根与系数的关系，得到x 1＋x 2与x 1x 2或y 1y 2与y 1＋y 2；(4)把与E ，F 有关要求的量(如弦长|EF |、直线与椭圆相关的图形面积等)用E ，F 的坐标表示出来，并变形为只含x 1＋x 2与x 1x 2(或y 1＋y 2与y 1y 2)的形式；(5)将(3)中所得的含有参数的式子等量代入(4)中，得到含参数的代数式，经过其他运算得到化简结果．3．结论要记(1)椭圆中最短的焦点弦为通径，长度为2b 2a.(2)设斜率为k (k ≠0)的直线l 与椭圆C 相交于A ，B 两点，A (x 1，y 1)，B (x 2，y 2)，则|AB |＝1＋k 2|x 1－x 2|＝1＋k 2·(x 1＋x 2)2－4x 1x 2或|AB |＝1＋1k2·|y 1－y 2|＝ 1＋1k 2·(y 1＋y 2)2－4y 1y 2.[冲关演练](2018·贵州适应性考试)设F 1，F 2分别是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，E 的离心率为22，点(0,1)是E 上一点． (1)求椭圆E 的方程；(2)过点F 1的直线交椭圆E 于A ，B 两点，且BF 1―→＝2F 1A ―→，求直线BF 2的方程．解：(1)由题意知，b ＝1，且e 2＝c 2a 2＝a 2－b 2a 2＝12，解得a 2＝2，所以椭圆E 的方程为x 22＋y 2＝1.(2)由题意知，直线AB 的斜率存在且不为0，故可设直线AB 的方程为x ＝my －1，设A (x 1，y 1)，B (x 2，y 2)．由⎩⎪⎨⎪⎧x 22＋y 2＝1，x ＝my －1得(m 2＋2)y 2－2my －1＝0， 则y 1＋y 2＝2mm 2＋2，① y 1y 2＝－1m 2＋2，② 因为F 1(－1,0)，所以BF 1―→＝(－1－x 2，－y 2)，F 1A ―→＝(x 1＋1，y 1)， 由BF 1―→＝2F 1A ―→可得，－y 2＝2y 1，③ 由①②③可得B ⎝⎛⎭⎫－12，±144，则kBF 2＝146或－146， 所以直线BF 2的方程为 y ＝146x －146或y ＝－146x ＋146.(一)普通高中适用作业A 级——基础小题练熟练快1．(2017·浙江高考)椭圆x 29＋y 24＝1的离心率是( )A.133B.53C.23D.59解析：选B 根据题意知，a ＝3，b ＝2，则c ＝a 2－b 2＝5，∴椭圆的离心率e ＝ca ＝53. 2．(2018·长沙模拟)椭圆E 的焦点在x 轴上，中心在原点，其短轴上的两个顶点和两个焦点恰为边长是2的正方形的顶点，则椭圆E 的标准方程为( )A.x 22＋y 22＝1 B.x 22＋y 2＝1C.x 24＋y 22＝1 D.y 24＋x 22＝1解析：选C 易知b ＝c ＝2，故a 2＝b 2＋c 2＝4，从而椭圆E 的标准方程为x 24＋y 22＝1.3．椭圆x 2m ＋y 24＝1的焦距为2，则m 的值是( )A ．6或2B ．5C ．1或9D ．3或5解析：选D 由题意，得c ＝1，当椭圆的焦点在x 轴上时，由m －4＝1，解得m ＝5；当椭圆的焦点在y 轴上时，由4－m ＝1，解得m ＝3，所以m 的值是3或5，故选D.4．设椭圆x 24＋y 23＝1的焦点为F 1，F 2，点P 在椭圆上，若△PF 1F 2是直角三角形，则△PF 1F 2的面积为( )A ．3B ．3或32C.32D ．6或3解析：选C 由已知a ＝2，b ＝3，c ＝1，则点P 为短轴顶点(0，3)时，∠F 1PF 2＝π3，△PF 1F 2是正三角形，若△PF 1F 2是直角三角形，则直角顶点不可能是点P ，只能是焦点F 1(或F 2)为直角顶点，此时|PF 1|＝b 2a ＝32⎝⎛⎭⎫或|PF 2|＝b 2a ，S △PF 1F 2＝12·b 2a ·2c ＝b 2c a ＝32.5．过椭圆x 25＋y 24＝1的右焦点作一条斜率为2的直线与椭圆交于A ，B 两点，O 为坐标原点，则△OAB 的面积为( )A.43B.53C.54D.103解析：选B 由题意知椭圆的右焦点F 的坐标为(1,0)，则直线AB 的方程为y ＝2x －2.联立⎩⎪⎨⎪⎧x 25＋y 24＝1，y ＝2x －2，解得交点(0，－2)，⎝⎛⎭⎫53，43，∴S △OAB ＝12·|OF |·|y A －y B |＝12×1×⎪⎪⎪⎪－2－43＝53，故选B. 6．设P 是椭圆x 225＋y 29＝1上一点，M ，N 分别是两圆：(x ＋4)2＋y 2＝1和(x －4)2＋y 2＝1上的点，则|PM |＋|PN |的最小值、最大值分别为( )A ．9,12B ．8,11C ．8,12D ．10,12解析：选C 如图所示，因为两个圆心恰好是椭圆的焦点，由椭圆的定义可知|PF 1|＋|PF 2|＝10，易知|PM |＋|PN |＝(|PM |＋|MF 1|)＋(|PN |＋|NF 2|)－2，则其最小值为|PF 1|＋|PF 2|－2＝8，最大值为|PF 1|＋|PF 2|＋2＝12.7．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，以原点为圆心，椭圆的短半轴长为半径的圆与直线x －y ＋6＝0相切，则椭圆C 的方程为________________．解析：由题意知e ＝c a ＝12，所以e 2＝c 2a 2＝a 2－b 2a 2＝14，即a 2＝43b 2.以原点为圆心，椭圆的短半轴长为半径的圆的方程为x 2＋y 2＝b 2，由题意可知b ＝62＝3，所以a 2＝4，b 2＝3.故椭圆C 的方程为x 24＋y 23＝1.答案：x 24＋y 23＝18．若F 1，F 2分别是椭圆E ：x 2＋y 2b2＝1(0<b <1)的左、右焦点，过点F 1的直线交椭圆E于A ，B 两点．若|AF 1|＝3|F 1B |，AF 2⊥x 轴，则椭圆E 的方程为________________．解析：设点A 在点B 上方，F 1(－c,0)，F 2(c,0)，其中c ＝1－b 2，则可设A (c ，b 2)，B (x 0，y 0)，由|AF 1|＝3|F 1B |，可得AF 1―→＝3F 1B ―→，故⎩⎪⎨⎪⎧－2c ＝3(x 0＋c )，－b 2＝3y 0，即⎩⎨⎧x 0＝－53c ，y 0＝－13b 2，代入椭圆方程可得25(1－b 2)9＋19b 2＝1，解得b 2＝23，故椭圆方程为x 2＋3y 22＝1.答案：x 2＋3y 22＝19．已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的一个焦点是圆x 2＋y 2－6x ＋8＝0的圆心，且短轴长为8，则椭圆的左顶点为______．解析：∵圆的标准方程为(x －3)2＋y 2＝1，∴圆心坐标为(3,0)，∴c ＝3.又b ＝4，∴a ＝b 2＋c 2＝5. ∵椭圆的焦点在x 轴上，∴椭圆的左顶点为(－5,0)． 答案：(－5,0)10．已知椭圆方程为x 2a 2＋y 2b 2＝1(a >b >0)，A ，B 分别是椭圆长轴的两个端点，M ，N 是椭圆上关于x 轴对称的两点，直线AM ，BN 的斜率分别为k 1，k 2，若|k 1·k 2|＝14，则椭圆的离心率为________．解析：设M (x 0，y 0)，则N (x 0，－y 0)，|k 1·k 2|＝⎪⎪⎪⎪y 0x 0＋a ·y 0a －x 0＝y 2a 2－x 20＝b 2⎝⎛⎭⎫1－x 2a 2a 2－x 20＝b2a 2＝14， 从而e ＝ 1－b 2a 2＝32. 答案：32B 级——中档题目练通抓牢1.如图，已知椭圆C 的中心为原点O ，F (－25，0)为C 的左焦点，P 为C 上一点，满足|OP |＝|OF |，且|PF |＝4，则椭圆C 的方程为( )A.x 225＋y 25＝1 B.x 236＋y 216＝1C.x 230＋y 210＝1 D.x 245＋y 225＝1解析：选B 设椭圆的标准方程为x 2a 2＋y 2b 2＝1(a >b >0)，焦距为2c ，右焦点为F ′，连接PF ′，如图所示．因为F (－25，0)为C 的左焦点，所以c ＝2 5.由|OP |＝|OF |＝|OF ′|知，∠FPF ′＝90°，即FP ⊥PF ′.在Rt △PFF ′中，由勾股定理，得|PF ′|＝|FF ′|2－|PF |2＝(45)2－42＝8.由椭圆定义，得|PF |＋|PF ′|＝2a ＝4＋8＝12，所以a ＝6，a 2＝36，于是b 2＝a 2－c 2＝36－(25)2＝16，所以椭圆C 的方程为x 236＋y 216＝1.2．已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右焦点为F ，短轴的一个端点为M ，直线l ：3x－4y ＝0交椭圆E 于A ，B 两点．若|AF |＋|BF |＝4，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值范围是( )A.⎝⎛⎦⎤0，32B.⎝⎛⎦⎤0，34C.⎣⎡⎭⎫32，1D.⎣⎡⎭⎫34，1解析：选A 根据椭圆的对称性及椭圆的定义可得A ，B 两点到椭圆左、右焦点的距离和为4a ＝2(|AF |＋|BF |)＝8，所以a ＝2.又d ＝|3×0－4×b |32＋(－4)2≥45，所以1≤b ＜2，所以e ＝c a ＝ 1－b 2a2＝ 1－b 24.因为1≤b ＜2，所以0＜e ≤32.3．已知点P 是椭圆x 216＋y 28＝1上的动点，F 1，F 2分别是椭圆的左、右焦点，O 是坐标原点，若M 是∠F 1PF 2的平分线上一点，且F 1M ―→·MP ―→＝0，则|OM ―→|的取值范围是( )A ．[0,3)B ．(0,22)C ．[22，3)D ．(0,4]解析：选B 如图，延长F 1M 交PF 2的延长线于点G . ∵F 1M ―→·MP ―→＝0，∴F 1M ―→⊥MP ―→. 又MP 为∠F 1PF 2的平分线， ∴|PF 1|＝|PG |，且M 为F 1G 的中点． ∵O 为F 1F 2中点，∴OM 綊12F 2G .∵|F 2G |＝||PF 2|－|PG ||＝||PF 1|－|PF 2||， ∴|OM ―→|＝12|2a －2|PF 2||＝|4－|PF 2||.∵4－22<|PF 2|<4或4<|PF 2|<4＋22， ∴|OM ―→|∈(0,22)．4．(2018·广东五校协作体第一次诊断考试)已知椭圆C ：x 22＋y 2＝1的两焦点为F 1，F 2，点P (x 0，y 0)满足0＜x 202＋y 20＜1，则|PF 1|＋|PF 2|的取值范围是________． 解析：由点P (x 0，y 0)满足0＜x 22＋y 20＜1，可知P (x 0，y 0)一定在椭圆内(不包括原点)，因为a ＝2，b ＝1，所以由椭圆的定义可知|PF 1|＋|PF 2|＜2a ＝22，当P (x 0，y 0)与F 1或F 2重合时，|PF 1|＋|PF 2|＝2，又|PF 1|＋|PF 2|≥|F 1F 2|＝2，故|PF 1|＋|PF 2|的取值范围是[2,22)．答案：[2,22)5.如图，椭圆的中心在坐标原点O ，顶点分别是A 1，A 2，B 1，B 2，焦点分别为F 1，F 2，延长B 1F 2与A 2B 2交于P 点，若∠B 1PA 2为钝角，则此椭圆的离心率的取值范围为________．解析：设椭圆的方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，∠B 1PA 2为钝角可转化为B 2A 2―→，F 2B 1―→所夹的角为钝角，则(a ，－b )·(－c ，－b )＜0，即b 2＜ac ，则a 2－c 2＜ac ，故⎝⎛⎭⎫c a 2＋ca －1＞0，即e 2＋e －1＞0，解得e ＞5－12或e ＜－5－12，又0＜e ＜1，所以5－12＜e ＜1. 答案：⎝⎛⎭⎪⎫5－12，1 6．已知椭圆G ：x 2a 2＋y 2b 2＝1(a >b >0)在y 轴上的一个顶点为M ，两个焦点分别是F 1，F 2，∠F 1MF 2＝120°，△MF 1F 2的面积为 3.(1)求椭圆G 的方程；(2)过椭圆G 长轴上的点P (t,0)的直线l 与圆O ：x 2＋y 2＝1相切于点Q (Q 与P 不重合)，交椭圆G 于A ，B 两点．若|AQ |＝|BP |，求实数t 的值．解：(1)由椭圆性质，知|MF 2|＝a ， 于是c ＝a sin 60°＝32a ，b ＝a cos 60°＝12a . 所以△MF 1F 2的面积S ＝12·(2c )·b ＝12·(3a )·⎝⎛⎭⎫12a ＝3，解得a ＝2，b ＝1. 所以椭圆G 的方程为x 24＋y 2＝1.(2)显然，直线l 与y 轴不平行，可设其方程为y ＝k (x －t )． 由于直线l 与圆O 相切， 则圆心O 到l 的距离d ＝|kt |k 2＋1＝1， 即k 2t 2＝k 2＋1， ①联立⎩⎪⎨⎪⎧x 2＋4y 2＝4，y ＝k (x －t )，化简得(1＋4k 2)x 2－8tk 2x ＋4(t 2k 2－1)＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝8tk 21＋4k 2.设Q (x 0，y 0)，有⎩⎪⎨⎪⎧y 0＝k (x 0－t )，y 0x 0＝－1k ，解得x 0＝tk 21＋k 2. 由已知可得，线段AB ，PQ 中点重合，即有x 1＋x 2＝t ＋x 0. 因此8tk 21＋4k 2＝t ＋tk 21＋k 2，化简得k 2＝12， 将其代入①式，可得t ＝±3.7．(2018·成都一诊)已知椭圆x 25＋y 24＝1的右焦点为F ，设直线l ：x ＝5与x 轴的交点为E ，过点F 且斜率为k 的直线l 1与椭圆交于A ，B 两点，M 为线段EF 的中点．(1)若直线l 1的倾斜角为π4，求|AB |的值；(2)设直线AM 交直线l 于点N ，证明：直线BN ⊥l . 解：由题意知，F (1,0)，E (5,0)，M (3,0)． (1)∵直线l 1的倾斜角为π4，∴斜率k ＝1.∴直线l 1的方程为y ＝x －1.代入椭圆方程，可得9x 2－10x －15＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝109，x 1x 2＝－53. ∴|AB |＝2·(x 1＋x 2)2－4x 1x 2 ＝2×⎝⎛⎭⎫1092＋4×53＝1659.(2)证明：设直线l 1的方程为y ＝k (x －1)． 代入椭圆方程，得(4＋5k 2)x 2－10k 2x ＋5k 2－20＝0. 设A (x 1，y 1)，B (x 2，y 2)， 则x 1＋x 2＝10k 24＋5k 2，x 1x 2＝5k 2－204＋5k 2.设N (5，y 0)，∵A ，M ，N 三点共线， ∴－y 13－x 1＝y 02，∴y 0＝2y 1x 1－3. 而y 0－y 2＝2y 1x 1－3－y 2＝2k (x 1－1)x 1－3－k (x 2－1) ＝3k (x 1＋x 2)－kx 1x 2－5kx 1－3＝3k ·10k 24＋5k 2－k ·5k 2－204＋5k 2－5k x 1－3＝0.∴直线BN ∥x 轴，即BN ⊥l .C 级——重难题目自主选做1．已知椭圆x 2a 2＋y 2b2＝1(a >b >0)，A ，B 为椭圆上的两点，线段AB 的垂直平分线交x 轴于点M ⎝⎛⎭⎫a 5，0，则椭圆的离心率e 的取值范围是( )A.⎝⎛⎭⎫22，1B.⎝⎛⎭⎫33，1C.⎝⎛⎭⎫55，1 D.⎝⎛⎭⎫34，1 解析：选C 设A (x 1，y 1)，B (x 2，y 2)，x 1≠x 2，则⎩⎪⎨⎪⎧ ⎝⎛⎭⎫x 1－a 52＋y 21＝⎝⎛⎭⎫x 2－a 52＋y 22，x 21a 2＋y21b 2＝1，x 22a 2＋y 22b 2＝1，即⎩⎪⎨⎪⎧2a 5(x 1－x 2)＝x 21－x 22＋y 21－y 22，y 21＝b 2－b2a 2x 21，y 22＝b 2－b 2a2x 22，所以2a5(x 1－x 2)＝a 2－b 2a 2(x 21－x 22)，所以2a 35(a 2－b 2)＝x 1＋x 2.又－a ≤x 1≤a ，－a ≤x 2≤a ，x 1≠x 2， 所以－2a <x 1＋x 2<2a ， 则2a 35(a 2－b 2)<2a ， 即b 2a 2<45，所以e 2＝1－b 2a 2>15. 又0<e <1，所以55<e <1. 2．已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1(－1，0)，F 2(1,0)，点A ⎝⎛⎭⎫1，22在椭圆C 上．(1)求椭圆C 的标准方程；(2)是否存在斜率为2的直线，使得当直线与椭圆C 有两个不同交点M ，N 时，能在直线y ＝53上找到一点P ，在椭圆C 上找到一点Q ，满足PM ―→＝NQ ―→？若存在，求出直线的方程；若不存在，说明理由．解：(1)设椭圆C 的焦距为2c ，则c ＝1，因为A ⎝⎛⎭⎫1，22在椭圆C 上， 所以2a ＝|AF 1|＋|AF 2|＝22， 因此a ＝2，b 2＝a 2－c 2＝1， 故椭圆C 的方程为x 22＋y 2＝1.(2)不存在满足条件的直线，证明如下：设直线的方程为y ＝2x ＋t ，M (x 1，y 1)，N (x 2，y 2)， P ⎝⎛⎭⎫x 3，53，Q (x 4，y 4)，MN 的中点为D (x 0，y 0)， 由⎩⎪⎨⎪⎧y ＝2x ＋t ，x 22＋y 2＝1消去x ，得9y 2－2ty ＋t 2－8＝0， 所以y 1＋y 2＝2t9，且Δ＝4t 2－36(t 2－8)＞0，故y 0＝y 1＋y 22＝t9，且－3＜t ＜3. 由PM ―→＝NQ ―→，得⎝⎛⎭⎫x 1－x 3，y 1－53＝(x 4－x 2，y 4－y 2)， 所以有y 1－53＝y 4－y 2，y 4＝y 1＋y 2－53＝2t 9－53.也可由PM ―→＝NQ ―→知四边形PMQN 为平行四边形， 而D 为线段MN 的中点，因此，D 也为线段PQ 的中点， 所以y 0＝53＋y 42＝t 9，可得y 4＝2t －159又－3＜t ＜3，所以－73＜y 4＜－1，与椭圆上点的纵坐标的取值范围是[－1,1]矛盾． 因此不存在满足条件的直线．(二)重点高中适用作业A 级——保分题目巧做快做1．在平面直角坐标系xOy 中，P 是椭圆y 24＋x 23＝1上的一个动点，点A (1,1)，B (0，－1)，则|PA |＋|PB |的最大值为( )A ．2B ．3C ．4D ．5解析：选D ∵椭圆方程为y 24＋x 23＝1，∴焦点坐标为B (0，－1)和B ′(0,1)， 连接PB ′，AB ′，根据椭圆的定义， 得|PB |＋|PB ′|＝2a ＝4， 可得|PB |＝4－|PB ′|，因此|PA |＋|PB |＝|PA |＋(4－|PB ′|) ＝4＋(|PA |－|PB ′|)． ∵|PA |－|PB ′|≤|AB ′|，∴|PA |＋|PB |≤4＋|AB ′|＝4＋1＝5.当且仅当点P 在AB ′延长线上时，等号成立． 综上所述，可得|PA |＋|PB |的最大值为5.2．已知椭圆C ：x 24＋y 23＝1的左、右焦点分别为F 1，F 2，椭圆C 上的点A 满足AF 2⊥F 1F 2，若点P 是椭圆C 上的动点，则F 1P ―→·F 2A ―→的最大值为( )A.32B.332C.94D.154解析：选B 由椭圆方程知c ＝1， 所以F 1(－1,0)，F 2(1,0)．因为椭圆C 上的点A 满足AF 2⊥F 1F 2，则可设A (1，y 0)， 代入椭圆方程可得y 20＝94，所以y 0＝±32.设P (x 1，y 1)，则F 1P ―→＝(x 1＋1，y 1)，F 2A ―→＝(0，y 0)， 所以F 1P ―→·F 2A ―→＝y 1y 0.因为点P 是椭圆C 上的动点，所以－3≤y 1≤3， 故F 1P ―→·F 2A ―→的最大值为332.3．已知椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的右焦点为F (3,0)，过点F 的直线交E 于A ，B 两点．若AB 的中点坐标为(1，－1)，则椭圆E 的方程为( )A.x 245＋y 236＝1 B.x 236＋y 227＝1C.x 227＋y 218＝1 D.x 218＋y 29＝1解析：选D 因为直线AB 过点F (3,0)和点(1，－1)，所以直线AB 的方程为y ＝12(x －3)，代入椭圆方程x 2a 2＋y 2b 2＝1消去y ，得⎝⎛⎭⎫a 24＋b 2x 2－32a 2x ＋94a 2－a 2b 2＝0，所以AB 的中点的横坐标为32a 22⎝⎛⎭⎫a24＋b 2＝1，即a 2＝2b 2，又a 2＝b 2＋c 2，所以b 2＝9，a 2＝18，即椭圆E 的方程为x 218＋y 29＝1. 4．如果椭圆x 236＋y 29＝1的弦AB 被点M (x 0，y 0)平分，设直线AB 的斜率为k 1，直线OM (O为坐标原点)的斜率为k 2，则k 1k 2的值为( )A ．4 B.14C ．－1D ．－14解析：选D 设直线AB 的方程为y ＝k 1x ＋b ，A (x 1，y 1)，B (x 2，y 2)．代入椭圆方程并整理得，(1＋4k 21)x 2＋8k 1bx ＋4b 2－36＝0，x 1＋x 2＝－8k 1b 1＋4k 21，又中点M (x 0，y 0)在直线AB 上，所以y 1＋y 22＝k 1⎝⎛⎭⎫x 1＋x 22＋b ＝b 1＋4k 21，从而得弦中点M 的坐标为⎝⎛⎭⎫－4k 1b 1＋4k 21，b 1＋4k 21，∴k 2＝b 1＋4k 21－4k 1b 1＋4k 21＝－14k 1，∴k 1k 2＝－14.5．已知两定点A (－2,0)和B (2,0)，动点P (x ，y )在直线l ：y ＝x ＋3上移动，椭圆C 以A ，B 为焦点且经过点P ，则椭圆C 的离心率的最大值为( )A.2613B.22613C.21313D.41313解析：选B 设点A 关于直线l 的对称点为A 1(x 1，y 1)，则有⎩⎨⎧y 1x 1＋2＝－1，y 12＝x 1－22＋3，解得x 1＝－3，y 1＝1，则A 1(－3,1)，易知|PA |＋|PB |的最小值等于|A 1B |＝26，因此椭圆C 的离心率e ＝|AB ||PA |＋|PB |＝4|PA |＋|PB |的最大值为22613.6．(2018·广东五校协作体第一次诊断考试)已知椭圆C ：x 22＋y 2＝1的两焦点为F 1，F 2，点P (x 0，y 0)满足0＜x 202＋y 20＜1，则|PF 1|＋|PF 2|的取值范围是________． 解析：由点P (x 0，y 0)满足0＜x 22＋y 20＜1，可知P (x 0，y 0)一定在椭圆内(不包括原点)，因为a ＝2，b ＝1，所以由椭圆的定义可知|PF 1|＋|PF 2|＜2a ＝22，当P (x 0，y 0)与F 1或F 2重合时，|PF 1|＋|PF 2|＝2，又|PF 1|＋|PF 2|≥|F 1F 2|＝2，故|PF 1|＋|PF 2|的取值范围是[2,22)．答案：[2,22)7．已知M (x 0，y 0)是椭圆E ：x 2a 2＋y 2b2＝1(a >b >0)上一点，A ，B 是其左、右顶点，若2AM ―→·BM―→＝x 20－a 2，则离心率e ＝________.解析：由题意知A (－a,0)，B (a,0)，∴AM ―→＝(x 0＋a ，y 0)，BM ―→＝(x 0－a ，y 0)，∵2AM ―→·BM―→＝x 20－a 2，∴2(x 20－a 2＋y 20)＝x 20－a 2，∴x 20＝a 2－2y 20. 又x 20a 2＋y 20b 2＝1，∴a 2－2y 20a 2＋y 20b2＝1， ∴－2a 2＋1b2＝0，∴a 2＝2b 2，∴c 2a 2＝a 2－b 2a 2＝1－b 2a 2＝1－12＝12，∴e ＝22. 答案：228．(2018·湖南东部六校联考)设P ，Q 分别是圆x 2＋(y －1)2＝3和椭圆x 24＋y 2＝1上的点，则P ，Q 两点间的最大距离是________．解析：依据圆的性质可知，P ，Q 两点间的最大距离可以转化为圆心到椭圆上点的距离的最大值加上圆的半径3，设Q (x ，y )，则圆心(0,1)到椭圆上点的距离为 d ＝x 2＋(y －1)2＝－3y 2－2y ＋5 ＝－3⎝⎛⎭⎫y ＋132＋163， ∵－1≤y ≤1，∴当y ＝－13时，d 取最大值433，所以P ，Q 两点间的最大距离为433＋3＝733. 答案：7339．已知椭圆G ：x 2a 2＋y 2b 2＝1(a >b >0)在y 轴上的一个顶点为M ，两个焦点分别是F 1，F 2，∠F 1MF 2＝120°，△MF 1F 2的面积为 3.(1)求椭圆G 的方程；(2)过椭圆G 长轴上的点P (t,0)的直线l 与圆O ：x 2＋y 2＝1相切于点Q (Q 与P 不重合)，交椭圆G 于A ，B 两点．若|AQ |＝|BP |，求实数t 的值．解：(1)由椭圆性质，知|MF 2|＝a ， 于是c ＝a sin 60°＝32a ，b ＝a cos 60°＝12a . 所以△MF 1F 2的面积S ＝12·(2c )·b ＝12·(3a )·⎝⎛⎭⎫12a ＝3，解得a ＝2，b ＝1. 所以椭圆G 的方程为x 24＋y 2＝1.(2)显然，直线l 与y 轴不平行，可设其方程为y ＝k (x －t )． 由于直线l 与圆O 相切， 则圆心O 到l 的距离d ＝|kt |k 2＋1＝1， 即k 2t 2＝k 2＋1， ①联立⎩⎪⎨⎪⎧x 2＋4y 2＝4，y ＝k (x －t )，化简得(1＋4k 2)x 2－8tk 2x ＋4(t 2k 2－1)＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝8tk 21＋4k 2.设Q (x 0，y 0)，有⎩⎪⎨⎪⎧y 0＝k (x 0－t )，y 0x 0＝－1k ，解得x 0＝tk 21＋k 2. 由已知可得，线段AB ，PQ 中点重合，即有x 1＋x 2＝t ＋x 0. 因此8tk 21＋4k 2＝t ＋tk 21＋k 2，化简得k 2＝12， 将其代入①式，可得t ＝±3.10．(2018·成都一诊)已知椭圆x 25＋y 24＝1的右焦点为F ，设直线l ：x ＝5与x 轴的交点为E ，过点F 且斜率为k 的直线l 1与椭圆交于A ，B 两点，M 为线段EF 的中点．(1)若直线l 1的倾斜角为π4，求|AB |的值；(2)设直线AM 交直线l 于点N ，证明：直线BN ⊥l . 解：由题意知，F (1,0)，E (5,0)，M (3,0)． (1)∵直线l 1的倾斜角为π4，∴斜率k ＝1.∴直线l 1的方程为y ＝x －1.代入椭圆方程，可得9x 2－10x －15＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝109，x 1x 2＝－53. ∴|AB |＝2·(x 1＋x 2)2－4x 1x 2 ＝2×⎝⎛⎭⎫1092＋4×53＝1659.(2)证明：设直线l 1的方程为y ＝k (x －1)． 代入椭圆方程，得(4＋5k 2)x 2－10k 2x ＋5k 2－20＝0. 设A (x 1，y 1)，B (x 2，y 2)， 则x 1＋x 2＝10k 24＋5k 2，x 1x 2＝5k 2－204＋5k 2.设N (5，y 0)，∵A ，M ，N 三点共线， ∴－y 13－x 1＝y 02，∴y 0＝2y 1x 1－3. 而y 0－y 2＝2y 1x 1－3－y 2＝2k (x 1－1)x 1－3－k (x 2－1) ＝3k (x 1＋x 2)－kx 1x 2－5kx 1－3＝3k ·10k 24＋5k 2－k ·5k 2－204＋5k 2－5k x 1－3＝0.∴直线BN ∥x 轴，即BN ⊥l .B 级——拔高题目稳做准做1．已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，且|F 1F 2|＝2c ，若椭圆上存在点M 使得sin ∠MF 1F 2a ＝sin ∠MF 2F 1c，则该椭圆离心率的取值范围为( ) A ．(0，2－1)B.⎝⎛⎭⎫22，1C.⎝⎛⎭⎫0，22 D ．(2－1,1) 解析：选D 在△MF 1F 2中，|MF 2|sin ∠MF 1F 2＝|MF 1|sin ∠MF 2F 1，而sin ∠MF 1F 2a ＝sin ∠MF 2F 1c ， ∴|MF 2||MF 1|＝sin ∠MF 1F 2sin ∠MF 2F 1＝a c.① 又M 是椭圆x 2a 2＋y 2b 2＝1上一点，F 1，F 2是椭圆的焦点，∴|MF 1|＋|MF 2|＝2a .②由①②得，|MF 1|＝2ac a ＋c ，|MF 2|＝2a 2a ＋c .显然|MF 2|>|MF 1|，∴a －c <|MF 2|<a ＋c ，即a －c <2a 2a ＋c <a ＋c ，整理得c 2＋2ac －a 2>0，∴e 2＋2e －1>0，又0<e <1， ∴2－1<e <1，故选D.2.如图，圆O 与离心率为32的椭圆T ：x 2a 2＋y 2b 2＝1(a >b >0)相切于点M (0,1)，过点M 引两条互相垂直的直线l 1，l 2，两直线与两曲线分别交于点A ，C 与点B ，D (均不重合)．若P 为椭圆上任一点，记点P 到两直线的距离分别为d 1，d 2，则d 21＋d 22的最大值是( )A ．4B ．5 C.163D.253解析：选C 易知椭圆C 的方程为x 24＋y 2＝1，圆O 的方程为x 2＋y 2＝1，设P (x 0，y 0)，因为l 1⊥l 2，则d 21＋d 22＝|PM |2＝x 20＋(y 0－1)2，因为x 204＋y 20＝1，所以d 21＋d 22＝4－4y 20＋(y 0－1)2＝－3⎝⎛⎭⎫y 0＋132＋163，因为－1≤y 0≤1，所以当y 0＝－13时，d 21＋d 22取得最大值163. 3．设F 是椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的一个焦点，P 是C 上的点，圆x 2＋y 2＝a 29与线段PF 交于A ，B 两点，若A ，B 是线段PF 的两个三等分点，则椭圆C 的离心率为( )A.33 B.53 C.104D.175解析：选D 如图所示，设线段AB 的中点为D ，连接OD ，OA ，设椭圆C 的左、右焦点分别为F ，F 1，连接PF 1.设|OD |＝t ，因为点A ，B 是线段PF 的两个三等分点，所以点D 为线段PF 的中点，所以OD ∥PF 1，且|PF 1|＝2t ，PF 1⊥PF .因为|PF |＝3|AB |＝6|AD |＝6 ⎝⎛⎭⎫a 32－t 2，根据椭圆的定义，得|PF |＋|PF 1|＝2a ，∴6⎝⎛⎭⎫a 32－t 2＋2t ＝2a ，解得t ＝a 5或t ＝0(舍去)．所以|PF |＝8a 5，|PF 1|＝2a5.在Rt △PFF 1中，|PF |2＋|PF 1|2＝|FF 1|2，即⎝⎛⎭⎫8a 52＋⎝⎛⎭⎫2a 52＝(2c )2，得c 2a 2＝1725，所以椭圆C 的离心率e ＝c a ＝175.4.如图，在平面直角坐标系xOy 中，F 是椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右焦点，直线y ＝b2与椭圆交于B ，C 两点，且∠BFC ＝90°，则该椭圆的离心率是________．解析：将y ＝b 2代入椭圆的标准方程，得x 2a 2＋b 24b 2＝1，所以x ＝±32a ，故B ⎝⎛⎭⎫－32a ，b 2，C⎝⎛⎭⎫32a ，b 2.又因为F (c,0)，所以BF ―→＝⎝⎛⎭⎫c ＋32a ，－b 2，CF ―→＝⎝⎛⎭⎫c －32a ，－b 2.因为∠BFC ＝90°，所以BF ―→·CF ―→＝0， 所以⎝⎛⎭⎫c ＋32a ⎝⎛⎭⎫c －32a ＋⎝⎛⎭⎫－b 22＝0， 即c 2－34a 2＋14b 2＝0，将b 2＝a 2－c 2代入并化简，得a 2＝32c 2，所以e 2＝c 2a 2＝23，所以e ＝63(负值舍去)．答案：635．(2018·云南统测)已知焦点在y 轴上的椭圆E 的中心是原点O ，离心率等于32，以椭圆E 的长轴和短轴为对角线的四边形的周长为4 5.直线l ：y ＝kx ＋m 与y 轴交于点P ，与椭圆E 相交于A ，B 两点．(1)求椭圆E 的方程；(2)若AP ―→AP ―→＝3PB ―→，求m 2的取值范围．解：(1)根据已知设椭圆E 的方程为y 2a 2＋x 2b 2＝1(a >b >0)，焦距为2c ，由已知得c a ＝32，∴c ＝32a ，b 2＝a 2－c 2＝a 24.∵以椭圆E 的长轴和短轴为对角线的四边形的周长为45， ∴4a 2＋b 2＝25a ＝45，∴a ＝2，b ＝1. ∴椭圆E 的方程为x 2＋y 24＝1.(2)根据已知得P (0，m )，设A (x 1，kx 1＋m )，B (x 2，kx 2＋m )，由⎩⎪⎨⎪⎧y ＝kx ＋m ，4x 2＋y 2－4＝0得，(k 2＋4)x 2＋2mkx ＋m 2－4＝0. 由已知得Δ＝4m 2k 2－4(k 2＋4)(m 2－4)>0， 即k 2－m 2＋4>0，且x 1＋x 2＝－2km k 2＋4，x 1x 2＝m 2－4k 2＋4.由AP ―→＝3PB ―→，得x 1＝－3x 2.∴3(x 1＋x 2)2＋4x 1x 2＝12x 22－12x 22＝0.∴12k 2m 2(k 2＋4)2＋4(m 2－4)k 2＋4＝0，即m 2k 2＋m 2－k 2－4＝0. 当m 2＝1时，m 2k 2＋m 2－k 2－4＝0不成立， ∴k 2＝4－m 2m 2－1.∵k 2－m 2＋4>0，∴4－m 2m 2－1－m 2＋4>0，即(4－m 2)m 2m 2－1>0. ∴1<m 2<4.∴m 2的取值范围为(1,4)．6．已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1(－1，0)，F 2(1,0)，点A ⎝⎛⎭⎫1，22在椭圆C 上．(1)求椭圆C 的标准方程；(2)是否存在斜率为2的直线，使得当直线与椭圆C 有两个不同交点M ，N 时，能在直线y ＝53上找到一点P ，在椭圆C 上找到一点Q ，满足PM ―→＝NQ ―→？若存在，求出直线的方程；若不存在，说明理由．解：(1)设椭圆C 的焦距为2c ，则c ＝1，因为A ⎝⎛⎭⎫1，22在椭圆C 上， 所以2a ＝|AF 1|＋|AF 2|＝22， 因此a ＝2，b 2＝a 2－c 2＝1， 故椭圆C 的方程为x 22＋y 2＝1.(2)不存在满足条件的直线，证明如下：设直线的方程为y ＝2x ＋t ，M (x 1，y 1)，N (x 2，y 2)，P ⎝⎛⎭⎫x 3，53，Q (x 4，y 4)，MN 的中点为D (x 0，y 0)，由⎩⎪⎨⎪⎧y ＝2x ＋t ，x 22＋y 2＝1消去x ，得9y 2－2ty ＋t 2－8＝0， 所以y 1＋y 2＝2t9，且Δ＝4t 2－36(t 2－8)＞0，故y 0＝y 1＋y 22＝t9，且－3＜t ＜3. 由PM ―→＝NQ ―→，得⎝⎛⎭⎫x 1－x 3，y 1－53＝(x 4－x 2，y 4－y 2)， 所以有y 1－53＝y 4－y 2，y 4＝y 1＋y 2－53＝2t 9－53.也可由PM ―→＝NQ ―→知四边形PMQN 为平行四边形， 而D 为线段MN 的中点，因此，D 也为线段PQ 的中点， 所以y 0＝53＋y 42＝t 9，可得y 4＝2t －159又－3＜t ＜3，所以－73＜y 4＜－1，与椭圆上点的纵坐标的取值范围是[－1,1]矛盾． 因此不存在满足条件的直线．。

2019届高考数学一轮复习第八章平面解析几何第五节椭圆课时作业编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2019届高考数学一轮复习第八章平面解析几何第五节椭圆课时作业）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2019届高考数学一轮复习第八章平面解析几何第五节椭圆课时作业的全部内容。

第五节 椭圆课时作业 A 组——基础对点练1．已知椭圆错误!＋错误!＝1（m >0)的左焦点为F 1（－4,0），则m ＝（ ) A ．2 B ．3 C ．4 D ．9 解析：由4＝25－m 2（m >0)⇒m ＝3,故选B 。

答案：B2．方程kx 2＋4y 2＝4k 表示焦点在x 轴上的椭圆，则实数k 的取值范围是( ） A ．k >4 B ．k ＝4 C ．k 〈4D ．0〈k 〈4解析:方程kx 2＋4y 2＝4k 表示焦点在x 轴上的椭圆，即方程错误!＋错误!＝1表示焦点在x 轴上的椭圆,可得0<k 〈4，故选D 。

答案:D3．已知椭圆的中心在原点，离心率e ＝错误!，且它的一个焦点与抛物线y 2＝－4x 的焦点重合，则此椭圆方程为( ） A.错误!＋错误!＝1 B ．错误!＋错误!＝1 C.错误!＋y 2＝1D ．错误!＋y 2＝1解析：依题意，可设椭圆的标准方程为x 2a2＋错误!＝1(a 〉b 〉0），由已知可得抛物线的焦点为(－1,0），所以c ＝1，又离心率e ＝错误!＝错误!,解得a ＝2，b 2＝a 2－c 2＝3，所以椭圆方程为错误!＋错误!＝1,故选A.答案：A4．椭圆错误!＋错误!＝1（a 〉b 〉0）的左、右顶点分别为A ，B ,左、右焦点分别为F 1，F 2，若｜AF 1|，｜F 1F 2｜，｜F 1B |成等差数列,则此椭圆的离心率为( ） A.错误! B ．错误! C 。

[备考方向要明了] 考 什 么怎 么 考1.掌握椭圆的定义、几何图形、标准方程及简单性质． 2.了解圆锥曲线的简单应用． 3.理解数形结合的思想.1.椭圆的定义、标准方程和几何性质是高考的重点考查内容，三种题型均有可能出现，如2012年山东T10等．2.直线与椭圆位置关系问题一直是高考的重点，多以解答题形式考查，难度相对较大，如2012年陕西T19等. [归纳·知识整合] 1．椭圆的定义 (1)满足以下条件的点的轨迹是椭圆 在平面内； 与两个定点F1、F2的距离之和等于常数； 常数大于|F1F2|. (2)焦点：两定点． (3)焦距：两焦点间的距离． [探究]　1.在椭圆的定义中，若2a＝|F1F2|或2a<|F1F2|，则动点的轨迹如何？ 提示：当2a＝|F1F2|时动点的轨迹是线段F1F2；当2ab>0)＋＝1(a>b>0)图形性质范围－a≤x≤a－b≤y≤b－b≤x≤b－a≤y≤a对称性对称轴：x轴、y轴对称中心：(0,0)顶点A1(－a,0)，A2(a,0)B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a) B1(－b,0)，B2(b,0)轴长轴A1A2的长为2a短轴B1B2的长为2b焦距|F1F2|＝2c离心率e＝，e(0,1)a，b，c的关系c2＝a2－b2 [探究]　2.椭圆离心率的大小与椭圆的扁平程度有怎样的关系？ 提示：离心率e＝越接近1，a与c就越接近，从而b＝就越小，椭圆就越扁平；同理离心率越接近0，椭圆就越接近于圆． [自测·牛刀小试] 1．椭圆＋＝1的离心率为( ) A. B. C. D. 解析：选D　a2＝16，b2＝8，c2＝8，e＝＝. 2．已知F1，F2是椭圆＋＝1的两焦点，过点F2的直线交椭圆于A，B两点，在AF1B中，若有两边之和是10，则第三边的长度为( ) A．6 B．5 C．4 D．3 解析：选A　根据椭圆定义，知AF1B的周长为4a＝16，故所求的第三边的长度为16－10＝6. 3．椭圆x2＋my2＝1的焦点在y轴上，长轴长是短轴长的两倍，则m的值为( ) A. B. C．2 D．4 解析：选A　由题意知a2＝，b2＝1，且a＝2b，则＝4，得m＝. 4．若椭圆＋＝1过点(－2，)，则其焦距为( ) A．2 B．2 C．4 D．4 解析：选C　把点(－2，)的坐标代入椭圆方程得m2＝4，所以c2＝16－4＝12，所以c＝2，故焦距为2c＝4. 5．设F1、F2分别是椭圆＋＝1的左、右焦点，P为椭圆上一点，M是F1P的中点，|OM|＝3，则P点到椭圆左焦点的距离为________． 解析：由题意知|OM|＝|PF2|＝3，则|PF2|＝6.故|PF1|＝2×5－6＝4. 答案：4 椭圆的定义、标准方程 [例1]　(1)已知ABC的顶点B、C在椭圆＋y2＝1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则ABC是周长是( ) A．2 B．6 C．4 D．12 (2)(2012·山东高考)已知椭圆C：＋＝1(a>b>0)的离心率为.双曲线x2－y2＝1的渐近线与椭圆C有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程为( )A.＋＝1B.＋＝1C.＋＝1D.＋＝1 [自主解答]　(1)根据椭圆定义，ABC的周长等于椭圆长轴长的2倍，即4. (2)由离心率为得，a2＝4b2，排除选项B，双曲线的渐近线方程为y＝±x，与椭圆的四交点组成的四边形的面积为16可得在第一象限的交点坐标为(2,2)，代入选项A、C、D，知选项D正确． [答案]　(1)C　(2)D ——————————————————— 用待定系数法求椭圆方程的一般步骤 (1)作判断：根据条件判断椭圆的焦点在x轴上，还是在y轴上，还是两个坐标轴都有可能； (2)设方程：根据上述判断设方程＋＝1(a>b>0)或＋＝1(a>b>0)； ?3?找关系：根据已知条件，建立关于a、b、c或m、n的方程组；?4?得方程：解方程组，将解代入所设方程，即为所求.注意：用待定系数法求椭圆的方程时，要“先定型，再定量”，不能确定焦点的位置时，可进行分类讨论或把椭圆的方程设为mx2＋ny2＝1?m>0，n>0?. 1．已知椭圆G的中心在坐标原点，长轴在x轴上，离心率为，且椭圆上一点到椭圆的两个焦点的距离之和为12，则椭圆G的方程为______________． 解析：设椭圆方程为＋＝1(a>b>0)，根据椭圆定义2a＝12，即a＝6，又＝，得c＝3，故b2＝a2－c2＝36－27＝9，故所求椭圆方程为＋＝1. 答案：＋＝1 2．已知F1，F2是椭圆C：＋＝1(a>b>0)的左、右焦点，P为椭圆C上一点，且12.若PF1F2的面积为9，则b＝________. 解析：设椭圆的焦点坐标为(±c,0)根据椭圆定义和PF1F2是一个面积等于9的直角三角形， 有 式两端平方并把、两式代入可得4c2＋36＝4a2， 即a2－c2＝9，即b2＝9，故b＝3. 答案：3 椭圆的几何性质及应用 [例2]　(2012·安徽高考)如图，F1，F2分别是椭圆C：＋＝1(a>b>0)的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，F1AF2＝60°. (1)求椭圆C的离心率； (2)已知AF1B的面积为40，求a，b的值． [自主解答]　(1)由题意可知，AF1F2为等边三角形，a＝2c，所以e＝. (2)法一：a2＝4c2，b2＝3c2， 直线AB的方程可为y＝－(x－c)． 将其代入椭圆方程3x2＋4y2＝12c2，得B. 所以|AB|＝·＝c. 由SAF1B＝|AF1|·|AB|sin F1AB＝a·c·＝a2＝40，解得a＝10，b＝5. 法二：设|AB|＝t. 因为|AF2|＝a，所以|BF2|＝t－a. 由椭圆定义|BF1|＋|BF2|＝2a可知，|BF1|＝3a－t. 再由余弦定理(3a－t)2＝a2＋t2－2atcos 60°可得， t＝a. 由S△AF1B＝a·a·＝a2＝40知， a＝10，b＝5. ——————————————————— 椭圆离心率的求法 求椭圆的离心率(或范围)时，一般是依据题设得出一个关于a，b，c的等式(或不等式)，利用a2＝b2＋c2消去b，即可求得离心率或离心率的范围． 3．椭圆＋＝1(a>b>0)的两顶点为A(a,0)，B(0，b)，且左焦点为F，FAB是以角B为直角的直角三角形，则椭圆的离心率e为( ) A. B. C. D. 解析：选B　根据已知a2＋b2＋a2＝(a＋c)2，即c2＋ac－a2＝0，即e2＋e－1＝0，解得e＝，故所求的椭圆的离心率为. 4．椭圆＋＝1(a为定值，且a>)的左焦点为F，直线x＝m与椭圆相交于点A，B，FAB的周长的最大值是12，则该椭圆的离心率是________． 解析：设椭圆右焦点为F′，由图及椭圆定义知，|AF|＋|AF′|＝|BF|＋|BF′|＝2a. 又FAB的周长为|AF|＋|BF|＋|AB|≤|AF|＋|BF|＋|AF′|＋|BF′|＝4a，当且仅当AB过右焦点F′时等号成立，此时4a＝12，则a＝3，故椭圆方程为＋＝1, 所以c＝2，所以e＝＝. 答案： 直线与椭圆的综合 [例3]　如图，椭圆C：＋＝1(a＞b＞0)的离心率为，其左焦点到点P(2,1)的距离为.不过原点O的直线l与C相交于A，B两点，且线段AB被直线OP平分． (1)求椭圆C的方程； (2)求ABP面积取最大值时直线l的方程． [自主解答]　(1)设椭圆左焦点为F(－c,0)，则由题意得 解得 所以椭圆方程为＋＝1. (2)设A(x1，y1)，B(x2，y2)，线段AB的中点为M. 当直线AB与x轴垂直时，直线AB的方程为x＝0，与不过原点的条件不符，舍去．故可设直线AB的方程为y＝kx＋m(m≠0)， 由消去y，整理得 (3＋4k2)x2＋8kmx＋4m2－12＝0， 则Δ＝64k2m2－4(3＋4k2)(4m2－12)＞0， 所以线段AB的中点M. 因为M在直线OP：y＝x上，所以＝. 得m＝0(舍去)或k＝－. 此时方程为3x2－3mx＋m2－3＝0，则 Δ＝3(12－m2)＞0， 所以|AB|＝·|x1－x2|＝·. 设点P到直线AB距离为d，则 d＝＝. 设ABP的面积为S，则 S＝|AB|·d＝·. 其中m(－2，0)(0,2)． 令u(m)＝(12－m2)(m－4)2，m[－2，2 ]， u′(m)＝－4(m－4)(m2－2m－6) ＝－4(m－4)(m－1－)(m－1＋)． 所以当且仅当m＝1－时，u(m)取到最大值． 故当且仅当m＝1－时，S取到最大值． 综上，所求直线l方程为3x＋2y＋2－2＝0.——————————————————— 直线与椭圆相交时的常见问题的处理方法 涉及问题处理方法弦长根与系数的关系、弦长公式中点弦或弦的中点点差法 5．(2013·洛阳模拟)已知椭圆＋＝1(a>b>0)的离心率为，短轴的一个端点为M(0,1)，直线l：y＝kx－与椭圆相交于不同的两点A，B. (1)若|AB|＝，求k的值； (2)求证：不论k取何值，以AB为直径的圆恒过点M. 解：(1)由题意知＝，b＝1. 由a2＝b2＋c2可得c＝b＝1，a＝， 椭圆的方程为＋y2＝1. 由得(2k2＋1)x2－kx－＝0. Δ＝k2－4(2k2＋1)×＝16k2＋>0恒成立． 设A(x1，y1)，B(x2，x2)， 则x1＋x2＝，x1x2＝－， |AB|＝·|x1－x2|＝·＝＝， 化简得23k4－13k2－10＝0，即(k2－1)(23k2＋10)＝0， 解得k＝±1. (2)证明：＝(x1，y1－1)，＝(x2，y2－1)， ·＝x1x2＋(y1－1)(y2－1) ＝(1＋k2)x1x2－k(x1＋x2)＋ ＝－－＋ ＝0. 不论k取何值，以AB为直径的圆恒过点M. 1个规律——椭圆焦点位置与x2、y2系数之间的关系 给出椭圆方程＋＝1时，椭圆的焦点在x轴上m>n>0；椭圆的焦点在y轴上0<m<n. 1种思想——数形结合思想在椭圆几何性质中的运用 求解与椭圆几何性质有关的问题时要结合图形进行分析，即使不画出图形，思考时也要联想到图形．当涉及到顶点、焦点、长轴、短轴等椭圆的基本量时，要理清它们之间的关系，挖掘出它们之间的内在联系． 2种方法——求椭圆标准方程的方法 (1)定义法：根据椭圆定义，确定a2，b2的值，再结合焦点位置，直接写出椭圆方程． (2)待定系数法：根据椭圆焦点是在x轴还是y轴上，设出相应形式的标准方程，然后根据条件确定关于a、b、c的方程组，解出a2、b2，从而写出椭圆的标准方程． 3种技巧——与椭圆性质、方程相关的三种技巧 (1)椭圆上任意一点M到焦点F的所有距离中，长轴端点到焦点的距离分别为最大距离和最小距离，且最大距离为a＋c，最小距离为a－c. (2)求椭圆离心率e时，只要求出a，b，c的一个齐次方程，再结合b2＝a2－c2就可求得e(0<e0”是“方程mx2＋ny2＝1的曲线是椭圆”的( ) A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 解析：选B　因为当m<0，n0，n>0，mn>0. 2．已知椭圆：＋＝1的焦距为4，则m等于( ) A．4 B．8 C．4或8 D．以上均不对 解析：选C　由得2<mb>0)的左、右焦点，P为直线x＝上一点，F2PF1是底角为30°的等腰三角形，则E的离心率为( ) A. B. C. D. 解析：选C　根据题意直线PF2的倾斜角是，所以a－c＝|PF2|＝|F1F2|＝×2c，解得e＝. 二、填空题(本大题共3小题，每小题5分，共15分) 7．若椭圆＋＝1(a>b>0)与曲线x2＋y2＝a2－b2恒有公共点，则椭圆的离心率e的取值范围是__________． 解析：由题意知，以半焦距c为半径的圆与椭圆有公共点，故b≤c，所以b2≤c2，即a2≤2c2， 所以≤.又<1，所以≤eb>0)的左、右顶点分别是A，B，左、右焦点分别是F1，F2.若|AF1|，|F1F2|，|F1B|成等比数列，则此椭圆的离心率为________． 解析：依题意得|F1F2|2＝|AF1|·|BF1|，即4c2＝(a－c)·(a＋c)＝a2－c2，整理得5c2＝a2，得e＝＝. 答案： 9．已知椭圆C：＋＝1(a>b>0)的离心率为.过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A，B两点．若＝3，则k＝________. 解析：根据已知＝，可得a2＝c2，则b2＝c2，故椭圆方程为＋＝1，即3x2＋12y2－4c2＝0.设直线的方程为x＝my＋c，代入椭圆方程得(3m2＋12)y2＋6mcy－c2＝0.设A(x1，y1)，B(x2，y2)，则根据＝3，得(c－x1，－y1)＝3(x2－c，y2)，由此得－y1＝3y2，根据韦达定理y1＋y2＝－，y1y2＝－，把－y1＝3y2代入得，y2＝，－3y＝－，故9m2＝m2＋4，故m2＝，从而k2＝2，k＝±. 又k>0，故k＝. 答案： 三、解答题(本大题共3小题，每小题12分，共36分) 10．已知P点在以坐标轴为对称轴的椭圆上，点P到两焦点的距离分别为和，过P点作焦点所在轴的垂线，它恰好过椭圆的一个焦点，求椭圆方程． 解：设两焦点为F1，F2，且|PF1|＝，|PF2|＝. 由椭圆定义知2a＝|PF1|＋|PF2|＝2，即a＝. 由|PF1|>|PF2|知，|PF2|垂直焦点所在的对称轴， 所以在RtPF2F1中，sinPF1F2＝＝. 可求出PF1F2＝，2c＝|PF1|·cos＝， 从而b2＝a2－c2＝. 所以所求椭圆方程为＋＝1或＋＝1. 11．已知椭圆G：＋＝1(a>b>0)的离心率为，右焦点为(2，0)．斜率为1的直线l与椭圆G交于A，B两点，以AB为底边作等腰三角形，顶点为P(－3,2)． (1)求椭圆G的方程； (2)求PAB的面积． 解：(1)由已知得c＝2，＝，解得a＝2， 又b2＝a2－c2＝4. 所以椭圆G的方程为＋＝1. (2)设直线l的方程为y＝x＋m. 由得4x2＋6mx＋3m2－12＝0. 设A，B的坐标分别为(x1，y1)，(x2，y2)(x1b>0)，右焦点为F2(c,0)． 因AB1B2是直角三角形，又|AB1|＝|AB2|， 故B1AB2为直角，因此|OA|＝|OB2|，得b＝. 结合c2＝a2－b2得4b2＝a2－b2，故a2＝5b2， c2＝4b2，所以离心率e＝＝. 在Rt△AB1B2中，OAB1B2，故 SAB1B2＝·|B1B2|·|OA|＝|OB2|·|OA|＝·b＝b2. 由题设条件SAB1B2＝4，得b2＝4，从而a2＝5b2＝20. 因此所求椭圆的标准方程为＋＝1. (2)由(1)知B1(－2,0)，B2(2,0)．由题意知直线l的倾斜角不为0，故可设直线l的方程为x＝my－2.代入椭圆方程得(m2＋5)y2－4my－16＝0. 设P(x1，y1)，Q(x2，y2)，则y1，y2是上面方程的两根， 因此y1＋y2＝，y1·y2＝－， 又＝(x1－2，y1)，＝(x2－2，y2)，所以 ·＝(x1－2)(x2－2)＋y1y2 ＝(my1－4)(my2－4)＋y1y2 ＝(m2＋1)y1y2－4m(y1＋y2)＋16 ＝－－＋16 ＝－， 由PB2⊥QB2，得·＝0，即16m2－64＝0， 解得m＝±2. 所以满足条件的直线有两条，其方程分别为x＋2y＋2＝0和x－2y＋2＝0. 1．设e1，e2分别为具有公共焦点F1与F2的椭圆和双曲线的离心率，P为两曲线的一个公共点，且满足1·2＝0，则的值为________． 解析：设椭圆的长半轴长为a1，双曲线的实半轴长为a2，|F1F2|＝2c，由题意得|PF1|＋|PF2|＝2a1，||PF1|－|PF2||＝2a2，|PF1|2＋|PF2|2＝2a＋2a. 又1·2＝0，PF1⊥PF2. ∴|PF1|2＋|PF2|2＝|F1F2|2，即2a＋2a＝4c2. 2＋2＝2，即＋＝2，即＝2. 答案：2 2．已知F1，F2为椭圆＋＝1(0<b<10)的左、右焦点，P是椭圆上一点． (1)求|PF1|·|PF2|的最大值； (2)若F1PF2＝60°且F1PF2的面积为，求b的值． 解析：(1)由题意得|PF1|＋|PF2|＝20，则|PF1|·|PF2|≤2＝100，当且仅当|PF1|＝|PF2|时，等号成立，故(|PF1|·|PF2|)max＝100. (2)因为SF1PF2＝|PF1|·|PF2|sin 60°＝， 所以|PF1|·|PF2|＝. 又 所以3|PF1|·|PF2|＝400－4c2. 由得c＝6，则b＝＝8. 3．已知平面内曲线C上的动点到定点(，0)和定直线x＝2的比等于. (1)求该曲线C的方程； (2)设动点P满足＝＋2，其中M，N是曲线C上的点．直线OM与ON斜率之积为－.问：是否存在两个定点F1，F2，使得|PF1|＋|PF2|为定值？若存在，求F1，F2的坐标；若不存在，说明理由． 解：(1)设曲线C上动点的坐标为(x，y)，根据已知得＝，化简整理得＋＝1，即为曲线C的方程． (2)设P(x，y)，M(x1，y1)，N(x2，y2)，则由＝＋2得(x，y)＝(x1，y1)＋2(x2，y2)， 即x＝x1＋2x2，y＝y1＋2y2， 因为点M，N在椭圆＋＝1上， 所以x＋2y＝4，x＋2y＝4， 故x2＋2y2＝(x＋4x＋4x1x2)＋2(y＋4y＋4y1y2) ＝(x＋2y)＋4(x＋2y)＋4(x1x2＋2y1y2) ＝20＋4(x1x2＋2y1y2)． 设kOM，kON分别为直线OM，ON的斜率，由题意知， kOM·kON＝＝－，因此x1x2＋2y1y2＝0， 所以x2＋2y2＝20， 所以P点是椭圆＋＝1上的点，设该椭圆的左、右焦点为F1、F2，则由椭圆的定义，|PF1|＋|PF2|为定值，又因为c＝ ＝，因此两焦点的坐标分别为F1(－，0)、F2(，0)．。

（全国通用版）2019版高考数学一轮复习第八章平面解析几何课时分层作业四十九8.5.1 椭圆的概念及其性质文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（全国通用版）2019版高考数学一轮复习第八章平面解析几何课时分层作业四十九8.5.1 椭圆的概念及其性质文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（全国通用版）2019版高考数学一轮复习第八章平面解析几何课时分层作业四十九8.5.1 椭圆的概念及其性质文的全部内容。

课时分层作业四十九椭圆的概念及其性质一、选择题(每小题5分，共35分）1。

椭圆x2+4y2=1的离心率为( ）A.B。

C.D。

【解析】选A。

因为椭圆方程化为x2+=1,所以c==,离心率e==.2。

设P是椭圆+=1上的点.若F1,F2是椭圆的两个焦点，则|PF1|+｜PF2|等于( ) A。

4 B。

5 C.8 D。

10【解析】选D.由椭圆的第一定义知｜PF1|+｜PF2|=2a=10.3。

已知动点P(x，y)与两点A1(—2，0)，A2(2,0）的连线斜率之积为·=-,则点P(x,y)的轨迹方程为（）A.+=1（y≠0）B。

+=1(y≠0）C。

+y2=1（y≠0） D.+=1(y≠0）【解析】选B.因为·=·=-,整理得+=1.又因为点P不能在x 轴上，所以y≠0。

【变式备选】若过椭圆的一个焦点作长轴的垂线,交椭圆于两点P,Q，线段PQ的长度为2,椭圆的一个焦点是(2,0)，则椭圆的标准方程是_________.【解析】由题意可知，=2，c=2，又因为a2=b2+c2,解得a2=80，b2=20，所求椭圆的标准方程为+=1.答案:+=14.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是（）A.B。