图形的对称

关于对称图形的关键概念对称图形是数学中一个重要的概念，它在几何学、代数学和计算机图形学等领域都有广泛的应用。

对称图形具有某种轴对称或中心对称的性质，使得它在进行变换时可以保持不变。

本文将通过介绍对称图形的基本概念、分类和性质，深入探讨对称图形在不同领域中的应用。

首先，对称图形的基本概念是指围绕轴线或中心进行的变换，并且变换前后的图形完全一致。

轴对称是指存在一个轴线，使得通过轴线将图形分割成两个完全相同的部分。

中心对称是指存在一个中心点，使得以中心点为对称中心将图形旋转180度后仍然保持不变。

在对称图形中，轴线或中心点是关键因素，它们决定了图形的对称性质。

对称图形的分类主要有轴对称图形和中心对称图形两类。

轴对称图形是指存在一个轴线，使得图形关于轴线对称。

常见的轴对称图形有长方形、正方形、菱形等。

而中心对称图形是指存在一个中心点，使得图形绕中心点旋转180度后保持不变。

常见的中心对称图形有圆形、星形等。

轴对称图形和中心对称图形是对称图形的两种基本类型，它们在对称性质上有所不同。

对称图形具有一些重要的性质，这些性质对于理解对称图形的本质及应用非常重要。

首先，对称图形是稳定的，即在进行对称变换后，图形的形状、大小和位置都不变。

其次，对称图形的对称轴和对称中心是唯一的，即通过对称轴或对称中心进行的变换可以保持图形不变，而其他轴线或点不能实现这一性质。

此外，对称图形的对称轴和对称中心具有一些特殊的性质，如对称轴上的每个点与对称轴上的另一个点的距离相等，在中心对称图形中，中心点到图形中任意点的距离相等。

对称图形具有广泛的应用，其中在几何学和计算机图形学中的应用较为突出。

在几何学中，对称图形是研究几何变换的基础，通过对称性的研究可以得到一些重要的结论，如轴对称图形的对称轴和对称中心的性质。

在计算机图形学中，对称图形常用于生成具有对称性质的图案和模型，如建模中的对称约束、图案的生成和纹理的设计等。

此外，对称图形还在代数学中有着重要的应用，如群论中对称群的研究。

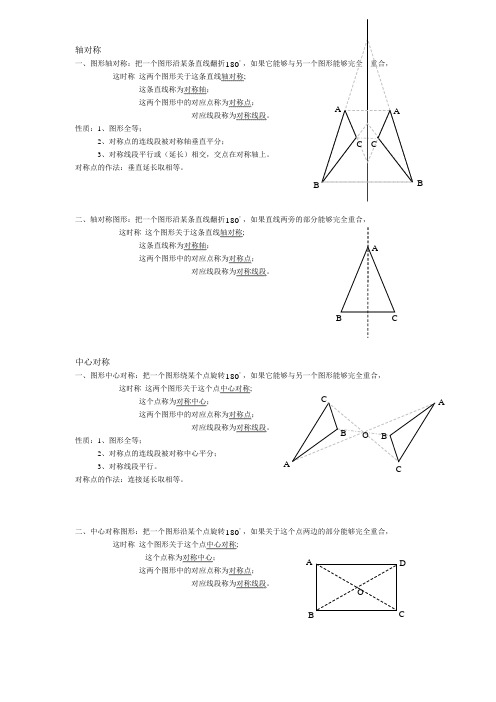
轴对称
一、图形轴对称：把一个图形沿某条直线翻折︒180，如果它能够与另一个图形能够完全 重合，
这时称 这两个图形关于这条直线轴对称;
这条直线称为对称轴；
这两个图形中的对应点称为对称点； 对应线段称为对称线段。

性质：1、图形全等；
2、对称点的连线段被对称轴垂直平分；
3、对称线段平行或（延长）相交，交点在对称轴上。

对称点的作法：垂直延长取相等。

二、轴对称图形：把一个图形沿某条直线翻折︒180，如果直线两旁的部分能够完全重合，
这时称 这个图形关于这条直线轴对称; 这条直线称为对称轴；
这两个图形中的对应点称为对称点； 对应线段称为对称线段。

中心对称
一、图形中心对称：把一个图形绕某个点旋转︒180，如果它能够与另一个图形能够完全重合，
这时称 这两个图形关于这个点中心对称; 这个点称为对称中心；
这两个图形中的对应点称为对称点； 对应线段称为对称线段。

性质：1、图形全等；
2、对称点的连线段被对称中心平分；
3、对称线段平行。

对称点的作法：连接延长取相等。

二、中心对称图形：把一个图形沿某个点旋转︒180，如果关于这个点两边的部分能够完全重合，
这时称 这个图形关于这个点中心对称; 这个点称为对称中心；
这两个图形中的对应点称为对称点； 对应线段称为对称线段。

A
B C
A
B
C
D
O
A
A
B
B
C C
A
C。

八年级对称图形知识点对称图形是一种美丽而神秘的艺术形式，在日常生活和自然界中随处可见。

在数学学科中，对称图形也是一个非常重要的概念，它涵盖了对称轴、对称中心、轴对称图形和中心对称图形等多个知识点。

在本文中，我们将介绍八年级对称图形知识点的相关内容。

一、对称轴对称轴是指将一个图形分为两个完全相同的部分的直线。

对称轴是轴对称图形的重要概念，它有以下几个特点：（1）对称轴过图形的中心点。

（2）对称轴两侧的部分互为镜像，即对称轴将图形分成两个相似的部分。

（3）对称轴可以是直线、射线或线段。

在计算对称轴时，要注意图形的位置和形状。

正方形、长方形和圆等常见对称图形的对称轴比较容易计算，但对称轴不是直线的不规则图形就需要用推理和衍生的方法计算。

二、对称中心对称中心是指将一个图形分为两个完全相同的部分的点。

对称中心是中心对称图形的重要概念，它有以下几个特点：（1）对称中心是图形的中心点。

（2）对称中心两侧的部分互为镜像，即对称中心将图形分成两个相似的部分。

（3）对称中心可以在图形内部或外部。

在计算对称中心时，要注意图形的形状和对称性。

对称中心可以通过描画图形的所有对角线，通过交点找到。

也可以通过测量图形两侧的长度和角度来找到。

三、轴对称图形轴对称图形是指将一个图形沿着某个对称轴折叠后，两侧完全重合的图形。

轴对称图形有以下几个特点：（1）轴对称图形的所有点可以通过对称轴进行对称得到。

（2）轴对称图形的两侧完全相同，形状和大小完全相同。

（3）轴对称图形可以是二维平面图形，也可以是三维立体图形。

轴对称图形在日常生活和数学学科中都有广泛的应用。

例如矩形、圆形、星形、心形等常见图形都是轴对称图形，它们在建筑、装饰、艺术和游戏等领域都有重要的应用。

四、中心对称图形中心对称图形是指将一个图形沿着某个对称中心旋转180度后，完全重合的图形。

中心对称图形有以下几个特点：（1）中心对称图形的所有点可以通过对称中心旋转180度得到。

图形的变化与对称一、图形的变换1.平移：在平面内，将一个图形整体按照某个直线方向移动一定的距离，这种移动叫做图形的平移。

2.旋转：在平面内，将一个图形绕一点按某个方向转动一个角度，这种移动叫做图形的旋转。

3.轴对称：在平面内，如果一个图形沿一条直线对折，对折后的两部分都能完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴。

二、图形的对称性1.对称轴：一个图形沿一条直线对折，对折后的两部分都能完全重合，这条直线就叫做这个图形的对称轴。

2.对称点：一个图形沿一条直线对折，对折后的两部分都能完全重合，这个图形的每个点都有一个对应的对称点。

3.中心对称：在平面内，如果把一个图形绕某一点旋转180°，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心。

三、图形的对称性质1.对称图形的性质：对称图形的大小、形状和位置都不变，只是位置发生了变化。

2.轴对称图形的性质：轴对称图形沿对称轴对折，对折后的两部分完全重合。

3.中心对称图形的性质：中心对称图形绕对称中心旋转180°，旋转后的图形和原图形完全重合。

四、图形的变换与对称的应用1.利用图形的变换与对称解决实际问题，如设计图案、解决几何题等。

2.了解图形的变换与对称在生活中的应用，如建筑设计、艺术创作等。

1.判断题：（1）平移是将图形沿着一个方向移动一定的距离。

（）（2）旋转是将图形绕一个点转动一个角度。

（）（3）如果一个图形沿一条直线对折，对折后的两部分完全重合，这个图形就是轴对称图形。

（）（4）对称轴是将图形分成两个完全相同部分的一条直线。

（）2.选择题：（1）以下哪个选项不是图形的变换？（）A.平移B.旋转C.翻转D.缩放（2）一个图形沿一条直线对折，对折后的两部分完全重合，这个图形沿该直线叫做什么？( )A.对称轴B.对称点C.对称线D.对称面3.解答题：（1）请描述轴对称图形的特点。

（2）请描述中心对称图形的特点。

性质2023-10-30CATALOGUE 目录•轴对称图形概述•轴对称图形的性质•常见轴对称图形举例•非轴对称图形举例及特性•轴对称图形的应用01轴对称图形概述定义如果一个图形关于某条直线（称轴）对称，那么这个图形叫做轴对称图形。

性质轴对称图形的对称轴也是图形的中垂线，即线段的中点与轴对称图形上相对应点的连线被对称轴垂直平分。

轴对称图形的定义轴对称图形具有对称性，即图形的左右两侧或上下两侧关于某条直线对称。

对称性唯一性美观性每一个轴对称图形都只有一个对称轴，对称轴将图形分成两个完全相同的部分。

轴对称图形具有美观性，常被应用于建筑设计、艺术和日常生活中。

03轴对称图形的特点0201轴对称图形在数学、艺术、建筑等领域有着悠久的历史。

早在古希腊和罗马时期，人们就利用轴对称来设计建筑、雕塑和图案。

历史随着数学、计算机科学和工程技术的进步，轴对称图形在各个领域的应用越来越广泛，如建筑设计、工业设计、计算机图形学等。

同时，对于轴对称图形的理论研究也在不断发展与完善。

发展轴对称图形的历史与发展02轴对称图形的性质总结词轴对称图形在空间或平面上关于某条直线（称为对称轴）具有对称性。

详细描述这意味着图形的一部分相对于对称轴的镜像翻转后，与另一部分完全重合。

例如，一个圆相对于其直径是对称的，一个正方形相对于其对角线是对称的。

这种对称性在自然界中也很常见，如人的身体、树叶等。

总结词轴对称图形的对称轴总是一条直线，且具有平行性。

详细描述这意味着如果一个图形的一部分相对于对称轴进行镜像翻转后，与另一部分完全重合，那么这两部分必然是平行的。

例如，一个矩形相对于其对边中点的连线是对称的，这个连线就是其对称轴。

轴对称图形的性质三总结词轴对称图形的对称轴具有镜像反射性。

详细描述这意味着图形的一部分相对于对称轴的镜像反射后，与另一部分完全重合。

这种性质可以用来解释许多自然现象和社会现象，如物体在水中的倒影、物体在镜子中的影像等。

怎样判断中心对称图形
中心对称图形判定简单方法：1、有对称中心。

2、如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称。

中心对称图形的定义：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。

中心对称和中心对称图形是两个不同而又紧密联系的概念。

区别是：中心对称是指两个全等图形之间的相互位置关系，这两个图形关于一点对称，这个点是对称中心，两个图形关于点的对称也叫做中心对称。

成中心对称的两个图形中，其中一个图形上所有点关于对称中心的对称点都在另一个图形上，反之，另一个图形上所有点的对称点，又都在这个图形上；而中心对称图形是指一个图形本身成中心对称。

中心对称图形上所有点关于对称中心的对称点都在这个图形本身上。

如果将中心对称的两个图形看成一个整体（一个图形），那么这个图形就是中心对称图形；一个中心对称图形，如果把对称的部分看成是两个图形，那么它们又是关于中心对称。

关于中心对称的两个图形是全等形。

关于中心对称的两个图形，对称点所连线段都经过对称中心，并且被对称中心所平分。

关于中心对称的两个图形，对应线段平行（或者在同一直线上）且相等。