第一章《数与式》考点
- 格式:doc
- 大小:131.00 KB
- 文档页数:6


2024年中考数学总复习第一章《数与式》第一节:实数★解读课标★--------------熟悉课标要求,精准把握考点1.理解有理数的意义,能用数轴上的点表示有理数,能比较有理数的大小;了解无理数和实数的概念,知道实数与数轴上的点一一对应,能求实数的相反数与绝对值;2.借助数轴理解相反数和绝对值的意义,掌握求有理数的相反数与绝对值的方法,知道|a|的含义;3.会用科学记数法表示数;4.了解平方根、算术平方根、立方根的概念.会用根号表示数的平方根、算术平方根、立方根,会用平方运算求百以内整数的平方根;5.掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步以内为主);能运用有理数的运算解决简单的问题.★中考预测★--------------统计考题频次,把握中考方向1.实数与运算在历年中考中以考查基础为主,也是考查重点,年年考查,是广大考生的得分点,分值为14~28分。
2.预计2024年各地中考还将继续重视对正负数的意义、相反数、绝对值、倒数、数轴等实数的相关概念及实数的分类的考查,也会对有理数的运算、科学记数法、数的开方、零次幂、负整数指数幂、二次根式及运算等进行考查,且考查形式多样,为避免丢分,学生应扎实掌握。
★聚焦考点★--------------直击中考考点,落实核心素养有理数及其相关概念1.整数和分数统称为有理数。
(有限小数与无限循环小数都是有理数。
)2.正整数、0、负整数统称为整数。
正分数、负分数统称分数。
3.正数和零统称为非负数,负数和零统称为非正数,正整数和零统称为非负整数,负整数和零统称为非正整数。
4.正数和负数表示相反意义的量。
【注意】0既不是正数,也不是负数。
数轴 1.数轴的三要素:原点、正方向、单位长度。
数轴是一条直线。
2.所有有理数都可以用数轴上的点来表示,但数轴上的点不一定都是有理数。
3.数轴上,右边的数总比左边的数大;表示正数的点在原点的右侧,表第1页共44页。


中考数学重点难点分值题型分布第一章数与式1.1实数考点1:实数的分类与实数的有关概念掌握题型:选择题、填空题; 分值:3分考试内容:1.实数的定义与分类2.实数的大小比较3.数轴4.相反数、倒数、绝对值5.无理数的估算考点2:实数的运算掌握题型:选择题、填空题;分值:3分、4分考试内容:1.平方根与立方根2.实数的混合运算考点3:科学计数法掌握与近似数了解题型:选择题;分值:3分考试内容:1.科学记数法2.近似数1.2代数式考点1:代数式理解——必考点题型:选择题;分值:4分考试内容:1.列代数式表示简单的数量关系2.能解释一些简单代数式的实际意义或几何意义考点2:求代数式的值题型:解答题;分值:6分考试内容:1.代数式的值的概念“了解2.根据问题所提供的资料,求代数式的值1.3整式考点1:整式及其运算灵活运用题型:填空题;分值:3分考试内容:1.整式的有关概念了解2.整数指数幂的意义和基本性质了解3.整式加减乘除法运算的法则4.会进行简单的整式加减乘除法运算考点2:整式乘法公式灵活运用——必考点题型:填空题;分值:3分、4分考试内容:1.完全平方公式、平方差公式的几何背景了解2.平方差公式、完全平方公式3.用平方差公式、完全平方公式进行简单计算考点3:因式分解灵活运用题型:填空题;分值:3分、4分考试内容:1.因式分解的意义及其与整式乘法之间的关系了解2.用提取公因式法、、公式法进行因式分解,会在实数范围内分解因式1.4分式与二次根式考点1:分式的概念与基本性质灵活运用——必考点题型:选择题;分值:3分考试内容:1.分式的概念了解2.确定分式有意义的条件3.确定使分式的值为零的条件4.分式的基本性质5.约分和通分考点2:分式的运算掌握——必考点题型:解答题;分值:6分考试内容:1.分式的加、减、乘、除、乘方运算法则2.简单的分式加减乘除乘方运算,用恰当方法解决与分式有关的问题考点3:二次根式掌握——必考点题型:选择题;分值:3分1.二次根式的概念2.最简二次根式3.二次根式的运算第二章方程组与不等式组2.1整式方程考点1:一元一次方程掌握,灵活运用题型:选择题、解答题;分值:3分、6分、8分考试内容:1.方程是刻画现实世界数量关系的一个数学模型了解2.运用一元一次方程解决简单的实际问题3.方程的解的概念了解4.由方程的解求方程中字母系数的值5.一元一次方程的有关概念了解6.一元一次方程的解法考点2:一元二次方程掌握,灵活运用——必考点题型:选择题、填空题;分值:3分、4分1.一元二次方程的概念了解2.一元二次方程的解法3.用一元二次方程根的判别式判断根的情况4.运用一元二次方程解决简单的实际问题2.2分式方程考点1:分式方程及其解法——必考点题型:选择题、填空题;分值:3分、4分考试内容:1.分式方程的概念2.分式方程的增根3.分式方程的求解4.分式方程的检验考点2:分式方程的应用题型:解答题;分值:10分考试内容:1.利用分式方程解决生活实际问题2.注意分式方程要对方程和实际意义进行双检验2.3方程组考点1:二元一次方程组题型:解答题;分值:7分考试内容:1.二元一次方程组的有关概念了解2.代入消元法、加减消元法的意义3.选择适当的方法解二元一次方程组考点2:二元一次方程组的应用——必考点题型:解答题;分值:9分考试内容:运用二元一次方程组解决简单的实际问题2.4不等式组考点1:不等式和一元一次不等式组题型:选择题、填空题;分值:3分、4分考试内容:1.不等式的意义了解2.根据具体问题中的数量关系列出不等式3.不等式的基本性质4.利用不等式的性质比较两个实数的大小5.一元一次不等式的解集了解6.解不等式组考点2:一元一次不等式组的应用——必考点题型:解答题;分值:8分考试内容:根据具体问题中的数量关系,用一元一次不等式或不等式组解决简单问题第三章变量与函数3.1位置的确定与变量之间的关系考点1:平面直角坐标系题型:选择题、填空题;分值:3分考试内容:1.坐标平面内点的坐标特征的运用2.坐标轴、原点对称的点的坐标的特征考点2:函数及其图象题型:选择题、填空题;分值:3分、8分考试内容:1.求函数自变量的取值范围2.根据条件写出函数关系式3.用描点法画出函数图像考点3:函数的有关应用题型:选择题;分值:3分考试内容:解决与函数有关的应用型问题3.2一次函数考点1:一次函数的概念、图象和性质题型:解答题;分值:3分、10分考试内容:1.对一次函数概念的理解理解2.根据已知条件用待定系数法确定函数解析式3.会画一次函数图象并能根据图象解决相关的问题4.根据自变量的变化判断函数值的增减情况灵活运用5.由函数值的取值范围判断自变量的取值范围,求一次函数图象的交点坐标考点2:一次函数的应用题型:解答题;分值:9分考试内容:与一次函数有关的应用问题灵活运用3.3反比例函数考点1:求反比例函数解析式题型:填空题;分值:4分考试内容:1.对反比例函数的理解2.根据已知条件用待定系数法确定反比例函数解析式考点2:反比例函数的图象和性质题型:解答题;分值:8分考试内容:1.会画反比例函数的增减性;掌握比例系数K的几何意义考点3:反比例函数的应用题型:填空题、解答题;分值:3分、9分考试内容:1.反比例函数与一次函数图象与性质的综合应用2.确定与反比例函数有关的应用型问题3.4二次函数考点1:二次函数的图象和性质题型:选择题、解答题;分值: 3分、3分考试内容:1.用配方法把抛物线的解析式y=ax2+bx+ca≠0化为y=ax-h2+ka≠0的形式2.根据已知条件用待定系数法确定二次函数的解析式3.根据抛物线的位置确定a、b、c的符号,根据公式确定抛物线的顶点和对称轴4.根据自变量的变化判断二次函数值的增减情况5.根据函数图象求一元二次方程的根,由一元二次方程根的情况判断抛物线与x轴的交点;根据图象判断一元二次不等式的解集考点2:二次函数的综合应用题型:解答题;分值:10分、12分考试内容:1.利用二次函数解决简单的实际问题2.与二次函数有关的综合应用第四章图形的认识4.1角、相交线与平行线考点1:角题型:选择题;分值:3分考试内容:1.角的有关概念了解2.角的比较、角的和差计算3.余角、补角考点2:相交线题型:选择题;分值:3分考试内容:1.对顶角2.垂线、点到直线的距离3.作已知直线的垂线4.命题、定理、证明考点3:平行线题型:选择题;分值:3分考试内容:1.平行线的性质2.平行线间的距离3.平行线的判定4.2三角形及其全等考点1:三角形的相关概念题型:选择题;分值:3分考试内容:1.角平分线、中线、高线、中位线以及性质2.画任意三角形的角平分线、中线和高3.三角形的稳定性、三边关系定理、三角形内角和定理考点2:三角形全等题型:填空题、解答题;分值:3分考试内容:1.全等三角形对应边相等、对应角相等2.三角形全等的判定定理:SAS, ASA, AAS, SSS, HL 4.3等腰三角形与直角三角形考点1:等腰三角形题型:选择题;分值:3分考试内容:1.等腰三角形的有关概念、性质和判定2.等边三角形的有关概念、性质和判定考点2:直角三角形题型:选择题;分值:3分考试内容:1.直角三角形的概念、性质和判定2.勾股定理及其逆定理:4.4多边形与平行四边形考点1:多边形题型:选择题;分值:3分考试内容:多边形和正多边形的概念、内角和与外角和公式了解考点2:平行四边形题型:解答题;分值:9分考试内容:1、平行四边形的概念和性质2、平行四边形的判定4.5特殊的平行四边形考点1:矩形题型:选择题、填空题、解答题;分值:3分、8分考试内容:1.矩形的概念、性质2.矩形的判定考点2:菱形题型:选择、解答;分值:3分、10分考试内容:1、菱形的概念、性质2、菱形的判定考点3:正方形题型:选择题、解答题;分值:3分考试内容:1.正方形具有矩形和菱形的性质2.既是矩形又是菱形的四边形是正方形4.6梯形依据考情选用题型:填空题;分值:3分考试内容:1.梯形的概念和性质2.等腰梯形的概念、性质和判定3.直角梯形的概念第五章圆5.1圆的性质及与圆有关的位置关系考点1:圆的有关概念与性质题型:选择题、解答题;分值:3分、4分、9分考试内容:1.垂径定理及其推论的应用2.弧、圆心角、圆周角之间的关系3.圆周角定理及其推论考点2:与圆有关的位置关系题型:选择题、解答题考试内容:1.点和圆的位置关系2.直线和圆的位置关系3.切线的性质和判定5.2与圆有关的计算题型:选择题、填空题、解答题;分值:3分、10分考试内容:1.求圆的周长、弧长及简单组合图形的周长2.求圆的面积、扇形的面积及简单组合图形的面积3.圆柱的侧面积和全面积的计算4.圆锥的侧面积和全面积的计算第六章空间与图形6.1圆形的轴对称、平移与旋转考点1:轴对称的概念及性质题型:选择题;分值:3分考试内容:1.轴对称的概念及性质2.基本图形的对称性及轴对称的应用考点2:图形的平移题型:选择题;分值:3分考试内容:1.平移的概念和性质2.简单图形的平移及平移的应用考点3:图形的旋转题型:选择题;分值:3分考试内容:1.旋转的概念及性质2.基本图形的旋转及旋转的应用6.2图形的相似考点1:相似的有关概念题型:近5年未考考试内容:成比例线段、比例的基本性质、黄金分割考点2:相似三角形的性质与判定题型:填空题;分值:3分考试内容:1.相似的概念及相似的判定2.相似的性质、多边形相似比、周长比与面积比考点3:位似的概念与性质题型:选择题;分值:3分考试内容:1.位似的概念和性质2.利用位似放大或缩小图形,会在坐标系中作位似图形并求出对应的坐标6.3解直角三角形题型:选择题、填空题、解答题;分值:3、6分考点1:锐角三角函数考试内容:1.锐角三角函数的定义及其性质2.特殊角的三角函数值考点2:解直角三角形考试内容:1.解直角三角形的概念2.直角三角形的边角关系3.仰角、俯角、坡度坡比4.用三角函数解决与直角三角形有关的实际问题6.4视图与投影考点1:几何体及其展开图题型:选择题;分值:3分考试内容:基本几何体的展开图考点2:几何体的三视图题型:选择题;分值:3分考试内容:画基本几何体或简单组合体的三视图,根据三视图描述实物考点3:投影题型:近五年未考考试内容:1.中心投影和平行投影2.影子、视点、视角和盲区的概念第七章统计与概率7.1统计考点1:数据的收集题型:选择题;分值:3分考试内容:1.普查和抽样调查2.总体、个体、样本和样本容量3.用样本估计总体的思想考点2:数据的处理题型:选择题;分值:3分考试内容:1.求一组数据的平均数包括加权平均数、众数、中位数、极差与方差2.根据具体问题,选择合适的统计量表示数据的集中程度或离散程度3.根据统计结果做出合理的判断和预测考点3:统计图表题型:解答题;分值:4分、8分考试内容:1.用扇形统计图表示数据2.频数、频率的概念,频数分布的意义和作用3.列频数分布表,画频数分布直方图和频数分布折线图4.利用统计图表解决简单的实际问题7.2概率考点1:事件的分类题型:选择题;分值:3分考试内容:不可能事件、必然事件和随机事件考点2:概率的计算题型:解答题;分值:10分考试内容:1.概率的意义2.运用列举法包括列表、画树状图计算简单事件发生的概率考点3:用频率估计概率题型:填空题;分值:3分考试内容:大量重复试验时,可以用频率估计概率解决一些实际问题。
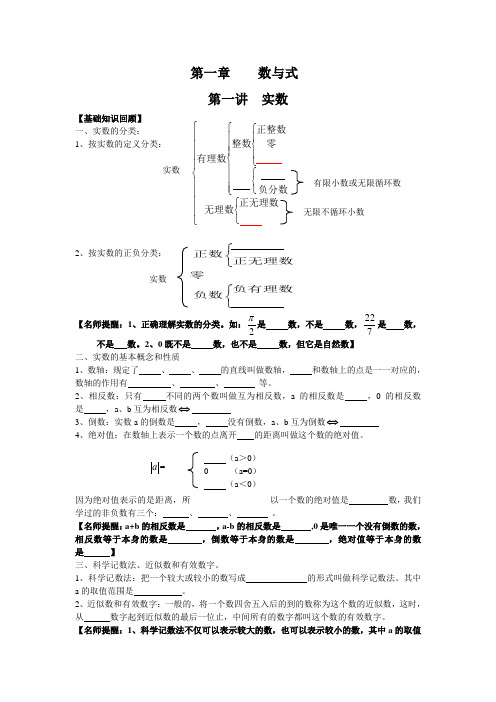
第一章 数与式第一讲 实数【基础知识回顾】 一、实数的分类: 1、按实数的定义分类: 实数 有限小数或无限循环数2、按实数的正负分类:实数【名师提醒:1、正确理解实数的分类。
如:2π是 数,不是 数,722是 数,不是 数。
2、0既不是 数,也不是 数,但它是自然数】二、实数的基本概念和性质1、数轴:规定了 、 、 的直线叫做数轴, 和数轴上的点是一一对应的,数轴的作用有 、 、 等。
2、相反数:只有 不同的两个数叫做互为相反数,a 的相反数是 ,0的相反数是 ,a 、b 互为相反数⇔3、倒数:实数a 的倒数是 , 没有倒数,a 、b 互为倒数⇔4、绝对值:在数轴上表示一个数的点离开 的距离叫做这个数的绝对值。
a =因为绝对值表示的是距离,所以一个数的绝对值是 数,我们学过的非负数有三个: 、 、 。
【名师提醒:a+b 的相反数是 ,a-b 的相反数是 ,0是唯一一个没有倒数的数,相反数等于本身的数是 ,倒数等于本身的数是 ,绝对值等于本身的数是 】三、科学记数法、近似数和有效数字。
1、科学记数法:把一个较大或较小的数写成 的形式叫做科学记数法。
其中a 的取值范围是 。
2、近似数和有效数字:一般的,将一个数四舍五入后的到的数称为这个数的近似数,这时,从 数字起到近似数的最后一位止,中间所有的数字都叫这个数的有效数字。
【名师提醒:1、科学记数法不仅可以表示较大的数,也可以表示较小的数,其中a 的取值⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎨ ⎧ ⎩ ⎨ ⎧ ⎪ ⎩ ⎪ ⎨ ⎧ 正无理数 无理数 负分数 零 正整数 整数 有理数 无限不循环小数 ⎧⎨⎩⎧⎨⎩正数正无理数零 负有理数负数 (a >0) (a <0) 0 (a=0)范围一样,n 的取值不同,当表示较大数时,n 的值是原整数数位减一,表示较小的数时,n 是负整数,它的绝对值等于原数中左起第一个非零数字前零的个数(含整数数位上的零)。

第二章 方程(组)与不等式(组)第1讲 一元一次方程和二元一次方程组考点1 等式及方程的有关概念 1.等式及其性质(1)用“=”来表示相等关系的式子,叫做等式. (2) 等式的性质:①等式两边都加上(或减去)________________,所得的结果仍然是_______; ②等式两边都乘以(或除以)________________________,所得的结果仍然是________. 2.方程的有关概念(1) 含有_________的等式叫做方程. (2) 方程的解:______________________________________叫做方程的解.一元方程的解,也叫它的根).(3) 解方程:求方程解的过程叫做解方程.考点2 一次方程(组)的相关概念 1. 一元一次方程(1)概念:只含有______未知数,并且未知数的次数都是____,系数不等于零的________整式方程叫做一元一次方程.(2)标准形式(一般形式)___________________.2. 二元一次方程(1)概念:含有______未知数,并且含未知数的项的次数都是____,这样的方程叫做二元一次方程.(2)一般形式:________________________.(3) 使二元一次方程左右两边的值________的两个未知数的值,叫做二元一次方程的解.(4)解的特点:一般地,二元一次方程有无数个解. 3. 二元一次方程组(1) 概念:具有相同未知数的_______二元一次方程合在一起,就组成了一个二元一次方程组. (2)一般形式:(3) 二元一次方程组的解一般地,二元一次方程组的两个方程的_________,叫做二元一次方程组的解. 考点3 一次方程(组)的解法 1. 解一元一次方程的一般步骤(1) _______________ (2) _______________ (3) _______________ (4) _______________ (5) _______________ 2.二元一次方程组的解法解二元一次方程组的基本思想是_______,即化二元一次方程组为一元一次方程,主要等式 等式 同一个数(除数不能是零) 同一个数或整式 使方程左右两边的值相等的未知数的值 未知数 1 一个 ax +b =0(a ≠0) 整式 1 两个 相等 ax +by =c (a ≠0,b ≠0) a 1x +b 1y =c 1两个 (a 1,b 1,a 2,b 2均不为零) a 2x +b 2y =c 2公共解 去分母 合并同类项 去括号 化系数为1 移项 消元方法有______消元法和______消元法.(1)用代入消元法解二元一次方程组的一般步骤:①从方程组中选定一个系数比较简单的方程进行变形,用含有x(或y)的代数式表示出y(或x),即变成y=ax+b(或x=ay+b)的形式;②将y=ax+b(或x=ay+b)代入另一个方程,消去y(或x),得到关于x(或y)的一元一次方程;③解这个一元一次方程,求出x(或y)的值;④把x(或y)的值代入y=ax+b(或x=ay+b)中,求出y(或x)的值.(2) 用加减消元法解二元一次方程组的一般步骤:①在二元一次方程组中,若同一个未知数的系数相同(或互为相反数),则可以直接相减(或相加),消去一个未知数;②在二元一次方程组中,若不存在①中的情况,可选一个适当的数去乘方程的两边,使其中一个未知数的系数相同(或互为相反数),再把方程两边分别相减(或相加),消去一个未知数,得到一个一元一次方程;③解这个一元一次方程;④将求出的一元一次方程的解代入原方程组中系数比较简单的方程内,求出另一个未知数.考点4 一次方程(组)的应用1.步骤(1)设未知数;(2)列出方程(组);(3)解方程(组);(4)检验求得的未知数的值是否符合实际意义;(5)写出答案(包括单位名称).2.列出方程(组)常用的相等关系注:应用问题中的相等关系往往不止一个,解题时要选择合适的一个数量设未知数,根据另外的相等关系列出方程(组).第2讲一元二次方程考点1 一元二次方程的相关概念 1.定义:只含有________未知数,并且未知数的最高次数是_____的整式方程,叫做一元二次方程.2. 一元二次方程的一般形式:_____________________. 考点2 一元二次方程的解法1.直接开平方法:适用于能化成(x +a )²=b (b ≥0)的一元二次方程.2.配方法若x ²+px +q =0且p ²-4q ≥0,则(x +2p )²=-q +(2p )².x 1=-2p +22⎪⎭⎫ ⎝⎛+-p q ,x 2=-2p -22⎪⎭⎫ ⎝⎛+-p q 二次项系数不为1时,先在方程两边同时除以二次项系数,把二次项系数化为1. 3.公式法若ax ²+bx +c =0(a ≠0) 且b ²-4ac ≥0,则x =aac b b 242-±- .4.因式分解法 一般步骤:(1)将方程的右边各项移到左边,使右边为0; (2)将方程的左边分解为两个一次因式乘积的形式; (3)令每个因式为0,得到两个一元一次方程; (4)解这两个一元一次方程,他们的解就是原方程的解. 考点3 一元二次方程根的判别式及根与系数的关系 1. 一元二次方程根的判别式(1) b ²-4ac ≥0⇔ ax ²+bx +c =0(a ≠0)有两个________的实数根. (2) b ²-4ac =0⇔ ax ²+bx +c =0(a ≠0)有两个________的实数根. (3) b ²-4ac <0⇔ ax ²+bx +c =0(a ≠0)有两个________实数根. 2. 一元二次方程根与系数的关系若一元二次方程ax ²+bx +c =0(a ≠0) 有两个实数根x 1, x 2,则 x 1+x 2=a b -,x 1·x 2=ac. 3.*在一元二次方程ax ²+bx +c =0(a ≠0)中(1)有一个根为0,则c =______; (2)有一个根为1,则a +b +c =_____; (3)有一个根为-1,则a -b +c =______; (4)若两根互为相反数,则b =______,且b ²-4ac______; (5)若两根互为倒数,则c =______,且b ²-4ac______. 一个 ax ²+bx +c =0(a ≠0) 2 没有 不相等 相等 0 00 0 a ≥0 ≥0考点4 一元二次方程的应用列一元二次方程解应用题的步骤和列一元一次方程(组)解应用题的步骤基本一样. 基本题型有握手问题、增长率问题、传播问题、面积问题、销售问题等.第3讲 分式方程考点1 分式方程及其解法1.______里含有__________的方程叫做分式方程.2.解分式方程(1) 运用“转化”的思想,将分式方程转化为_______方程,转化的途径是“去分母”,即方程两边都乘__________________. (2) 解分式方程的步骤①将分式方程的各个分式的分母因式分解,找出最简__________; ②用最简公分母去乘分式方程的两边,将分式方程转化为_______方程; ③将求得的未知数的值代入最简公分母检验,看其是否为0;④若最简公分母为0,则原方程无解;若最简公分母不为0,则所求的解即为原方程的解. 考点2 分式方程的增根及特殊解1.增根:增根是使得原分式方程的分母等于______的整式方程的根.2.验根:方法①:把求得的未知数的值代入原方程中,看左右两边的值是否_________.方法②:把求得的未知数的值代入最简公分母,看最简公分母的值是否为_____.若值为_____,则此时未知数的值就是原方程的增根;若值不为_____,则此时未知数的值就是原方程的根.考点3 分式方程的应用列分式方程解应用题的一般步骤:(1)审题; (2)设未知数; (3)列方程; (4)解方程; (5)检验;(6)写答案.注:列分式方程解应用题与列整式方程解应用题的不同之处是所列方程是分式方程,最后一定要进行检验,既要检验其是否为所列分式方程的解,又要检验其是否符合实际意义.第4讲 一元一次不等式(组)考点1 不等式的有关概念及其性质1.不等式的有关概念(1)用_________表示大小关系的式子叫做不等式. (2) 一个含有_________的不等式的所有__________叫做不等式的解集. (3) 求不等式的解集______的过程叫做解不等式. 2.不等式的基本性质未知数 分母 整式 公分母 最简公分母 整式 相等 零 零 零 零 不等号 未知数 解的集合 解集(1) 不等式两边都加上(或减去)同一个数(或整式),不等号的方向不变,即若a <b , 则a ±c _____b ±c ; (2) 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变,即若a <b , 则且c >0,则ac _____bc (或c a _____cb ); (3) 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变,即若a <b , 则且c<0,则ac _____bc (或c a _____cb ). *不等式的其他性质:反射性:若a >b ,则b <a ; 传递性:若a >b ,且b >c ,则a >c.考点2 不等式(组)的解法1.一元一次不等式:只含有______未知数,且未知数的次数是1的不等式叫做一元一次不等式.2. 解一元一次不等式的基本步骤:_________、_________、_______、___________、___________.3. 一元一次不等式组:关于同一个未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.4. 一元一次不等式组的解集:一元一次不等式组中各个不等式解集的公共部分,叫做这个一元一次不等式组的解集.5. 一元一次不等式组的解集的确定方法 若a <b , 则有 考点3 确定不等式(组)中字母的取值范围若不等式(组)中含字母(第二个未知数),可以先将字母当作已知数处理,求出不等式(组)的解集,再结合已知条件求得字母的取值范围. 考点41.列不等式或不等式组解决实际问题,要注意抓住问题中的一些关键词语,如“至少”“最多”< < > < > 去分母 一个 系数化为1 x <b 合并同类项 (1)x <a 移项 去括号 (3) x <a a <x <b x <a x >b 空集 (2) (4) 的解集是__________,即“同小取小”;x >b x >a 的解集是__________,即“同大取大”; x >a 的解集是__________,即“大小小大中间找”;x <b (4)x >b的解集是__________,即“大大小小无处找”.“超过”“不低于”“不大于”“不高于”“大于”“多”等,这些都体现了不等关系,列不等式时,要根据关键词准确地选用不等号.另外,对一些实际问题的分析还要注意结合实际.2. 列不等式(组)解应用题的一般步骤:(1)审题;(2)设未知数;(3)找出能够包含未知数的不等量关系;(4)列出不等式(组);(5) 求出不等式(组)的解;(6)在不等式(组)的解中找出符合题意的值;(7)写出答案(包括单位名称).。