5.7 杆模型

杆的模型应用及受力情况分析中学物理研究问题的思想方法，虽然在课本中没有明确指出，但它已经渗透到各部分内容的叙述中，只要留心就会发现这样的事实，物理学研究问题时，往往先从大量的事实中，抽象出它们的化身———理想化模型(如描述物体的有：质点、点电荷等；描述运动的有：匀变速直线运动、匀速圆周运动、简諧振动等；描述过程的有：弹性碰撞、等温变化、等幅振荡等；描述状态的有：热学中的平衡状态、电学中的静电平衡等；描述器件的有：如单摆、理想电表、理想变压器等……)，再对模型进行研究，得出有关的定义、概念、规律等知识，最后用这些规律性的知识去解决问题，这就是中学物理研究问题的基本方法。

即从实际问题分析总结得出模型研究得出规律运用解决实际问题。

因此，在解决实际问题时，能否全面的掌握已经学过的模型（条件、范围、意义等）,是否能从问题所设定的情境中恰当地确认模型、正确地建立模型、熟练地应用模型是解决问题的关键。

物理学中杆是很常见的。

由于杆在实际中往往起到传递力和力矩的作用，它受到的可能是压力、拉力，有时可能是切力。

其方向可能沿杆的方向，也可能和杆有一定的夹角。

正是因为这样，实际中在没有明确给出杆的质量的情况下，我们通常将杆简化为：没有质量，不考虑粗细及形变的轻质细杆，即轻质细杆模型。

但实际问题是复杂的，在有些情况下只能将杆简化为：没有质量、没有形变，但必须考虑粗细的轻质粗杆，即轻质粗杆模型。

对杆的这两种模型来说，无论杆受力怎样，运动状态如何，总有：其合力为零；力矩的代数和为零，这是分析轻质杆受力问题的依据。

现举例分析两种模型的应用。

例1．小车上有轻质杆支架，B端固定一质量为m的小球，ADC端为铰链，D为AB的中点，CB 两点在同一水平线上，如图1所示，则1）当小车静止时，球和CD杆对AB杆的作用力各多大？2）当小车以加速度a向左运动时，球和CD杆对AB杆的作用力又怎样？分析：1）当小车静止时，系统平衡，要分析小球和CD杆对AB杆的作用力，必须先分析小球和CD杆的受力情况。

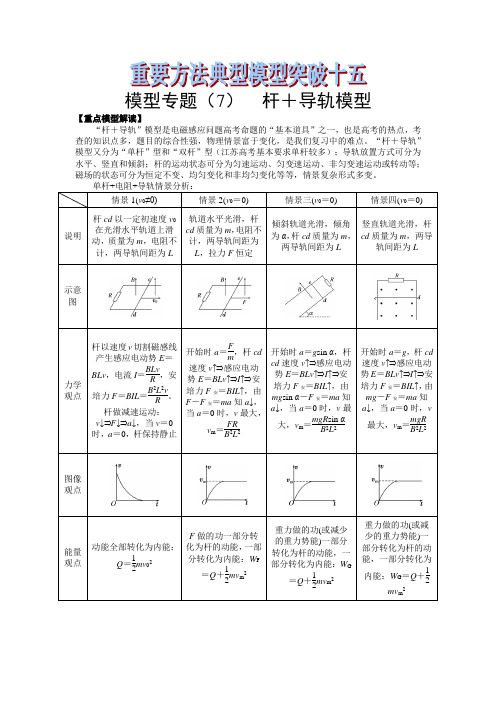
模型专题（7）杆＋导轨模型【重点模型解读】“杆＋导轨”模型是电磁感应问题高考命题的“基本道具”之一，也是高考的热点，考查的知识点多，题目的综合性强，物理情景富于变化，是我们复习中的难点。

“杆＋导轨”模型又分为“单杆”型和“双杆”型（江苏高考基本要求单杆较多）；导轨放置方式可分为水平、竖直和倾斜；杆的运动状态可分为匀速运动、匀变速运动、非匀变速运动或转动等；磁场的状态可分为恒定不变、均匀变化和非均匀变化等等，情景复杂形式多变。

情景1(v0≠0)情景2(v0＝0)情景三(v0＝0)情景四(v0＝0)说明杆cd以一定初速度v0在光滑水平轨道上滑动，质量为m，电阻不计，两导轨间距为L轨道水平光滑，杆cd质量为m，电阻不计，两导轨间距为L，拉力F恒定倾斜轨道光滑，倾角为α，杆cd质量为m，两导轨间距为L竖直轨道光滑，杆cd质量为m，两导轨间距为L示意图力学观点杆以速度v切割磁感线产生感应电动势E＝BLv，电流I＝BLvR，安培力F＝BIL＝B2L2vR。

杆做减速运动：v↓⇒F↓⇒a↓，当v＝0时，a＝0，杆保持静止开始时a＝Fm，杆cd速度v↑⇒感应电动势E＝BLv↑⇒I↑⇒安培力F安＝BIL↑，由F－F安＝ma知a↓，当a＝0时，v最大，v m＝FRB2L2开始时a＝g sin α，杆cd速度v↑⇒感应电动势E＝BLv↑⇒I↑⇒安培力F安＝BIL↑，由mg sin α－F安＝ma知a↓，当a＝0时，v最大，v m＝mgR sin αB2L2开始时a＝g，杆cd速度v↑⇒感应电动势E＝BLv↑⇒I↑⇒安培力F安＝BIL↑，由mg－F安＝ma知a↓，当a＝0时，v最大，v m＝mgRB2L2图像观点能量观点动能全部转化为内能：Q＝12mv02F做的功一部分转化为杆的动能，一部分转化为内能：W F＝Q＋12mv m2重力做的功(或减少的重力势能)一部分转化为杆的动能，一部分转化为内能：W G＝Q＋12mv m2重力做的功(或减少的重力势能)一部分转化为杆的动能，一部分转化为内能：W G＝Q＋12mv m2情景1(v0＝0)情景2(v0＝0)情景3(v0＝0)情景4(v0＝0)说明轨道水平光滑，杆cd质量为m，电阻不计，两导轨间距为L轨道水平光滑，杆cd质量为m，电阻不计，两导轨间距为L，拉力F恒定倾斜轨道光滑，杆cd质量为m，电阻不计，两导轨间距为L竖直轨道光滑，杆cd质量为m，电阻为R，两导轨间距为L示意图力学观点S闭合，杆cd受安培力F＝BLEr，a＝BLEmr，杆cd速度v↑⇒感应电动势E感＝BLv↑⇒I↓⇒安培力F＝BIL↓⇒加速度a↓，当E感＝E时，v最大，且v m＝EBL开始时a＝Fm，杆cd速度v↑⇒E＝BLv↑，经过Δt速度为v＋Δv，E′＝BL(v＋Δv)，Δq＝C(E′－E)＝CBLΔv，I＝ΔqΔt＝CBLa，F安＝CB2L2a，a＝Fm＋B2L2C，所以杆匀加速运动开始时a＝g sinα，杆cd速度v↑⇒E＝BLv↑，经过Δt速度为v＋Δv，E′＝BL(v＋Δv)，Δq＝C(E′－E)＝CBLΔv，I＝ΔqΔt＝CBLa，F安＝CB2L2a，mg sin α－F安＝ma，a＝mg sin αm＋CB2L2，所以杆匀加速运动开始时a＝g，杆cd速度v↑⇒E＝BLv↑，经过Δt速度为v＋Δv，E′＝BL(v＋Δv)，Δq＝C(E′－E)＝CBLΔv，I＝ΔqΔt＝CBLa，F安＝CB2L2a，mg－F安＝ma，a＝mgm＋CB2L2，所以杆匀加速运动图像观点能量观点电源输出的电能转化为动能：W电＝12mv m2F做的功一部分转化为动能，一部分转化为电场能：W F＝12mv2＋E C重力做的功一部分转化为动能，一部分转化为电场能：W G＝12mv2＋E C重力做的功一部分转化为动能，一部分转化为电场能：W G＝12mv2＋E C【例1】如图所示，间距L=1.0m的固定平行光滑金属导轨平面与水平面成θ=37°角，导轨上端接有阻值为R=1.0Ω的电阻，整个装置处在磁感应强度大小为B=1.0T，方向垂直于导轨平面向下的匀强磁场中。

2.常见双杆情景及解题思路常见情景(以水平光滑导轨为例) 过程分析三大观点的应用双杆切割式杆MN做变减速运动，杆PQ做变加速运动，稳定时，两杆的加速度均为零，以相同的速度匀速运动，对系统动量守恒，对其中某杆适用动量定理动力学观点：求加速度能量观点：求焦耳热动量观点：整体动量守恒求末速度，单杆动量定理求冲量、电荷量不等距导轨杆MN做变减速运动，杆PQ做变加速运动，稳定时，两杆的加速度均为零，两杆以不同的速度做匀速运动，所围的面积不变，v1L1＝v2L2动力学观点：求加速度能量观点：求焦耳热动量观点：动量不守恒，可分别用动量定理联立末速度关系求末速度双杆切割式a PQ减小，a MN增大，当a PQ＝a MN时二者一起匀加速运动，存在稳定的速度差动力学观点：分别隔离两导体棒， F－B2L2△vR总＝m PQ a，B2L2△vR总＝m MN a，求加速度1.如图所示，宽为L的两固定足够长光滑金属导轨水平放置，空间存在竖直向上的匀强磁场，磁感应强度大小为B。

质量均为m、电阻值均为r的两导体棒ab和cd静止置于导轨上，其间距也为L，现给cd一向右的初速度v0，对它们之后的整个运动过程说法正确的是( )A.ab的加速度越来越大，cd的加速度越来越小B.cd克服安培力所做的总功为14mv2C.通过ab的电荷量为mv02BLD.两导体棒间的距离最终变为L+mv0rB2L22.竖直放置的平行光滑导轨，其电阻不计，磁场方向如图所示，磁感应强度B=0.5T，导体杆ab和cd的长均为0.2m，电阻均为0.1Ω，所受重力均为0.1N，现在用力向上推导体杆ab，使之匀速上升(与导轨接触始终良好)，此时cd恰好静止不动，ab上升时下列说法正确的是( )A.ab受到的推力大小为2NB.ab向上的速度为2m/sC.在2s内，推力做功转化的电能是0.4JD.在2s内，推力做功为0.6J3.如图所示，相距为L 的两条足够长的平行金属导轨右端连接有一定值电阻R ，整个装置被固定在水平地面上，整个空间存在垂直于导轨平面向下的匀强磁场，磁感应强度大小为B ，两根质量均为m ，电阻都为R ，与导轨间的动摩擦因数都为μ的相同金属棒MN 、EF 垂直放在导轨上。

杆模型知识点总结一、概念杆模型是指在力学中用于研究棒状物体受力情况的一种模型。

在杆模型中，棒状物体通常被视为无质量、无弹性的理想化对象，用来分析棒状物体在受外力作用下的受力情况和运动规律。

杆模型是力学学科中的一个重要概念，广泛应用于工程技术、物理学、工业设计、建筑等领域。

二、杆模型的基本属性1. 无质量在杆模型中，棒状物体通常被假设为无质量的对象。

这是为了简化问题的分析，将物体的质量对力学分析的影响忽略掉。

由于棒状物体的质量与受力情况并无直接的关系，因此可以将棒状物体视为无质量的理想化对象。

2. 刚性杆模型中的物体通常被视为刚体，即在受力情况下不发生形变的物体。

这是为了使问题的分析更加简化，忽略掉物体的变形对受力情况的影响。

在杆模型中，通常假设棒状物体是刚性的，使得分析更为方便。

3. 无弹性在杆模型中，棒状物体通常被假设为无弹性的。

这意味着在受到外力作用后，棒状物体不会发生形变或者变形极小，忽略掉物体的变形对受力情况的影响。

这样假设可以使问题的分析更加简化，减少了变形引起的复杂计算。

三、杆模型的应用1. 物体受力分析杆模型广泛应用于物体受力分析的问题中。

通过建立杆模型，可以便于分析物体受力的情况，包括受到的外力和支持反力等。

利用杆模型，可以清晰地了解物体受力的方向和大小，从而进行有效的受力分析。

2. 结构设计在工程技术和建筑领域中，杆模型常常用于结构设计中。

通过建立杆模型，可以对结构的受力情况进行分析和计算，以确保结构在受力情况下能够满足设计要求，保证结构的稳定和安全。

3. 力的传递杆模型在力的传递问题中也有着重要的应用。

通过建立杆模型，可以分析和计算力的传递过程，包括力的大小、方向和传递路径等。

通过杆模型的分析，可以有效地设计和优化力的传递系统。

四、杆模型的基本原理1. 受力分析杆模型的基本原理之一是受力分析。

通过建立杆模型，可以清晰地了解物体受力的情况，包括受到的外力和支持反力等。

在受力分析过程中，可以利用受力平衡的原理，确定物体受力的方向和大小，实现对受力情况的全面分析。

第五章 杆系结构的有限元法 5.1 引言杆系结构是工程中应用较为广泛的结构体系，包括平面或空间形式的梁、桁架、刚架、拱等。

其组成形式虽然复杂多样，但用计算机进行分析时却较为简单。

杆系结构中的每个杆件都是一个明显的单元。

杆件的两个端点自然形成有限元法的节点，杆件与杆件之间则用节点相连接。

显然，只要建立起杆件两端位移与杆端力之间的关系，则整体平衡方程的建立与前几章完全相同。

杆端位移与杆端力之间的关系，可用多种方法建立，包括前面几章一直采用的虚功原理，但是采用材料力学、结构力学的某些结论，不仅物理概念清晰、直观，而且推导过程简单明了。

因此，本章将采用这种方法进行单元分析。

至于整体平衡方程的建立，则和前面几章所讲的方法一样，即借助于单位定位向量，利用单元集成法进行。

5.2 平面桁架的有限元分析平面桁架在计算上有以下几个特点： 1． 杆件的每个节点仅有两个线位移； 2． 杆件之间的连接为理想铰，即在节点处各杆件可相对自由转动，且杆件轴线交于一点。

3． 外载荷均为作用于节点的集中力。

由于以上特点，所以在理论上各杆件只产生轴向拉、压力，截面应力分布均匀，材料可得到充分利用，因此桁架结构往往用于大跨结构。

5.2.1 局部坐标系下的单元刚度矩阵从平面桁架中任取一根杆件作为单元，称作桁架单元，单元长为L ，横截面面积为A ，图5.1。

两端节点分别用i 和j 表示，规定从i 到j 的连线方向为局部坐标x 轴，垂直于x 的方向为y 轴。

图5.1由于桁架中各杆只产生轴向力和轴向变形，所以节点i 和j 只发生沿x 方向的位移，用i u 和j u 表示，相应的杆端轴力分别用xi F 和xj F 表示。

由虎克定律可推得)()()(j i i j xj j i xi u u L EA u u L EA F u u LEAF --=-=-=将这两个式子写成矩阵形式，就是e j i exj xi u u L EA LEA L EA L EA F F ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧ (5.1)显然，在局部坐标系下，i 、j 两节点沿y 轴方向的位移0==j i v v ，在y 轴方向的节点力0==yj yi F F 。

轻绳模型、轻杆模型和轻弹簧模型建议用时：50分钟考点序号考点题型分布考点1轻绳模型10单选考点2轻杆模型7单选考点3轻弹簧模型4单选+3多选考点01：轻绳模型(10单选)一、单选题1(2023·甘肃·统考一模)如图所示，一轻绳的一端系在竖直墙上M点，轻绳穿过一轻质光滑圆环O，另一端系一质量为m的物体A。

现用力F拉住轻环上一点，使物体A从图中虚线位置缓慢上升到实线位置。

则在此过程中，绳中张力F T、力F和力F与水平方向夹角θ的变化情况正确的是()A.F T保持不变，F保持不变，夹角θ逐渐减小B.F T保持不变，F逐渐增大，夹角θ逐渐增大C.F T逐渐增大，F逐渐减小，夹角θ逐渐减小D.F T逐渐减小，F保持不变，夹角θ逐渐增大【答案】B【详解】F T等于物体A的重力，故保持不变；因为圆环两边绳子的拉力相等，故当物体A从图中虚线位置缓慢上升到实线位置时，两边绳子的夹角减小，由力的合成知识可知，两边绳子的合力变大，即F变大；因F 的方向总是在两边绳子夹角的平分线向上的方向，故当物体A从图中虚线位置缓慢上升到实线位置时，夹角θ逐渐增大。

故选B。

2(2023·全国·高三专题练习)如图所示，光滑半圆形轨道MAN固定在竖直平面内，MN为水平直径，一轻质小环A套在轨道上，轻绳一端固定在M点，另一端穿过小环系一质量为m的小球恰好静止在图示位置，不计所有摩擦，重力加速度大小为g。

下列说法正确的是()mg B.轻绳对M点拉力的大小为2mgA.轻绳对M点拉力的大小为32C.轻绳对小环A作用力的大小为3mgD.轻绳对小环A作用力的大小为2mg【答案】C【分析】本题考查共点力的平衡，从重物端开始受力分析，得到绳上的力后对轻环受力分析即可。

【详解】AB．因为小球恰好静止，绳上拉力等于小球重力，轻绳上拉力处处相等，轻绳对M点的拉力为mg，所以AB错误；CD．轻环受轻绳的两股力以及轨道的支持力共三个力而平衡，绳上的两股力的合力与环的支持力等大反向，所以绳的合力沿AO方向，又绳上的力相等，所以AO是两股绳夹角的角平分线，所以∠OAM=30°，所以合力F=2mg cos30°=3mg，所以C正确，D错误。

绳(杆)端速度分解模型1．模型特点沿绳(杆)方向的速度分量大小相等． 2．思路与方法合速度→绳(杆)拉物体的实际运动速度v分速度→⎩⎪⎨⎪⎧其一：沿绳(杆)的速度v 1其二：与绳(杆)垂直的分速度v 2方法：v 1与v 2的合成遵循平行四边形定则． 3．解题的原则把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相等求解．常见的模型如图7所示．关联体：通过绳子、轻杆或者其他之间联系的两个相互作用的物体 【核心方法点拨】(1)如果物体是通过杆或者绳子关联，由于高中研究的绳都是不可伸长的，杆都是不可伸长和压缩的，即绳或杆的长度不会改变，所以解题的原则是：把物体的实际速度分解为垂直于绳(或杆)和平行于绳(或杆)的两个分量，根据沿绳(杆)方向的分速度大小相同求解．(2)若两物体是通过接触面接触的，则将物体的实际速度沿平行与垂直接触面方向进行分解，在垂直接触面方向上速度相等题型一 通过轻绳关联1．（2021·安徽·定远县育才学校高一阶段练习）如图所示，物体A 和B 的质量均为m ，分别与跨过定滑轮的轻绳连接（不计绳与滑轮、滑轮与轴之间的摩擦）。

现用水平变力F 拉着物体A 沿水平方向向右做匀速直线运动。

则下列说法中正确的是（ ）A ．物体B 做匀速直线运动 B ．物体B 做加速直线运动C ．绳子对物体B 的拉力等于mgD ．绳子对物体B 的拉力小于mg2．（2021·河南·濮阳南乐一高高二开学考试）如图所示，已知m A =3m B ，C 为内壁光滑、半径为R 的半圆形轨道，D 为定滑轮，开始时A 、B 均处于静止状态，释放后，A 沿圆弧轨道下滑，若已知A 球下滑到最低点时的速度为v ，则此时B 的速度为（ ）A vB ．12v C v D ．2v3．（2022·广东高州·高一期末）如图所示绳子通过固定在天花板上的定滑轮，左端与套在固定竖直杆上的物体A 连接，右端与放在水平面上的物体B 相连，到达如图所示位置时，绳与水平面的夹角分别为夹角为37︒、53︒，两物体的速率分别为A v 、B v ，且此时20m /s 3+=A B v v ，3sin 375︒=、4cos375︒=，则A v 的大小为（ ）A ．10m/s 3 B ．4m/s 3C ．2m/sD ．4m/s4．（多选）（2022·山东·威海市教育教学研究中心高一期末）如图所示，不可伸长的轻绳绕过光滑定滑轮C 与物体A 连接，绳的另一端和套在固定竖直杆上的物体B 连接，开始时，BC 连线沿水平方向。