浙江大学高级数据结构课件
- 格式:ppt
- 大小:719.00 KB
- 文档页数:18

数据结构的定义数据结构是计算机中存储、组织数据的方式,它定义了数据元素之间的逻辑关系以及如何在计算机中表示这些关系。
提高算法效率合适的数据结构可以显著提高算法的执行效率,降低时间复杂度和空间复杂度。
简化程序设计数据结构为程序设计提供了统一的抽象层,使得程序员可以更加专注于问题本身,而不是底层的数据表示和访问细节。
便于数据管理和维护良好的数据结构设计可以使得数据的管理和维护变得更加方便和高效。
数据结构的定义与重要性线性数据结构中的元素之间存在一对一的关系,如数组、链表、栈和队列等。
线性数据结构非线性数据结构中的元素之间存在一对多或多对多的关系,如树、图等。
非线性数据结构静态数据结构在程序运行期间不会发生改变,如数组、静态链表等。
静态数据结构动态数据结构在程序运行期间可以动态地添加或删除元素,如链表、动态数组等。
动态数据结构数据结构的分类01020304在计算机科学中,数据结构是算法设计和分析的基础,广泛应用于操作系统、编译原理、数据库等领域。
计算机科学在软件工程中,数据结构是软件设计和开发的重要组成部分,用于实现各种软件功能和性能优化。
软件工程在人工智能中,数据结构用于表示和处理各种复杂的数据和知识,如神经网络、决策树等。
人工智能在大数据处理中,数据结构用于高效地存储、管理和分析海量数据,如分布式文件系统、NoSQL 数据库等。
大数据处理数据结构的应用领域0102线性表是具有n个数据元素的有限序列创建、销毁、清空、判空、求长度、获取元素、修改元素、插入元素、删除元素等线性表的定义线性表的基本操作线性表的定义与基本操作03用一段地址连续的存储单元依次存储线性表的数据元素顺序存储结构的定义可以随机存取,即可以直接通过下标访问任意元素;存储密度高,每个节点只存储数据元素顺序存储结构的优点插入和删除操作需要移动大量元素;空间利用率不高,需要提前分配存储空间顺序存储结构的缺点链式存储结构的定义01用一组任意的存储单元存储线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的链式存储结构的优点02插入和删除操作不需要移动大量元素,只需要修改指针;空间利用率高,不需要提前分配存储空间链式存储结构的缺点03不能随机存取,只能通过从头节点开始遍历的方式访问元素;存储密度低,每个节点除了存储数据元素外,还需要存储指向下一个节点的指针0102定义栈(Stack)是一种特殊的线性数据结构,其操作只能在一端(称为栈顶)进行,遵循后进先出(LIFO)的原则。



高级数据结构和算法分析Advanced Data Structures and Algorithm Analysis主讲教师:陈越Instructor: CHEN, YUEE-mail: chenyue@ Courseware and homework sets can be downloaded from /dsaa/教材(Text Book)Data Structures andAlgorithm Analysis in C(2nd Edition)Mark Allen Weiss陈越改编Email: weiss@参考书目(Reference)数据结构与算法分析(C语言版)魏宝刚、陈越、王申康编著浙江大学出版社 Data Structures, Algorithms, and Applications in C++数据结构算法与应用——C++语言描述(英文版)Sartaj Sahni McGraw-Hill & 机械工业出版社 数据结构课程设计何钦铭、冯雁、陈越著浙江大学出版社课程评分方法(Grading Policies)Research Project (23 or 25)Discussions(14)Homework (5)Q&A (0.5 each)Total 45Final Exam (55)Discussions(14)Form groups of 3 or 428 in-class discussion topicsEach takes 3~5 minutes14 = 28 10 / 20Research topics (23 or 25)◆Done in groups◆16 topics to choose from◆Report (18 or 20 points)◆In-class presentation (5~10 minutes, 5 points)◆The speaker will be chosen randomly from all thecontributors◆If there are many volunteers, only one group willbe chosen◆If there is no volunteer, I will talk about itHomework (5)✓Done independently✓10 problems✓Collected before the end of the next class meeting ✓ 5 = 10 10 / 20✓Late penalty: 2 points/weekQ&A⏹For volunteers only⏹0.5 point for each question asked/answered ⏹come and claim your credits after each classsession。




浙江大学精品课程一、课程介绍浙江大学是中国一所著名的高等学府,拥有较长的历史和丰富的教学资源。
作为一所综合性大学,浙江大学开设了许多精品课程,涵盖了各个学科领域。
这些精品课程以其教学质量和教学内容的丰富性而受到广大学生的欢迎和推崇。
二、精品课程列表下面介绍几门浙江大学的精品课程:1. 数据结构与算法(C++版)•课程代码:CS001•学分:3•课程简介:数据结构与算法是计算机科学与技术专业中非常重要的一门基础课程。
这门课程主要介绍了常用的数据结构和算法设计与分析的基本原则。
通过学习这门课程,学生能够掌握常见数据结构的实现原理和应用场景,并具备设计和分析算法的能力。
•课程特点:该课程采用C++语言作为主要教学工具,综合了数据结构和算法的理论讲解和实践操作。
课程中会有大量的编程练习和实验,帮助学生更好地掌握课程所涵盖的知识。
2. 中国特色社会主义理论与实践•课程代码:PHI001•学分:2•课程简介:中国特色社会主义理论与实践是一门探讨中国特色社会主义制度和道路的重要课程。
通过本课程的学习,学生可以了解中国特色社会主义理论的源起、发展及实践,掌握充满中国特色的社会主义理论体系。
•课程特点:该课程以理论与实践相结合为特点,旨在帮助学生理解中国特色社会主义的本质和特点。
课程内容包括中国特色社会主义理论的基本概念、核心价值观、政治制度和改革开放等方面的详细介绍。
3. 人工智能导论•课程代码:CS002•学分:3•课程简介:人工智能导论是一门介绍人工智能领域基本知识和技术的课程。
通过本课程的学习,学生可以了解人工智能的基本概念、发展历程、应用领域和相关技术,培养学生在人工智能领域的基本能力和创新思维。
•课程特点:该课程内容包括人工智能的基本概念、智能代理、知识表示与推理、机器学习、自然语言处理等方面的内容。
课程采用理论讲解、实践操作和案例分析相结合的方式,加深学生对人工智能概念和技术的理解。
4. 创新创业与科技管理•课程代码:ECO001•学分:3•课程简介:创新创业与科技管理是一门介绍创新创业与科技管理理论和实践的课程。

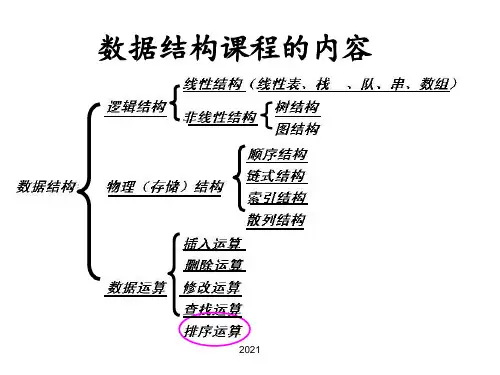
“数据结构知识导入全程目标•数据结构的基本概念–逻辑结构–物理结构–运算结构•数据结构的基本实现–堆栈–队列–链表–二叉树知识讲解数据结构的基本概念•数据结构是相互之间存在一种或多种特定关系的数据的集合•数据结构是计算机存储、组织数据的方式•数据结构的选择直接影响计算机程序的运行效率(时间复杂度)和存储效率(空间复杂度)•计算机程序设计=算法+数据结构•数据结构的三个层次–抽象层——逻辑结构–结构层——物理结构–实现层——运算结构识讲解•集合结构(集)–结构中的数据元素除了同属于一个集合外没有其它关系识讲解•线性结构(表)–结构中的数据元素具有一对一的前后关系识讲解•树型结构(树)–结构中的数据元素具有一对多的父子关系知识讲解实现双向线性链表•删除节点识讲解•树形结构的最简模型,每个节点最多有两个子节点•每个子节点有且仅有一个父节点,整棵树只有一个根节点•具有递归的结构特征,用递归的方法处理,可以简化算法•三种遍历序–前序遍历:D-L-R–中序遍历:L-D-R–后序遍历:L-R-D识讲解•二叉树的一般形式–根节点、枝节点和叶节点–父节点和子节点–左子节点和右子节点–左子树和右子树–大小和高度(深度)识讲解•满二叉树–每层节点数均达到最大值–所有枝节点均有左右子树知识讲解二叉树•完全二叉树–除最下层外,各层节点数均达到最大值–最下层的节点都连续集中在左边识讲解•顺序存储–从上到下、从左到右,依次存放–非完全二叉树需用虚节点补成完全二叉树识讲解•链式存储–二叉链表,每个节点包括三个域,一个数据域和两个分别指向其左右子节点的指针域识讲解•链式存储–三叉链表,每个节点包括四个域,一个数据域、两个分别指向其左右子节点的指针域和一个指向其父节点的指针域知识讲解实现有序二叉树•有序二叉树亦称二叉搜索树,若非空树则满足:–若左子树非空,则左子树上所有节点的值均小于等于根节点的值–若右子树非空,则右子树上所有节点的值均大于等于根节点的值–左右子树亦分别为有序二叉树•基于有序二叉树的排序和查找,可获得O(logN)级的平均时间复杂度知识讲解逻辑结构•网状结构(图)–结构中的数据元素具有多对多的交叉映射关系识讲解•顺序结构–结构中的数据元素存放在一段连续的地址空间中识讲解•顺序结构–随机访问方便,空间利用率低,插入删除不方便识讲解•链式结构–结构中的数据元素存放在彼此独立的地址空间中–每个独立的地址空间称为节点–节点除保存数据外,还需要保存相关节点的地址识讲解•链式结构–插入删除方便,空间利用率高,随机访问不方便知识讲解逻辑结构与物理结构的关系•每种逻辑结构采用何种物理结构实现,并没有一定之规,通常根据实现的难易程度,以及在时间和空间复杂度方面的要求,选择最适合的物理结构,亦不排除复合多种物理结构实现一种逻辑结构的可能知识讲解运算结构•创建与销毁–分配资源、建立结构、释放资源•插入与删除–增加、减少数据元素•获取与修改–遍历、迭代、随机访问•排序与查找–算法应用知识讲解数据结构的基本实现•堆栈–基于顺序表的实现–基于链式表的实现•队列–基于顺序表的实现–基于链式表的实现•链表–双向线性链表的实现•二叉树–有序二叉树(二叉搜索树)的实现知识讲解堆栈•后进(压入/push)先出(弹出/pop)识讲解•初始化空间、栈顶指针、判空判满识讲解•动态分配、栈顶指针、注意判空知识讲解队列•先进(压入/push)先出(弹出/pop)识讲解•初始化空间、前弹后压、循环使用、判空判满识讲解•动态分配、前后指针、注意判空知识讲解链表•地址不连续的节点序列,彼此通过指针相互连接•根据不同的结构特征,将链表分为:–单向线性链表–单向循环链表–双向线性链表–双线循环链表–数组链表–链表数组–二维链表识讲解•单向线性链表识讲解•单向循环链表识讲解•双向线性链表识讲解•双向循环链表识讲解•数组链表识讲解•链表数组识讲解•二维链表识讲解•结构模型识讲解•插入节点。

数据结构-链表实现多项式求和浙江⼤学数据结构课程第⼆讲练习:使⽤链表实现多项式求和与乘积,只写了求和,乘积暂时没写。
#include <iostream>#include <stdio.h>using namespace std;//Polynomial是typedef为PolyNode *类型声明的别名typedef struct PolyNode *Polynomial;struct PolyNode{int coef;int expon;Polynomial link;};void Attach(int c, int e, Polynomial *pRear) /* *pRear是指向指针的指针,这⾥是为了按值传递从⽽改变Rear的值 */{Polynomial P;P = (Polynomial)malloc(sizeof(struct PolyNode)); /*创建新节点,⽤于存储当前多项式*/P->link = NULL; /*因为插⼊每次的节点都是链表尾,所以要使其指针指向NULL*/P->coef = c; /*为新节点赋值*/P->expon = e;(*pRear)->link = P;*pRear = P; /*----------------改变Rear指向当前链表结尾-----------------*/}Polynomial ReadPoly(){Polynomial P,t;Polynomial Rear; /*当前结果表达式尾项指针*/int c, e, N;scanf("%d", &N); /*读⼊多项式总共有⼏项*/P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL; /*采⽤申请空节点作为链表头*/Rear = P; /*将当前节点的指针赋予Rear*/if (N < 1) /*检查数据是否输⼊正确*/cout << "input is error" << endl;while (N--) {scanf("%d %d", &c, &e); /*读⼊多项式的系数和指数*/Attach(c, e, &Rear); /*将当前项插⼊多项式*/}t = P; P = P->link; free(t); /*释放⼀开始申请的空节点*//*.................*/return P;}Polynomial Add(Polynomial P1, Polynomial P2){Polynomial t1, t2, P;Polynomial Rear;t1 = P1; t2 = P2; /*P1和P2指向表头,不能改变它的值,否则找不到链表*/P = (Polynomial)malloc(sizeof(struct PolyNode)); P->link = NULL; /*采⽤申请空节点作为链表头*/Rear = P;while (t1&&t2) {if (t1->expon == t2->expon) {if ((t1->coef + t2->coef) != 0){Attach(t1->coef + t2->coef, t1->expon, &Rear);t1 = t1->link;t2 = t2->link;}else {t1 = t1->link;t2 = t2->link;}}else if (t1->expon > t2->expon) {Attach(t1->coef, t1->expon, &Rear);t1 = t1->link;}else {Attach(t2->coef, t2->expon, &Rear);t2 = t2->link;}}while (t1) {Attach(t1->coef, t1->expon, &Rear);t1 = t1->link;}while (t2){Attach(t2->coef, t2->expon, &Rear);t2 = t2->link;}Polynomial t;t = P; P = P->link; free(t);return P;}void PrintPoly(Polynomial P){int flag = 0;if (!P) { printf("0 0\n"); return; }while (P){if (!flag)flag = 1;elseprintf("");printf("%d %d", P->coef, P->expon);P = P->link;}printf("\n");}int main(){Polynomial P1, P2, P;P1 = ReadPoly();P2 = ReadPoly();P = Add(P1, P2);//Polynomial t; /*释放表头(为啥表头的空节点会没有释放)*///t = P; P = P->link; free(t);PrintPoly(P);printf("%d %d", P->coef, P->expon);return0;}总结:1.表头的指针不能动,否则会找不到链表的⼊⼝2.申请空节点作为表头时,插⼊数据后要把该节点的内存释放(free)3.使⽤malloc申请内存 百度百科:申请⼀块连续的指定⼤⼩的内存块区域以void*类型返回分配的内存区域地址,当⽆法知道内存具体位置的时候,想要绑定真正的内存空间,就需要⽤到动态的分配内存 ⽤法举例:P = (Polynomial)malloc(sizeof(struct PolyNode)); //Polynomial是struct PolyNode*的typeof别名,P就是这块节点在内存⾥的存储位置4.关于链表的指针域,存放的是指针,该指针⼀般指向链表下⼀个节点的存储位置 P1 = (Polynomial)malloc(sizeof(struct PolyNode)); ⽐如P是当前节点,申请了P1节点后,令P->link = P1,即实现了为链表插⼊新节点。
高级数据结构在计算机科学的广袤领域中,数据结构就如同是构建高楼大厦的基石,为各种算法和程序提供了坚实的支撑。
而高级数据结构,则是在基础数据结构之上发展而来,具有更复杂的特性和更强大的功能,能够应对更加复杂和多样化的计算问题。
让我们先来谈谈什么是数据结构。
简单来说,数据结构就是数据的组织方式,它决定了数据的存储、访问和操作方式。
常见的基础数据结构包括数组、链表、栈、队列等。
数组是一种连续存储的线性结构,通过索引可以快速访问元素;链表则是通过节点之间的链接来存储数据,适合频繁的插入和删除操作;栈遵循“后进先出”的原则,常用于函数调用和表达式求值;队列则是“先进先出”,在任务调度等场景中发挥着重要作用。
然而,当面对一些复杂的问题时,基础数据结构可能就显得力不从心了,这时候就需要高级数据结构登场。
其中,树结构是一种非常重要的高级数据结构。
二叉树是树结构中的常见类型,它的每个节点最多有两个子节点。
二叉搜索树则是在二叉树的基础上,具有特定的节点排列规则,使得对于任意节点,其左子树中的所有节点值都小于该节点值,右子树中的所有节点值都大于该节点值。
这一特性使得在二叉搜索树中进行查找、插入和删除操作的平均时间复杂度为 O(log n),大大提高了效率。
除了二叉树,还有 AVL 树、红黑树等平衡二叉树。
它们通过自动调整树的结构,保持树的高度平衡,从而保证了操作的高效性。
AVL树通过严格的平衡条件,使得树的左右子树高度差最多为 1;红黑树则相对宽松一些,但同样能够保证在最坏情况下的操作性能。
堆也是一种特殊的树结构,常见的有最大堆和最小堆。
最大堆中,每个节点的值都大于或等于其子节点的值;最小堆则相反。
堆常用于实现优先队列,能够快速获取最大或最小元素。
另一种重要的高级数据结构是图。
图可以用来表示各种复杂的关系,例如社交网络中的人际关系、交通网络中的道路连接等。
图的存储方式有邻接矩阵和邻接表两种。
在图的算法中,深度优先搜索和广度优先搜索是常用的遍历算法,用于访问图中的所有节点。