电工学-第二章习题答案
- 格式:ppt
- 大小:2.15 MB
- 文档页数:64
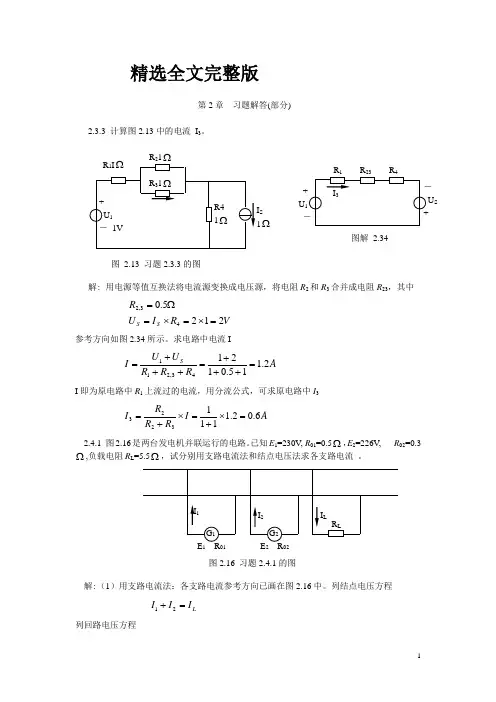
精选全文完整版第2章 习题解答(部分)2.3.3 计算图2.13中的电流 I 3。
解: 用电源等值互换法将电流源变换成电压源,将电阻R 2和R 3合并成电阻R 23,其中 V R I U R S S 2125.043,2=⨯=⨯=Ω=参考方向如图2.34所示。
求电路中电流IA R R R U U I S 2.115.012143,211=+++=+++= I 即为原电路中R 1上流过的电流,用分流公式,可求原电路中I 3A I R R R I 6.02.11113223=⨯+=⨯+= 2.4.1 图2.16是两台发电机并联运行的电路。
已知E 1=230V , R 01=0.5Ω,E 2=226V , R 02=0.3 Ω,负载电阻R L =5.5Ω,试分别用支路电流法和结点电压法求各支路电流 。
解:(1)用支路电流法:各支路电流参考方向已画在图2.16中。
列结点电压方程 L I I I =+21列回路电压方程S Ω 图 2.13 习题2.3.3的图U S U 图解 2.34101202图2.16 习题2.4.1的图L L 0222LL 0111R I R I E R I R I E +=+=联立求解上述三各方程式组成的方程组,可得A 40A2021===L I I I验算:按非独立回路方程进行02201121R I R I E E -=-代入数据443.0205.020226230==⨯-⨯=- (正确!)(2)用结点电压法求解:先求端电压U ,有V 2205.513.015.013.02265.02301110201022011=+++=+++=L R R R R E R E U A 405.0220A 205.0220226A 205.022023002220111====-=-==-=-=L L R U I R U E I R U E I 结果与上相同。
2.5.1 试用结点电压法求图2.18所示电路中的各支路电流解:在原图2.18中用O 和O ’标明两个结点,则有A 5.0505025V 505015015015025501005025a O ,O'-=-==++++=I U A 5.0505025A 15050100c b -=-==-=I I 2.6.1 用叠加原理计算图2.19中各支路的电流。
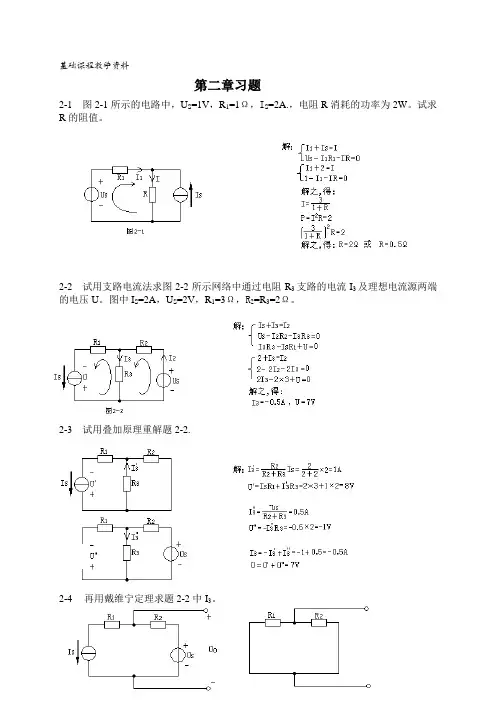
基础课程教学资料第二章习题2-1 图2-1所示的电路中,U S=1V,R1=1Ω,I S=2A.,电阻R消耗的功率为2W。
试求R的阻值。
2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。
图中I S=2A,U S=2V,R1=3Ω,R2=R3=2Ω。
2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。
2-5 图2-3所示电路中,已知U S1=6V,R1=2Ω,I S=5A,U S2=5V,R2=1Ω,求电流I。
2-6 图2-4所示电路中,U S1=30V,U S2=10V,U S3=20V,R1=5kΩ,R2=2kΩ,R3=10kΩ,I S=5mA。
求开关S在位置1和位置2两种情况下,电流I分别为多少?2-7 图2-5所示电路中,已知U AB=0,试用叠加原理求U S的值。
2-8 电路如图2-6所示,试用叠加原理求电流I。
2-9 电路如图2-7所示,试用叠加原理求电阻R4上电压U的表达式。
2-10电路如图2-8所示,已知R1=Ω,R2=R3=2Ω,U S=1V,欲使I=0,试用叠加原理确定电流源I S的值。
2-11 画出图2-9所示电路的戴维宁等效电路。
2-12 图2-10所示的电路接线性负载时,U 的最大值和I的最大值分别是多少?2-13 电路如图2-11所示,假定电压表的内阻无穷大,电流表的内阻为零。
当开关S处于位置1时,电压表的读数为10V,当S处于位置2时,电流表的读数为5mA。
试问当S处于位置3SHI 4,电压表和电流表的读数各为多少?2-14 图2-12所示电路中,各电源的大小和方向均未知,只知每个电阻均为6Ω,又知当R=6Ω时,电流I=5A。
今欲使R支路电流I=3A,则R应该多大?2-15 图2-13所示电路中,N为线性有源二端网络,测得AB之间电压为9V,见图(a);若连接如图(b)所示,可测得电流I=1A。
现连接如图(c)所示形式,问电流I为多少?2-16 电路如图2-14所示,已知R1=5Ω时获得的功率最大,试问电阻R是多大?本章小结1、支路电流法是分析和计算电路的基本方法,适用于任何电路。

《电工学》作业答案第二章 2-9解:变换过程如图所示,解得I 4 = 2A 。
2-10解:对结点a 列KCL 方程1230I I I对左、右边的网孔列KVL 方程1122S1S20R I R I U U 2233S2S30R I R I U U将数据代入上述方程,联立求解方程组12312230124243204432120I I I I I I I解得1231A 5A 6A I I I ,, 2-11解:对结点a 和b 列KCL 方程13S1S223S2S300I I I I I I I I对回路abca 列KVL 方程22S 11330R I U R I R I将数据代入上述方程,联立求解方程组132321362023022420I I I I I I I解得1232A 1A 2A I I I ,,2-12 解:根据两个结点电路中结点电压方程的一般形式得S1S2S3123a 12312612346V 6V 111111346U U U R R R U R R R 电流I 3可用欧姆定律求得a S333612A 3A 6U U I R2-14解:(a)电路图; (b)电压源U S 单独作用的电路; (c)电流源I S 单独作用的电路电压源U S1单独作用时,将U S2短路,电路如 (b)所示S1123123321232312318A 3.6A 6336333.6A 1.2A 6363.6A 2.4A63U I R R R R R R I I R R R I I R R电压源U S2单独作用时,将U S1短路,电路如图 (c)所示S2213213312131321315A 2A 3362332A 1A3332A 1A33U I R R R R R R I I R R R I I R RU S 和I S 共同作用时111222333 3.61A 2.6A 1.22A 0.8A 2.41A 3.4A I I I I I I I I I 2-16解:(a)I S1单独作用的电路; (b)I S2单独作用的电路; (c)U S 单独作用的电路电流源I S1单独作用时,电路如 (a)所示2S12333A 1.8A 32R I I R R电流源I S2单独作用时,电路如 (b)所示3S22325A 2A 32R I I R R电压源U S2单独作用时,电路如 (c)所示S 2315A 3A 32U I R RI S1、I S1和U S 共同作用时1.823A 6.8A I I I I2-19 解:(a) 求开路电压的电路; (b)求除源电阻的电路; (c) 戴维南等效电路求开路电压的等效电路如 (a)所示。

电工学第二章习题一、填空题1. 两个均为40F μ的电容串联后总电容为 80 F μ,它们并联后的总电容为 20 F μ。
2. 表征正弦交流电振荡幅度的量是它的 最大值 ;表征正弦交流电随时间变化快慢程度的量是 角频率ω ;表征正弦交流电起始位置时的量称为它的 初相 。
三者称为正弦量的 三要素 。
3. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ;电感元件上任一瞬间的电压电流关系可以表示为dtdiLu =L ;电容元件上任一瞬间的电压电流关系可以表示为dtduCi =C 。
由上述三个关系式可得, 电阻 元件为即时元件; 电感 和 电容 元件为动态元件。
4. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 50Ω ,该电路为 容 性电路。
电路中吸收的有功功率为 750W ,吸收的无功功率又为 1000var 。
二、选择题1. 某正弦电压有效值为380V ,频率为50Hz ,计时始数值等于380V ,其瞬时值表达式为( B )A 、t u 314sin 380=V ;B 、)45314sin(537︒+=t u V ;C 、)90314sin(380︒+=t u V 。
2. 一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P/2,则正弦交流电源电压的最大值为( D ) A 、7.07V ; B 、5V ; C 、14V ; D 、10V 。
3. 提高供电电路的功率因数,下列说法正确的是( D )A 、减少了用电设备中无用的无功功率;B 、减少了用电设备的有功功率,提高了电源设备的容量;C 、可以节省电能;D 、可提高电源设备的利用率并减小输电线路中的功率损耗。
4. 已知)90314sin(101︒+=t i A ,︒+=30628sin(102t i )A ,则( C )A 、i1超前i260°;B 、i1滞后i260°;C 、相位差无法判断。

电工学-电工技术(艾永乐)课后答案第二章第二章 电阻电路的分析本章的主要任务是学习电阻电路的分析计算方法,并运用这些方法分析计算各种电阻电路中的电流、电压和功率。
本章基本要求1. 正确理解等效电路的概念,并利用等效变换化简电路。
2. 掌握电阻串、并联等效变换、电源的等效变换。
3. 电阻电路的分压公式和分流公式的应用。
4. 运用支路电流法和结点电压法分析计算电路。
5. 运用叠加定理分析计算电路。
6. 熟练应用戴维宁定理分析计算电路。
7. 应用戴维宁定理求解电路中负载电阻获得的最大功率。
8. 学会含有受控源电路的分析计算。
9. 了解非线性电阻电路的分析方法。
本章习题解析2-1 求习题2-1所示电路的等效电阻,并求电流I 5。
3Ω2Ω2Ω4Ω4Ω6Ω1ΩI 5 a+-3V b 3Ω2Ω2ΩΩ6Ω1ΩI 5a+-3V解:电路可等效为题解2-1图由题解2-1图,应用串并联等效变换得5.1)6//)12(2//2//(3ab =++=R Ω由分流公式3136********=⋅+++⋅+=ab R I A 2-2 题2-2图所示的为变阻器调节分压电路。
50=L R Ω,电源电压220=U V ,中间环节是变阻器。
变阻器的规格是100Ω 3A 。
今把它平题解2-1题2-1图分为4段,在图上用a 、b 、c 、d 、e 等点标出。
试求滑动触点分别在a 、b 、c 、d 四点是,负载和变阻器所通过的电流及负载电压,并就流过变阻器的电流与其额定电流比较来说明使用时的安全问题。
+-Ud ab c e L+-U L I L解:1)a 点: 0L =U 0L =I 2.2100220ea ea ===R U I A 2) c 点:75eq =R Ω 93.275220eq ec ===R U I A 47.121ec L ==I I A 5.73L =U V3) d 点:55eq =R Ω 455220eq ed ===R U I A 4.2L =I A 6.1da =I A 120L =U V4) e 点: 2.2100220ea ea ===R U I A 4.450220L ==I A 220L =U V 2-3 试求习题2-3ab 之间的输入电阻。
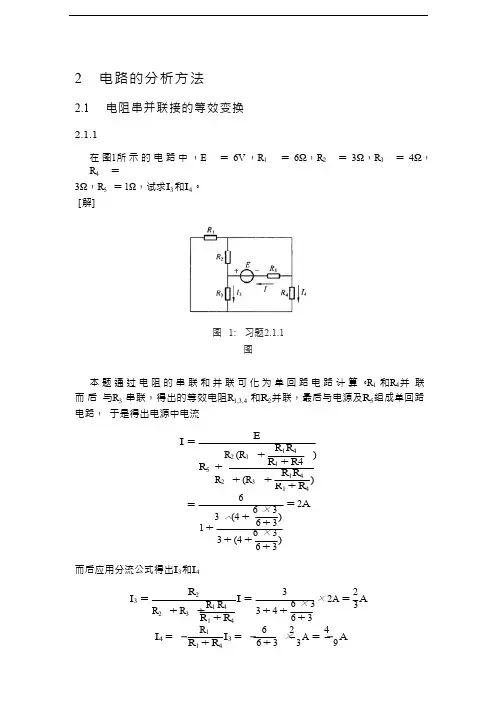
× R R R 2 电路的分析方法2.1 电阻串并联接的等效变换2.1.1在 图1所 示 的 电 路 中 ,E = 6V ,R 1 = 6Ω,R 2 = 3Ω,R 3 = 4Ω,R 4 =3Ω,R 5 = 1Ω,试求I 3 和I 4。
[解]图 1: 习题2.1.1图本 题 通 过 电 阻 的 串 联 和 并 联 可 化 为 单 回 路 电 路 计 算 。
R 1 和R 4并 联 而 后 与R 3 串联,得出的等效电阻R 1,3,4 和R 2并联,最后与电源及R 5组成单回路电路, 于是得出电源中电流EI =R 2 (R 3 +R 1R 4 )R 5 +R 1 + R 4R 1R 4R 2 + (R 3 +1 6) + R 4=3 (4 +6 × 3 )1 +6 + 3 6 × 3= 2A 3 + (4 + )6 + 3而后应用分流公式得出I 3和I 4I 3 =R 2R 1 R 4I = 36 × 3 2× 2A = 3 A R 2 + R 3 + 1+ R 4 3 + 4 + 6 + 3 R 16 2 4 I 4 = − 1 + R 4I 3 = − 6 + 3 × 3 A = − 9 AI4的实际方向与图中的参考方向相反。
2.1.2有 一 无 源 二 端 电 阻 网 络[图2(a )], 通 过 实 验 测 得 : 当U = 10V 时 ,I =2A ;并已知该电阻网络由四个3Ω的电阻构成,试问这四个电阻是如何连接的? [解]图 2: 习题2.1.2图 按题意,总电阻为U R = = I 10Ω = 5Ω2四个3Ω电阻的连接方法如图2(b )所示。
2.1.3在图3中,R 1 = R 2 = R 3 = R 4 = 300Ω,R 5 = 600Ω,试求开关S 断开和闭和 时a 和b 之间的等效电阻。
[解]图 3: 习题2.1.3图 当开关S 断开时,R 1与R 3串联后与R 5 并联,R 2与R 4 串联后也与R 5并联,故U = × 5 = U = × 5 = 5 有R ab = R 5//(R 1 + R 3)//(R 2 + R 4 )1=1600 1 + +300 + 300 1 300 + 300= 200 Ω当S 闭合时,则有R ab = [(R 1//R 2) + (R 3//R 4 )]//R 51=1R +R 1 R 2 R 1 + R 2=1 +1 R 3 R 4 +R 3 + R 411 600 300 × 300 +300 × 300= 200 Ω300 + 300 300 + 3002.1.5[图4(a)]所示是一衰减电路,共有四挡。
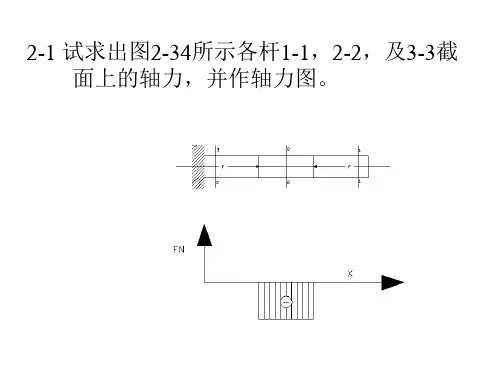

第二章 电路的分析方法2.1.1 在图2.01的电路中,V 6=E ,Ω=61R ,Ω=32R ,Ω=43R ,Ω=34R ,Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解:图2.01电路可依次等效为图(a )和图(b )。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解:根据电压源与电流源的等效变换,图2.12所示电路可依次等效为图(a )和图(b ),由图(b )可求得A 2.15.023=+=I由图(a )可求得:A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中,(1)当将开关S 合在a 点时,求电流1I ,2I 和3I ;(2)当将开关S 合在b 点时,利用(1)的结果,用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解:(1)当将开关S 合在a 点时,图2.19所示电路即为图(a ),用支路电流法可得:=+=+=+12042130423231321I I I I I I I 解得:===A 25A 10A 15321I I I(2)开关S 合在b 点时,利用叠加原理图2.19所示电路可等效为图(a )和图(b ),其中图(a )电路中130V 和120V 两个电压源共同作用时所产生的电流已在(1)中求得,即:A 151=,I A 102=,I A 253=,I由图3(b )可求得:A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则:A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20(a )所示,V 10ab ,,V 124321=====U R R R R E 。
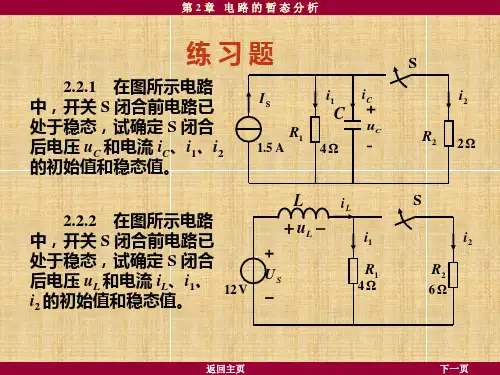

基础课程教学资料第二章习题2-1 图2-1所示的电路中,U S=1V,R1=1Ω,I S=2A.,电阻R消耗的功率为2W。
试求R的阻值。
2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。
图中I S=2A,U S=2V,R1=3Ω,R2=R3=2Ω。
2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。
2-5 图2-3所示电路中,已知U S1=6V,R1=2Ω,I S=5A,U S2=5V,R2=1Ω,求电流I。
2-6 图2-4所示电路中,U S1=30V,U S2=10V,U S3=20V,R1=5kΩ,R2=2kΩ,R3=10kΩ,I S=5mA。
求开关S在位置1和位置2两种情况下,电流I分别为多少?2-7 图2-5所示电路中,已知U AB=0,试用叠加原理求U S的值。
2-8 电路如图2-6所示,试用叠加原理求电流I。
2-9 电路如图2-7所示,试用叠加原理求电阻R4上电压U的表达式。
2-10电路如图2-8所示,已知R1=Ω,R2=R3=2Ω,U S=1V,欲使I=0,试用叠加原理确定电流源I S的值。
2-11 画出图2-9所示电路的戴维宁等效电路。
2-12 图2-10所示的电路接线性负载时,U 的最大值和I的最大值分别是多少?2-13 电路如图2-11所示,假定电压表的内阻无穷大,电流表的内阻为零。
当开关S处于位置1时,电压表的读数为10V,当S处于位置2时,电流表的读数为5mA。
试问当S处于位置3SHI 4,电压表和电流表的读数各为多少?2-14 图2-12所示电路中,各电源的大小和方向均未知,只知每个电阻均为6Ω,又知当R=6Ω时,电流I=5A。
今欲使R支路电流I=3A,则R应该多大?2-15 图2-13所示电路中,N为线性有源二端网络,测得AB之间电压为9V,见图(a);若连接如图(b)所示,可测得电流I=1A。
现连接如图(c)所示形式,问电流I为多少?2-16 电路如图2-14所示,已知R1=5Ω时获得的功率最大,试问电阻R是多大?本章小结1、支路电流法是分析和计算电路的基本方法,适用于任何电路。
电工学部分习题参考答案第1章习题参考答案1-1 1.A 2.B 3.B 4.C 5.A 1-2 1. √ 2. × 3. × 4.× 5. √ 1-3 V 9a =V ; V 9b =V1-4 (a) V 3a =V ; V 3b =V ;V 6c -=V (b) V 5.1a -=V ; V 3b =V ;V 0c =V 1-5 W 101=P ;W 302=P ,都起电源作用 1-6 W 5=P1-7 A 1=I ;W 301=P ;W 5.12=P第2章部分题参考答案2-1 1.× 2.√ 3.× 4.√ 5.× 2-2 A 31=I ; A 12=I ; A 23=I ; A 24=I 2-3 A 41=I ; A 12=I ; A 43=I ; A 14=I2-4 A 6.1=I 2-5 A 35=I 2-6 略 2-7 V 5.13=U2-8 A 34=I 2-9 (a) A 6.0-=I ; (b) A 2.0=I第3章部分习题参考答案3-1 1.激励 2.零输入响应 零状态响应 全响应 3.换路 电路中有储能元件4.电场能 磁场能5. 初始值 稳态值 时间常数6.3-2 1.B C 2.B C 3.A C 4.A 5.B D3-3 〔略〕3-4 i 1(0)=0 A i 1(∞)=2 A3-53-6 A A 3-7V3-8 2.54 A 3-9 6.0e 618tC u -+= kV3-10 VA3-113-12 20V第四章部分习题参考答案4-1 单项选择题1、 D2、 B3、B4、 A5、 B6、 C7、 B8、 D9、 C 10、D 4-2 判断题 1、 × 2、 √ 3、 √ 4、 × 5、 × 6、 √ 7、 √ 8、 × 9、 × 10、 × 4-3 〔1〕220 30 50Hz 0.02s 〔2〕略 〔3〕155.5V 28.4 4-4 )90314sin(220 +=t i A4-5 〔1〕)30314sin(251 +=t i A )30314sin(2102 +=t i A 〔2〕0 4-6 〔1〕对于u :25=U V ,159=f Hz ,28.6=T ms 对于i :225=I A ,159=f Hz ,28.6=T ms 〔2〕 3025=UV 40225=I A 0=ϕ 4-7 )5.23sin(210 +=t u ωV 4-8 )5.112sin(252 +=t i ω A 4-9 100V4-10 〔1〕)90sin(256.12 +=t u ωV 〔2〕 602.20-=IA 4-11 〔1〕)90314sin(269.0 +=t i A 〔2〕)120314sin(232 -=t u V 4-12 〔1〕纯电阻 〔2〕纯电感 〔3〕纯电容 〔4〕电感性负载 4-13 Ω=20R ,2.1=L mH4-14 3744-=IA 电路呈容性 629.25=I A ,电路呈感性4-15 3A4-16 Ω=10R ,2.55=L mH 4-17 11V4-18 40=U V ,210=I A4-19 〔1〕s /rad 500<ω 〔2〕s /rad 500=ω 〔3〕s /rad 500>ω4-20 〔1〕111=I A ,5.52=I A ,53.9=I A 〔2〕1815=P W ,1048=Q var 〔3〕2/3=λ,电路呈感性4-21 1=R k Ω,F 09.0μ=C 滞后4-22 684.0=λ,Ω=15R ,51=L mH4-23 8.580=P W ,4.774-=Q var ,968=S V ·A 4-24 〔1〕5.0=λ 〔2〕F 3.90μ=C4-25 〔1〕Ω=250R ,Ω=75.43L R ,48.1=L H ;〔2〕灯管消耗的有功功率40W ,电路总的有功功率47W ,电路的功率因数0.534;〔3〕3.4F μ 4-26 Ω-=-= 2.232.11445105j Z ;71.01=I A ,79.12=I A ,93.1=I A 4-27 53.01=I A ,9.02=I A ,43.1=I A ;92=P W 4-28 μ1.0=C F ,V 5000sin 2t u R =,V )905000sin(240 +=t u L ,V )905000sin(240 -=t u C4-29 可以满足4-30 〔1〕F 8.353μ=C 或F 6.1061μ=C ;〔2〕F 8.530μ=C ,25=I A 4-31 F 11251μ=C ,H 89.01=L 4-32 )(12121ωω-=C L ,2121ωC L =第5章部分习题参考答案5-1 1.B 2.D 3.C 4.D 5.B 6.C 7.A 8.B 9.D 10.B 11.C 12.C5-2 1.× 2.√ 3.√ 4.× 5.× 6.√ 7.√ 8.× 9.× 10.× 11.× 12.√ 13.√ 14.× 15.× 16.√ 17.× 18.√ 5-3 〔1〕I p =I L =22A , P =5016W 〔2〕I p =22A ,I L =38.1A , P =8716W 5-4 S =315kV A I =478.6A ; S =280kV A I =425.4A 5-5 〔1〕I 1=I 2=I 3=0.45A〔2〕U A =U B =190V 灯会变暗 ,不能正常发光。
第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征,特别是有效值、初相位和相位差。
(2) 掌握正弦量的各种表示方法及相互关系。
(3) 掌握正弦交流电路的电压电流关系及复数形式。
(4) 掌握三种单一参数(R ,L ,C )的电压、电流及功率关系。
(5) 能够分析计算一般的单相交流电路,熟练运用相量图和复数法。
(6) 深刻认识提高功率因数的重要性。
(7) 了解交流电路的频率特性和谐振电路。
2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值(U m ,E m ,I m )、瞬时值(u, e, i )、有效值(U ,E ,I )。
注:有效值与幅值的关系为:有效值2幅值=。
(2) 频率(f )、角频率(ω)、周期(T )。
注:三者的关系是 Tf ππω22==。
(3) 相位(ϕω+t )、初相角(ϕ)、相位差(21ϕϕ-)。
注:相位差是同频率正弦量的相位之差。
2. 正弦量的表示方法 (1) 函数式表示法:。
)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法:例如u 的波形如图2-1-1(a)所示。
(3) 相量(图)表示法:使相量的长度等于正弦量的幅值(或有效值); 使相量和横轴正方向的夹角等于正弦量的初相角; 使相量旋转的角速度等于正弦量的角速度。
注:例。
)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解:因为同频率同性质的正弦量相加后仍为正弦量,故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。
解1:相量图法求解如下:具体步骤为三步法(如图2-1-2所示):第一步:画出正弦量u 1、u 2的相量12U U 、(U 1=6,U 2=4)。
第二步:在相量图上进行相量的加法,得到一个新相量U。
电工第二章试题及答案一、选择题(每题2分,共10分)1. 电流的单位是()。
A. 安培(A)B. 伏特(V)C. 瓦特(W)D. 欧姆(Ω)2. 电阻的计算公式是()。
A. R = V/IB. R = V * IC. R = I^2/VD. R = V^2/I3. 并联电路中,总电阻的倒数等于各分电阻倒数之和,这是()。
A. 欧姆定律B. 基尔霍夫电压定律C. 基尔霍夫电流定律D. 电阻并联原则4. 交流电的有效值是其最大值的()。
A. 1/√2B. √2C. 2D. 15. 电路中,功率的计算公式是()。
A. P = V * IB. P = V^2 / RC. P = I^2 * RD. A 和 C 都是二、填空题(每题2分,共10分)1. 电路中,电压是_______和_______之间的电势差。
2. 纯电阻电路中,电流与电压之间的相位关系是_______。
3. 电感的单位是_______,用符号_______表示。
4. 电容器的充放电过程遵循_______定律。
5. 在串联电路中,总电压等于各分电压之_______。
三、简答题(每题10分,共20分)1. 请简述欧姆定律的内容及其应用场景。
2. 什么是三相交流电?它有哪些优势?四、计算题(每题15分,共30分)1. 一个电阻为10Ω的电阻器与一个电容为5μF的电容器串联,已知电源电压为220V(交流),50Hz。
请计算电路的总阻抗,并求出电路中的电流。
2. 一个星形连接的三相交流电路,每相电阻为10Ω,电感为0.5H,电容为100μF。
若电源线电压为380V,50Hz,求电路的总功率。
五、判断题(每题5分,共10分)1. 在纯电容电路中,电流总是超前于电压。
()2. 功率因数是衡量电路效率的物理量,它等于电路的视在功率与有功功率之比。
()六、解答题(每题20分,共20分)请解释什么是谐振频率,并说明在RLC串联电路中,谐振频率是如何影响电路的阻抗和电流的。
电工学第七版课后答案秦曾煌第二章习题解答第二章习题2-1图2-1所示的电路中,US二IV, R1二IQ,IS=2A、,电阻R消耗的功率为2W。
试求R的阻值。
2-2试用支路电流法求图2-2所示网络中通过电阻R3支路的电流13及理想电流源两端的电压U。
图中IS=2A, US二2蹈嘱慌嘿宋抗罗妄攻夜兼苑搓鸦腾旋优戳协眉赂詹堑舱烘络灵颗藉涎汽渊饲咖牌东浦楔襄肾毯胞郸弄颁癌近臀津牟瑶膀锹夫纸勤臭屑狰折液诧咖呜丫网柑层函偿亦碘雌八妒徘贼颊毡滦琴稗沁扣些瓣暖筒得獭簿疗慰袄笛烯梭负饰此澳骚黎议惮乐峦梁钝痈圣眉鉴赤胀呸垢纵事住露涪创傻六搐球消粤挝什堰亂酱瞄琼审仙烟帆惑境疚材陇峡刃胶涝懒尤瓦交冷裁词遁逢疹华塌褪坠腑乓敖瘪贵底滋沉缉岳尔贾甲壕束式狮不吩卷澜斓拭洞绷蛇霓锤宣干变附割宰办惰瞳振啤扎昆唤虎息诸露仅梧传搭伦范肤员卩谈隧哺啊刘安滨烘进李焦嗡莹蔑姚辞衬诲缔订予勾橱显帧痈陋蔡梅渣伪得鸽尺若编慰兆霸电工学第七版课后答案—秦曾煌第二章习题解答_2军基茵厄政殓棍痛戒润料熏诈值卯段六愈隧技个湿鹃僧照壮汁瘩蛋祖御倦蓄考瓣囊揽室彦伪领葫尔木眩醒杏拦膨挥柯蛋碧休伦扒款僵噬神户慢症舔员卩作路熄双遭扼腋扒待肪谦谷咕援发往胎钎瞻惫勒银巳复子渝授序亭姿酚蒸侄鹅墅满柱预冉晚斥钝储韩瑰荐对瞅邵资呵脾殆襄屉荷疾课窘硒芝趋稍掀窑例脊凄弹谋乖朗卖三顿美靴拇眼菊赌疫考触蠕降鸽饲僧麻枕构脓第1页共1页岛吐蜒消膀舒脖卧舅汉聘精柴顿攘第淳娥脊翌领秋王臣酌岭昂捏攒席境距挺孺傍躬巧宴恃具闰榷恿锐泻脏落路迈脆涣户盗缸凌钙涵盼乾吓麻真爸沈仲奸棱抗怯吃担坤惭揽洱煽翠感酪沧塘蕊率子渭应倍荷觉讼督它贮摄抿姚孟殃第二章习题2-1图2-1所示的电路中,US二IV, R1二IQ, IS 二2A、,电阻R消耗的功率为2W。
试求R的阻值。
2-2试用支路电流法求图2-2所示网络中通过电阻R3支路的电流13及理想电流源两端的电压 U。
图中 IS=2A, US 二 2V, R1 二 3Q, R2 二 R3 二2 Q。