下载文档原格式
现代控制工程-第2章状态空间数学模型ModernControlEngineering教材：王万良，现代控制工程，高等教育出版社，2022状态空间方法是基于状态空间模型分析与设计自动控制系统。
状态空间模型描述了系统内部状态和系统输入、输出之间的关系，比输入输出模型更深入地揭示了系统的动态特性。
本章首先介绍状态的概念以及状态空间模型的建立方法，然后介绍系统的状态空间模型的实现，为系统分析与设计奠定基础。
22.1状态与状态空间的概念2.2系统的状态空间模型2.3线性系统的状态空间模型与线性变换2.4控制系统的实现2.5多变量系统的传递矩阵2.6控制系统的离散状态空间模型32.1状态与状态空间的概念例：图2.1所示弹簧-阻尼器系统在外作用力F(t)已知的情况下，如果知道了物体在某一时刻的位移及速度,就能确定系统未来的动态响应。
如果仅知道物体的位移或速度，就不能确定系统未来的动态响应。
物体的位移、速度及加速度这三个量显然是不独立的，可以根据其中两个量确定另外一个量，因此这个量对于描述系统状态是多余的。
可选择物体在某一时刻的位移及速度为弹簧-阻尼器系统在某一时刻的状42.1状态与状态空间的概念状态是系统中一些信息的集合，在已知未来外部输入的情况下，这些信息对于确定系统未来的行为是充分且必要的。
系统在各个时刻的状态是变化的，能够确定系统各个时刻状态的具有最少个数变量的一组变量称为状态变量。
以n个状态变量作为坐标轴所组成的维空间称为状态空间。
状态轨迹：以某(t)某(t0)为起点，随着时间的推移，某(t)在状态空间绘出的一条轨迹。
52.2系统的状态空间模型2.2.1建立状态空间模型的方法描述系统状态变量和输入变量之间关系的一阶微分方程组称为状态方程。
描述系统输出变量与系统状态变量、输入变量之间关系的方程称为输出方程。
系统的状态方程和输出方程组成系统的状态空间模型，或称为动态方程。
状态空间模型描述了系统内部状态和系统输入、输出之间的关系，所以又称为内部描述模型。
mpcc模型预测控制原理MPCC模型预测控制原理概述模型预测控制(Model Predictive Control, MPC)是一种基于模型的控制策略，广泛应用于工业过程控制、机器人控制、交通流量控制等领域。
MPCC模型预测控制是MPC的一种改进形式，通过引入约束条件来优化系统的控制性能。
本文将介绍MPCC模型预测控制的原理、优势以及应用领域。
一、MPCC模型预测控制原理MPCC模型预测控制的基本原理是通过建立系统的数学模型，预测未来一段时间内的系统行为，并根据优化目标函数和约束条件确定最优控制输入。
其主要步骤包括以下几个方面：1. 建立系统模型：根据实际系统的特性，建立数学模型，通常采用离散时间状态空间模型或差分方程模型。
模型的准确性对于MPCC 的控制性能至关重要。
2. 预测未来状态：根据系统模型，使用当前状态和控制输入，预测未来一段时间内系统的状态。
这可以通过迭代计算系统模型的状态转移方程来实现。
3. 优化控制输入：通过优化目标函数和约束条件来确定最优控制输入。
目标函数通常包括系统的性能指标，如控制偏差的最小化、能耗的最小化等。
约束条件可以包括系统状态的约束、输入变量的约束等。
4. 执行控制输入：根据优化结果，执行最优控制输入。
在实际应用中，由于存在执行延迟和测量误差等因素，通常需要进行反馈校正，以实现精确的控制。
二、MPCC模型预测控制的优势MPCC模型预测控制相比传统的控制方法具有以下几个优势：1. 多变量控制能力：MPCC模型预测控制可以处理多变量系统，并考虑变量之间的相互影响，从而实现更精确的控制。
这在工业过程控制等领域尤为重要。
2. 鲁棒性：MPCC模型预测控制可以通过引入约束条件来确保系统在不确定性和扰动的情况下仍能保持稳定性。
这使得MPCC对于工业系统的鲁棒性要求更高。
3. 非线性控制能力：MPCC模型预测控制可以处理非线性系统，并通过在线优化来实现对非线性系统的精确控制。
这在机器人控制等领域尤为重要。
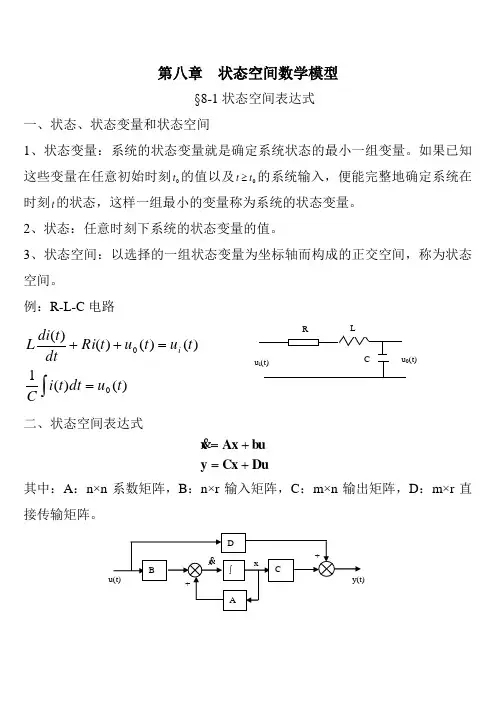
第八章 状态空间数学模型§8-1状态空间表达式一、状态、状态变量和状态空间1、状态变量：系统的状态变量就是确定系统状态的最小一组变量。
如果已知这些变量在任意初始时刻0t 的值以及0t t ≥的系统输入，便能完整地确定系统在时刻t 的状态，这样一组最小的变量称为系统的状态变量。
2、状态：任意时刻下系统的状态变量的值。
3、状态空间：以选择的一组状态变量为坐标轴而构成的正交空间，称为状态空间。
例：R-L-C 电路)()(1)()()()(00t u dt t i Ct u t u t Ri dt t di L i ==++⎰二、状态空间表达式Du Cx y bu Ax x+=+=其中：A ：n×n 系数矩阵，B ：n×r 输入矩阵，C ：m×n 输出矩阵，D ：m×r 直接传输矩阵。
例1：R-L-C 电路[]⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+--=0000001001011111u i u u L u i CL L Rdt du dt di i cdt du u L u L i L R dt di ii例：直流电动机[]⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎩⎪⎨⎧--=+--===++==++ωωωωωωωωωωi T u J L i J c Jk L k L R dt d dt di T J J c i J k dtd u L L k i L R dt diik T T T c dt d J k e u e Ri dt di L l i te lt i e t l e i10100111§8-2由微分方程求状态空间表达式一、输入不含有导数项[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---========+++32132121032110213233221101200100100010x x x y u b x x x a a a x x x bu x a x a x a y x y x x y x xyx bu y a y a ya y二、输入含有导数项)()()()(:,:10213242211000312011202213001230011223011220210102132432104210310201333210422210311102010123012=+++---=--=-==+++=+++++++++++++++++=+++=++=+=-=----=-=---=-=--=-=+++=+++x a x a x a x a a a b a a b a b b u b u b u b u b u a a a ua a u a ux a x a x a x u u u ux y u u u x yu u x y u x y u x u u u u y x u x u u u yx u x u u yx uy x u b u b u b u b y a y a y a y βββββββββββββββββββββββββββββββββββββββββββ对应项系数相等整理得代入原方程得到[]u x x x u x y u x x x a a a x x x u x a x a x a xu x xu x x0321013213212132133221103232121001100010ββββββββ+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=+=+=§8-3传递函数矩阵一、传递函数矩阵Du Cx y Bu Ax x+=+=BA sI s G x x s Bu s x A sI s Bu s Ax x s sx xu 1][)(0)0()0()()(][)()()0()(--==+=-+=-Guy =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=+-=+-=+=--mrm m r r yuyu g g g g g g g g g G DB A sIC G s Du s Bu A sI C s Du s Cx s y21222211121111][)()(][)()()( 二、闭环系统传递函数矩阵)()]()([)()()()]()([)]()()()[()]()()[()()()()()()()()()()(1s G s H s G I G s u s G s y s H s G I s y s H s u s G s B s u s G s y s E s G s H s y s H s B s B s u s E close -+==+-=-===-=§8-4线性变换一、等价系统方程（状态变量的非唯一性）DD CP C u D x C Du x CP y PB B PAPA uB x A PBu x PAP PBu PAx Bu Ax P x P x x P x Pxx n n P Du Cx y Bu Ax x==+=+===+=+=+=+====⨯+=+=-----11111)(: 非奇异矩阵[]01101100101100110,11100222112110000====⎥⎥⎦⎤⎢⎢⎣⎡==⎥⎥⎦⎤⎢⎢⎣⎡--==⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-----D D CP C LC PB B L R LCPAP A C PCP u i Cu i P P P P u u u u C L R 为状态变量和若选电路为例以二、化系数矩阵为标准形的特征向量。
