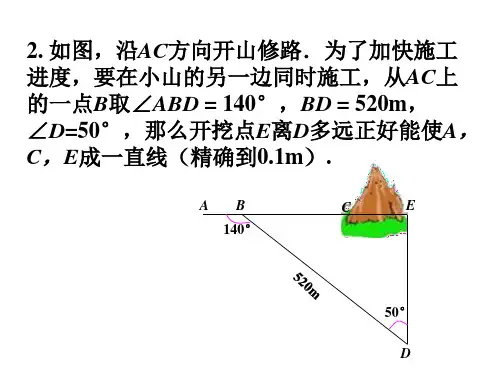
282解直角三角形

28.2解直角三角形教案篇一：28.2解直角三角形及其应用教学设计教案教学准备1.教学目标知识技能使学生理解直角三角形中五个元素的关系，会运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形。

过程方法通过综合运用勾股定理，直角三角形的两个锐角互余及锐角三角函数解直角三角形，逐步培养学生分析问题、解决问题的能力。

情感态度渗透数形结合的数学思想，培养学生良好的学习习惯。

2.教学重点/难点教学重点直角三角形的解法。

教学难点三角函数在解直角三角形中的灵活运用。

3.教学用具4.标签教学过程板书篇二：数学：28.2解直角三角形教案28.2解直角三角形【探究目标】1．目的与要求能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题．2．知识与技能能根据直角三角形中的角角关系、边边关系、边角关系解直角三角形，能运用解直角三角形的知识解决有关的实际问题．3．情感、态度与价值观通过解直角三角形的应用，培养学生学数学、用数学的意识和能力，激励学生多接触社会、了解生活并熟悉一些生产和生活中的实际事物．【探究指导】教学宫殿在直角三角形中，由已知元素求出未知元素的过程，叫做解直角三角形．解直角三角形的依据是直角三角形中各元素之间的一些相等关系，如下图：222角角关系：两锐角互余，即∠a+∠B＝90°；边边关系：勾股定理，即a?b?c；边角关系：锐角三角函数，即a,cosa?cbsinB?,cosB?csina?b,tana?ca,tanB?ca,cota?bb,cotB?abaab解直角三角形，可能出现的情况归纳起来只有下列两种情形：(1)已知两条边(一直角边和一斜边；两直角边)；(2)已知一条边和一个锐角(一直角边和一锐角；斜边和一锐角)．这两种情形的共同之处：有一条边．因此，直角三角形可解的条件是：至少已知一条边．用解直角三角形的知识解决实际问题的基本方法是：把实际问题抽象成数学问题(解直角三角形)，就是要舍去实际事物的具体内容，把事物及它们的联系转化为图形(点、线、角等)以及图形之间的大小或位置关系．借助生活常识以及课本中一些概念(如俯角、仰角、倾斜角、坡度、坡角等)的意义，也有助于把实际问题抽象为数学问题．当需要求解的三角形不是直角三角形时，应恰当地作高，化斜三角形为直角三角形再求解．在解直角三角形的过程中，常会遇到近似计算，如没有特殊要求外，边长保留四个有效数字，角度精确到1′．例1在△aBc中，∠c＝90°，根据下列条件解直角三角形．(1)c＝10，∠B＝45°，求a，b，∠a；(2)a?2,b?62，求c，∠a，∠B思路与技巧求解直角三角形的方法多种多样，如(1)可以先求a或b，也可以先求∠a，依据都是直角三角形中的各元素间的关系，但求解时为了使计算简便、准确，一般尽量选择正、余弦，尽量使用乘法，尽量选用含有已知量的关系式，尽量避免使用中间数据．解答(1)∠a＝90°-45°＝45°a?c?sina?10?sin45??52b?a?5222c?a?b?24?72?6(2)sina?24?1,2所以?a?30??B?90???a?60?例2如图，cd是Rt△aBc斜边上的高，Bc?2，cd?22,求ac，aB，∠a，∠B(精确到1′)．思路与技巧在Rt△aBc中，仅已知一条直角边Bc的长，不能直接求解．注意到Bc和cd在同一个Rt△Bcd中，因此可先解这个直角三角形．解答在Rt△Bcd中Bd?Bc2?cd2??8?2sinB?cosB?cd22??Bc233Bd2??Bc233用计算器求得∠B＝54°44′于是∠a＝90°-∠B＝35°16′在Rt△aBc中，aB?Bc3?23??6cosB6?263ac?aB?sinB?6?例3气象台测得台风中心在某港口a的正东方向400km处，正在向正西北方向转移，距台风中心300km的范围内将受其影响，问港口a 是否会受到这次台风的影响?思路与技巧如图19—48，就是要求出a到台风移动路线Bc的距离是否大于300km，Rt△aBc中，∠acB＝90°，∠aBc＝45°，aB＝400km，是ac可求．解答在Rt△aBc中，ac?sin?aBc由于aB所以ac＝aB·sin∠aBc＝400×sin45°?400?2?2?283?3002所以港口a将受到这次台风的影响．例4如图，两幢建筑物的水平距离为56．5m，从较高的建筑物的顶部看较低的建筑物的底部的俯角是42°，从较低的建筑物的顶部看较高建筑物顶部的仰角是22°，求这两幢建筑物的高度(精确到0．1m)．思路与技巧如图，aB、cd表示两幢建筑物，aB⊥Bd，cd⊥Bd，Bd＝56．5m，根据俯角、仰角的意义，∠daE＝42°，∠acF＝22°，于是Rt△aBd、Rt△acF都可解．解答在Rt△aBd中，∠adB＝∠daE＝42°Bd＝56.5(m)aB＝Bd·tan∠adB＝56.5×tan42°≈50.9(m)在Rt△acF中，aF＝cF·tan∠acF=56.5×tan22°≈22.8(m)所以cd＝aB-aF＝28.1(m)答：两幢建筑物的高度分别为50.9m，28.1m例5如图，沿水库拦水坝的背水坡，将坝顶加宽2m，坡度由原来的1：2改为1：2．5，已知坝高6m，坝长50m求：(1)加宽部分横断面aFEB的面积；(2)完成这一工程需要多少土方?思路与技巧只须求出梯形aFEB的下底EB的长，作aG⊥Bc，FH⊥EB，垂足分别为G、H，根据坡度的意义，可以求出坡aB、坡EF的水平长度．解答(1)作aG⊥Bc，FH⊥EB，垂足分别为G、H，由题意得HG＝aF ＝2(m)．aG＝FH＝6(m)在Rt△aBG中，因为i?aG1?BG2所以BG＝2×6＝12(m)在Rt△FEH中，因为i?FH1?EH2.5所以EH＝2．5×6＝15(m)所以EB＝EH+HG-BG＝15+2-12＝5(m)所以S梯形aFEB?1?aF?EB??aG?1?2?5??6?21m222??V?S梯形aFEB?50?21?50?1050m3答：加宽部分横断面aFEB的面积为21m，完成这一工程需要1050方土．例6海上有两条船，甲船在乙船的正南方向，甲船以每小时40海里的速度沿北偏东60°方向航行，乙船沿正东方向以每小时20海里的速度航行，问两船会不会相撞?为什么?思路与技巧根据题意画出图形，如图19—51，可知甲、乙两船的路线可能会成为直2??角三角形中60°所对的直角边和斜边，两船同时出发，在相同的时间内所走路程的比如果正好等于60°的正弦就会相撞，否则不会．解答如图，因为乙船的速度为每小时20海里，甲船的速度为每小时40海里，所以乙船与甲船所走路程的比为1：2．又sin60??1?22所以不会发生相撞．例7某市为改变城市交通状况，在大街拓宽工程中，要伐掉一棵树aB．在地面上事先划定以B为圆心，半径与aB等长的圆形危险区，现在某工人站在离B点3m远的d点测得树的顶部a点的仰角为60°，树的底部B的仰角为30°，如图19—52，问距离B点8m远的保护物是否在危险区内?思路与技巧本题的实质是要计算大树的高度，如果大于8m，说明保护物在危险区内，否则不在．由于大树不在哪一个直角三角形中，根据条件，过c作cE⊥aB，则可把aB放在Rt△acE和Rt△BcE中进行求解．解答过c作cE⊥aB，垂足为E.由题意可知，cE＝dB＝3m在Rt△cEB 中，。