结构的动力计算
- 格式:doc
- 大小:599.50 KB
- 文档页数:13




第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
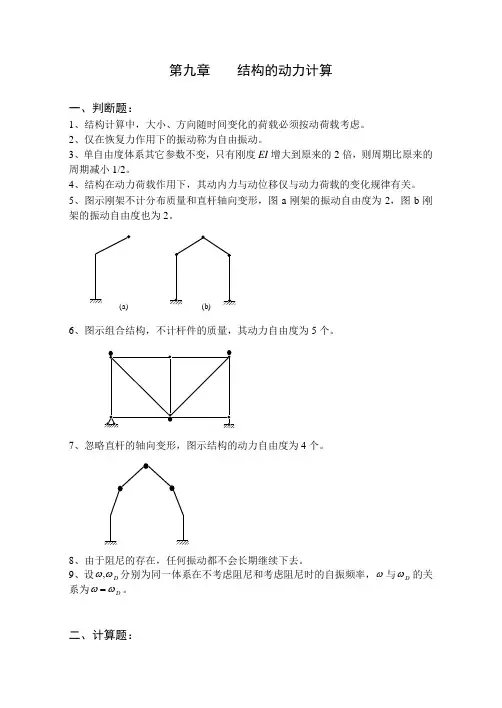
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。




混凝土结构的动力计算原理一、引言混凝土结构是现代建筑领域中最常用的结构形式之一。
在建筑设计和施工过程中,需要对混凝土结构进行动力计算,以保证其在地震、风荷载等自然灾害或人为因素的作用下具有足够的稳定性和安全性。
本文将详细介绍混凝土结构的动力计算原理。
二、混凝土结构的基本力学性质混凝土结构的力学性质包括强度、刚度和稳定性。
其中,强度是指混凝土结构在承受外力作用下不发生破坏的能力;刚度是指混凝土结构在受到外力作用后变形的程度;稳定性是指混凝土结构在受到外力作用后能够保持稳定的程度。
三、混凝土结构的动力计算方法混凝土结构的动力计算方法可以分为静力计算和动力计算两种。
静力计算是指在结构不受外力作用时,根据静力平衡原理计算结构的内力和变形情况。
动力计算是指在结构受到外力作用时,根据结构动力学原理计算结构的响应和变形情况。
四、混凝土结构的动力学原理混凝土结构的动力学原理包括自由振动、强迫振动和响应谱分析三种方法。
1. 自由振动自由振动是指在结构不受外力作用下,结构自身的固有频率下产生的振动。
自由振动的计算方法可以使用下面的公式:ωn = (k/m)1/2其中,ωn为结构的固有频率,k为结构的刚度,m为结构的质量。
2. 强迫振动强迫振动是指在结构受到外力作用下,产生的振动。
强迫振动的计算方法可以使用下面的公式:F(t) = m*a + c*v + k*x其中,F(t)为外力,m为结构的质量,a为结构的加速度,c为结构的阻尼系数,v为结构的速度,k为结构的刚度,x为结构的位移。
3. 响应谱分析响应谱分析是指根据结构的动力学特性和地震激励谱,计算结构在地震作用下的响应。
响应谱分析的计算方法可以使用下面的公式:Sd = Sa(Ta)*Cs(T)其中,Sd为结构的位移响应谱,Sa(Ta)为地震激励谱,Cs(T)为结构的加速度反应系数。
五、混凝土结构的动力计算实例以一座混凝土框架结构为例,该结构高度为50米,采用双向抗震设计,设计基本周期为0.5秒,地震烈度为7度。

结构动力计算要点研究内容:动力计算研究结构在动力荷载作用下的变形和内力,即研究结构的动力反应。
动力荷载:大小、方向、作用点随时间而变化的荷载。
结构的动力反应不但与动力荷载的性质有关,还与结构本身的动力特性直接相关。
结构本身的动力特性是结构本身固有的,如自振频率及振型。
动力计算的特点:动力计算不能忽略惯性力,这是动力计算与静力计算的本质区别。
内力和变形都是时间的函数。
动力荷载的分类:简谐性周期荷载、冲击荷载、随机荷载。
体系自由度:质点的位移就是动力计算的基本未知数。
确定运动过程中任一时刻所有质量的位置所需的独立几何参数的数目,称为该体系的自由度。
阻尼阻尼对结构的作用:一类是材料的非弹性变形,使变形能损失。
一类是阻尼力,包括介质阻力和摩擦阻力。
阻尼是振动的一个重要因素,而且很复杂,需化简;把各种阻尼综合作用假定为受一个阻尼力作用。
并且假定阻尼力的大小与质点的运动速度成正比,这一假定称为粘滞阻尼理论。
自振周期T:振动一周需要的时间;单位:“s(秒)”自振频率f:单位时间的振动次数;单位:“Hz(赫兹)”圆频率或频率w:2À时间内的振动次数,单位:“弧度/s”;自振周期的性质:自振周期仅与结构的质量和刚度有关;与外界的干扰力无关。
质量越大,周期越大;刚度越大,周期越小。
自振周期是结构动力性能的一个重要指标。
刚度系数:使质点产生单位位移需要施加的力。
柔度系数:质点在单位力作用下产生的位移。
动力放大系数1)简谐动荷载作用在质点上,内力动力系数与位移动力系数相同。
只须将干扰力幅值当作静荷载按静力方法计算出相应的位移、内力,再乘以动力系数b即可。
2) 简谐动荷载不作用在质点上,结构没有一个统一的动力系数先算出质体上的惯性力,再将惯性力及荷载幅值作用于结构上(如左图所示),然后按静力方法计算位移和内力。
最大位移和最大内力的计算振动体系的最大位移为最大动位移与静位移之和;振幅为动位移的幅值(最大动位移);最大内力为最大动内力与静内力之和。

第十章 结构动力计算基础
一、判断题:
1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:
10、图示梁自重不计,求自振频率ω。
l l /4
11、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2
l /2
12、求图示体系的自振频率ω。
l l
0.5l 0.5
13、求图示体系的自振频率ω。
EI = 常数。
l
l 0.5
14、求图示结构的自振频率ω。
l l
15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2
l /2
l /
18、图示梁自重不计,W EI ==⨯⋅
2002104kN kN m 2
,,求自振圆频率ω。
B
2m
2m
19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EI
EI
W
20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EI
EI
W
EI 2
21、求图示体系的自振频率ω。
各杆EI = 常数。
a a
a
22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b
的自振频率之比。
l /2
l
/2(a)
l /2
l /2
(b)
23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
3
m 3m
24、忽略质点m 的水平位移,求图示桁架竖向振动时的自振频率ω。
各杆EA = 常数。
m 4m
4m
25、图示体系E P W I =⨯====-2102052048004kN /cm s kN, kN, cm 214
,,θ。
求质点处最大动位移和最大动弯矩。
4m
m
2sin θP t
26、图示体系EI k =⨯⋅==2102035kN m s 2-1,,θ×1055N /m, P =×N 103。
kN W 10=。
求质点处最大动位移和最大动弯矩。
m
2m
2
27、求图示体系在初位移等于l/1000
,初速度等于零时的解答。
θωω=020.( 为自振频率),不计阻尼。
l
28、图示体系受动力荷载作用,不考虑阻尼,杆重不计,求发生共振时干扰力的频率θ。
/3
P t
sin( )
29、已知:m P ==38t, kN ,干扰力转速为150r/min ,不计杆件的质量,EI =⨯⋅6103kN m 2。
求质点的最大动力位移。
2
m
2m
30、图示体系中,电机重kN 10=W 置于刚性横梁上,电机转速n r =500/min ,水平方向干扰力为) sin(kN 2)(t t P θ⋅=,已知柱顶侧移刚度kN/m 1002.14
⨯=k ,自振
频率ω=-100s 1。
求稳态振动的振幅及最大动力弯矩图。
m
31、图示体系中,kN 10=W ,质点所在点竖向柔度917.1=δ,马达动荷载P t t ()sin()=4kN θ,马达转速
n r =600/min 。
求质点振幅与最大位移。
32、图示体系中,W =8kN ,自振频率ω=-100s 1
,电机荷载P (t ) = 5kN ·sin(
θt ),电机转速n = 550r/min 。
求梁的最大与最小弯矩图。
2m
2m
P t ()
33、求图示体系支座弯矩M A 的最大值。
荷载P t P t (),.==004sin θθω 。
/2
/2
34、求图示体系的运动方程。
l
l
m
0.50.5
35、求图示体系稳态阶段动力弯矩幅值图。
θωω=05.( 为自振频率),EI = 常数,不计阻尼。
l
l
l
36、图示体系分布质量不计,EI = 常数。
求自振频率。
a
a
37、图示简支梁EI = 常数,梁重不计,m m m m 122==,,已求出柔度系数
()δ123718=a
EI /。
求自振频率及主振型。
a
a
a
38、求图示梁的自振频率及主振型,并画主振型图。
杆件分布质量不计。
a
a
a
39、图示刚架杆自重不计,各杆EI = 常数。
求自振频率。
2m
2m
40、求图示体系的自振频率和主振型。
EI = 常数。
l l
l /3
/3
/3
41、求图示体系的自振频率及主振型。
EI = 常数。
l /2l /2l /2l /2
42、求图示体系的自振频率及相应主振型。
EI = 常数。
/2l l
/2l /2l /2
l
43、求图示结构的自振频率和主振型。
不计自重。
l /2l /2
44、求图示体系的自振频率和主振型。
不计自重,EI = 常数。
m a
a
a
45、求图示体系的第一自振频率。
l /2
l /2
l /2
l /2
46、求图示体系的自振频率。
已知:m m m 12== 。
EI = 常数。
m
1.51m
1.5m
1m
1m
47、求图示体系的自振频率和主振型,并作出主振型图。
已知:m m m 12==,EI = 常数。
2m
2
4m 4m
48、求图示对称体系的自振频率。
EI = 常数。
l l l l /2
/2
/2
/2
49、图示对称刚架质量集中于刚性横粱上,已知:m 1=m ,m 2=2m 。
各横梁的层间侧移刚度均为k 。
求自振频率及主振型。
m 1
m 2
2
1
50、求图示体系的自振频率并画出主振型图。
m
51、求图示体系的自振频率和主振型。
EI = 常数。
l l
52、用最简单方法求图示结构的自振频率和主振型。
l l
53、求图示体系的频率方程。
l
54、求图示体系的自振频率和主振型。
EI =常数。
2a
a
a
55、求图示体系的自振频率和主振型。
不计自重,EI = 常数。
a /2
a /2
a /2
a /2
56、求图示体系的自振频率。
设 EI = 常数。
l
57、图示体系,设质量分别集中于各层横梁上,数值均为m 。
求第一与第二自振频率之比ωω12:。
l
l
2
58、求图示体系的自振频率和主振型。
l
m m 2EI =∞ EI =∞ EI 1
EI 1
2EI 1
2EI 1
59、求图示体系的自振频率和主振型。
m m m m 122==,。
60、求图示桁架的自振频率。
杆件自重不计。
m 3m
3m
61、求图示桁架的自振频率。
不计杆件自重,EA = 常数。
m m
m
33
62、作出图示体系的动力弯矩图,已知:θ=082567
3
.EI
ml 。
0.5
l
l
2
m
63、作图示体系的动力弯矩图。
柱高均为h ,柱刚度EI =常数。
l l
θ=13257
.EI
mh
30.50.5P
64、绘出图示体系的最大动力弯矩图。
已知:动荷载幅值P =10kN ,θ=-209441
.s ,
质量m =500kg ,a =2m ,EI =⨯⋅481062
.N m 。
()
P t sin θ
65、已知图示体系的第一振型如下,求体系的第一频率。
EI = 常数。
振型101618054011 ..
⎧⎨⎪
⎩⎪⎫⎬
⎪
⎭
⎪
/2。