(3-4)
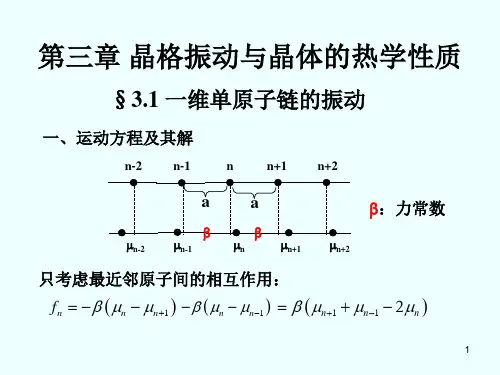
即第n个原子的加速度不仅与Un有关,且与 Un-1,Un+1有关,这意味着原子运动之间的耦合, 由于对每一个原子都有一个类似的方程,n共可 取N个值,故该式实为N个方程组成的方程组, 可有N个解,而此时晶体的总自由度也为N。
五.解方程
设λ>>a, 相邻原子的相位差小―― 可把晶体看作 是连续媒质. na x a Δx U(x,t) U(x+Δx,t) Δx 为小量 Un(t)=U(na,t)
∴ qNa = 2πm(m=0,±1,±2...) 得(3-10)式
2 q m Na
(3-10)
结论:
1. 格波的波矢q不连续; 2. q点的分布均匀, 相邻q点的间 距为 2π /(Νa); 3. λ=2π/q =Na/ m
七、讨论
(Hale Waihona Puke )格波由(3-8)表示的是一个格波,它是 简谐 行波,又称为简正格波,简正模式。格波 相速度vp(等相位面移动的速度) 设t1时刻,n1a处振动,某一确定的相 位面到t2 时刻传到n2a处,则
ω(q)= ω(q+Kh)
其中Kh为倒格矢。
倒格子平移对称性
(3-16)
由式(3-11)还可知: ω(q)= ω(-q)-―倒格子反演对称性 关于色散关系的倒格子平移对称性和反 演对称性的这两个结论对三维晶格也是 适用的。 说明:
1. q和-q对应相同的ω,但q和-q代表 了不同的格 波,与唯一性不 矛盾。 2. q的不唯一性是由晶体的不连续性所致。
把式(3-8)代入式(3-4)并用尤拉公 式整理得到 (3-11)式 2 4 2 2 qa (1 cos qa) sin m m 2
4 m