数学建模bp神经网络讲解学习
- 格式:doc
- 大小:304.50 KB
- 文档页数:13


BP神经网络概述BP神经网络由输入层、隐藏层和输出层组成。
输入层接收外界输入的数据,隐藏层对输入层的信息进行处理和转化,输出层输出最终的结果。
网络的每一个节点称为神经元,神经元之间的连接具有不同的权值,通过权值的调整和激活函数的作用,网络可以学习到输入和输出之间的关系。
BP神经网络的学习过程主要包括前向传播和反向传播两个阶段。
前向传播时,输入数据通过输入层向前传递到隐藏层和输出层,计算出网络的输出结果;然后通过与实际结果比较,计算误差函数。
反向传播时,根据误差函数,从输出层开始逆向调整权值和偏置,通过梯度下降算法更新权值,使得误差最小化,从而实现网络的学习和调整。
BP神经网络通过多次迭代学习,不断调整权值和偏置,逐渐提高网络的性能。
学习率是调整权值和偏置的重要参数,过大或过小的学习率都会导致学习过程不稳定。
此外,网络的结构、激活函数的选择、错误函数的定义等也会影响网络的学习效果。
BP神经网络在各个领域都有广泛的应用。
在模式识别中,BP神经网络可以从大量的样本中学习特征,实现目标检测、人脸识别、手写识别等任务。
在数据挖掘中,BP神经网络可以通过对历史数据的学习,预测未来的趋势和模式,用于市场预测、股票分析等。
在预测分析中,BP神经网络可以根据历史数据,预测未来的房价、气温、销售额等。
综上所述,BP神经网络是一种强大的人工神经网络模型,具有非线性逼近能力和学习能力,广泛应用于模式识别、数据挖掘、预测分析等领域。
尽管有一些缺点,但随着技术的发展,BP神经网络仍然是一种非常有潜力和应用价值的模型。

BP神经网络学习及算法1.前向传播:在BP神经网络中,前向传播用于将输入数据从输入层传递到输出层,其中包括两个主要步骤:输入层到隐藏层的传播和隐藏层到输出层的传播。
(1)输入层到隐藏层的传播:首先,输入数据通过输入层的神经元进行传递。
每个输入层神经元都与隐藏层神经元连接,并且每个连接都有一个对应的权值。
输入数据乘以对应的权值,并通过激活函数进行处理,得到隐藏层神经元的输出。
(2)隐藏层到输出层的传播:隐藏层的输出被传递到输出层的神经元。
同样,每个隐藏层神经元与输出层神经元连接,并有对应的权值。
隐藏层输出乘以对应的权值,并通过激活函数处理,得到输出层神经元的输出。
2.反向传播:在前向传播后,可以计算出网络的输出值。
接下来,需要计算输出和期望输出之间的误差,并将误差通过反向传播的方式传递回隐藏层和输入层,以更新权值。
(1)计算误差:使用误差函数(通常为均方差函数)计算网络输出与期望输出之间的误差。
误差函数的具体形式根据问题的特点而定。
(2)反向传播误差:从输出层开始,将误差通过反向传播的方式传递回隐藏层和输入层。
首先,计算输出层神经元的误差,然后将误差按照权值比例分配给连接到该神经元的隐藏层神经元,并计算隐藏层神经元的误差。
依此类推,直到计算出输入层神经元的误差。
(3)更新权值:利用误差和学习率来更新网络中的权值。
通过梯度下降法,沿着误差最速下降的方向对权值和阈值进行更新。
权值的更新公式为:Δwij = ηδjxi,其中η为学习率,δj为神经元的误差,xi为连接该神经元的输入。
以上就是BP神经网络的学习算法。
在实际应用中,还需要考虑一些其他的优化方法和技巧,比如动量法、自适应学习率和正则化等,以提高网络的性能和稳定性。
此外,BP神经网络也存在一些问题,比如容易陷入局部极小值、收敛速度慢等,这些问题需要根据实际情况进行调优和改进。

BP神经网络的基本原理_一看就懂BP神经网络(Back Propagation Neural Network)是一种常用的人工神经网络模型,用于解决分类、回归和模式识别问题。
它的基本原理是通过反向传播算法来训练和调整网络中的权重和偏置,以使网络能够逐渐逼近目标输出。
1.前向传播:在训练之前,需要对网络进行初始化,包括随机初始化权重和偏置。
输入数据通过输入层传递到隐藏层,在隐藏层中进行线性加权和非线性激活运算,然后传递给输出层。
线性加权运算指的是将输入数据与对应的权重相乘,然后将结果进行求和。
非线性激活指的是对线性加权和的结果应用一个激活函数,常见的激活函数有sigmoid函数、ReLU函数等。
激活函数的作用是将线性运算的结果映射到一个非线性的范围内,增加模型的非线性表达能力。
2.计算损失:将网络输出的结果与真实值进行比较,计算损失函数。
常用的损失函数有均方误差(Mean Squared Error)和交叉熵(Cross Entropy)等,用于衡量模型的输出与真实值之间的差异程度。
3.反向传播:通过反向传播算法,将损失函数的梯度从输出层传播回隐藏层和输入层,以便调整网络的权重和偏置。
反向传播算法的核心思想是使用链式法则。
首先计算输出层的梯度,即损失函数对输出层输出的导数。
然后将该梯度传递回隐藏层,更新隐藏层的权重和偏置。
接着继续向输入层传播,直到更新输入层的权重和偏置。
在传播过程中,需要选择一个优化算法来更新网络参数,常用的优化算法有梯度下降(Gradient Descent)和随机梯度下降(Stochastic Gradient Descent)等。
4.权重和偏置更新:根据反向传播计算得到的梯度,使用优化算法更新网络中的权重和偏置,逐步减小损失函数的值。
权重的更新通常按照以下公式进行:新权重=旧权重-学习率×梯度其中,学习率是一个超参数,控制更新的步长大小。
梯度是损失函数对权重的导数,表示了损失函数关于权重的变化率。

BP神经网络框架BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。
它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。
1BP神经网络基本原理BP神经网络的基本原理可以分为如下几个步骤:(1)输入信号Xi→中间节点(隐层点)→输出节点→输出信号Yk;(2)网络训练的每个样本包括输入向量X和期望输出量t,网络输出值Y 和期望输出值t之间的偏差。
(3)通过调整输入节点与隐层节点的联接强度取值Wij和隐层节点与输出节点之间的联接强度取值Tjk,以及阈值,使误差沿梯度方向下降。
(4)经过反复学习训练,确定与最小误差相对应的网络参数(权值和阈值),训练到此停止。
(5)经过上述训练的神经网络即能对类似样本的输入信息,自行处理输出误差最小的经过非线性转换的信息。
2BP神经网络涉及的主要模型和函数BP神经网络模型包括输入输出模型、作用函数模型、误差计算模型和自学习模型。
输出模型又分为:隐节点输出模型和输出节点输出模型。
下面将逐个介绍。
(1)作用函数模型作用函数模型,又称刺激函数,反映下层输入对上层节点刺激脉冲强度的函数。
一般取(0,1)内的连续取值函数Sigmoid函数:f x=11+e^(−x)(2)误差计算模型误差计算模型反映神经网络期望输出与计算输出之间误差大小的函数:Ep=12(tpi−Opi)2其中,tpi为i节点的期望输出值;Opi为i节点的计算输出值。
(3)自学习模型自学习模型是连接下层节点和上层节点之间的权重矩阵Wij的设定和修正过程。

BP神经⽹络2013参考数学建模常⽤⽅法:数学建模常⽤⽅法系列资料由圣才⼤学⽣数学建模竞赛⽹整理收集。
希望能对您有所帮助!BP神经⽹络⽅法摘要⼈⼯神经⽹络是⼀种新的数学建模⽅式,它具有通过学习逼近任意⾮线性映射的能⼒。
本⽂提出了⼀种基于动态BP神经⽹络的预测⽅法,阐述了其基本原理,并以典型实例验证。
关键字神经⽹络,BP模型,预测1 引⾔在系统建模、辨识和预测中,对于线性系统,在频域,传递函数矩阵可以很好地表达系统的⿊箱式输⼊输出模型;在时域,Box-Jenkins⽅法、回归分析⽅法、ARMA模型等,通过各种参数估计⽅法也可以给出描述。
对于⾮线性时间序列预测系统,双线性模型、门限⾃回归模型、ARCH模型都需要在对数据的内在规律知道不多的情况下对序列间关系进⾏假定。
可以说传统的⾮线性系统预测,在理论研究和实际应⽤⽅⾯,都存在极⼤的困难。
相⽐之下,神经⽹络可以在不了解输⼊或输出变量间关系的前提下完成⾮线性建模[4,6]。
神经元、神经⽹络都有⾮线性、⾮局域性、⾮定常性、⾮凸性和混沌等特性,与各种预测⽅法有机结合具有很好的发展前景,也给预测系统带来了新的⽅向与突破。
建模算法和预测系统的稳定性、动态性等研究成为当今热点问题。
⽬前在系统建模与预测中,应⽤最多的是静态的多层前向神经⽹络,这主要是因为这种⽹络具有通过学习逼近任意⾮线性映射的能⼒。
利⽤静态的多层前向神经⽹络建⽴系统的输⼊/输出模型,本质上就是基于⽹络逼近能⼒,通过学习获知系统差分⽅程中的⾮线性函数。
但在实际应⽤中,需要建模和预测的多为⾮线性动态系统,利⽤静态的多层前向神经⽹络必须事先给定模型的阶次,即预先确定系统的模型,这⼀点⾮常难做到。
近来,有关基于动态⽹络的建模和预测的研究,代表了神经⽹络建模和预测新的发展⽅向。
2BP神经⽹络模型BP⽹络是采⽤Widrow-Hoff学习算法和⾮线性可微转移函数的多层⽹络。
典型的BP 算法采⽤梯度下降法,也就是Widrow-Hoff算法。

BP神经网络算法BP神经网络算法(BackPropagation Neural Network)是一种基于梯度下降法训练的人工神经网络模型,广泛应用于分类、回归和模式识别等领域。
它通过多个神经元之间的连接和权重来模拟真实神经系统中的信息传递过程,从而实现复杂的非线性函数拟合和预测。
BP神经网络由输入层、隐含层和输出层组成,其中输入层接受外部输入的特征向量,隐含层负责进行特征的抽取和转换,输出层产生最终的预测结果。
每个神经元都与上一层的所有神经元相连,且每个连接都有一个权重,通过不断调整权重来优化神经网络的性能。
BP神经网络的训练过程主要包括前向传播和反向传播两个阶段。
在前向传播中,通过输入层将特征向量引入网络,逐层计算每个神经元的输出值,直至得到输出层的预测结果。
在反向传播中,通过计算输出层的误差,逐层地反向传播误差信号,并根据误差信号调整每个连接的权重值。
具体来说,在前向传播过程中,每个神经元的输出可以通过激活函数来计算。
常见的激活函数包括Sigmoid函数、ReLU函数等,用于引入非线性因素,增加模型的表达能力。
然后,根据权重和输入信号的乘积来计算每个神经元的加权和,并通过激活函数将其转化为输出。
在反向传播过程中,首先需要计算输出层的误差。
一般采用均方差损失函数,通过计算预测值与真实值之间的差异来衡量模型的性能。
然后,根据误差信号逐层传播,通过链式法则来计算每个神经元的局部梯度。
最后,根据梯度下降法则,更新每个连接的权重值,以减小误差并提高模型的拟合能力。
总结来说,BP神经网络算法是一种通过多层神经元之间的连接和权重来模拟信息传递的人工神经网络模型。
通过前向传播和反向传播两个阶段,通过不断调整权重来训练模型,并通过激活函数引入非线性因素。
BP 神经网络算法在分类、回归和模式识别等领域具有广泛的应用前景。


BP神经网络模型与学习算法BP(Back Propagation)神经网络模型是一种常用的人工神经网络模型,主要用于分类和回归问题。
BP网络由输入层、隐含层和输出层组成,利用反向传播算法进行学习和训练。
下面将详细介绍BP神经网络模型和学习算法。
-输入层:接受外界输入的数据,通常是特征向量。
-隐含层:对输入层特征进行非线性处理,并将处理后的结果传递给输出层。
-输出层:根据隐含层的输出结果进行分类或回归预测。
前向传播:从输入层到输出层逐层计算神经元的输出值。
对于每个神经元,输入信号经过带权和的线性变换,然后通过激活函数进行非线性变换,得到神经元的输出值,该值作为下一层神经元的输入。
-具有较强的非线性映射能力,可以用来解决复杂的分类和回归问题。
-学习能力强,能够从大量的训练样本中学习到隐藏在数据中的模式和规律。
-适用于处理多输入多输出问题,可以构建具有多个输入和输出的神经网络模型。
然而,BP神经网络模型也存在一些不足之处,包括:-容易陷入局部最优解,当网络层数较多时,很容易陷入局部极小点。
-对输入数据的数值范围敏感,需要对输入数据进行归一化处理,以避免权值的不平衡。
-训练时间较长,需要较大的训练集和较多的迭代次数才能达到较好的训练效果。
总结来说,BP神经网络模型是一种常用的人工神经网络模型,通过反向传播算法来实现网络的学习和训练。
BP神经网络模型具有较强的非线性映射能力和学习能力,适用于解决复杂的分类和回归问题。
然而,BP 神经网络模型也存在局部最优解问题和对输入数据的敏感性等不足之处。
因此,在实际应用中需要根据具体问题选择合适的算法和模型。
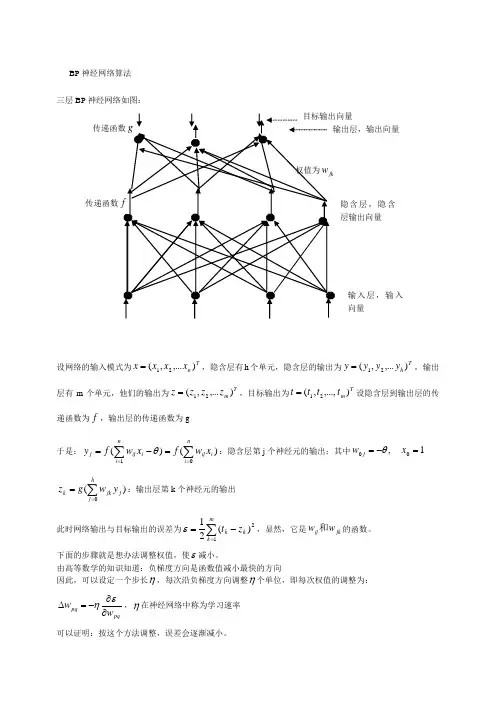
BP 神经网络算法 三层BP 神经网络如图:设网络的输入模式为Tn x x x x ),...,(21=,隐含层有h 个单元,隐含层的输出为Th y y y y ),...,(21=,输出层有m 个单元,他们的输出为Tm z z z z ),...,(21=,目标输出为Tm t t t t ),...,,(21=设隐含层到输出层的传递函数为f ,输出层的传递函数为g于是:)()(1∑∑===-=ni i ij ni iij j x w f xw f y θ:隐含层第j 个神经元的输出;其中1,00=-=x w j θ)(0∑==hj j jk k y w g z :输出层第k 个神经元的输出此时网络输出与目标输出的误差为∑=-=m k k k z t 12)(21ε,显然,它是jk ij w w 和的函数。
下面的步骤就是想办法调整权值,使ε减小。
由高等数学的知识知道:负梯度方向是函数值减小最快的方向因此,可以设定一个步长η,每次沿负梯度方向调整η个单位,即每次权值的调整为:pqpq w w ∂∂-=∆εη,η在神经网络中称为学习速率 可以证明:按这个方法调整,误差会逐渐减小。
隐含层,隐含层输出向量传递函数输入层,输入向量BP 神经网络(反向传播)的调整顺序为: 1)先调整隐含层到输出层的权值 设k v 为输出层第k 个神经元的输入∑==hj j jkk y wv 0-------复合函数偏导公式若取x e x f x g -+==11)()(,则)1()111(11)1()('2k k v v v v k z z ee e e u g kk k k -=+-+=+=---- 于是隐含层到输出层的权值调整迭代公式为: 2)从输入层到隐含层的权值调整迭代公式为: 其中j u 为隐含层第j 个神经元的输入:∑==ni i ijj x wu 0注意:隐含层第j 个神经元与输出层的各个神经元都有连接,即jy ∂∂ε涉及所有的权值ij w ,因此∑∑==--=∂∂∂∂∂-∂=∂∂m k jk k k k j k k k m k k k k j w u f z t y u u z z z t y 002)(')()(ε于是:因此从输入层到隐含层的权值调整迭代为公式为: 例:下表给出了某地区公路运力的历史统计数据,请建立相应的预测模型,并对给出的2010和2011年的数据,预测相应的公路客运量和货运量。
bp神经网络的基本原理
BP神经网络是一种常用的人工神经网络模型,用于解决分类和回归问题。
它的基本原理是通过反向传播算法来调整网络的权重和偏置,从而使网络能够学习和逼近输入输出之间的非线性关系。
BP神经网络由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据,隐藏层是网络中间的处理层,输出层给出最终的结果。
每个神经元都与前一层的神经元以及后一层的神经元相连接,每个连接都有一个权重值。
BP神经网络的学习过程首先需要给定一个训练数据集,并设置好网络的结构和参数。
然后,通过前向传播将输入数据从输入层传递到隐藏层和输出层,计算网络的输出结果。
接着,根据输出结果与实际输出之间的差异,使用误差函数来评估网络的性能。
在反向传播阶段,根据误差函数的值,利用链式法则计算每个连接的权重和偏置的梯度。
然后,根据梯度下降法更新连接的权重和偏置,使误差不断减小。
这个过程反复进行,直到网络输出的误差达到了可接受的范围或者训练次数达到了预设的最大值。
通过不断地调整权重和偏置,BP神经网络可以逐渐学习到输入输出之间的映射关系,从而在面对新的输入数据时能够给出合理的输出。
同时,BP神经网络还具有一定的容错性和鲁棒性,可以处理一些噪声和不完整的数据。
总的来说,BP神经网络的基本原理是通过反向传播算法来训练网络,将输入数据从输入层传递到输出层,并且根据实际输出与期望输出之间的差异来优化网络的权重和偏置,以达到学习和逼近输入输出之间关系的目的。
BP 神经网络原理2。
1 基本BP 算法公式推导基本BP 算法包括两个方面:信号的前向传播和误差的反向传播.即计算实际输出时按从输入到输出的方向进行,而权值和阈值的修正从输出到输入的方向进行.图2—1 BP 网络结构Fig.2-1 Structure of BP network图中:jx 表示输入层第j 个节点的输入,j =1,…,M ;ijw 表示隐含层第i 个节点到输入层第j 个节点之间的权值;iθ表示隐含层第i 个节点的阈值;()x φ表示隐含层的激励函数;ki w 表示输出层第k 个节点到隐含层第i 个节点之间的权值,i =1,…,q ;ka 表示输出层第k 个节点的阈值,k =1,…,L ; ()x ψ表示输出层的激励函数;ko 表示输出层第k 个节点的输出.(1)信号的前向传播过程 隐含层第i 个节点的输入net i :1Mi ij j ij net w x θ==+∑ (3—1)隐含层第i 个节点的输出y i :1()()Mi i ij j i j y net w x φφθ===+∑ (3-2)输出层第k 个节点的输入net k :111()qqMk ki i k ki ij j i ki i j net w y a w w x a φθ====+=++∑∑∑ (3—3)输出层第k 个节点的输出o k :111()()()qq M k k ki i k ki ij j i k i i j o net w y a w w x a ψψψφθ===⎛⎫==+=++ ⎪⎝⎭∑∑∑ (3—4)(2)误差的反向传播过程误差的反向传播,即首先由输出层开始逐层计算各层神经元的输出误差,然后根据误差梯度下降法来调节各层的权值和阈值,使修改后的网络的最终输出能接近期望值。
对于每一个样本p 的二次型误差准则函数为E p :211()2Lp k k k E T o ==-∑ (3—5)系统对P 个训练样本的总误差准则函数为:2111()2P Lp p k k p k E T o ===-∑∑ (3—6)根据误差梯度下降法依次修正输出层权值的修正量Δw ki ,输出层阈值的修正量Δa k ,隐含层权值的修正量Δw ij ,隐含层阈值的修正量i θ∆。
BP神经网络的基本原理_一看就懂BP神经网络(Back propagation neural network)是一种常用的人工神经网络模型,也是一种有监督的学习算法。
它基于错误的反向传播来调整网络权重,以逐渐减小输出误差,从而实现对模型的训练和优化。
1.初始化网络参数首先,需要设置网络的结构和连接权重。
BP神经网络通常由输入层、隐藏层和输出层组成。
每个神经元与上下层之间的节点通过连接权重相互连接。
2.传递信号3.计算误差实际输出值与期望输出值之间存在误差。
BP神经网络通过计算误差来评估模型的性能。
常用的误差计算方法是均方误差(Mean Squared Error,MSE),即将输出误差的平方求和后取平均。
4.反向传播误差通过误差反向传播算法,将误差从输出层向隐藏层传播,并根据误差调整连接权重。
具体来说,根据误差对权重的偏导数进行计算,然后通过梯度下降法来更新权重值。
5.权重更新在反向传播过程中,通过梯度下降法来更新权重值,以最小化误差。
梯度下降法的基本思想是沿着误差曲面的负梯度方向逐步调整权重值,使误差不断减小。
6.迭代训练重复上述步骤,反复迭代更新权重值,直到达到一定的停止条件,如达到预设的训练轮数、误差小于一些阈值等。
迭代训练的目的是不断优化模型,使其能够更好地拟合训练数据。
7.模型应用经过训练后的BP神经网络可以应用于新数据的预测和分类。
将新的输入数据经过前向传播,可以得到相应的输出结果。
需要注意的是,BP神经网络对于大规模、复杂的问题,容易陷入局部最优解,并且容易出现过拟合的情况。
针对这些问题,可以采用各种改进的方法,如加入正则化项、使用更复杂的网络结构等。
综上所述,BP神经网络通过前向传播和反向传播的方式,不断调整权重值来最小化误差,实现对模型的训练和优化。
它是一种灵活、强大的机器学习算法,具有广泛的应用领域,包括图像识别、语音识别、自然语言处理等。
数学建模B P神经网络论文BP 神经网络算法原理:输入信号i x 通过中间节点(隐层点)作用于输出节点,经过非线形变换,产生输出信号k y ,网络训练的每个样本包括输入向量x 和期望输出量d ,网络输出值y 与期望输出值d 之间的偏差,通过调整输入节点与隐层节点的联接强度取值ij w 和隐层节点与输出节点之间的联接强度jk T 以及阈值,使误差沿梯度方向下降,经过反复学习训练,确定与最小误差相对应的网络参数(权值和阈值),训练即告停止。
此时经过训练的神经网络即能对类似样本的输入信息,自行处理输出误差最小的经过非线形转换的信息。
变量定义:设输入层有n 个神经元,隐含层有p 个神经元,输出层有q 个神经元 输入向量:()12,,,n x x x x =隐含层输入向量:()12,,,p hi hi hi hi = 隐含层输出向量:()12,,,p ho ho ho ho = 输出层输入向量:()12,,,q yi yi yi yi = 输出层输出向量:()12,,,q yo yo yo yo =期望输出向量: ()12,,,q do d d d =输入层与中间层的连接权值: ih w 隐含层与输出层的连接权值: ho w 隐含层各神经元的阈值:h b 输出层各神经元的阈值: o b 样本数据个数: 1,2,k m =激活函数: ()f ⋅误差函数:211(()())2qo o o e d k yo k ==-∑算法步骤:Step1.网络初始化 。
给各连接权值分别赋一个区间(-1,1)内的随机数,设定误差函数e ,给定计算精度值ε和最大学习次数M 。
Step2.随机选取第k 个输入样本()12()(),(),,()n x k x k x k x k =及对应期望输出()12()(),(),,()q d k d k d k d k =oStep3.计算隐含层各神经元的输入()1()()1,2,,nh ih i h i hi k w x k b h p ==-=∑和输出()()(())1,2,,h h ho k f hi k h p ==及输出层各神经元的输入()1()()1,2,po ho h o h yi k w ho k b o q ==-=∑和输出()()(())1,2,,o o yo k f yi k o p ==Step4.利用网络期望输出和实际输出,计算误差函数对输出层的各神经元的偏导数()o k δ。
oho o hoyi e e w yi w ∂∂∂=∂∂∂ (())()()pho h o o hh hohow ho k b yi k ho k w w ∂-∂==∂∂∑211((()()))2(()())()(()())f (())()qo o o o o oo oo o o o d k yo k e d k yo k yo k yi yi d k yo k yi k k δ=∂-∂'==--∂∂'=---∑ Step5.利用隐含层到输出层的连接权值、输出层的()o k δ和隐含层的输出计算误差函数对隐含层各神经元的偏导数()h k δ。
()()oo h ho o hoyi e e k ho k w yi w δ∂∂∂==-∂∂∂ 1()()(())()()h ih h ih nih i h h i i ihihhi k e e w hi k w w x k b hi k x k w w =∂∂∂=∂∂∂∂-∂==∂∂∑212121111((()()))()2()()()1((()f(())))()2()()1(((()f(())))()2()()(()())f (())qo o o h h h h qo o o h h h qpo ho h o o h h h h o o o hoo d k yo k ho k e hi k ho k hi k d k yi k ho k ho k hi k d k w ho k b ho k ho k hi k d k yo k yi k w =====∂-∂∂=∂∂∂∂-∂=∂∂∂--∂=∂∂'=--∑∑∑∑1()()(())f (())()qh h qo ho h h o ho k hi k k w hi k k δδ=∂∂'=--∑∑ Step6.利用输出层各神经元的()o k δ和隐含层各神经元的输出来修正连接权值()ho w k 。
1()()()()()ho o h ho N Nho ho o h ew k k ho k w w w k ho k μμδηδ+∂∆=-=∂=+Step7.利用隐含层各神经元的()h k δ和输入层各神经元的输入修正连接权()ih w k 。
1()()()()()()()h ih h i ih h ih N Nih ih h i hi k e e w k k x k w hi k w w w k x k μμδηδ+∂∂∂∆=-=-=∂∂∂=+Step8.计算全局误差。
2111(()())2qm o o k o E d k y k m ===-∑∑Step9.判断网络误差是否满足要求。
当误差达到预设精度或学习次数大于设定的最大次数,则结束算法。
否则,选取下一个学习样本及对应的期望输出,返回到第三步,进入下一轮学习。
算法流程图:参数确定:确定了网络层数、每层节点数、传递函数、初始权系数、学习算法等也就确定了BP网络。
确定这些选项时有一定的指导原则,但更多的是靠经验和试凑。
1. 样本数据采用BP 神经网络方法建模的首要和前提条件是有足够多典型性好和精度高的样本。
而且,为监控训练(学习)过程使之不发生“过拟合”和评价建立的网络模型的性能和泛化能力,必须将收集到的数据随机分成训练样本、检验样本(10%以上)和测试样本(10%以上)3部分。
2.输入/输出变量一般地,BP 网络的输入变量即为待分析系统的内生变量(影响因子或自变量)数,一般根据专业知识确定。
若输入变量较多,一般可通过主成份分析方法压减输入变量,也可根据剔除某一变量引起的系统误差与原系统误差的比值的大小来压减输入变量。
输出变量即为系统待分析的外生变量(系统性能指标或因变量),可以是一个,也可以是多个。
一般将一个具有多个输出的网络模型转化为多个具有一个输出的网络模型效果会更好,训练也更方便。
3.数据的预处理由于BP 神经网络的隐层一般采用Sigmoid 转换函数,为提高训练速度和灵敏性以及有效避开Sigmoid 函数的饱和区,一般要求输入数据的值在0~1之间。
因此,要对输入数据进行预处理。
一般要求对不同变量分别进行预处理,也可以对类似性质的变量进行统一的预处理。
如果输出层节点也采用Sigmoid 转换函数,输出变量也必须作相应的预处理,否则,输出变量也可以不做预处理。
但必须注意的是,预处理的数据训练完成后,网络输出的结果要进行反变换才能得到实际值。
再者,为保证建立的模型具有一定的外推能力,最好使数据预处理后的值在0.2~0.8之间。
标准化:minmax mind d d d d αβ-'=⨯+-4.隐层数一般认为,增加隐层数可以降低网络误差,提高精度,但也使网络复杂化,从而增加了网络的训练时间和出现“过拟合(overfitting)” 造成网络的性能脆弱,泛化能力(generalization ability)下降。
Hornik 等早已证明:若输入层和输出层采用线性转换函数,隐层采用Sigmoid 转换函数,则含一个隐层的MLP 网络能够以任意精度逼近任何有理函数。
显然,这是一个存在性结论。
在设计BP 网络时可参考这一点,应优先考虑3层BP 网络(即有1个隐层)。
图 三层BP 网络的拓扑结构5.隐层节点数在BP 网络中,若隐层节点数太少,网络可能根本不能训练或网络性能很差;若隐层节点数太多,虽然可使网络的系统误差减小,但一方面使网络训练时间延长,另一方面,训练容易陷入局部极小点而得不到最优点,也是训练时出现“过拟合”的内在原因,但是目前理论上还没有一种科学的和普遍的确定方法。
为尽可能避免训练时出现“过拟合”现象,保证足够高的网络性能和泛化能力,确定隐层节点数的最基本原则是:在满足精度要求的前提下取尽可能紧凑的结构,即取尽可能少的1x 2x 1Nx隐层节点数。
因此,合理隐层节点数应在综合考虑网络结构复杂程度和误差大小的情况下用节点删除法和扩张法确定。
6.传递函数图BP网络常用的传递函数BP网络的传递函数有多种。
Log-sigmoid型函数的输入值可取任意值,输出值在0和1之间;tan-sigmod型传递函数tansig的输入值可取任意值,输出值在-1到+1之间;线性传递函数purelin的输入与输出值可取任意值。
BP网络通常有一个或多个隐层,该层中的神经元均采用sigmoid型传递函数,输出层的神经元则采用线性传递函数,整个网络的输出可以取任意值。
7.学习率学习率影响系统学习过程的稳定性。
大的学习率可能使网络权值每一次的修正量过大,甚至会导致权值在修正过程中超出某个误差的极小值呈不规则跳跃而不收敛;但过小的学习率导致学习时间过长,不过能保证收敛于某个极小值。
所以,一般倾向选取较小的学习率以保证学习过程的收敛性(稳定性),通常在0.01~0.8之间。
8.网络的初始连接权值BP算法决定了误差函数一般存在(很)多个局部极小点,不同的网络初始权值直接决定了BP算法收敛于哪个局部极小点或是全局极小点。
因此,要求计算程序必须能够自由改变网络初始连接权值。
由于Sigmoid转换函数的特性,一般要求初始权值分布在-0.5~0.5之间比较有效。
10.收敛误差界值Emin在网络训练过程中应根据实际情况预先确定误差界值。
误差界值的选择完全根据网络模型的收敛速度大小和具体样本的学习精度来确定。
当Emin 值选择较小时,学习效果好,但收敛速度慢,训练次数增加。
如果Emin值取得较大时则相反。
网络模型的性能和泛化能力:训练神经网络的首要和根本任务是确保训练好的网络模型对非训练样本具有好的泛化能力(推广性),即有效逼近样本蕴含的内在规律,而不是看网络模型对训练样本的拟合能力。
判断建立的模型是否已有效逼近样本所蕴含的规律, 主要不是看测试样本误差大小的本身,而是要看测试样本的误差是否接近于训练样本和检验样本的误差。
非训练样本误差很接近训练样本误差或比其小,一般可认为建立的网络模型已有效逼近训练样本所蕴含的规律,否则,若相差很多(如几倍、几十倍甚至上千倍)就说明建立的网络模型并没有有效逼近训练样本所蕴含的规律,而只是在这些训练样本点上逼近而已,而建立的网络模型是对训练样本所蕴含规律的错误反映。
算法的特点:1.非线性映照能力。