等效平衡专题小结

等效平衡一、概念在一定条件（恒温恒容或恒温恒压）下，同一可逆反应体系,不管是从正反应开始，还是从逆反应开始，在达到化学平衡状态时，任何相同组分的含量(体积分数、物质的量分数等）均相同,这样的化学平衡互称等效平衡（包括“相同的平衡状态”).概念的理解:（1）外界条件相同：通常可以是①恒温、恒容，②恒温、恒压。

（2）“等效平衡”与“完全相同的平衡状态”不同：“完全相同的平衡状态”是指在达到平衡状态时,任何组分的物质的量分数(或体积分数）对应相等，并且反应的速率等也相同，但各组分的物质的量、浓度可能不同.而“等效平衡”只要求平衡混合物中各组分的物质的量分数（或体积分数)对应相同，反应的速率、压强等可以不同。

(3）平衡状态只与始态有关，而与途径无关，(如：①无论反应从正反应方向开始,还是从逆反应方向开始②投料是一次还是分成几次③反应容器经过扩大—缩小或缩小—扩大的过程，）只要起始浓度相当,就达到相同的平衡状态.二、等效平衡的分类在等效平衡中比较常见并且重要的类型主要有以下三种：I类：恒温恒容下对于反应前后气体体积发生变化的反应来说（即△V≠0的体系）：等价转化后，对应各物质起始投料的物质的量与原平衡起始态相同。

II类：恒温恒容下对于反应前后气体体积没有变化的反应来说(即△V=0的体系)：等价转化后,只要反应物（或生成物）的物质的量的比例与原平衡起始态相同，两平衡等效。

III类：恒温恒压下对于气体体系等效转化后，只要反应物（或生成物）的物质的量的比例与原平衡起始态相同，两平衡等效。

解题的关键,读题时注意勾画出这些条件，分清类别,用相应的方法求解.我们常采用“等价转换”的方法，分析和解决等效平衡问题三、例题解析I类：在恒温恒容下,对于化学反应前后气体体积发生变化的可逆反应，只改变起始加入物质的物质的量，如果通过可逆反应的化学计量数之比换算成化学方程式的同一边物质的物质的量与原平衡相同，则两平衡等效.例1：在一定温度下，把2 mol SO2和1 mol O2通入一定容积的密闭容器中,发生如下反应，,当此反应进行到一定程度时反应混合物就处于化学平衡状态。

等效平衡知识总结一、等效平衡原理的建立化学平衡理论指出：同一可逆反应，当外界条件相同时，反应不论是从正方应开始，还是从逆反应开始，或者从正、逆反应同时开始，最后都能达到平衡状态。

化学平衡状态与条件有关，而与建立平衡的途径无关。

因此，我们把：在一定条件（恒温、恒压或怛温、恒容）下，只是起始物质加入情况不同的同一可逆反应达到平衡后，反应混合物中各组分的百分数（体积、物质的量、质量）均对应相等，这样的化学平衡互称等效平衡。

切记的是：组分的百分数相同，包括体积分数、物质的量分数或质量百分数，而不仅仅是指浓度相同，因为同一组分百分数相同时其浓度不一定相等。

概念的理解：（1）外界条件相同：通常可以是①恒温、恒容; ②恒温、恒压。

（2）“等效平衡”与“完全相同的平衡状态”不同：“完全相同的平衡状态”是指在达到平衡状态时，任何组分的物质的量分数（或体积分数）对应相等，并且反应的速率等也相同，但各组分的物质的量、浓度可能不同。

而“等效平衡”只要求平衡混合物中各组分的物质的量分数（或体积分数）对应相同，反应的速率、压强等可以不同。

（3）平衡状态只与终态有关，而与途径无关，（如：①无论反应从正反应方向开始，还是从逆反应方向开始②投料是一次还是分成几次③反应容器经过扩大—缩小或缩小—扩大的过程，）只要起始浓度相当，就达到相同的平衡状态。

判断“等效平衡”的方法（1）使用极限转化的方法将体系转化成同一方向的反应物或生成物。

（2）观察有关物质的量是否相等或成比例。

等温等容：A、m+n≠p+q 相同起始物质的物质的量相等B、m+n = p+q 相同起始物质的物质的量之比相等等温等压：相同起始物质的物质的量之比相等。

等压比相等，等容量相等。

但若系不变，可为比相等。

a.气态物质反应前后体积变化的可逆反应Ⅰ：恒温恒容时1.建立等效平衡的条件是：反应物的投料相当即“等量”加入2.判断方法：“一边倒”的极限转换法即将不同的投料方式根据化学方程式中计量系数比换算到同一边时，如果反应物（或生成物）中同一组分的物质的量完全相同，则互为等效平衡。

等效平衡原理及规律总结1. 什么是等效平衡原理？等效平衡原理，听起来是不是有点高大上？其实它的意思就是把复杂的事情简化，找到两者之间的平衡点，就像我们平常说的“各取所需”。

咱们生活中常常会遇到这样的情况，比如说，朋友之间互相借东西，彼此之间都希望能够不亏。

这个原则在科学、经济甚至人际关系中都能找到身影。

1.1 这个原理在科学里是怎么用的呢？我们常常看到物理公式，比如力、能量这些东西，都是在寻找一种平衡状态。

就好比一辆车在行驶时，前后、左右的力要均衡，不然可就容易翻车了。

1.2 在经济学上，等效平衡原理也大显身手。

市场供需关系就是个经典案例，需求上去了，价格就跟着涨，供给上去了，价格又会掉。

人们在这场“博弈”中追求一种心理上的平衡，就像玩游戏，必须找准自己的位置才能赢。

2. 等效平衡的应用实例说到这儿，大家可能会问，这个原理具体应用在哪儿呢？别急，我这就给你讲几个生动的例子。

2.1 比如说，家庭日常开支。

大家都知道，家庭开支就像是一个大锅，锅里要放什么材料，放多少，得讲究讲究。

如果每个月工资都用来吃喝玩乐，那没几天就得喝西北风。

为了保持家里的“经济平衡”，咱们得合理规划支出，把钱用在刀刃上，这样才能“财源滚滚来”。

2.2 再说说职场上的事情。

你可能听过“工作与生活平衡”这个词，实际上就是在说等效平衡原理。

工作上拼命加班，结果身体累得像个瘫，生活中也没啥乐趣。

咱们要做到工作与生活两手抓，才能活得开心，这样才能长久。

3. 等效平衡的规律接下来，我们聊聊等效平衡原理的几个小规律。

虽然名字听起来像科学家发明的，但其实很接地气。

3.1 第一个规律是“均衡取舍”。

在任何情况下，都得学会放下点东西，才能得到更多。

比如你在选择工作时，可能要在高薪和兴趣之间做出取舍。

要是总想把所有的好处都捞到手，那最后可能啥都没了。

3.2 第二个规律是“动态平衡”。

就像骑自行车一样，如果不往前走，那就很容易摔倒。

生活中也是，环境在变化，我们的选择也要不断调整，才能保持平衡。

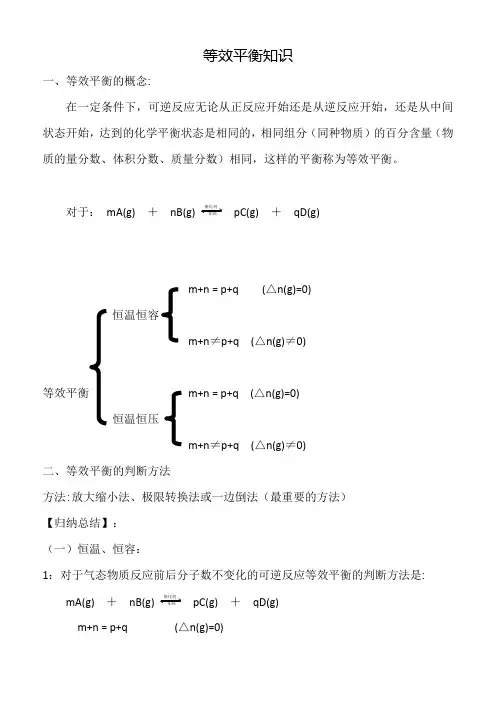
等效平衡知识一、等效平衡的概念:在一定条件下，可逆反应无论从正反应开始还是从逆反应开始，还是从中间状态开始，达到的化学平衡状态是相同的，相同组分（同种物质）的百分含量（物质的量分数、体积分数、质量分数）相同，这样的平衡称为等效平衡。

对于：mA(g) ＋nB(g) 催化剂加热pC(g) ＋qD(g)m+n = p+q (△n(g)=0)恒温恒容m+n≠p+q (△n(g)≠0)等效平衡m+n = p+q (△n(g)=0)恒温恒压m+n≠p+q (△n(g)≠0)二、等效平衡的判断方法方法:放大缩小法、极限转换法或一边倒法（最重要的方法）【归纳总结】：（一）恒温、恒容：1：对于气态物质反应前后分子数不变化的可逆反应等效平衡的判断方法是: mA(g) ＋nB(g) 催化剂加热pC(g) ＋qD(g)m+n = p+q (△n(g)=0)使用极限转化的方法将各种情况变换成同一反应物或生成物，然后观察有关物质的物质的量比是否相等。

若相等各组分百分量相同，n 、c 同比例变化，则为等效平衡2：对于气态物质反应前后分子数有变化的可逆反应等效平衡的判断方法是:mA(g) ＋ nB(g) 催化剂加热 pC(g) ＋ qD(g)m+n ≠p+q (△n(g)≠0)使用极限转化的方法将各种情况变换成同一反应物或生成物，然后观察有关物质的物质的量是否对应完全相等。

若相等各组分百分量、n 、c 均相同，则为等效平衡（等同平衡）例1、恒温恒容时对于反应：H2(g) + I2(g) 催化剂加热 2HI(g)下列条件能与下图达到等效平衡的是（ ）A. 2 mol HIB. 2 mol H 2+2 mol I 2C. 1 mol H2+1 mol I 2+2 mol HID. 0.5 mol H 2+0.5 mol I 2+1 mol HI例2：在一个1L 的密闭容器中，加入2molA 和1molB ，发生下述反应： 2A(g)+B(g) 催化剂加热 3C(g)+D(s) 达到平衡时， C 的浓度为1.2mol/L 。

等效平衡知识点总结等效平衡是指在特定条件下，两个或多个物体或系统的状态达到平衡，其效果相同。

等效平衡是物理学中一个重要的概念，它在多个领域都有着广泛的应用，例如力学、热力学、电磁学等。

在本文中，我们将对等效平衡的知识点进行总结，包括概念、原理、应用等方面。

1. 概念等效平衡是指在某些条件下，两个或多个物体或系统的状态达到平衡，而它们的效果是相同的。

也就是说，虽然系统的组成部分、结构或者形状不同，但是它们达到平衡的效果却是一样的。

这种情况下，我们可以认为这些系统是等效平衡的。

2. 原理等效平衡的原理可以总结为以下几点：（1）平衡条件：等效平衡的系统必须满足平衡条件，即各个部分的作用力和反作用力平衡，或者各个部分的力矩和反力矩平衡。

只有在这种条件下，系统才能达到平衡状态。

（2）效果相同：虽然系统的组成部分、结构和形状可能有所不同，但是它们达到平衡的效果是相同的。

这意味着我们可以从效果上来看，将这些系统视为等效平衡的。

（3）等效性：等效平衡的系统之间具有等效性，即它们在某些特定条件下可以互相替代，而不会改变系统的平衡状态。

这种等效性是等效平衡的重要特征。

3. 应用等效平衡在物理学中有着广泛的应用，包括但不限于以下方面：（1）力学：在力学中，我们常常会遇到复杂的物体或系统，如梁、桥、支架等。

通过等效平衡的原理，我们可以将这些复杂的系统简化为等效的力学模型，从而更容易地进行分析和计算。

（2）热力学：在热力学中，等效平衡的概念可以用来分析热量的传递和平衡。

例如，当两个系统之间存在热传导时，我们可以将它们视为等效平衡的系统，从而更好地理解热传导的规律。

（3）电磁学：在电磁学中，等效平衡的概念可以用来分析电路的平衡和稳定性。

例如，我们可以将复杂的电路简化为等效的电路模型，从而更方便地进行电路设计和分析。

4. 注意事项在使用等效平衡的原理时，需要注意以下几点：（1）条件限制：等效平衡的原理只在特定条件下成立。

因此，在使用等效平衡的原理时，需要确保系统满足平衡条件，才能将其视为等效平衡的。

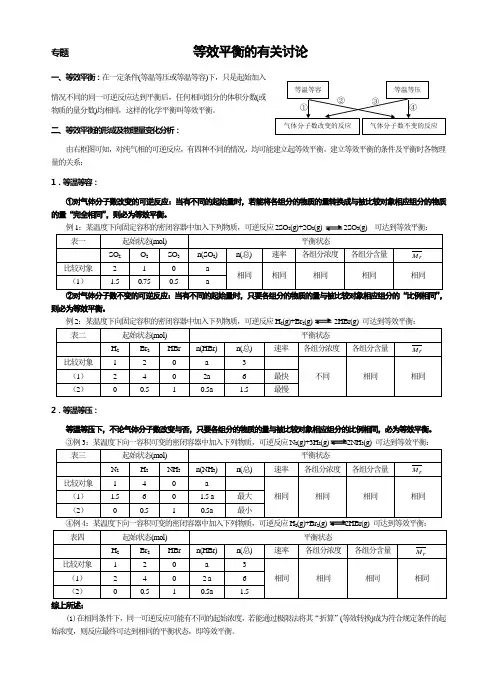
专题 等效平衡的有关讨论一、等效平衡：在一定条件(等温等压或等温等容)下，只是起始加入情况不同的同一可逆反应达到平衡后，任何相同组分的体积分数(或物质的量分数)均相同，这样的化学平衡叫等效平衡。

二、等效平衡的形成及物理量变化分析：由右框图可知，对纯气相的可逆反应，有四种不同的情况，均可能建立起等效平衡。

建立等效平衡的条件及平衡时各物理量的关系： 1．等温等容：①对气体分子数改变的可逆反应：当有不同的起始量时，若能将各组分的物质的量转换成与被比较对象相应组分的物质的量“完全相同”，则必为等效平衡。

例1：某温度下向固定容积的密闭容器中加入下列物质，可逆反应2SO②对气体分子数不变的可逆反应：当有不同的起始量时，只要各组分的物质的量与被比较对象相应组分的“比例相同”，则必为等效平衡。

例2：某温度下向固定容积的密闭容器中加入下列物质，可逆反应H (g) 2．等温等压：等温等压下，不论气体分子数改变与否，只要各组分的物质的量与被比较对象相应组分的比例相同，必为等效平衡。

③例3：某温度下向一容积可变的密闭容器中加入下列物质，可逆反应N (g) 2NH ④例4：某温度下向一容积可变的密闭容器中加入下列物质，可逆反应H 2HBr(g) 综上所述：(1)在相同条件下，同一可逆反应可能有不同的起始浓度，若能通过极限法将其“折算”(等效转换)成为符合规定条件的起始浓度，则反应最终可达到相同的平衡状态，即等效平衡。

(2)建立等效平衡的条件：(Ⅰ)等温等容下的气体分子数改变的可逆反应：若各组分的量能转换成与被比较对象相应组分的量“完全相同”，则可达到等效平衡。

(如：情况①)(Ⅱ)等温等容下的气体分子数不变的可逆反应、等温等压下的气相可逆反应(无论分子数改变与否)：只要各组分物质的量与被比较对象相应组分的量“比例相同”，则可达到等效平衡。

(如情况②、③、④)(3) 等效平衡时各物理量的关系：等效平衡下混合物各组分的体积分数(或物质的量分数、相对平均分子质量) 一定相同。

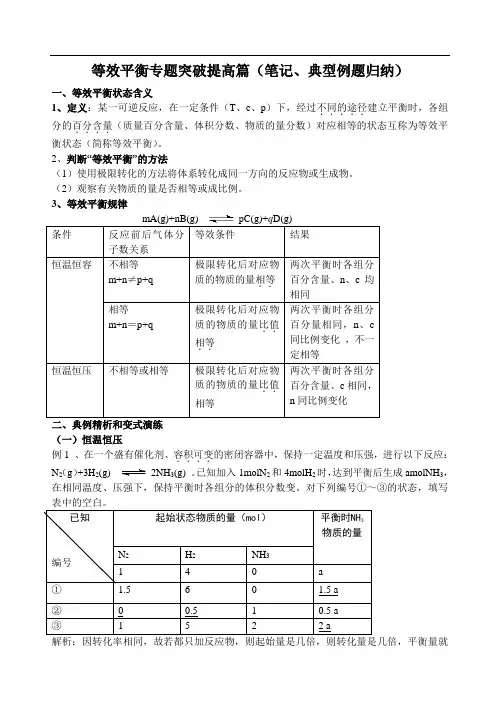
等效平衡专题突破提高篇（笔记、典型例题归纳）一、等效平衡状态含义1、定义：某一可逆反应，在一定条件（T 、c 、p ）下，经过不同的途径．．．．．建立平衡时，各组分的百分含量．．．．（质量百分含量、体积分数、物质的量分数）对应相等的状态互称为等效平衡状态（简称等效平衡）。

2、判断“等效平衡”的方法（1）使用极限转化的方法将体系转化成同一方向的反应物或生成物。

（2）观察有关物质的量是否相等或成比例。

3、等效平衡规律二、典例精析和变式演练（一）恒温恒压例1 、在一个盛有催化剂、容积可变．．．．的密闭容器中，保持一定温度和压强，进行以下反应： N 2（g ）+3H 2(g) 2NH 3(g) 。

已知加入1molN 2和4molH 2时，达到平衡后生成amolNH 3，在相同温度、压强下，保持平衡时各组分的体积分数变。

对下列编号①～③的状态，填写表中的空白。

解析：因转化率相同，故若都只加反应物，则起始量是几倍，则转化量是几倍，平衡量就是几倍，又因等压条件下物质的量之比等于体积之比，故起始量之比等于平衡量之比。

①和题干量之比是1.5，平衡之比就是1.5。

②的平衡量是题干平衡量的一半，则若没有NH3，只有N2、H2，则其物质的量应分别为0.5和2mol，又因1 mol NH3完全转化生成N20.5 mol，H21.5mol，故原来的N2、H2分别为0 mol 和0.5mol。

③可同理推得。

例2、恒温、恒压．．下，在一个可变容积的容器中发生如下发应：A（g）＋B（g）C（g）（1）若开始时放入1molA和1molB，到达平衡后，生成a molC，这时A的物质的量为mol。

（2）若开始时放入3molA和3molB，到达平衡后，生成C的物质的量为mol。

（3）若开始时放入x molA，2molB和1molC，到达平衡后，A和C的物质的量分别是ymol 和3a mol，则x＝mol，y＝mol。

平衡时，B的物质的量（选填一个编号）（甲）大于2 mol （乙）等于2 mol（丙）小于2 mol （丁）可能大于、等于或小于2mol作出此判断的理由是。

化学平衡小结——等效平衡问题一、概念在一定条件（恒温恒容或恒温恒压）下，同一可逆反应体系，不管是从正反应开始，还是从逆反应开始，在达到化学平衡状态时，任何相同组分的百分含量．．．．（体积分数、物质的量分数等）均相同，这样的化学平衡互称等效平衡（包括“全等等效和相似等效”）。

概念的理解：（1）只要是等效平衡，平衡时同一物质的百分含量．．．．（体积分数、物质的量分数等）一定相同（2）外界条件相同：通常可以是①恒温、恒容，②恒温、恒压。

（3）平衡状态只与始态有关，而与途径无关，（如：①无论反应从正反应方向开始，还是从逆反应方向开始②投料是一次还是分成几次③反应容器经过扩大—缩小或缩小—扩大的过程，）比较时都运用“一边倒”．．．．．．．．进行比较。

．．．．．倒回到起始的状态二、等效平衡的分类在等效平衡中比较常见并且重要的类型主要有以下二种：I类：全等等效——不管是恒温恒容．．用量．．．．．．．。

只要“一边倒”倒后各反应物起始．．．．还是恒温恒压是一致的．．．．就是全等等效“全等等效”平衡除了满足等效平衡特征[转化率相同，平衡时百分含量（体积分数、物质的量分数）一定相等]外还有如下特征“．一边倒．．．．．．．．．．．．．也．．．物质的量相等，平衡物质的量．．．”．后．同．物质的．．．起始一定相等．．．．。

．拓展与延伸：在解题时如果要求起始“物质的量相等”或“平衡物质的量相等”字眼的肯定是等效平衡这此我们只要想办法让起始用量相等就行例1．将6molX和3molY的混合气体置于密闭容器中，发生如下反应：2X (g)+Y(g)2Z (g)，反应达到平衡状态A时，测得X、Y、Z气体的物质的量分别为1.2mol、0.6mol和4.8mol。

若X、Y、Z的起始物质的量分别可用a、b、c表示，请回答下列问题：（1）若保持恒温恒容，且起始时a=3.2mol，且达到平衡后各气体的体积分数与平衡状态A 相同，则起始时b、c的取值分别为，。

专题一、等效平衡问题1、定义：在相同条件下定温定容或定温定压,对同一可逆反应,由于起始有关物质的量“相当”,无论从正反应开始还是从逆反应开始,均可达到平衡,且任何组分的含量通常为百分含量相同,这样的平衡互称为等效平衡;2、等效平衡的类型及建立等效平衡的条件规律一: 恒．温．恒．容．条件下,对于任何．．．．,如．．无论反应前后气体分子数是否相同可逆反应果起始加入物质的物质的量不同,按化学方程式中的化学计量关系换算成同一方向的物质即“一边倒”后,各组分的物质的量与原平衡相同,则两平衡等效,平衡时,同种组分的体积分数、物质的量浓度、物质的量均相同也可叫全等平衡;如: mAg+nBg pCg+qDg起始① mmol nmol 0 0起始② 0 0 pmol qmol上述两种情况投料不同,但是将②中投料“左边倒”后,四种物质的物质的量均同①相同,因此两种情况可达到等效平衡,平衡时,同种组分如A的体积分数、物质的量浓度、物质的量均相同;例1.在一固定体积的密闭容器中通入2molA和1molB发生反应2Ag+Bg3Cg+Dg反应达到平衡时,测得C的物质的量浓度为wmol/L.若维持容器的容积不变,按下列四种配比做起始浓度,达平衡后,C的浓度仍维持wmol/L的是A、4molA+2molBB、2molA+1molB+3molC+1molDC、3molC+1molD+1molBD、3molC+1molD例2、在固定体积的密闭容器中,加入2molA,1molB,发生反应：Ag+Bg 2Cg达到平衡时,C 的质量分数为ω%,在相同条件下按下列情况充入物质达到平衡时C的质量分数仍为ω%的是,2molB ,2molC例3、在一个固定体积的密闭容器中,保持一定浓度,进行以下反应：4Ag+5Bg 4Cg+6Dg,已知加入4molA和5molB时,反应进行到一定程度时,反应混合物就处于平衡状态,现在该容器中,保持温度不变,令a,b,c,d分别代表初始加入的A,B,C,D的物质的量,如果a,b,c,d取不同的数值,它们必须满足一定关系,才能保证达到平衡时,反应混合物中几种物质的百分含量仍跟上述平衡时完全相同,请填写下列空白：1若a=0,b=0, 则c= ,d= .2若a=1,则b= ,c= ,d=3a,b,c,d取值必须满足的一般条件是请用方程式表示,其中一个只含a和c,另一个只含b 和c: , .规律二: 恒温恒．．．压．条件下,对于任何．．无论反应前后气体分子数是否相同可逆反应．．．．,如果起始加入物质的物质的量不同,按化学方程式中的化学计量关系“一边倒”后, 各组分的物质的量之比与原平衡相同,则两平衡等效,平衡时,同种组分的体积分数、物质的量浓度相同,但物质的量不同;如: mAg + nBg pCg + qDg起始① mmol nmol 0 0起始② 0 0起始③上述三种情况投料不同,但②③两种情况“左边倒”后,nA 和nB 的比值均同①相同,因此三种情况可达到等效平衡,平衡时,同种组分如A 的体积分数、物质的量浓度相同,但物质的量不同;例4．恒温恒压下,在一个可变容积的密闭容器中发生如下反应： Ag+Bg Cg开始时放入1molA 和1molB,达到平衡后,生成amolC.1若开始时放入3molA 和3molB,达到平衡后,生成C 的物质的量为 mol2若开始时放入xmolA 、3molB 和1molC,达到平衡后,A 和C 的物质的量分别是ymol 和3amolx= ,y=规律三: 恒温恒容．．．．条件下,对于反应前后气体分子数相同．．．．．．．．．．．的可逆反应,如果起始加入物质的物质的量不同,按化学方程式中的化学计量关系“一边倒”后, 各组分的物质的量之比与原平衡相同,则两平衡等效,平衡时,同种组分的体积分数相同,但物质的量浓度、物质的量不同;如：H2g + I2g 2HIg起始① 1mol 1mol 0 起始② 0 0 4mol 起始③ 0上述三种情况投料不同,但将②中投料“左边倒”后三种情况下nH2和nI2的比值相同,②可认为①容积减半压强加倍得到,③可认为容积加倍压强减半得到,压强改变平衡不移动,所以三种情况可达等效平衡;三种情况达到平衡时,同种组分如H2的体积分数相同,物质的量及物质的量浓度不相同;例5.有甲、乙两个容积相等的恒容密闭容器,向甲容器中通入6molA和2molB,向乙容器中通入、和3molC,将两容器的温度恒定在770K,使反应3Ag+Bg xCg达到平衡,此时测得甲、乙两容器中C的体积分数都是,试回答下列有关问题：1若平衡时,甲、乙两容器中A的物质的量不相等,则x= ；若平衡时甲、乙两容器中A的物质的量不相等,则x= .2平衡时,甲、乙两容器中A、B的物质的量之比是否相等填“相等”或“不相等”,平衡时甲中A的体积分数为3若平衡时两容器中的压强不相等,则两容器中压强之比为3、等效平衡的解题思路1分析是否属于等效平衡问题 2属何种类型的等效平衡3选择建立平衡的条件极值法练习1.在t℃时,向一容积不变的密闭容器内放入1molA和1molB,发生如下反应：Ag+Bg Cg+2Dg.达到平衡时C的含量m%,保持温度不变,若按下列配比将物质放入容器中,达到平衡时,C的含量仍为m%的是和2molB ,1molA和1molB和2molD 和1molD2. 在一定条件下,向一带活塞的密闭容器内充入2molSO2和1molO2,发生下列反应：2 SO2 g+O2g2SO3g,达到平衡后改变下列条件,SO3气体平衡浓度不改变的是A.保持温度和容器体积不变,充入1mol SO3B. 保持温度和容器压强不变,充入1mol SO3C. 保持温度和容器压强不变,充入1mol O2D. 保持温度和容器压强不变,充入1mol Ar3.恒温恒容下,有反应2Ag + 2Bg Cg + 3Dg,现从两条途径分别建立平衡;途径I：A、B 的起始浓度均为2mol/L;途径II：C、D起始浓度分别为2mol/L和6mol/L,下列叙述错误的是A.平衡时,体系内混合气体的百分组成相同B.平衡时,途径I所得各组分浓度为途径II所得各组分浓度的一半C.平衡时,途径I 的反应速率vA等于途径II的反应速率vAD.平衡时,途径I所得混合气体密度为途径II所得混合气体密度的一半3.在一恒定的容器中充入2molA和1molB发生反应：2Ag+Bg xCg达到平衡后,C的体积分数为a%;若维持容器的容积和温度不变,按起始物质的量A为, B为, C为充入容器中,达到平衡后,C的体积分数仍为a%,则x的值为A.只能为2B.只能为3C.可能为2,也可能为3D.任意值4.Ⅰ.在一个固定体积的密闭容器中2molA和1molB发生反应2Ag+Bg3Cg +Dg, 达到平衡时,C的浓度为Wmol/L维持容器体积和温度不变,按下列四种配比作为起始物质,达到平衡后,若C的浓度仍为Wmol/L,该配比是+2molB +1molD+1molB+2molA +1molD+1molB +1molDⅡ.①若题中改为1molA,,,作为起始物质,达到平衡后,C的浓度是否仍为Wmol/L②若题中A为L,B为,则C为mol,D为 mol作为起始物质时,达到平衡后,C的浓度仍为Wmol/L.③若题中改为amolA,bmolB,cmolC,dmolD作为起始物质,达到平衡后,C的浓度如果仍为Wmol/L,则a与c,b与d分别满足什么关系：、5.Ⅰ.恒温恒压下,在一个可变容积的容器中发生如下反应：Ag+Bg Cg1若开始时放入1molA和1molB,到达平衡后,生成amolC,这时A的物质的量为 mol. 2若开始时放入3molA和3molB,到达平衡后,生成C的物质的量为 mol.3若开始时放入xmolA,2molB和1molC,到达平衡后,A和C的物质的量分别是ymol和3amol,则x= mol,y= mol.平衡时,B的物质的量选一个编号甲大于2mol 乙等于2mol丙小于2mol 丁可能大于、等于或小于2mol作出此判断的理由是（1）若在3的平衡混合物中再加入3molC,待再次到达平衡后,C的物质的量分数是Ⅱ.若维持温度不变在一个与1反应前起始体积相同、且容积固定的容器中发生上述反应;（2）开始时放入1molA和1molB到达平衡后生成bmolC,将b与1小题中的d进行比较选一个编号甲a<b 乙a>b 丙a=b 丁不能比较a和b的大小作出判断的理由是专题二、化学平衡问题的解题技巧及规律一、当外界条件改变引起多方面因素发生改变时,可以通过构造一个中间状态来解题,思维模式为：例1：一真空密闭容器中盛有1molPCl5,加热到20℃时发生如下反应：PCl5g PCl3g+ Cl2g反应达到平衡时,PCl5所占体积分数为M%,若在同一温度和同一容器中最初投入的是2molPCl5,反应达到平衡时 PCl5所占的体积分数为N%,则M和N的正确关系是>N <N =N D.无法比较例2：一定温度下,在容积固定的密闭容器中发生可逆反应2Ag Bg并达到平衡,在相同条件下,若分别再向容器中通入一定量的气体A或气体B,重新达到平衡后,容器内A的体积分数与原平衡相比A.都减小B.前者增大,后者减小C.都增大D.前者减小,后者增大练习1：某温度下,在固定容积的密闭中,可逆反应Ag+3Bg2Cg达到平衡,测得平衡时A,B,C物质的量之比nA:nB:ng=2:2:1,若温度保持不变,以2:2:1的物质的量之比再充入A,B 和C,下列判断中正确的是A.平衡向逆反应方向移动B.平衡不发生移动C. C 的质量分数增大D. C的质量可能减小练习2：某温度下,在一容积可变的容器中,反应2Ag+Bg2Cg达到平衡时,A,B,C的物质的量分别为4mol,2mol和4mol,保持温度和压强不变,对平衡混合物中三者的物质的量做如下调整,可使平衡右移的是A.均减半B.均加倍C.均增加1molD.均减少1mol练习3：在一密闭容器中,反应aAg bBg达平衡后,保持温度不变,将容器体积增大一倍,当达到新的平衡时B的浓度是原来的60%,则A.平衡向正反应方向移动了B.物质A的转化率减小了C.物质B的质量分数增加了 >b练习4:有两只密闭容器A和B,A容器有一个可移动活塞使容器内保持恒压,B容器保持恒容,起始时向两只容器中分别充入等量的体积比为2∶1的SO2和O2的混合气体,并使A和B容积相等.在保持400℃条件下使之发生反应:2SO2 +O22SO3,填写下列空白:1达到平衡所需时间A比B ,A中的SO2转化率比B .2达到1 所述平衡后,若向两容器通入数量不多的等量氩气,A容器的化学平衡移动,B容器的化学平衡移动.3达到1所述平衡后,向两容器中通入等量的原反应气体,达到平衡后,A中的SO3体积分数增大、减小、不变,B中的SO3体积分数练习5:在373K,把气体通入体积为500ml的真空密闭容器中立即出现红棕色,反应进行到2s时,NO2含量为,进行到60s时,达到平衡,此时容器内混合气体的密度是氢气密度的倍,则下列叙述中正确的是A.开始2s内CN2O4的变化表示的反应速率为L-1s-1B.达到平衡时体系内压强是开始时的倍C.平衡时CN2O4为 L-1D.平衡后若压缩容器,减小体积,则再达平衡时NO2浓度下降二、平衡正向移动与反应物的转化关系1.由于温度或压强改变而引起平衡正向移动时,反应物的转化率必定增大;2.由于增加反应物浓度引起平衡正向移动时,有以下几种情况：1对于反应物不考虑固体反应物不只一种的可逆反应,如N2+3H22NH3,平衡时增加一种反应物浓度,平衡正向移动,另一种反应物的转化率增大,而自身的转化率却减小;2对于反应物只有一种的可逆反应并规定起始时只有反应物,若反应前后气体分子数不变,如2HIg H2g+I2g,则无论增大或减小HI的浓度,HI的转化率都不改变,若反应后气体分子数减少,如2NO2g N2O4g,则增大NO2的浓度,NO2的转化率增大；若反应后气体分子数增大,如2NH3N2+3H2,则增大 NH3的浓度,NH3的转化率减小;专题三、化学平衡图象题的解法1.步骤：①一看面即纵坐标与横坐标的意义,二看线即线的走向和趋势,三看点即起点、折点、交点、终点,四看辅助线如等温线、等压线、平衡线等,五看量的变化如浓度变化,温度变化,转化率变化等;②想规律：联想外界条件的改变对化学反应速率和化学平衡的影响规律;③作判断：根据图象中表现的关系与所学规律相比较,作出符合题目要求的判断;2.原则：①“定一议二”②“先拐先平”例1.在一密闭体系中发生下列反应:N2g+3H2g2NH3g正反应放热,下图是某一时间段中反应速率与反应进程的曲线关系图.回答下列问题: 1处于平衡状态的时间段是2t1, t3, t4时刻体系中分别是什么条件发生了变化 t1: t3: t4:3下列各时间段时,氨的体积分数最高的是A. t0~t1B. t2~t3C. t3~t4D. t5~t6例g+nBg qCg反应在密闭容器中进行,如图表示反应过程中温度T,压强P与B%气体B在混合气体中的百分含量的关系曲线由曲线分析,下列结论正确的是+n>q 正反应为放热反应 +n>q 正反应为吸热反应+n<q正反应为放热反应 +n<q 正反应为吸热反应例3.某一达到化学平衡状态的可逆反应：mAg+nBg pCg + qDg,如图表示A的转化率αA与温度,压强的关系,分析该图示可以得出的结论是A. 正反应吸热,m+n>p+qB. 正反应吸热,m+n<p+qC. 正反应放热,m+n>p+qD. 正反应放热,m+n<p+q例4.可逆反应nXg+Yg mZg正反应为放热反应的x%x%为x混合气体中的体积分数与温度关系如右图所示,图中曲线上a,d点是代表平衡时x%与温度关系的两点,b,c两点是反应混合物未平衡时的两点,若研究与密闭容器中以定压进行反应,当V正>V逆时,则在右图中,表示此种情况下的点是点;例5.反应mAg +nBg pCg+qDg,开始充入A,B或C,D,下图一,图二分别表示反应达到平衡后,改变温度、压强对反应速率及平衡的影响,下列判断正确的是A.开始时充入A、B,m+n>p+q,正反应为放热反应B. 开始时充入A、B,m+n<p+q,正反应为吸热反应C. 开始时充入C、D,m+n>p+q,正反应为放热反应D.开始时充入C、D, m+n<p+q,正反应为吸热反应例6.可逆反应mAg+nBg eCg+fDg,当其它条件不变时,C 的体积分数φ与温度T、压强P的关系如图1和如图2所示,c下列说法正确的是A.达平衡后使用催化剂,C的体积分数变大B.达平衡后升温,平衡左移C.方程式系数m+n>e+fD.达平衡后增加A的量有利于平衡向正反应方向移动。

高考化学冲刺，等效平衡知识总结
一、概念
在一定条件下(恒温恒容或恒温恒压)，对同一可逆反应体系，起始时加入物质的物质的量不同，而达到化学平衡时，同种物质的百分含量相同，这样的平衡称为等效平衡。

二、等效平衡分类及规律
三、等效平衡判断四步曲
第一步：观察可逆反应特点(物质状态、气体分子数)，判断反应是反应前后气体体积不变的可逆反应还是反应前后气体体积改变的可逆反应；
第二步：挖掘反应条件，是恒温恒容还是恒温恒压，注意密闭容器不等于恒容容器；
第三步：采用一边倒法，将起始物质按可逆反应化学计量数之比转化成同一边的物质；
第四步：联系等效平衡判断依据，结合题目条件判断是否达到等效平衡。

1。

（1） （2）（3）2源自40 12a
0.5a
0
m
0.5
n(n≥2m) 2(n-2m)
(n-m)a
第三课时
等效平衡
条件 等效条件 结果
两次平衡时各组分百 分量、n、c均相同 两次平衡时各组分 百分量相同，n、c 同比例变化 两次平衡时各组分 百分量、c相同，n 同比例变化 投料换算成 恒温恒容 相同物质表 (△n(g)≠0) 示时量相同 投料换算成 恒温恒容 相同物质表 (△n(g)=0) 示时等比例 恒温恒压 投料换算成 相同物质表 示时等比例
4
练习：1、某温度下，向某密闭容器中加入 1molN2和3molH2,使之反应合成NH3，平衡 后测得NH3的体积分数为m。若T不变，只 改变起始加入量，使之反应平衡后NH3的 体积分数仍为m，若N2、H2、NH3的加入量 用X、Y、Z表示应满足： （1）恒定T、V： 2mol ①若X=0，Y=0，则Z= 2.25mol Z= 0.5mol ②若X=0.75，Y= ③X、Y、Z应满足的一般条件是
（2）对于反应前后气体分子数不变的可逆 反应 判断方法：极限转化法 只要反应物（或生成物）的物质的 量的比与原平衡相等，则二平衡等 效。 特点： 两次平衡时各组分百分量相同， 但n、c同比例变化
T、V不变
2SO2+O2
SO2 0mol O2 0mol SO3 2mol
2 SO3
SO2 1mol O2 0.5mol SO3 1mol SO2 0.5mol O2 0.25mol SO3 1.5mol
X+Z/2=1 ，Y+3Z/2=3 Y=3X，X+Y+2Z=4
（2）恒定T、P： ①若X=0、Y=0，则Z >0 ②若X=0.75,则Y=2.25mol Z ≥0 ③X、Y、Z应满足的一般条件是

16、业余生活要有意义，不要越轨。——华盛顿 17、一个人即使已登上顶峰，也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 19、自己活着，就是为了使别人过得更美好。——雷锋 20、要掌握书，莫被书掌握；要为生而读，莫为读而生。——布尔沃
END
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像高中化学等效平衡知识点总结 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮 回里有你。

等效平衡问题小结───用回归“定值．．”法解等效平衡问题初探．．”法或“定比密闭容器中一个既定的可逆反应，在建立平衡的条件完全相同时，只要参加反应的物质的量符合一定的比例条件，无论采取何种途径，最终能达到相同的平衡状态，这就是等效平衡问题（即平衡点等价原理）。

等效平衡都与气体物质参与的可逆反应有关，解答这一问题首先要明确两点：1.可逆反应前后气体的物质的量（或体积）是否相等。

2.可逆反应达平衡的条件是‘恒温恒容’还是‘恒温恒压’，然后确定采取何种方法求解。

对于可逆反应：mA（g）+nB（g） pC（g）+qD（g）来说Ⅰ.若m+n≠p+q①恒温恒容（容器体积不变）时,只要将各初始态物质的量设定‘回归’至与题给已知条件分别对应相等，则可使反应达平衡时与题给已知平衡等效。

这一方法即为：“回归定值“法。

②恒温恒压（容器体积变化）时，只要将各初始态物质的量之比‘回归’至与题给已知条件物质的量之比相等，则可使反应达平衡时与题给平衡等效。

这一方法即为：“回归定比”法。

Ⅱ.若m+n=p+q无论是‘恒温恒容’还是‘恒温恒压’，只需用“回归定比”发来解即可。

举例说明该法的应用：例1：某温度下，向密闭容器中加入2molSO2和1molO2使之发生反应：2SO2（g）+O2（g） 2SO3（g），当反应达平衡时，测得SO3的浓度为：Wmol/L。

若温度不变，只改变初始时物质的加入量，反应重新达到平衡后，SO3的浓度仍为Wmol/L。

若SO2、O2、SO3的加入量分别用a、b、c来表示，则应满足：⑴恒温恒容时，当a=0，b=0，则C= ；a=0.5mol b= ，c= 。

此时，a、b、c应满足的关系是。

⑵恒温恒压时，a=0，b=0，则C= ；a=0.5molb= ，c= ，此时，a、b、c应满足的关系是。

解析：⑴恒温恒容时，应用“回归定值”法当a=0，b=0，则c=2mol（相当于从逆反应开始）；a=0.5mol，b=0.25mol，c=1.5mol（相当于已有1.5molSO2已转化为1.5molSO3，且消耗了0.75molO2）。

等效平衡原理及规律总结哎呀，咱们今天来聊聊那个老生常谈但又让人头疼的问题——等效平衡原理。

你瞅瞅，这不就是生活中的小窍门嘛，有时候解决问题就像找到了那把钥匙，咔嚓一声，难题全解决了！咱们得先搞清楚什么是等效平衡原理。

简单来说，就是通过调整系统的某些参数，使得系统在某种情况下达到一种平衡状态，这种状态和原系统的状态是相同的。

听起来是不是挺高级的？其实说白了，就是“换汤不换药”，用不同的方法达到同一个结果。

比如说，咱们平时做饭，想要做出一道好菜，就得知道火候怎么调。

如果火候太大，菜会糊；火候太小，菜又吃不熟。

这时候，咱们就可以试试“等效平衡”的方法，比如调一调锅盖，让热气不那么快散去；或者换个大点的锅，让火力更集中一些。

这样一来，既能保证菜熟透又不糊锅，岂不美哉？再比如咱们玩跷跷板，想让跷跷板保持平衡，就得想办法让它两边的重量相等。

要是一边太重了，另一边轻了，那跷跷板就会倾斜。

这时候，咱们就可以调整一下两边的石头，让它们的重量差不多，这样跷跷板就能稳稳当当了。

这就是等效平衡原理的一个实际应用。

那么，等效平衡原理在生活中还有哪些应用呢？我来给你数几个例子。

咱们做数学题的时候，有时候会遇到一个看似无解的问题，这时候就可以用等效平衡的原理，通过改变问题的条件，找到新的解决方法。

咱们在谈恋爱时，有时候会遇到矛盾和冲突，这时候也可以用等效平衡的原理，通过沟通和妥协，让双方的关系更加和谐稳定。

咱们在处理人际关系时，也要学会用等效平衡的原理，让自己的心态保持平衡，这样才能更好地应对各种挑战。

等效平衡原理就像是我们生活中的指南针，帮助我们在面对各种问题时能够找到正确的方向。

只要我们用心去体会，去实践，相信我们一定能够在生活中运用好这个原理，让自己的生活变得更加美好。

所以啊，别小看了等效平衡原理哦，它可是咱们生活中的一大利器呢！。

等效平衡原理及规律总结哎呀，今天咱们聊聊等效平衡原理及规律总结这个话题，咋听起来有点高大上呢？其实啊，这里面涉及到的东西还是挺有趣的。

就跟我们日常生活中做菜一样，讲究的是火候、调料和比例，只有把这三点把握好了，才能做出美味可口的佳肴。

同样地，等效平衡原理及规律总结也是这样一门学问，它告诉我们如何在化学反应中保持平衡，从而让我们更好地理解这个世界。

咱们来聊聊什么是等效平衡。

简单来说，就是在一个封闭的系统里，各种物质之间的相互作用达到了一种稳定的状态。

这种状态就像我们生活中的平衡木一样，虽然摇摇晃晃，但总能保持在一条直线上。

那么，如何才能让这些物质保持平衡呢？这就需要用到等效平衡原理了。

等效平衡原理告诉我们，在化学反应中，只要各个物质的浓度不变，那么整个系统就会保持平衡。

这就像是我们在玩捉迷藏时，只要大家不被发现，游戏就能继续进行下去。

这并不是说只要浓度不变就万事大吉了。

我们还需要关注反应物和生成物之间的转化率，以及反应速率等因素。

只有这些因素都考虑到了，我们才能真正掌握等效平衡原理。

接下来，咱们来聊聊等效平衡规律。

在化学反应中，有些物质的浓度变化比较快，而有些物质的变化速度相对较慢。

这就像是我们生活中的“急性子”和“慢性子”一样，有些人做事雷厉风行，有些人则拖拖拉拉。

在等效平衡中，我们需要关注的是如何调整各个物质的浓度，以便让整个系统尽快达到平衡。

这个过程就像是我们在做饭时，需要不断地加入调料、翻炒和加水。

只有这样，才能让菜肴的味道更加丰富多彩。

同样地，在等效平衡中，我们需要不断地调整反应物和生成物的浓度，以及反应条件，以便让整个化学反应尽快达到平衡。

那么，如何才能更好地掌握等效平衡原理及规律呢？这就需要我们多做实验、多观察、多思考。

就像是我们在学习一门新技能时，需要不断地练习、摸索和总结经验一样。

只有这样，我们才能真正掌握这门学问，成为化学界的大咖。

当然啦，等效平衡原理及规律总结不仅仅是一门科学知识，它还可以应用到我们的日常生活中。

《化学平衡》复习小专题二等效平衡学习目标：1、理解什么是等效平衡、等效平衡的条件；2、会解决等效平衡的各类问题。

重点：等效平衡的应用；难点：等效平衡的理解。

一、等效平衡的条件小结：什么叫“等效平衡”？在一定条件下，同一可逆反应体系，不管从正反应开始，还是从逆反应开始，达到平衡时，任何相同物质的含量(体积分数、物质的量分数)都相同的化学平衡互称等效平衡。

可分为“全等效”平衡和“相似等效”平衡。

在一定条件下(恒温恒容或恒温恒压)，对同一可逆反应，起始时加入物质的二、等效平衡应用举例：2molA和1molB，发生反应2A(g)＋B(g) 2C(g)，达到平衡时，C的物质的量浓度为K mol/L，若维持容器体积和温度不变，按下列配比作为起始物质，A．4 molA+2 molB B．2 molA+1 molB+2 molC C．2 molC+1 molB D．2 molC E．1 molA+0.5 molB+1 molC①达到平衡后，C的物质的量浓度仍是K mol/L的是②A项平衡时，c(C)与2K mol/L的关系？③平衡时各选项中E的平衡浓度c(C)的大小顺序。

④若令a、b、c分别代表初始加入的A、B、C的物质的量，如果a、b、c取不同的数值，它们必须满足一定的相互关系，才能保证达到平衡时，反应混合物中三种气体的百分含量仍跟上述平衡时完全相同，填写：Ⅰ若a＝0，b＝0，则c＝___ _。

Ⅱ若a＝0.5，则b__ _，c＝__ __。

Ⅲa、b、c的取值必须满足的一般条件是（用两个方程式表示，一个只含a、c，另一个只含b、c）：__ __；。

1molN2和4molH2,使之反应合成NH3，平衡后测得NH3的体积分数为m。

若T不变，只改变起始加入量，使之反应平衡后NH3的体积分数仍为m，若N2、H2、NH3的加入量用X、Y、Z表示应满足：（1）恒定T、V：[1]若X=0，Y=0，则Z是否有恰当的取值?[2]若X=0.75，Y= ，Z= 。

专题六等效平衡【专题总结】一、等效平衡的概念1．定义：对于同一可逆反应，当外界条件一定时，无论该反应是从正反应开始，还是从逆反应开始，或是从中间状态（既有反应物又有生成物的状态）开始，只要到达平衡时反应混合物中各组分的分数（质量分数、物质的量分数或体积分数）对应相等就可达到相同的平衡状态，这就称为等效平衡。

2．标志：由以上定义我们可以看出，判断同一可逆反应达到的平衡状态是否达为等效平衡的标志是：达到平衡后，反应混合物中各组分的分数（质量分数、物质的量分数或体积分数）是否对应相等。

3．意义：等效平衡的概念的提出反映了化学平衡状态的建立与途径无关。

二、等效平衡的类型根据外界条件不同，等效平衡可以分为两大类：1、恒温恒容条件下的等效平衡在恒温、恒容的情况下，对于同一可逆反应，不论各反应物的起始量是多少，也不管反应物是一次加入或分几次加入，或是加入后分一次取出或分几次取出，只要各物质的起始量（质量、物质的量、浓度、体积等）按化学计量数换算成方程式左右两边同一边后对应相同，则就可以达到等效平衡。

这种情况下建立的等效平衡，不但平衡混合物中各组分的质量分数（物质的量分数、体积分数）对应相等，而且各组分的质量、体积、物质的量、浓度等也分别对应相等。

【典例解析】例1：在一个固定体积的密闭容器中，加入2molA和1molB发生以下反应：2A(g)+B(g) 3C(g)+D(g)，达到平衡时C的浓度为W moll/L。

若维护容器体积和温度不变，按下列四种配比作为起始物质，达到平衡时，D的浓度也为W/3 moll/L的是（）A．3molC+1molD B．2molA+2mol CC．2molA+1moB+0.5molD D．1molA+0.5molB+1.5molC+0.5molD解析：本题建立的两个平衡是恒温恒容下的等效平衡，需要各物质的起始量相等。

使用极端转化法，将把生成物全部推算成反应物或把反应物全部推算成生成物后，进行比较即可。