与或非逻辑关系的定义
- 格式:doc
- 大小:12.78 KB
- 文档页数:2


基本逻辑关系通常,把反映“条件”和“结果”之间的关系称为逻辑关系。
如果以电路的输入信号反映“条件”,以输出信号反映“结果",此时电路输入、输出之间也就存在确定的逻辑关系.数字电路就是实现特定逻辑关系的电路,因此,又称为逻辑电路.逻辑电路的基本单元是逻辑门,它们反映了基本的逻辑关系。
基本逻辑关系和逻辑门基本逻辑关系和逻辑门逻辑电路中用到的基本逻辑关系有与逻辑、或逻辑和非逻辑,相应的逻辑门为与门、或门及非门。
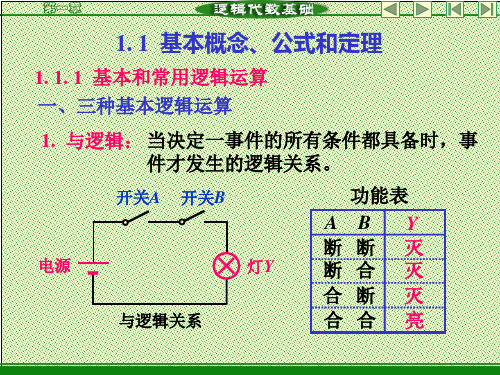
一、与逻辑及与门与逻辑指的是:只有当决定某一事件的全部条件都具备之后,该事件才发生,否则就不发生的一种因果关系。
如图2.1.1所示电路,只有当开关A 与B 全部闭合时,灯泡Y 才亮;若开关A 或B 其中有一个不闭合,灯泡Y就不亮.这种因果关系就是与逻辑关系,可表示为Y =A •B ,读作“A 与B”。
在逻辑运算中,与逻辑称为逻辑乘。
与门是指能够实现与逻辑关系的门电路。
与门具有两个或多个输入端,一个输出端。
其逻辑符号如图2。
1。
2所示,为简便计,输入端只用A 和B 两个变量来表示。
与门的输出和输入之间的逻辑关系用逻辑表达式表示为: Y =A •B =AB两输入端与门的真值表如表2.1.1所示。
波形图如图2。
1。
3所示。
A B Y0 0 0 0 1 0 1 0 0 1 11(a)常用符号表2.1.1 与门真值表 图2.1.1 与逻辑举例(b )国标符号图2.1.2 与逻辑符号图2.1.3 与门的波形图由此可见,与门的逻辑功能是,输入全部为高电平时,输出才是高电平,否则为低电平。
二、或逻辑及或门或逻辑指的是:在决定某事件的诸条件中,只要有一个或一个以上的条件具备,该事件就会发生;当所有条件都不具备时,该事件才不发生的一种因果关系。
如图2。
1。
4所示电路,只要开关A或B其中任一个闭合,灯泡Y就亮;A、B都不闭合,灯泡Y才不亮。
这种因果关系就是或逻辑关系。
可表示为:Y=A+B读作“A或B”。
在逻辑运算中或逻辑称为逻辑加。


基本逻辑函数及运算规律(与或非)基本的逻辑关系有与逻辑、或逻辑、非逻辑,与之对应的逻辑运算为与运算(逻辑乘)、或运算(逻辑加)、非运算(逻辑非)。
1.与运算只有当决定一件事情的条件全部具备之后,这件事情才会发生。
把这种因果关系称为与逻辑,其逻辑关系、真值表及逻辑符号如图6.7所示。
若用逻辑表达式来描述,则可写为:B A Y ⋅=(a)电路 (b)真值表 (c)逻辑符号图6.7 与运算下图6.8为实现与运算的二极管与门电路。
A 、B 为输入端,F 为输出端。
A 、B 输入端中只要有一个为低电平,则与该输入端相连的二极管会反相偏置导通,使输出端为低电平。
只有输入端同时为高电平时,二极管会反向偏置截止,输出才是高电平。
图 6.8 与运算的二极管与门电路2.或运算当决定一件事情的几个条件中,只要有一个或一个以上条件具备,这件事情就发生。
把这种因果关系称为或逻辑,其逻辑关系、真值表及逻辑符号如图6.9所示。
若用逻辑表达式来描述,则可写为:B A Y +=(a)电路 (b)真值表 (c)逻辑符号图6.9 或运算下图6.10为实现与运算的二极管或门电路。
A、B为输入端,F为输出端。
A、B输入端中只要有一个为高电平,则输出端为高电平。
只有当A、B同时为低电平,输出端才会输出低电平。
图 6.10或运算的二极管与门电路3.非运算某事情发生与否,仅取决于一个条件,而且是对该条件的否定,即条件具备时事情不发生;条件不具备时事情才发生,其逻辑关系、真值表及逻辑符号如图6.11所示。
(a)电路(b)真值表(c)逻辑符号图6.11 或运算Y若用逻辑表达式来描述,则可写为:A下图6.12为晶体管非门电路。
当输入为高电平,晶体管饱和,输出为低电平;当输入为电平,晶体管截止,输出为高电平,实现了非门功能。
图 6.12 非运算的二极管与门电路二、常用逻辑运算1.与非运算下图6.13为2输入与非运算的电路、逻辑符号及真值表。
它由二极管与门和晶体管非门串接而成,当输入中至少有一个为低电平,P点输出为低电平,晶体管截止,F输出为高电平;当输入全为高电平时,P点输出为高电平,晶体管饱和,F输出为低电平,实现了与非的逻辑功能。

与或非异或运算的逻辑表达式1.引言1.1 概述逻辑运算是计算机科学中非常重要的一部分,它在描述和处理真值(True/False)以及逻辑关系时起着至关重要的作用。
在逻辑运算中,与(AND)、或(OR)、非(NOT)以及异或(XOR)是我们经常会使用的四种基本逻辑运算。
与运算是指当且仅当所有的输入条件都为真时,结果才为真。
它的逻辑表达式可以用逻辑符号“∧”表示,例如,表达式“A∧B”代表A和B 都为真时,结果为真。
与运算除了在逻辑中常用外,在计算机科学中也广泛应用,例如在编程语言中,我们常常使用与运算来判断两个条件是否同时满足。
或运算是指当且仅当至少有一个输入条件为真时,结果才为真。
它的逻辑表达式可以用逻辑符号“∨”表示,例如,表达式“A∨B”代表A或者B其中一个为真时,结果为真。
或运算在逻辑中的一个重要应用是进行多个条件的判断,只要其中一个条件成立,我们就可以进行相应的操作。
非运算是指将输入条件取反,即如果原始条件为真,则取反后为假;如果原始条件为假,则取反后为真。
它的逻辑表达式可以用逻辑符号“¬”表示,例如,表达式“¬A”代表A的逆否命题。
非运算常常用于取反判断、条件判断等场景中,是逻辑推理中的一种重要手段。
异或运算是指当且仅当两个输入条件不同时,结果才为真。
它的逻辑表达式可以用逻辑符号“⊕”表示,例如,表达式“A⊕B”代表A和B不同时,结果为真。
异或运算在计算机领域特别常用,经常应用于数据的加密与解密、错误检测等方面。
本文将详细探讨与、或、非以及异或运算的定义、特点和逻辑表达式,并对它们的真值表进行分析。
同时,我们还将讨论逻辑运算在实际应用中的一些例子,帮助读者更好地理解逻辑运算的重要性和应用场景。
在深入理解这些逻辑运算的基础上,我们可以更准确地进行问题的分析和解决。
文章结构部分的内容如下:1.2 文章结构本文主要围绕与运算、或运算、非运算和异或运算的逻辑表达式展开讨论。
与或非逻辑关系的定义逻辑是一种研究思维和推理的学科,它主要关注的是判断和推理的正确性。
逻辑关系是指在一组命题之间所存在的某种关系,其中包括“与”、“或”、“非”等关系。
这些逻辑关系在数学、计算机科学、哲学等领域都有广泛的应用,因此我们有必要对它们进行深入的探究和了解。
一、与逻辑“与”逻辑是指两个或多个命题同时为真时,整个命题才为真。
例如,“今天是星期五”与“今天是6月份”两个命题只有同时成立才能构成真命题。
在逻辑符号中,“与”通常用“∧”表示。
与逻辑在数学中有着广泛的应用,例如在代数学中,我们常常用“与”逻辑来表示两个数之间的关系。
例如,如果我们要表示“x大于5且小于10”的命题,可以写成5<x<10,其中“<”符号表示与逻辑。
在计算机科学中,“与”逻辑也有着广泛的应用。
例如,在编写程序时,我们可以使用“与”逻辑来表示两个或多个条件同时满足时,程序才能执行某些操作。
二、或逻辑“或”逻辑是指两个或多个命题中只要有一个为真,整个命题就为真。
例如,“今天是星期五”或“今天是6月份”两个命题只要有一个成立就可以构成真命题。
在逻辑符号中,“或”通常用“∨”表示。
在数学中,“或”逻辑也有着广泛的应用。
例如,在代数学中,我们可以用“或”逻辑来表示两个数之间的关系。
例如,如果我们要表示“x小于5或大于10”的命题,可以写成x<5或x>10,其中“或”符号表示或逻辑。
在计算机科学中,“或”逻辑也有着广泛的应用。
例如,在编写程序时,我们可以使用“或”逻辑来表示两个或多个条件中只要有一个满足,程序就可以执行某些操作。
三、非逻辑“非”逻辑是指一个命题的否定。
例如,“今天不是星期五”这个命题的否定就是“今天是星期五”。
在逻辑符号中,“非”通常用“”表示。
在计算机科学中,“非”逻辑也有着广泛的应用。
例如,在编写程序时,我们可以使用“非”逻辑来表示某个条件不成立时,程序可以执行某些操作。
总结逻辑关系是一种描述命题之间关系的方法,包括“与”、“或”、“非”等关系。
布尔逻辑检索是信息检索领域中常用的一种检索方法,它通过布尔运算符(与、或、非)结合检索词语来实现信息的精确检索。
在布尔逻辑检索中,存在着三种重要的关系,分别是“与”、“或”、“非”的关系。
下面将对这三种关系进行详细阐述。
一、“与”的关系1.概念:布尔逻辑检索中的“与”关系,即表示检索结果中需要同时包含多个检索词汇的情况。
当用户输入“计算机”与“技术”两个检索词汇时,要求检索结果中的文档同时包含“计算机”和“技术”两个词汇。
2.特点:与关系的特点是要求检索结果的文档必须同时包含所有的检索词汇,这样可以有效提高检索的精确度和准确性,确保检索结果的相关性。
3.应用场景:与关系常用于需要精确匹配多个关键词的信息检索,例如专业领域的学术论文检索、法律案例检索等。
二、“或”的关系1.概念:布尔逻辑检索中的“或”关系,表示检索结果中包含任意一个或多个检索词汇的情况。
当用户输入“计算机”或“技术”两个检索词汇时,检索结果中的文档可以包含“计算机”或“技术”其中之一或两者皆有。
2.特点:或关系的特点是宽松度较大,能够容忍检索结果中存在多个可能相关的词汇,适合对信息的广泛查找和扩展搜索。
3.应用场景:或关系常用于需要扩展搜索范围和获取相关信息的情况,例如广告行业的关键词广告投放、市场调研报告检索等。
三、“非”的关系1.概念:布尔逻辑检索中的“非”关系,表示检索结果中不能包含某个检索词汇的情况。
当用户输入“计算机”非“技术”时,要求检索结果中的文档不能包含“技术”这个词汇。
2.特点:非关系的特点是排除性强,能够帮助用户排除一些干扰或无关的检索结果,提高检索效率和精确性。
3.应用场景:非关系常用于排除一些干扰因素或无关信息的情况,例如特定行业的竞争对手调查、新闻舆情监测等。
布尔逻辑检索的三种关系——“与”、“或”、“非”,分别适用于不同的信息检索需求。
合理运用这些关系,能够有效提高信息检索的精确性和准确性,满足用户在特定情境下的信息获取需求。
与或非逻辑关系的定义
逻辑学是一门研究思维和推理规律的学科,而逻辑关系则是逻辑学中的一个重要概念。
逻辑关系是指命题之间的关系,包括与、或、非三种关系。
在逻辑学中,这三种关系被称为“逻辑联结词”,它们分别表示命题之间的不同关系。
本文将详细介绍与、或、非三种逻辑关系的定义及其应用。
一、与逻辑关系的定义
与逻辑关系是指两个命题同时成立的关系。
用符号表示为“∧”,称为“逻辑与”,也称为“合取”。
例如,命题“今天是星期二”与命题“今天是晴天”可以表示为:“今天是星期二∧今天是晴天”。
这个命题的真值只有在两个命题同时成立时才为真。
与逻辑关系常用于描述两个或多个条件同时满足的情况。
例如,“如果今天是星期天且天气晴朗,我就去爬山。
”这个命题中,“今天是星期天”和“天气晴朗”是两个条件,只有同时满足才会去爬山。
二、或逻辑关系的定义
或逻辑关系是指两个命题中至少一个成立的关系。
用符号表示为“∨”,称为“逻辑或”,也称为“析取”。
例如,命题“今天是星期二”或命题“今天是晴天”可以表示为:“今天是星期二∨今天是晴天”。
这个命题的真值只有在两个命题中至少一个成立时才为真。
或逻辑关系常用于描述两个或多个条件中只要有一个满足就可
以的情况。
例如,“如果今天是星期天或天气晴朗,我就去游泳。
”这个命题中,“今天是星期天”和“天气晴朗”是两个条件,只要满足
其中一个就会去游泳。
三、非逻辑关系的定义
非逻辑关系是指命题的否定关系。
用符号表示为“”,称为“逻
辑非”。
例如,命题“今天是星期二”可以表示为:“今天不是星期二”。
这个命题的真值只有在今天不是星期二时才为真。
非逻辑关系常用于否定一个命题,或者表示一个条件不成立的情况。
例如,“如果今天不下雨,我就去跑步。
”这个命题中,“今天不
下雨”是一个条件,表示只有在今天不下雨的情况下才会去跑步。
四、逻辑关系的应用
逻辑关系在日常生活中应用广泛,尤其在科学、数学和哲学等领域中应用更为广泛。
逻辑关系可以帮助我们更准确地表达和理解命题,从而更好地进行推理和判断。
例如,在数学中,逻辑关系可以帮助我们更好地理解集合和命题之间的关系。
在计算机科学中,逻辑关系可以帮助我们设计和实现逻辑电路和程序。
在哲学中,逻辑关系可以帮助我们更好地理解和分析论证过程。
总之,逻辑关系是逻辑学中的一个重要概念,包括与、或、非三种关系。
这三种关系可以帮助我们更准确地表达和理解命题,从而更好地进行推理和判断。
在日常生活和学术研究中,逻辑关系都有着广泛的应用。