2014四年级希望杯100题答案4
- 格式:pdf
- 大小:1.72 MB
- 文档页数:9

第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。

希望杯四年级试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的?A. 2+3=5B. 3+4=7C. 5+5=10D. 4+5=9答案:C2. 哪个图形是正方形?A. □B. ○C. △D. ▢答案:A3. 以下哪个单词拼写正确?A. colerB. colerfulC. colerfullD. colorful答案:D4. 下列哪个是正确的分数?A. 1/2B. 2/1C. 3/1D. 4/2答案:A5. 哪个数字是最小的?A. 3B. 2C. 1D. 0答案:D6. 下列哪个选项是正确的?A. 4-2=1B. 5-3=2C. 6-4=3D. 7-5=4答案:B7. 哪个是正确的乘法?A. 2×3=6B. 3×4=10C. 4×5=15D. 5×6=30答案:A8. 哪个是正确的除法?A. 8÷2=3B. 9÷3=2C. 10÷4=2D. 12÷6=1答案:B9. 下列哪个是正确的时间?A. 12:00 PMB. 12:00 AMC. 6:00 PMD. 6:00 AM答案:A10. 哪个是正确的月份?A. 一月B. 二月C. 三月D. 四月答案:B二、填空题(每题4分,共20分)1. 一个长方形的长是6厘米,宽是4厘米,它的面积是______平方厘米。
答案:242. 一个数的3倍是9,这个数是______。
答案:33. 一个数加上5等于10,这个数是______。
答案:54. 一个数减去2等于3,这个数是______。
答案:55. 一个数乘以2等于8,这个数是______。
答案:4三、解答题(每题5分,共20分)1. 一个苹果比一个梨重200克,如果一个苹果重500克,那么一个梨重多少克?答案:一个梨重300克。
2. 小明有10个苹果,他给了小红3个,然后又买了5个,小明现在有多少个苹果?答案:小明现在有12个苹果。

2014年四年级希望杯100题1、计算:67+135-5×7+264÷82、计算:13+29+32+46+57+68+71+85+943、计算:364×25÷(14÷4 )4、计算:(1953+1956+1958+1962+1959+1947+1957 )÷75、将运算符号“+ ,- , × , ÷”填在下面的圆圈中,使得算式成立. 2○2○2○2○2=56、在四个数:10、10、4、4之间填入“+”、“-”、“×”、“÷”“()”,使写出的算式的计算结果是24。
7、两个自然数的和是94,积是2013 ,求这两个数。
8、按顺序排列的7个数,它们的平均数是9 ,已知前4个数的平均数是5 ,后4个数的平均数是12,求第四个数。
9、若5个连续自然数的和是1265,求这5个自然数中最小的数。
10、20至24这5个连续自然数的和再加上2000等于另外4个连续自然数的和,求另外4 个连续自然数中最小的数。
11、有3个数a、b、c ,要求计算a- ( b+c ),李辉算成了 a-b+c,结果多出100,求c12、一个两位数,在它的两个数字中间添加一个0,就比原来的数多720 ,这样的两位数最大是多少?.13、四位数6823的a倍是各位数字不同的最小的六位数,求a.=⨯,求 d.14、六位数aabccd满足:aabccd ddd ddd15、某手机号码是abcbdeefcgh ,已知其中不同的字母代表1, 2, 3,…,9中的不同的数字,d 最大,h比d小2 ,而且a<e<b<c<f<g<h ,请写出这个手机的号码.16、将1,2,3,4,5,6分别写到一个正方体的六个面内,将相对两个面内的数作为一个长方形的长和宽,计算这样得到的长方形的面积的和,求和的最大值,最小值.17、用21跟小棒摆成10个三角形,如图按照这种方式,用65根小棒能摆出多少个三角形?18、观察下面算式的规律,求第100个算式的得数.2+3, 3+7, 4+11, 5+15,…19、爷爷今年60岁,三个孙子的年龄分别是12岁、10岁和8岁,那么,几年后三个孙子的年龄和等于爷爷的年龄?20、小红长到妈妈今年的年龄时,妈妈77岁。

第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
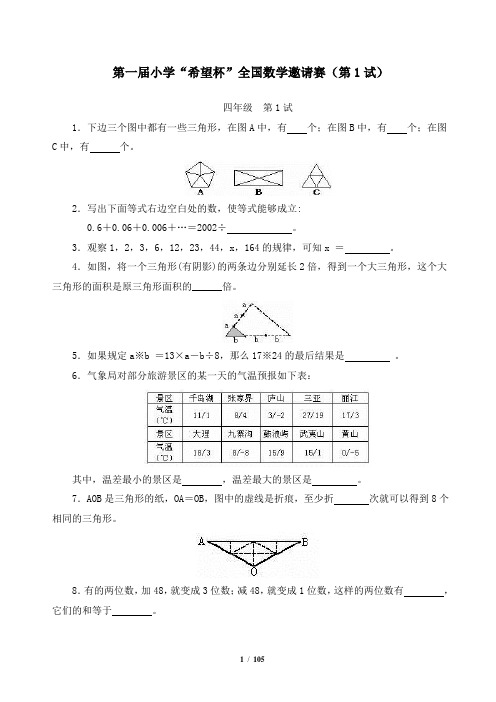
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
2012第10届希望杯四年级培训题100题1、已知:(1+1+1)×37=111;(2+2+2)×37=222;(3+3+3)×37=333;则24×37= 。
2、一个除法算式中,被除数是173,除数是自然数,且与商相等,则余数、除数、商的和是。
3、定义运算“▽”和“△” :当a ≥ b 时,a ▽b = b ▽a = b ,a △b = b △a = b 。
若非零自然数m 满足:5△[7▽(m △4)]=6,则m = 。
4、已知三个自然数的乘积是奇数,如果将其中两个数各减去1 后,这三个数的乘积是416,那么原来三个数的乘积是。
5、算式1×3×5×7×9×11 的结果的末位数字是。
6、如果6 个连续奇数的乘积是135135,那么这6 个数的和是。
7、若图中每个小方格的面积都是1,则阴影四边形ABCD 的面积是。
8、若5个3相乘得a ,2011个5 连乘得b,2012个2连乘得c,则a × b × c的结果是位数。
9、28 位小朋友排成一行,从左向右数,第10 位是张华,张华左边的左边是李明,那么从右向左数,李明是第位。
10、将连续自然数1、2、3、4、5、6、7、…逐个相加,得结果2012.验算时发现,漏加了一个数,那么这个漏加的数是。
11、桌子上有一些红豆和绿豆,绿豆的颗数是红豆颗数的11倍,后来绿豆开始长相思,结果45颗变成了红豆,这时候红豆与绿豆一样多,那么原来有红豆颗。
12、将120 名男生和140 名女生分成若干小组,要求每组男生的人数相同,女生的人数也相同,则最多可以分成组。
13、若2011=□4□□-□□17,则满足要求的算式有个。
14、有1、2、3、4、5、6、7、8、9 这九个数字组成如图2 所示的算式(每个数字仅出现一次)已给出四个数字,请在方框中填入合适数字。
15、一张正方形的纸板,长是70 厘米,剪下一个最大的正方形,余下一个小长方形纸板,用这个小长方形纸板做一个相框,则相框的周长是厘米。
第16届希望杯考前训练100题学前知识点梳理主要针对“希望杯”全国数学邀请赛进行考前特训,主要学习内容有:1.整数的四则运算,运算定律,简便运算。
2.基本图形,图形的拼组(分、合、移、补),图形的变换,折叠与展开。
3.角的概念与度量,长方形、正方形的周长和面积,平行四边形、梯形的概念和周长计算。
4.整除概念,数的整除特征,带余数除法,平均数。
5.几何计数(数图形),找规律,归纳,统计,可能性。
6.数谜,分析推理能力,数位,十进制表示法。
7.生活数学(钟表,时间,人民币,位置与方向,长度,质量的单位)。
8.应用题(植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题)。
考前100题选讲1.计算:8×27×25。
2.计算:9+98+987+9876。
3.计算:2-4+6-8+10-12+…-48+50。
4.计算:2017×2016+2016×2014-2015×2016-2015X2017。
第 1 页共 32 页5.计算:15÷7+68÷14。
6.已知999999÷(a÷2)=142857,求a7.某数被27除,商是8,余数是5,求这个数。
8.定义:A*B=(A+3)×(B-2),求15*17。
9.除法算式△÷7=12……□中,余数最大是多少?10.有5个连续偶数之和恰好等于4个连续奇数之和,如4+6+8+10+12=7+9+11+13。
请写出一个符合要求的式子。
11.将36表示成三个大于1的自然数的乘积(不考虑三个自然数的相乘顺序)。
共有几种不同的表示方法?12.用数字2,0,1,7可以组成多少个不重复的三位数?13.用2295除以一个两位数,丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了,得到的结果是45,则正确的结果应该是多少?14.如果把某个除法算式的被除数152写成125,则商会比原来的结果小3,且余数不发生变化,求余数?15.2017和某个小于100的自然数的和正好等于两个连续自然数之积,求这个小于100的自然数。
目录1.第一届小学“希望杯”全国数学邀请赛(第1试) (2)2. 第一届小学“希望杯”全国数学邀请赛(第2试) (5)3. 第二届小学“希望杯”全国数学邀请赛(第1试) (7)4. 第二届小学“希望杯”全国数学邀请赛(第2试) (10)5. 第三届小学“希望杯”全国数学邀请赛(第1试) (13)6. 第三届小学“希望杯”全国数学邀请赛(第2试) (16)7. 第四届小学“希望杯”全国数学邀请赛(第1试) (18)8. 第四届小学“希望杯”全国数学邀请赛(第2试) (21)9. 第五届小学“希望杯”全国数学邀请赛(第1试) (23)10. 第五届小学“希望杯”全国数学邀请赛(第2试) (26)11. 第六届小学“希望杯”全国数学邀请赛(第1试) (28)12. 第六届小学“希望杯”全国数学邀请赛(第2试) (30)13. 第七届小学“希望杯”全国数学邀请赛(第1试) (32)14. 第七届小学“希望杯”全国数学邀请赛(第2试) (36)15. 第八届小学“希望杯”全国数学邀请赛(第1试) (39)16. 第八届小学“希望杯”全国数学邀请赛(第2试) (41)17. 第九届小学“希望杯”全国数学邀请赛(第1试) (44)18. 第九届小学“希望杯”全国数学邀请赛(第2试) (46)19. 第十届小学“希望杯”全国数学邀请赛(第1试) (48)20. 第十届小学“希望杯”全国数学邀请赛(第2试) (50)21.第一届---第八届“希望杯”全国数学邀请赛参考答案 (53)第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。