精品解析：【全国校级联考】西南名校联盟(云南师大附中)2018届高三适应性月考卷(4)理数试题(解析版)

云南师大附中2018届高考适应性月考卷（六）英语参考答案第一部分听力（共两节，满分30分）1~5 ABCCB 6~10 CBBCA 11~15 ABCAC 16~20 AABBC第二部分阅读理解（共两节，满分40分）第一节（共15小题；每小题2分，满分30分）21~25 CCDDB 26~30 DBBAA 31~35 CACAB第二节（共5小题；每小题2分，满分10分）36~40 DEGAF第三部分语言知识运用（共两节，满分45分）第一节（共20小题；每小题1.5分，满分30分）41~45 BACDB 46~50 DBADC 51~55 ADABC 56~60 ABCDC第二节（共10小题；每小题1.5分，满分15分）61．is given 62．itself 63．which 64．fifteenth 65．better/well 66．between 67．a 68．exception 69．to return 70．awake第四部分写作（共两节，满分35分）第一节短文改错（共10小题；每小题1分，满分10分）I’ll never forget the experience as a volunteer for an international marathon race．As one of the three volunteers selecting from our school，I felt excited．In our spare time I practiced a①selected ②mygreat deal of，especially in my spoken English to ensure the best service．Then comes the day．Early③④camein the morning I arrived there the match would begin and found many volunteers already there do⑤where ⑥doing preparations．During the match，I，with the others，were busy helping the runners all the time．We⑦waswere highly praised for which we did，without which，the race could∧have been a success．⑧what ⑨not或couldn’tIt was my first time to be a volunteer for such important a sport event，which made me proud．⑩so第二节书面表达（满分25分）【参考范文】Dear Tom，In your email you asked about tea in China．Let me tell you something．Tea has a long history in China，dating back to 5,000 years ago．Obviously it plays an important part in Chinese culture．A great many distinguished poets and writers have written many masterpieces in appreciation of tea and about the love for it，among whom was Lu Yu in the Dang Dynasty，who wrote Cha Jing，the first book on tea，and was regarded as the “Tea Saint”．Chinese people take delight in tea-drinking．It is served not only at a tea house or restaurant，but also at home or during breaks at offices．Whenever guests visit，offering a cup of tea to them is a basic social custom．Tea is part of the Chinese’s daily life．I hope you can come to China to learn more about it．Yours，Li Hua【解析】第二部分阅读理解第一节A【语篇导读】本文为应用文。

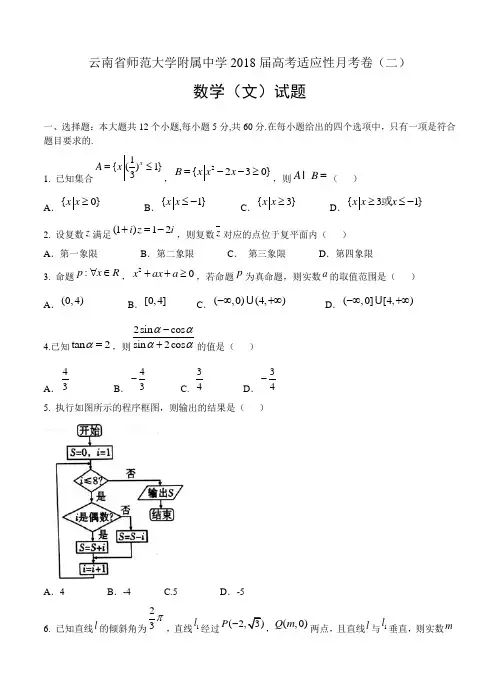
云南省师范大学附属中学2018届高考适应性月考卷（二）数学（文）试题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合1{()1}3xA x=≤，2{230}B x x x=--≥，则A B=I（）A．{0}x x≥B．{1}x x≤-C．{3}x x≥D．{31}x x x≥≤-或2. 设复数z满足(1)12i z i+=-，则复数z对应的点位于复平面内（）A．第一象限B．第二象限C．第三象限D．第四象限3. 命题:p x R∀∈，20x ax a++≥，若命题p为真命题，则实数a的取值范围是（）A．(0,4)B．[0,4]C．(,0)(4,)-∞+∞U D．(,0][4,)-∞+∞U4.已知tan2α=，则2sin cossin2cosαααα-+的值是（）A．43B．43-C.34D．34-5. 执行如图所示的程序框图，则输出的结果是（）A．4 B．-4 C.5 D．-56. 已知直线l的倾斜角为23π，直线1l经过(3)P-，(,0)Q m两点，且直线l与1l垂直，则实数m的值为（ ）A ．-2B ．-3 C. -4 D ．-5 7.已知等差数列{}n a 中，48a =，1348a a a a +++=（ ）A ．8B ．16 C. 24 D ．328.若实数,x y 满足不等式组2010220x x y x y -≤⎧⎪-+≥⎨⎪++≥⎩，则23z x y =+的最小值是（ ）A ．-11B ．-12 C. -13 D ．-149.已知某空间几何体的三视图如图所示，则该几何体的表面积是（ ）A ．122226+B ．12226+ C. 12226+ D ．122610.已知三棱锥P ABC -的所有顶点都在球O 的球面上，PA AB ⊥，PA AC ⊥，060BAC ∠=，2PA =，2AB =，3AC =，则球O 的表面积为（ ）A ．403πB ．303π C. 203π D ．103π11. 点P 在椭圆22221(0)x y a b a b +=>>上，12,F F 是椭圆的两个焦点，01260F PF ∠=，且12F PF ∆的三条边2||PF ，1||PF ，12||F F 成等差数列，则此椭圆的离心率是（ ）A ．45B ．34 C. 23 D ．1212.已知函数11()()2ln f x a x x x =--（a R ∈），()g x ax =-，若至少存在一个01[,1]x e ∈，使得00()()f xg x >成立，则实数a 的取值范围为（ ）A ．(1,)+∞B ．[1,)+∞ C. (0,)+∞ D ．[0,)+∞ 第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知向量(,2)a m =r ，(2,1)b =-r ，且()2a b b +⊥r r r，则m = ．14.已知双曲线22221x y a b -=(0,0)a b >>的焦点与抛物线216x ay =的焦点重合，则双曲线的离心率为 ．15.在ABC ∆中，3B π=，3AB =，2BC =，则cos A = ．16. 已知函数23,30()ln(1),03x x x f x x x ⎧-+-≤≤=⎨+<≤⎩，若()()33g x f x ax a =--有三个零点，则实数a 的取值范围是 ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 在ABC ∆中，,,a b c 分别是角,,A B C 的对边，(2)cos cos 0b c A a C --=. （1）求角A 的大小；（2）若2a =，求ABC ∆的面积S 的最大值.18. 为考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校高中生中，从男生中随机抽取了70人，从女生中随机抽取了50人，男生中喜欢数学课程的占47，女生中喜欢数学课程的占710，得到如下列联表. 喜欢数学课程 不喜欢数学课程 合计 男生 女生 合计（1）请将列联表补充完整；试判断能否有90%的把握认为喜欢数学课程与否与性别有关；（2）从不喜欢数学课程的学生中采用分层抽样的方法，随机抽取6人，现从6人中随机抽取2人，求抽取的学生中至少有1名是女生的概率..附：2 2()()()()()n ad bcka b c d a c b d-=++++，其中n a b c d=+++.2()P K k≥0.150 0.100 0.050 0.025 0.010 0.005 0.001 0k 2.072 2.706 3.841 5.024 6.635 7.879 10.828 19. 如图，四棱锥P ABCD-的底面ABCD是平行四边形，PA⊥底面ABCD，3PA=，2AD=，4AB=，060ABC∠=.（1）求证：平面PBC⊥平面PAC；（2）若点,M N分别为,PA CD上的点，且35PM CNPA CD==，在线段PB上是否存在一点E，使得//MN平面ACE；若存在，求出三棱锥P ACE-的体积；若不存在，请说明理由.20. 已知函数1()ln1f x a xx=++.（1）当1a=时，求函数()f x的单调区间和极值；（2）是否存在实数a，使得函数()f x在[1,]e上的最小值为1？若存在，求出a的值；若不存在，请说明理由.21. 已知点A为圆228x y+=上一动点，AN x⊥轴于点N，若动点Q满足(1)OQ mOA m ON=+-u u u r u u u r u u u r（其中m为非零常数）（1）求动点Q的轨迹方程；（2）当2m =时，得到动点Q 的轨迹为曲线C ，斜率为-1的直线l 与曲线C 相交于B ，D 两点，求OBD ∆面积的最大值.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程在平面直角坐标系xOy 中，已知直线l 经过点1(1,)2P ，倾斜角3πα=，在以原点O 为极点，x 轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ=（1）写出直线l 的参数方程，并把曲线C 的极坐标方程化为直角坐标方程； （2）设l 与曲线C 相交于,A B 两点，求PA PB•的值.23.选修4-5：不等式选讲 设函数()221f x x x =--+.（1）解不等式()0f x ≤；（2）若对于x R ∀∈，使2()24f x m m -≤恒成立，求实数m 的取值范围.云南师大附中2018届高考适应性月考卷（二） 文科数学参考答案一、选择题（本大题共12小题，每小题5分，共60分）1．{|0}{|31}A x x B x x x ==-≥，≥或≤，∴{|3}A B x x =I ≥，故选C ． 2．12i 13i 1i 22z -==--+，13i22z =-+，故选B ． 3．对于20x x ax a ∀∈++R ，≥成立是真命题，∴240a a ∆=-≤，即04a ≤≤，故选B ．4．∵tan 2α=，∴cos 0α≠，∴2sin cos 2tan 13sin 2cos tan 24αααααα--==++，故选C ． 5．由题意可知输出结果为123484S =-+-+-⋅⋅⋅+=，故选A ．6．∵11l l k k ==-g ，∴5m =-，故选D ．7．∵13248622a a a a a a +=+=，，又2642a a a +=，∴13482642()432a a a a a a a +++=+==，故选D ． 8．画出不等式组表示的可行域知，23z x y =+的最小值为14-，故选D ．9．由三视图知：几何体为四棱锥，且四棱锥的一条侧棱与底面垂直，如图，PA ⊥平面ABCD ，2PA =，2AB =，4AD =，2BC =，经计算，PD =，PC =，DC =，∴PC CD ⊥，∴12222PAB S =⨯⨯=△， 12442PAD S =⨯⨯=△，122PBC S =⨯⨯△，12PCD S =⨯=△，1(24)262ABCD S =⨯+⨯= ∴122226S =++表，故选A ．10．设ABC △外接圆半径为r ，三棱锥外接球半径为R ，∵2360AB AC BAC ==∠=︒，，，∴2222212cos602322372BC AB AC AB AC =+-︒=+-⨯⨯⨯=g g ，∴7BC 2sin60BCr ==︒ 72213，∴21r =，由题意知，PA ⊥平面ABC ，则将三棱锥补成三棱柱可得，22221101293PA R r ⎛⎫=+=+= ⎪⎝⎭，∴210404π4ππ33S R ==⨯=，故选A ．11．设1122||||PF r PF r ==，，由椭圆的定义得：122r r a +=，∵12F PF △的三条边2PF ||， 112||||PF F F ，成等差数列，∴1222r c r =+，联立122r r a +=，1222r c r =+，解得12224233a c a cr r +-==，，由余弦定理得：2221212(2)2cos60c r r r r =+-︒g ，将12224233a c a c r r +-==，代入2221212(2)2cos60c r r r r =+-︒g 可得，222243a c c +⎛⎫=+ ⎪⎝⎭ 2422242123332a c a c a c -+-⎛⎫- ⎪⎝⎭g g g ，整理得：2220c ac a +-=，由c e a =，得2210e e +-=，解得：12e =或1e =-（舍去），故选D ．12．若至少存在一个011e x ⎡⎤∈⎢⎥⎣⎦，，使得00()()f x g x >成立，则()()0f x g x ->在11e x ⎡⎤∈⎢⎥⎣⎦，有解，即112ln 2ln 0a a x ax x x x x ⎛⎫--+=+> ⎪⎝⎭在11e x ⎡⎤∈⎢⎥⎣⎦，上有解，即2ln a x x >-g 在11e x ⎡⎤∈⎢⎥⎣⎦，上至少有一个x成立，令()2lnh x x x=-g，()2(ln1)h x x'=-+，所以()h x在11e⎡⎤⎢⎥⎣⎦，上单调递减，则min()(1)0h x h==，因此0a>，故选C．13．(23)2(42)a b m b+=-=-r r r，，，，∵()2a b b+⊥r r r，∴(2)(4)320m-⨯-+⨯=，∴72m=．144a，∴2215ba=，∴双曲线的离心率4e==．15．在ABC△中，由余弦定理得2222212cos3223272AC AB BC AB BC B=+-=+-⨯⨯⨯=g g，∴AC=，由正弦定理得2sinsinBC BAAC==g，∵BC AC<，∴π3A B<=，∴cos A．16．由()|()|330g x f x ax a=--=，得|()|333(1)f x ax a a x=+=+，设3(1)y a x=+，则直线过定点(10)-，，作出函数|()|f x的图象（图象省略）．两函数图象有三个交点.当30a≤时，不满足条件；当30a>时，当直线3(1)y a x=+经过点(3ln4)，时，此时两函数图象有3个交点，此时ln434a=，ln26a=；当直线3(1)y a x=+与ln(1)y x=+相切时，有两个交点，此时函数的导数1()1f xx'=+，设切点坐标为()m n，，则ln(1)n m=+，切线的斜率为1()1f mm'=+，则切线方程为1ln(1)()1y m x mm-+=-+，即1ln(1)11my x mm m=-++++g，∵131am=+且3ln(1)1ma mm=-+++，∴1ln(1)11mmm m=-++++，即1ln(1)111mmm m+=+=++，则1em+=，即e1m=-，则1131eam==+，∴13ea=，∴要使两个函数图象有3个交点，则ln2163ea<≤．三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分） 解：（Ⅰ）因为(2)cos cos 0b c A a C --=，所以2cos cos cos 0b A c A a C --=，由正弦定理得2sin cos sin cos sin cos 0B A C A A C --=， 即2sin cos sin()0B A A C -+=，又πA C B +=-，所以sin()sin A C B +=， 所以sin (2cos 1)0B A -=，在ABC △中，sin 0B ≠，所以2cos 10A -=，所以π3A =．（Ⅱ）由余弦定理得：222222cos a b c bc A b c bc =+-=+-，∴42bc bc bc -=≥，∴1sin 42S bc A ===，当且仅当b c =时“=”成立，此时ABC △为等边三角形，∴ABC △的面积S 18．（本小题满分12分）由题意得22120(40153035) 2.05770507545K ⨯⨯-⨯=≈⨯⨯⨯，∵2.057 2.706<，∴没有90%的把握认为喜欢数学课程与否与性别有关．）（Ⅱ）用分层抽样的方法抽取时，抽取比例是624515=，则抽取男生230415⨯=人，抽取女生215215⨯=人． 记抽取的女生为AB ，，抽取的男生为a b c d ，，，， 从中随机抽取2名学生共有15种情况：()()()()()()()()()()()A B A a A b A c A d B a B b B c B d a b a c ，，，，，，，，，，，，，，，，，，，，，，()()()()a d b c b d c d ，，，，，，，．其中至少有1名是女生的事件为：()()()()()()()()()A B A a A b A c A d B a B b B c B d ，，，，，，，，，，，，，，，，，，有9种情况．记“抽取的学生中至少有1名是女生”为事件M ，则93()155P M ==．19．（本小题满分12分）（Ⅰ）证明：由已知，得AC ==，∵2BC AD ==，4AB =，又222BC AC AB +=，∴BC AC ⊥．又PA ⊥底面ABCD ，BC ⊂平面ABCD ，则PA BC ⊥， ∵PA ⊂平面PAC ，AC ⊂平面PAC ，且PA AC A =I ，∴BC ⊥平面PAC ．∵BC ⊂平面PBC ，∴平面PBC ⊥平面PAC ．（Ⅱ）线段PB 上存在一点E ，使得MN ∥平面ACE ．证明：在线段PB 上取一点E ，使35PE PB =，连接ME AE EC MN ，，，，∵35PM PE PA PB ==，∴ME AB ∥，且35ME AB =，又∵CN AB ∥，且35CN AB=，∴CN ME ∥，且CN ME =，∴四边形CEMN 是平行四边形，∴CE MN ∥，又CE ⊂平面ACE ，MN ⊄平面ACE ，∴MN ∥平面ACE ．∴3111325552P ACE E PAC B PAC PAC V V V S BC ---====⨯⨯⨯=g △． 20．（本小题满分12分）解：由题意知函数的定义域为{|0}x x >，()1a x af x x x -'=-+=． （Ⅰ）当1a =时，11()1x f x x x -'=-+=， 当01x <<时，()0f x '<，当1x >时，()0f x '>，所以函数()f x 的单调递减区间是(01)，，单调递增区间是(1)+∞，． 所以当1x =时，函数()f x 有极小值(1)ln1112f =++=，无极大值．（Ⅱ）①当1a ≤时，函数()f x 在[1e]，为增函数， ∴函数()f x 在[1e]，上的最小值为(1)ln1112f a =++=，显然21≠，故不满足条件； ②当1e a <≤时，函数()f x 在[1)a ，上为减函数，在[e]a ，上为增函数 故函数()f x 在[1e]，上的最小值为()f x 的极小值()ln 1=1f a a a a =-++， 即e a =，满足条件；③当e a >时，函数()f x 在[1e]，为减函数， 故函数()f x 在[1e]，上的最小值为1(e)ln e 11e f a =++=，即e a =，不满足条件．综上所述，存在实数e a =，使得函数()f x 在[1e]，上的最小值为1． 21．（本小题满分12分）解：（Ⅰ）设动点00()()Q x y A x y ，，，，则0(0)N x ，，且22008x y +=，① 又(1)OQ mOA m ON =+-u u u r u u u r u u u r ，得001x x y y m ==，，代入①得动点Q 的轨迹方程为222188x y m +=．（Ⅱ）当2m =时，动点Q 的轨迹曲线C 为22184x y +=．设直线l 的方程为y x b =-+，代入22184x y +=中，得2234280x bx b -+-=，由22(4)43(28)0b b ∆=--⨯⨯->，∴212b <， 设1122()()B x y D x y ，，，，2121242833b b x x x x -+==g ，，∵点O 到直线l 的距离d =||BD2211222OBD b b S d BD +-===g g △，当且仅当2212b b =-，即2612b =<时取到最大值．∴OBD △面积的最大值为22．（本小题满分10分）【选修4−4：坐标系与参数方程】解：（Ⅰ）直线l 的参数方程为：112()12x t t y ⎧=+⎪⎪⎨⎪=⎪⎩，为参数，，曲线C 的直角坐标方程为：2213x y +=．（Ⅱ）把直线l的参数方程11212x t y ⎧=+⎪⎪⎨⎪=+⎪⎩，，代入曲线C 的方程2213x y +=中，得221113322t ⎛⎫⎛⎫++= ⎪ ⎪ ⎪⎝⎭⎝⎭，即2104)50t t +-=， 设点A B ，所对应的参数分别为12t t ，，则1212t t =-g ， ∴121211||||||||||22PA PB t t t t ===-=g g g ．23．（本小题满分10分）【选修4−5：不等式选讲】解：（Ⅰ）不等式()0f x ≤，即|2||21|x x -+≤，即2244441x x x x -+++≤，23830x x +-≥，解得133x x -≥或≤， 所以不等式()0f x ≤的解集为133x x x ⎧⎫-⎨⎬⎩⎭≥或≤. （Ⅱ）1321()|2||21|312232x x f x x x x x x x ⎧+<-⎪⎪⎪=--+=-+-⎨⎪-->⎪⎪⎩，，，≤≤，，，故()f x 的最大值为1522f ⎛⎫-=⎪⎝⎭，因为对于x ∀∈R ，使2()24f x m m -≤恒成立， 所以25242m m +≥，即24850m m +-≥， 解得1522m m -≥或≤，∴5122m ⎛⎤⎡⎫∈-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭U ，，．。

云南师大附中2018届高考适应性月考卷（三）理科数学参考答案一、选择题（本大题共12小题，每小题5分，共60分）题号1 2 3 4 5 6 7 8 9 10 11 12 答案 B C B C A C C A D D D A【解析】1．22{|3}{|30}[33]B x yx x x ≥，，所以={101}A B ，，，故选B ．2．由题意知53i 22i 2i z，z 的共轭复数等于22i ，故选C ．3．q ：A B ，在同高处的截面积恒相等，p A B ：，的体积相等，故q 是p 的必要不充分条件，故选B ．4．5211x 的展开式的通项为51521C (1)0r rr r T r x ，，1，2，3，4，5．当因式2(3)x中提供2x 时，则取4r；当因式2(3)x 中提供3时，则取5r ，所以5221(3)1x x 的展开式的常数项是2，故选C ．5．双曲线22221(00)xy a b ab ，的渐近线方程为b y x a ，所以32b a ，双曲线的一个焦点在抛物线247y x 准线方程7x 上，所以7c ，由此可解得23a b ，，所以双曲线方程为22143xy ，故选A ．6．因为3131π()sin 2cos2sin 23sin 2cos23sin 222226f x x x x x x x ，所以π()23cos 26f x x ，故A 错误，当π2x 时，π5π2=66x ，故B 错误，对于D ，应向右平移π12个单位，故选C ．7．4n 时，31Q ，此时P Q ，则输入的a 的值可以为3，故选C ．8．设等比数列{}n a 的首项为1a ，公比为q ，依题意有：3242(2)a a a ，23428a a a得38a ，故31123120=8a qa q a a q ，，解之得122a q ，或13212a q ，，又{}n a 单调递减，所以663S ，故选A ．9．由题意知，球O 的半径5R ，直三棱柱111ABC A B C -的底面外接圆半径为4，则直三棱柱111ABC A B C -的高为6，则该三棱柱的体积为243，故选D ．10．由题意，2225233b c b A c b a B a a ，，，，，代入到椭圆方程整理得222225199c b a a ，联立22b a ，解得3a ，故选D ．11．17115()()()48228AE AF AB BE AD DF AB BC AD DC ≥，当且仅当122，即1时取等号，故选D ．12．22()3()30f x x f x x ∵，设2()()3g x f x x ，则()()0g x g x ，∴()g x 为奇函数，又1()()62g x f x x ，∴()g x 在(0)x ，上是减函数，从而在R 上是减函数，又2(2)(2)12129f mf m m m ≤等价于22(2)3(2)(2)3(2)f m m f m m ≤，即(2)(2)g m g m ≤，22m m ∴≥，解得23m ≥，故选A ．二、填空题（本大题共4小题，每小题5分，共20分）题号13 14 15 16 答案[3)，21163π27862【解析】13．作出约束条件对应的平面区域，当目标函数2y x z 经过点(1，1)时，z 取得最小值3，故取值范围是[3)，．14．因为{bn}是等差数列，且16b ，1012b ，故公差2d ．于是*=28()n b n n N ，即128n n a a n ，所以87651646246(6)(4)(2)a a a a a …02463．98811a a ，1091021a a ．15．因为球与各面相切，所以直径为4，且11AC AB CB ，，的中点在所求的截面圆上，所以所求截面为此三点构成的边长为22的正三角形的外接圆，由正弦定理知263R ，所以面积8π3S ，以O 为顶点，以平面1A C B截此球所得的截面为底面的圆锥体积为18π116343π33627V ．16．2()2f x ax bx c ，由题意，()0f x ≥在R 上恒成立，∴00.a，≤即0a ，2.b ac ≤222221232323231b b b a ba b c a ab b a aa b b a b a ab a a ∴≥，令1bt a ，则221233(1)8(1)663(1)862+8111t tt t t t t t ≥，当且仅当12t 时，等号成立．三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤）17．（本小题满分12分）解：（Ⅰ）由3c ，且(3)(sin sin )()sin a C A b a B ，又根据正弦定理，得()()()c a c a b a b ，化简得，222ab c ab ，故2221cos 22b a c C ba ，所以60C ．……………………………………………………………………………（6分）（Ⅱ）由3c ，4sin 5A ，sin sin ac A C 得85a ，由a c ，得A C ，从而3cos 5A ，故433sin sin()sin cos cos sin 10B A C A CA C ，所以ABC △的面积为18318sin 225S ac B ．……………………………………（12分）18．（本小题满分12分）解：（Ⅰ）设图中从左到右的前3个小组的频率分别为23x x x ，，，则23(0.0370.013)51x x x ，解得0.125x，∵第2小组的频数为15，频率为20.25x，∴该校报考飞行员的总人数为：150.25=60（人）．…………………………………（6分）（Ⅱ）体重超过65公斤的学生的频率为(0.0370.013)50.25，∴X 的可能取值为0，1，2，3，且1~34X B ，，303327(0)C 464P X ，21133127(1)C 4464P X ，1223319(2)C 4464P X ，33311(3)C 464P X ，∴X 的分布列为：X0 1 2 3 P27642764964164由于1~34X B ，，13()344E X ．………………………………………………（12分）19．（本小题满分12分）（Ⅰ）证明：由已知得113AM AD ，如图，取BP 上靠近P 的四等分点T ，连接AT TN ，，由3NC PN 知//TN BC ，114TN BC ．……………………………………………（3分）又//AD BC ，故TN 平行且等于AM ，四边形AMNT 为平行四边形，于是//MN AT ．因为AT 平面PAB ，MN 平面PAB ，所以//MN 平面PAB ．…………………（6分）（Ⅱ）解：如图，取BC 的中点E ，连接AE ．由AB AC 得AE BC ，从而AE AD ，且222252BCAE AB BE AB ．以A 为坐标原点，AE 的方向为x 轴正方向，建立如图所示的空间直角坐标系A xyz ．由题意知，(004)P ，，，(520)B ，，，(010)M ，，，(520)C ，，，51342N ，，，(524)PB ，，，(010)AM ，，，51342AN ，，．设()n x y z ，，为平面AMN 的一个法向量，则00n AM n AN ，，即0513042y x y z，，……………………………………………（10分）可取5403n ，，．于是||16745|cos |745||||n PB n PB n PB ，，所以直线PB 与平面AMN 所成角的正弦值为16745745．……………………………（12分）20．（本小题满分12分）解：（Ⅰ）设M N ，为短轴的两个三等分点，因为△MNF 为正三角形，所以3||||2OF MN ，321323bb ，解得，2214a b ，因此，椭圆C 的方程为22143x y ．……………………………………………………（4分）（Ⅱ）设11()A x y ，，22()B x y ，，()P x y ，，AB 的方程为(3)y k x ，由22(3)143y k x x y ，，整理得2222(34)2436120k x k x k ，由24222448(34)(31)0k k k ，得235k ，221212222436123434k k x x x x k k ，，1212()()OA OB x x y y t x y ，，，则2121222124118()()(34)(34)k kx x x y y y t t k t t k ，，由点P 在椭圆上，得222222222(24)(18)+14(34)3(34)k k t k t k ，化简得22236(34)k t k ，………………………………………………………………（8分）因为||3PAPB ，所以2121||3k x x ，即221212(1)[()4]3k x x x x ，即2222222(24)4(3612)(1)3(34)34k k k k k ，即429656390k k，所以2283724k ，………………………………………（10分）即228373245k ，因为22236(34)k t k ，所以2222362793434kt kk ，所以2202834t ，即2t 的取值范围为(202834)，．………………………（12分）21．（本小题满分12分）（Ⅰ）解：2211()(0)a ax f x x x xx ，当0a ≤时，()0(0)f x x ，()f x 在(0)，上单调递减．当0a 时，由()0f x ，得1x a ，10x a ，时，()0f x ，()f x 在10a ，上单调递减，1x a ，时，()0f x ，()f x 在1a ，上单调递增．………………………………………………………………（5分）（Ⅱ）证明：要证4222(1)ln 1ln 2ln (2)4n n n n n n n n *≥，N ，即证42223(1)ln 1ln 2ln (2)4n n n n n *≥，N ．由（Ⅰ）知，当1a 时，()f x 在(01)，上单调递减，在(1)，上单调递增．1()ln 1(1)0f x x f x ≥，∴1ln 1x x ≥，∴221ln 1x x ≥，∴222222111ln1ln 2ln 11112n n ≥，∴2221112ln12ln 22ln 12n nn ≥．又2221111111+++121223(1)n n n ，∴2221111111+++121223(1)n n n n n 211111(1)11+++2231n n n n n ，∴2(1)ln1ln 2ln 2n n n ．………………………………………………………（9分）由柯西不等式，2222222(ln 1ln 2ln )(111)(ln1ln 2ln )n n ≥．∴4222231(1)ln 1ln 2ln (ln1ln 2ln )4n n n n n ≥+．∴42223(1)ln 1ln 2ln 4n n n ，∴4222(1)ln 1ln 2+ln (2*)4n n n n n n n n N ≥，．…………………………………（12分）22．（本小题满分10分）【选修4-4：坐标系与参数方程】解：（Ⅰ）将参数方程转化为一般方程1(3)l y k x ：，①21(3)3l y x k ：，②①×②消k 可得：2213x y．即P 的轨迹方程为221(0)3x y y ．1C 的普通方程为221(0)3x y y ．1C 的参数方程为3cos sin x y ，，（为参数πk k Z ，）．………………………（5分）（Ⅱ）由曲线2C ：πsin 424得：2(sin cos )422，即曲线2C 的直角坐标方程为：80x y ，由（Ⅰ）知曲线1C 与直线2C 无公共点，曲线1C 上的点(3cos sin )Q ，到直线80xy 的距离为π2sin 83|3cos sin 8|22d ，所以当πsin13时，d 的最小值为32．………………………………………（10分）23．（本小题满分10分）【选修4-5：不等式选讲】解：（Ⅰ）由题意可得10()130111x x g x x x x x ，≤，，，，≥，因为()4g x ，由图象可得不等式的解为53x ，所以不等式的解集为{|53}x x ．……………………………………………………（5分）（Ⅱ）因为存在1x R ，也存在2x R ，使得12()()f x g x 成立，所以{|()}{|()}y yf x x y yg x x R R ，，，又()|2||25||(2)(25)||5|f x x a x x a x a ≥，当且仅当(2)(25)0x a x ≤时等号成立.由（Ⅰ）知，max ()1g x ，所以|5|1a ≤，解得64a ≤≤，所以实数a 的取值范围为[64]，．…………………………………………………（10分）。

西南名校联盟（云南师大附中）2018届适应性月考卷（4）理科数学一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，则为（）A. B. C. D.【答案】A【解析】求解一元二次不等式可得：，由补集的定义可得：，结合并集的定义有：.本题选择A选项.2. 已知复数，则（）A. 0B. 1C.D.【答案】C【解析】由复数的运算法则有：.本题选择C选项.3. 在中，若原点到直线的距离为1，则此三角形为（）A. 直角三角形B. 锐角三角形C. 钝角三角形D. 不能确定【答案】A【解析】由已知可得：，故三角形为直角三角形.本题选择A选项.4. 已知点是所在平面内一点，为边的中点，且，则（）A. B. C. D.【答案】B【解析】因为为边的中点，.本题选择B选项.5. 已知是定义在上的奇函数，且满足，当时，，则等于（）A. B. C. -1 D. 1【答案】B【解析】由函数满足知的周期为4，又是定义在上的奇函数，故，.本题选择B选项.6. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．如图是源于其思想的一个程序框图，若输入的分别7，3，则输出的（）A. 6B. 5C. 4D. 3【答案】D【解析】时，不满足；时，不满足；时，满足，输出，本题选择D选项.点睛：此类问题的一般解法是严格按照程序框图设计的计算步骤逐步计算，逐次判断是否满足判断框内的条件，决定循环是否结束．要注意初始值的变化，分清计数变量与累加(乘)变量，掌握循环体等关键环节．7. 已知是函数的零点，若，则的值满足（）A. B. C. D. 的符号不确定【答案】B【解析】函数在是增函数，故零点是唯一的，又，则.本题选择B选项.8. 如图为一几何体的三视图，则该几何体的表面积为（）A. B. C. D.【答案】D【解析】如图所示，在长宽高分别为的长方体中，，则题中三视图对应的几何体是一个由图中的三棱柱和三棱锥组成的组合体，故其表面积为：，本题选择D选项.点睛：(1)以三视图为载体考查几何体的表面积，关键是能够对给出的三视图进行恰当的分析，从三视图中发现几何体中各元素间的位置关系及数量关系．(2)多面体的表面积是各个面的面积之和；组合体的表面积应注意重合部分的处理．(3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展为平面图形计算，而表面积是侧面积与底面圆的面积之和．9. 若将函数的图象向左平移个单位，平移后所得图象的对称中心为点，则函数在上的最小值是（）A. B. C. D.【答案】C【解析】，所以将的图象向左平移个单位后，得到的图象，其对称中心为点，，即：，取可得，函数的解析式为，的最小值是.本题选择C选项.10. 已知一个几何体下面是正三棱柱，其所有棱长都为；上面是正三棱锥，它的高为，若点都在一个体积为的球面上，则的值为（）A. B. 1 C. D.【答案】A【解析】设外接球的半径为，下底面外接圆的半径为，则，又，.本题选择A选项.点睛：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.11. 已知数列满足是其前项和，若，（其中），则的最小值是（）A. B. 5 C. D.【答案】D【解析】由题意，，以上各式相加得：，又，，学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...当且仅当时等号成立.本题选择D选项.12. 设过曲线（为自然对数的底数）上任意一点处的切线为，总存在过曲线上一点处的切线，使得，则实数的取值范围为（）A. B. C. D.【答案】C【解析】设的切点为，的切点为，由题意，对任意存在使得，对任意均有解，故对任意恒成立，则对任意恒成立．又.本题选择C选项.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 圆关于直线对称的圆的标准方程为__________．【答案】【解析】圆的圆心坐标为，它关于直线的对称点坐标为，即所求圆的圆心坐标为，所以所求圆的标准方程为．14. 二项式的展开式中项的系数为，则__________．【答案】【解析】，令，得．15. 已知实数满足约束条件，则的取值范围是__________．【答案】【解析】绘制不等式组表示的平面区域如图所示，由不等式组所表示的平面区域知：点到点的距离最大，故；点到直线的距离最小，即，所以的取值范围是．点睛：(1)本题是线性规划的综合应用，考查的是非线性目标函数的最值的求法．(2)解决这类问题的关键是利用数形结合的思想方法，给目标函数赋于一定的几何意义．16. 空间点到平面的距离定义如下：过空间一点作平面的垂线，这个点和垂足之间的距离叫做这个点到这个平面的距离.已知平面两两互相垂直，点，点到的距离都是2，点是上的动点，满足到的距离是到点距离的2倍，则点的轨迹上的点到的距离的最大值是__________．【答案】【解析】如图所示，在正方体中，平面对应平面，点位于平面内满足题意，原问题等价于在平面直角坐标系中有点，存在点到轴的距离为该点到点距离的2倍，求该点到轴的距离的最大值. 设，由题意得：，整理得：，所以所求最大值为．三、解答题（共70分.解答应写出文字说明、证明过程或演算步骤.）17. 在各项均为正数的等比数列中，是与的等差中项，若.（1）求数列的通项公式；（2）若数列满足，求数列的前项和.【答案】(1)；(2).【解析】试题分析：（1）由题意结合等差数列的性质可得，结合等差中项的性质可得，则，（2）由（1）得，，分组求和可得数列的前项和试题解析：（1）设等比数列的公比为，且，由得，又是与的等差中项，故或（舍）．所以，（2）由（1）得，，所以数列的前项和：18. 如图，在平面四边形，和都是等腰直角三角形且，正方形的边.（1）求证：平面；（2）求二面角的余弦值.【答案】(1)证明见解析；(2).【解析】试题分析：（1）由线面垂直的判断定理可得平面则由平面几何知识可得，据此有平面．（2）由题意可知AD，AB，AE两两垂直．建立空间直角坐标系，设AB=1，据此可得平面BDF的一个法向量为，取平面ABD的一个法向量为，则二面角的余弦值为．试题解析：（1）正方形中，又且，所以又因为和都是等腰直角三角形，所以，即，且，所以．（2）因为△ABE是等腰直角三角形，所以，又因为，所以，即AD，AB，AE两两垂直．建立如图所示空间直角坐标系，设AB=1，则AE=1，，，设平面BDF的一个法向量为，可得，取平面ABD的一个法向量为，则，故二面角的余弦值为．19. 甲乙两人进行跳棋比赛，约定每局胜者得1分，负者得0分.若其中的一方比对方多得2分或下满5局时停止比赛.设甲在每局中获胜的概率为，乙在每局中获胜的概率为，且各局胜负相互独立.（1）求没下满5局甲就获胜的概率；（2）设比赛结束时已下局数为，求的分布列及数学期望.【答案】(1)；(2)答案见解析.【解析】试题分析：（1）没下满局甲就获胜有两种情况：①两局后甲获胜，此时，②四局后甲获胜，此时，则满足题意的概率值为（2）由题意知的所有取值为：，，，据此可得的分布列，计算其数学期望为．试题解析：（1）没下满局甲就获胜有两种情况：①两局后甲获胜，此时，②四局后甲获胜，此时，所以，没下满5局甲就获胜的概率（2）由题意知的所有取值为则：，，，的分布列为:．20. 已知函数.（1）若，则当时，讨论的单调性；（2）若，且当时，不等式在区间上有解，求实数的取值范围.【答案】(1)答案见解析；(2).【解析】试题分析：（1）函数的定义域为，且，．分类讨论可得：当时，在内单调递减；当时，在上单调递减，在上单调递增；当时，在上单调递减，在上单调递增．（2）原问题等价于当时，在区间上的最大值．且，则.分类讨论和两种情况可得．据此求解关于实数a的不等式可得实数的取值范围是．试题解析：（1）函数的定义域为，由得，所以．当时，，在内单调递减；当时，或，所以，在上单调递减，在上单调递增；当时，或，所以，在上单调递减，在上单调递增．（2）由题意，当时，在区间上的最大值．当时，，则.①当时，，故在上单调递增，；②当时，设的两根分别为，则，所以在上，故在上单调递增，．综上，当时，在区间上的最大值，解得，所以实数的取值范围是．点睛：导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，所以在历届高考中，对导数的应用的考查都非常突出，本专题在高考中的命题方向及命题角度从高考来看，对导数的应用的考查主要从以下几个角度进行：(1)考查导数的几何意义，往往与解析几何、微积分相联系．(2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数．(3)利用导数求函数的最值(极值)，解决生活中的优化问题．(4)考查数形结合思想的应用．21. 已知椭圆的左、右焦点分别是，其离心率，点为椭圆上的一个动点，面积的最大值为3.（1）求椭圆的标准方程；（2）已知点，过点且斜率不为0的直线与椭圆相交于两点，直线，与轴分别相交于两点，试问是否为定值？如果，求出这个定值；如果不是，请说明理由.【答案】(1)；(2)答案见解析.【解析】试题分析：（1）由题意得到关于b,c的方程组，求解方程组结合椭圆的性质可得，则椭圆的标准方程为．（2）设直线的y轴截距式方程：，结合直线方程可得，．联立直线方程与椭圆方程有，结合韦达定理可得，则为定值.试题解析：（1）由题意知，当点是椭圆的上、下顶点时，的面积最大，此时的面积，①又椭圆的离心率，②由①②得：，所以，椭圆的标准方程为．（2）设直线的方程为，则直线的方程为，则，即，同理可得．由得，由得且，所以，故为定值．点睛：解决直线与椭圆的综合问题时，要注意：(1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件；(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三角形的面积等问题．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. 在平面直角坐标系中，直线的参数方程为：（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.（1）求直线的普通方程与曲线的直角坐标方程；（2）设曲线与直线交于两点，若点的坐标为，求．【答案】(1)，；(2).【解析】试题分析：（1）消去参数可得直线的普通方程为，极坐标化为直角坐标可得曲线的直角坐标方程为．（2）将直线的参数方程代入曲线的直角坐标方程，可得，结合参数方程的几何意义可知．试题解析：（1）由直线的参数方程：得直线的普通方程为，由得，配方得，即曲线的直角坐标方程为．（2）将直线的参数方程代入曲线的直角坐标方程，得，即，因为，所以可设是点所对应的参数，则．又直线过点，所以．23. 已知，若不等式的解集为.（1）求实数的值；（2）若对一切实数恒成立，求实数的取值范围.【答案】(1)；(2).【解析】试题分析：(1)求解绝对值不等式，据此得到关于实数t的方程，解方程可得．（2）由（1）知，，由绝对值三角不等式的性质可得，当且仅当时等号成立，则实数的取值范围为．试题解析：（1）由得，解得或，由题意所以．（2）由（1）知，，所以，当且仅当时等号成立，所以，故实数的取值范围为．。

云南师大附中2018届高考适应性月考卷（五）语文参考答案1．（3分）C【解析】A项，原文说的是，“从海外传播的视角，我们可以将中华文化分为‘硬文化’和‘软文化’”。

B项，“融入民族精神、伦理道德等‘软文化’”是为了传播“软文化”，以“硬”促“软”。

D 项，“也要认识到我国文化的进步性与优越性”不正确，原文说的是传播者必须“认识到各种文化各有千秋，没有高低优劣之分”。

2.（3分）D【解析】“分别提供了例证”不正确。

3.（3分）B【解析】“‘硬文化”的传播“可以拓展‘软文化’传播的渠道”，但并不是“只有借助‘硬文化’，‘软文化’才能实现有效传播”。

4.（3分）C【解析】后文中写道“我无论如何也没想到”“三叔说的竟然是”，可见“我”并没有料想到。

5.（5分）①运用神态、动作、语言和细节等多种描写手法，揭示出三叔的狂喜和乐极生悲。

描写细腻生动，富有戏剧效果。

②比喻，作者把三叔皮肉里含着的笑容比作还没有绽放的花骨朵，生动刻画了其在听到“我”的问题后，情感上由喜悦转向迷惘的微妙变化。

（描写手法答出两种给3分，答出比喻给2分）6.（6分）①强调了袁五谷和袁丰登两人之间的仇恨之深。

②引起读者的好奇心，为什么不是人？吸引读者去阅读文章，寻找答案。

③与文章最后“记不清”的答案形成鲜明对照，突显了这种仇恨的荒唐可笑。

（每点2分）7.（3分）B【解析】“主要原因”错，从材料一的内容来看，“考生凭高考成绩即可报考部分国外大学”确实可以增强其竞争力，但不一定是“出国留学人数创出历史新高的主要原因”。

8.（5分）AE【解析】B项，“但总体呈现大规模下降趋势”依据不足。

C项，因果倒置。

D项，依据材料三，是“清华大学”将从2017年起全面推行大类招生模式，并非我国。

9．（4分）外部原因：①出生人口减少。

②出国留学人数增加。

③国外高校的有力竞争。

内部原因：部分专业的社会认可度不高。

（共四点，每点1分）10．（3分）C 【解析】“昔周以冢宰制”缺宾语，这句的宾语是“国用”，“量入为出”为常见成语。

云南师大附中 2018 届高考适应性月考卷（一） 理科综合参考答案
一、选择题：本题共 13 小题，每小题 6 分。 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 答案 C D A B D C A B D C B C D
二、选择题：本题共 8 小题，每小题 6 分。在每小题给出的四个选项中，第 14～18 题只有一 项符合题目要求；第 19～21 题有多项符合题目要求，全部选对的给 6 分，选对但不全的给 3 分，有选错的给 0 分。
理科综合参考答案·第 1 页（共 13 页）
6．细菌无染色体，不会发生染色体变异。基因突变具有随机性的特点。抗生素的滥用在超级
细菌进化过程中的作用是使种群基因频率发生定向改变，从而决定进化方向。新物种形成
的标志是生殖隔离的产生。
7Hale Waihona Puke 硅胶多孔吸附水分，没有发生化学变化，A 正确。
8．应该为 2−甲基丁烷，A 错误。甲基中最多只有 1 个 H 在面上，故最多有 7 个原子共面，B
左手定则知， 0 ~ t0 安培力沿右下方，故水平力沿左方向，为负向，故 C 错误。
19 ． 向 上 做 匀 加 速 直 线 运 动 时 ， 由 F (m1 m2 )g (m1 m2 )a 和 kx1 m2 g m2a 可 得
，D
错误。
11．分析题意可知：X、Y、Z、W 分别为 O、Na、S、Cl。核外电子排布相同时，核电荷数越 大，离子半径越小，故离子半径：Y<X，A 错误。同周期（除稀有气体元素外）从左到右 非金属性递增，故非金属性：Z<W，B 正确。水分子间形成氢键，故沸点：Z<X，C 错误。 应该是最高价氧化物对应水化物的酸性，D 错误。
17．滑片 P 向下缓慢滑动时，变阻器电阻 R 减小，U1 不变，故 I2 增大， R0 两端电压增大，U2

云南师⼤附中2018届⾼考适应性⽉考卷（⼆）语⽂-答案语⽂参考答案·第1页（共4页）云南师⼤附中2018届⾼考适应性⽉考卷（⼆）语⽂参考答案1.（3分）D 【解析】A 项曲解⽂意，出处见第⼀段：对“阿尔法狗”和它的发明者来说，⽐赢得⽐赛更重要的，是寻找⼈⼯智能的科学真理。

B 项强加因果。

C 项以偏概全且曲解⽂意，出处见原⽂第三段“⼈⼯智能遭遇的技术瓶颈，⼀⽅⾯有着时代的限制，另⼀⽅⾯也是由于⼈们对它的期待太⾼”。

2.（3分）C 【解析】C 项⽆中⽣有，⽂章没有明确表⽰中国能引领浪潮。

3.（3分）B 【解析】B 项曲解⽂意，出处见第⼆段：因此也有科学家认为，“我们或许是和⼈⼯智能真正共同⽣活的第⼀代⼈”。

4.（3分）C 【解析】C 项概括不准确，根源是⽂中说“⼀个⽼专家，不是说空话的⼈”，因此得到村民真⼼的拥戴。

5.（5分）①“我”是故事的讲述者，也是见证者，“我”见证了上个世纪⽼知识分⼦踏实肯⼲，扎根农村，⾝体⼒⾏为祖国做贡献的精神品质。

第⼀⼈称叙事增加了⽂章的真实性和可信度；②“我”是线索⼈物，推动故事发展，使⽂章情节连贯，有始有终。

（第①点3分，第②点2分）6.（6分）①“⽊雏”本是20年前圆湖村⼈对⽂中⽼师的性格的直观认识，“⽊”就是不活泛，见⼈不会说话，不知道招呼。

“雏”是幼稚。

②“⽊雏”反映出⽂中⽼师勤学善问，⼼⽆旁骛致⼒于学，扎根农村为民服务的知识分⼦形象。

③“⽊雏”揭⽰⼩说主旨：农村发展、现代化建设都需要潜⼼研究，不说空话的钻研和学习，时代需要“⽊雏”精神。

（每点2分）7.（3分）B 【解析】B 项曲解⽂意,出处见材料三：由于经济实⼒有限，很多地⽅“⼀级政府建设并管理⼀级图书馆”的做法逐渐演变成“⼀级政府建设并管理⼀个图书馆”。

8.（5分）CE （选C 得3分，选E 得2分）【解析】A 项曲解⽂意，出处见材料⼀“但相对快速发展的经济社会、⽇益增长的⼈民群众精神⽂化需要，仍存在总量不⾜、经费不⾜、地区不平衡、城乡不平衡以及国际化⽔平较低等问题”；B 项增长量最⼩的是2007年和2011年。

云南省师范大学附属中学2018届高三高考适应性月考卷（三）数学（理）试题注意事项：1.答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。

2.每小题选出答案后，用2B 铅笔把答题卡上对应科目的答案标号涂黑，如需改动，用橡皮才干净后，再选涂其他答案标号，在试题卷上作答无效。

3.考试结束后，请将本卷和答题卡一并交回，满分150分，考试用时120分钟。

一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知集合{},3,2,1,0,1,2--=A 集合{},32x y x B -==则B A ⋂中元素的个数为 A.2 B.3 C.4 D.52.复数z 满足5)2)(3(=+-i i z （i 为虚数单位），则z 的共轭复数等于 A.-2-2i B.-2+2i C.2-2i D.2+2i3.祖恒原理：“幂势既同，则积不容异”，它是中国古代一个涉及集合体体积的问题，意思是两个等高的几何体，如在同高处的截面积恒相等，则体积相等，设A,B 为两个等高的几何体，P ：A ，B 的体积相等，q:A ，B 在同高处的截面积不恒相等，根据祖恒原理可知，q 是p 的A.充分不必要条件B.必要不充分条件C.充分条件D.既不充分也不必要条件 4.522)11)(3(-+xx 的展开式的常数项是 A.-3 B.-2 C.2 D.35.已知双曲线)0,0(12222〉〉=-b a by a x 的一条渐进线方程为x y 23=，且双曲线的一个焦点在抛物线x y 742-=的准线上，则双曲线的方程为A.13422=-y xB.14322=-y xC.1212822=-y xD.1282122=-y x6.已知函数),62cos(2sin )(π+-=x x x f 则下列结论正确的是A.导函数为)62cos(3)(π-=x x fB.函数)(x f 的图象关于直线2π=x 对称C.函数)(x f 在区间)3,6(ππ-上是增函数 D.函数)(x f 的图象可由函数x y 2sin 3=的图象向右平移6π个单位长度得到 7.执行如图1所示的程序框图，如果输出的n 的值为4，则输入的a 的值可以为 A.1 B.2 C.3 D.48.已知单调递减的等比数列{}n a 满足：,28432=++a a a 且23+a 是42,a a 的等差中项，则{}n a的前6项和为A.63B.64C.1D.1269.已知直三棱柱111C B A ABC -的6个顶点都在表面积为π100的球0的球面上，若34,4===BC AC AB ，则该三棱柱的体积为A.38B.312C.213D.324 10.设21,F F 分别是椭圆)0(1:2222〉〉=+b a by a x C 的左、右焦点，过1F 的直线l 交椭圆于A,B两点，l 在y 轴上的截距为1，若B F F A 113=，且x AF ⊥2轴，则此椭圆的长轴长为A.33B.3C.6D.6图111. 在等腰梯形ABCD 中，已知AB ∥DC ，AB =2，BC =1，=∠ABC 60°，动点E 和F 分别在线段BC 和DC 上，且DC DF BC BE λλ41,==,则AF AC ⋅的最小值为 A.1829 B.87 C.1817 D.815 12. 设函数)(x f 在R 上存在导函数),(1x f 对于任意的实数x ，都有),(6)(2x f x x f --=当)0,(-∞∈x 时，,91212)2()2(,121)(221m m m f m f x x f -++-≤+〈+若则实数m 的取值范围是 A.⎪⎭⎫⎢⎣⎡+∞-,32 B.⎪⎭⎫⎢⎣⎡+∞-,21 C.[)+∞-,1 D.[)+∞-,2二、填空题（本大题共4小题，每小题5分，共20分）13. 已知实数y x ,满足条件y x z x y x x y +=⎪⎩⎪⎨⎧≥≥+≥2,1,1,则的取值范围是 。

语文试卷注意事项：1.答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚。

2.每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

在试题卷上作答无效。

3.考试结束后，请将本试卷和答题卡上一并交回。

满分150分，考试用时150分钟。

一、现代文阅读（35分）（一）论述类文本阅读（9分，每小题3分）阅读下面的文字，完成1-3题。

‚任务驱动型作文‛源自于西方国家日常语言教学和写作教学的‚任务型语言教学法‛，这种语言教学法是基于建构主义理论而提出的，其核心是在明确‚任务‛的前提下，完成语言交际口语或书面语表达。

这种教学法，根据完成任务过程中所产生的互相影响把任务分成五类：拼板式任务，要求学生把散乱的若干信息拼成一个整体；信息差任务，给两个或两组学生有互补作用的信息，为了完成交际任务，双方必须协商以探清对方的信息；解决问题式任务，给学生一个问题及一系列信息，让其找到一个解决问题的方案；做决定式任务，给学生一个可能有几种结局的问题，让他们通过协调和讨论选择一种结果，进行论述；交换意见式任务，学生参与讨论、交换意见，但无须达成一致。

国内一些学者在‚任务型语言教学法‛的基础上，增加‚驱动‛一词，用于作文教学。

教育部考试中心的张开明确提出了2015年高考作文的两道题目均属于‚任务驱动型作文‛，并对其概念做出阐释：‚试题往往是给学生创作出一个情境，出现对立性的问题，让考生通过写作，提出解决处理问题的想法和方案……如今年作文中‘写信’‘权衡与选择’等任务型指令，着力发挥试题引导写作任务的功能，使考生在真实的情境中辨析关键概念，在多维度的比较中说理论证。

‛他认为，在材料型作文中增加任务驱动型指令，能‚较好地解决材料型作文的泛角度与阐释型作文收缩性之间的矛盾‛，是在承继材料作文‚自主空间大、立意角度自然、多元‛等传统优势的基础上，又在避免套作、宿构方面进行了新的尝试和探索。

云南师大附中 2018 届高考适应性月考卷（八） 文科数学参考答案
一、选择题（本大题共 12 小题，每小题 5 分，共 60 分） 题号 答案 【解析】 1．由题意知：集合 A [3，3] ，集合 B (，2) ，则 A B [3，2) ，故选 D． 2．在复平面内， z 的轨迹是以 (1， 1) 为圆心，1 为半径的圆，由数形结合可知， | z | 的最小值 为 2 1 ，所以 | z |2 3 2 2 ，故选 B． 由数列 {an } 为等差数列， 设其公差为 d ， 所以 (a2 a4 a6 ) (a1 a3 a5 ) 3d 3 ， 即 d 1， 3． 故选 A． 1 D 2 B 3 A 4 A 5 C 6 B 7 B 8 D 9 B 10 C 11 A 12 C
5．由题意可知圆柱的高为 2，所以球心到底面的距离为 1，又由底面的半径为 1，所以圆柱的
外接球的半径为 2 ，故而圆柱的外接球的表面积为 8π ，故选 C．
π 6．由函数 f ( x) 的最大值为 4 ，则选项 A 不满足；由 ，2 为其一个对称中心，即 3 选项 D 不满足；由 f ( x1 ) f ( x2 ) 2 ，且 | x1 x2 |min 不满足；而 B 选项均满足，故选 B．
图1
内切圆的直径为 6 步，故选 B．
文科数学参考答案·第 1 页（共 9 页）
8． 到正四面体的四个顶点距离相等的截面， 如图 2 有两种情况：第一种情况，截面为边长为 1 的正三角形，共有 4 种情况；第二种情况， 截面为边长为 1 的正方形，共有 3 种情况，综
图2
上所述，所有截面的个数为 3 4 7 ，故选 D． 9．由 x，y，z 均为大于 1 的正数，令 log 2 x log 3 y log 5 z m ，则 m 0 ，且 x 2m ， y 3m ，

云南师大附中2018届高考适应性月考卷（六）文科数学参考答案一、选择题（本大题共12小题，每小题5分，共60分）【解析】1．由题有{|0}M y y =>，{|}N y y =∈R ，∴{|0}M N y y => ，故选C ． 2．∵向量a ，b的夹角θ的取值范围为[0π]，，故选A ．3．原式1132216⎛⎛⎫=-⨯= ⎪ ⎝⎭⎝⎭，故选B. 4．由2018i(1i)i z ++=-有(1i)1i z +=-，∴1i1i z -=+2(1i)2i i (1i)(1i)2--===-+-，故选D ． 5．设5()2f x x =+，由5(4)(4)20f -=-+<，5(2)(2)20f -=-+<，(0)20f =>，由(4)(2)0f f -->，(2)(0)0f f -<，得下一个有根的区间是(20)-，，故选D.6．1()1(0)f x x x '=+>，∴函数()f x 在点(1(1))f ，处的切线斜率为(1)22af '=-， ∴252a-=，得6a =-，故选A. 7．抛物线22x py =(0)p >的标准方程为212y x p=，故选C ． 8．∵0k ≠，由22sin 1k x k =+有21sin 2k x k +=，而212||k k +≥，|sin |1x ≤，∴1k =±，故选D.9．∵()A a b ，，(e )B c ，在()ln f x x =的图象上，∴ln b a =，ln e 1c ==，∴1b b c +=+= l n l n e l n a a +=，∴(e 1)a b +，一定在()f x 的图象上，故选B ． 10．由题有22222214c y a b y c ⎧+=⎪⎨⎪=⎩，，而222a b c =+，∴222ac a c =-，得221e e =-，由01e <<得1e ，故选B ．11．2{log 1}0=，2{log 2}1=，22{log 3}{log 4}2==，2222{log 5}{log 6}{log 7}{log 8}3====，22{log 9}{log 10}4==，∴122432425S =+⨯+⨯+⨯=，故选A ．12．如图1，该几何体是一个正方体截去两个三棱锥后余下的部分，故该几何体的体积为32V =-11212232⨯⨯⨯⨯⨯320cm 3=，故选C ．二、填空题（本大题共4小题，每小题5分，共20分）【解析】13．∵3100a b m =+=，∴97m =．14．作出不等式组表示的可行域如图2阴影部分，由AC OB ⊥得2AB OB ==，∴211π22π282S =-⨯⨯=-.15．球A 的表面积为4π，球B 的表面积为8π，球C 的表面积为12π，∴三个球的表面积之和为24π．16．由题有0k ≠，且1a b k +=，22221a b k k+=-，故2221[()()]2ab a b a b =+-+2211212k k k ⎡⎤⎛⎫=-- ⎪⎢⎥⎝⎭⎣⎦211k k =-，∴221111124z ab k k k ⎛⎫==-=-- ⎪⎝⎭，由22210R k k =->得102k<<，又圆心到直线的距离不大于圆的半径，故 2221k k -⎝⎭≤，即 1403k <≤，故1403k <≤，于是1449z ⎡⎤∈-⎢⎥⎣⎦，． 三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤）图1图217．（本小题满分12分）解：（Ⅰ）∵1357915a a a a a ++++=，24681025a a a a a ++++=，∴5515a =，6525a =，得53a =，65a =，∴2d =，………………………………（2分） ∴5(5)n a a n d =+-32(5)n =+-27n =-，……………………………………………（4分） 得15a =-，∴1(1)2n n n S na d -=+26n n =-．…………………………………………（6分）（Ⅱ）∵141b a ==，13n n n b b +-=，∴112211()()()n n n n n b b b b b b b b ---=-+-+⋅⋅⋅+-+ 123331n n --=++⋅⋅⋅++31(2)2n n -=≥，………………………………………………（10分）又13112b -==，∴31(*)2n n b n -=∈N ，故由6n n b S n =+得2312n n -=，∴1n =或2n =．……………………………………（12分） 18．（本小题满分12分）解：（Ⅰ）4679975x ++++==男生组，56681075x ++++==女生组，………………（2分）222222(47)(67)(77)(97)(97) 3.65s -+-+-+-+-==男生组，222222(57)(67)(67)(87)(107) 3.25s -+-+-+-+-==女生组，………………………（4分）由x x =男生组女生组知男生组与女生组的总体竞赛水平相同，由22s s >男生组女生组知男生组的竞赛水平差异比女生组的竞赛水平差异大．…………（6分） （Ⅱ）设该班从这次竞赛中随机选取一个“竞赛联合组”是“优秀联合组”为事件A ， 每个“竞赛联合组”的男生和女生答对的题目数组成的基本事件数有(45)，，(46)，，(46)，，(48)，，(410)，，(65)，，(66)，，(66)，，(68)，，(610)，，(75)，，(76)，，(76)，，(78)，，(710)，，(95)，，(96)，，(96)，，(98)，，(910)，，(95)，，(96)，，(96)，，(98)，，(910)，，共25种，事件A 包含的基本事件有11种，∴11()25P A =，故该班从这次竞赛中随机选取一个“竞赛联合组”是“优秀联合组”的概率是1125．……（12分） 19．（本小题满分12分）解：（Ⅰ）在折叠过程中，当平面BEC ⊥平面AECD 时，四棱锥B AECD -的体积最大． 如图3，取EC 的中点F ，连接BF ， ∵由题得BEC △为正三角形，∴BF EC ⊥，又平面BEC 平面AECD EC =， 故BF ⊥平面AECD ，得BF 是四棱锥B AECD -的体积最大时的高，由题得BFAC =2DE =，∴13B AECD AECD V S BF -= 菱形1132AC DE BF =⨯⨯⨯⨯11232=⨯⨯2=，∴四棱锥B AECD -的体积的最大值为2．……………………………………………（6分） （Ⅱ）当2λ=时，BC ∥平面.PDF证明如下：如图4，连接AC ，DF ，AC DF G = ，连接PG ，PF ，∵BC ⊂平面ABC ，PG ⊂平面ABC ，而BC ⊄平面PDF ，平面PDF 平面ABC PG =， 若BC ∥平面PDF ，则BC ∥PG ， 由于ADG △∽CFG △，∴2AD AGCF CG==，故由BC ∥PG ，得2AP AGPB CG==，即2AP PB =，∴2λ=．………………………（12分） 20．（本小题满分12分）（Ⅰ）证明：∵12x x ≠，有0m ≠，而22112288y x y x ==，, ∴线段AB 的斜率为2121AB y y k x x -=-21222188y y y y -=-218y y =+4m =， 图3图4∴线段AB 的垂直平分线方程为(2)4m y m x -=--，即(6)4my x =--， 可见点（6，0）的坐标满足以上方程而与m 的取值无关，故线段AB 的垂直平分线恒过定点，该定点的坐标为（6，0）.……………………（4分） （Ⅱ）解：由（Ⅰ）有(60)Q ，，0m ≠，直线AB 的方程为4(2)y m x m-=-， 由284(2)y x y m x m ⎧=⎪⎨-=-⎪⎩，得2222160y my m -+-=， ∵12y y ≠，∴22(2)4(216)0m m ∆=--->，得44m -<<，4004m m -<<<<故或， 又122y y m +=，212216y y m =-，∴||AB ==又点(60)Q ，到直线AB的距离||d QM ==∴1||2AQB S AB d =△ 设2(016)m t =∈，，23()2561625616h t t t t =⨯+--， 则2()256323h t t t '=--(316)(16)t t =-++， 令()0h t '=得16t =-(舍去)，163t =， 由于1603t <<时，()0h t '>，()h t 单调递增，16163t <≤时，()0h t '≤，()h t 单调递减， ∴当2163m t ==时，()h t 取得最大值，即AQB △的面积取得最大值， 故AQB △………………………………………………………………………………………（12分）21．（本小题满分12分）解：（Ⅰ）函数()f x 的定义域为(0)+∞，，()2a f x x x '=+22x ax+=，①若0a ≥，有()0f x '>，函数()f x 在(0)+∞，上单调递增； ②若0a <，有2()x x f x x⎛- ⎝⎭⎝⎭'=，∴当0x ⎛∈ ⎝⎭时，()0f x '<，函数()f x在0⎛ ⎝⎭上单调递减；当x ⎫∈+∞⎪⎪⎝⎭时，()0f x '>，函数()f x在⎫+∞⎪⎪⎝⎭上单调递增．………（4分） （Ⅱ）∵()(2)f x a x +≤对任意的[1e]x ∈，恒成立， 即2ln (2)a x x a x ++≤对任意的[1e]x ∈，恒成立， 即2(ln )2a x x x x --≥对任意的[1e]x ∈，恒成立． 令()ln g x x x =-，得1()1g x x '=-1x x-=， 当[1e]x ∈，时，()0g x '≥，函数()g x 在[1e ]，上单调递增； ∴()(1)10g x g =>≥，即ln 0x x ->，故得22ln x xa x x--≥．设22()ln x xh x x x-=-，[1e]x ∈，，∵221(22)(ln )(2)1()(ln )x x x x x x h x x x ⎛⎫----- ⎪⎝⎭'=-2(1)(2ln 2)(ln )x x x x x --+=-， 当[1e]x ∈，时，10x -≥，2ln 20x x -+>，∴()0h x '≥， 故函数()h x 在[1e ]，上单调递增， ∴2maxe 2e()(e)e 1h x h -==-， 故2e 2ee 1a --≥．…………………………………………………………………………（12分）22．（本小题满分10分）【选修4−4：坐标系与参数方程】解：（Ⅰ）由2cos cos ρρθθ=，得222cos cos ρρθρθ=，得曲线E的直角坐标方程为2y (0)a >，又直线l 的斜率为1-，且过点A ，故直线l的直角坐标方程为y x =-………………………………………………（5分）（Ⅱ）在直角坐标系xOy 中，直线l的参数方程为2x y ⎧=⎪⎪⎨⎪=⎪⎩，， (t 为参数)，代入2y 得22(4)4160t a t a ++++=，∴122(4)t t a +=-+，12416t t a =+，∵2||||||BC AB AC = ，∴21212()t t t t -= ，即21212()5t t t t += ，∴24(4)5(416)a a +=+，得2340a a +-=，由0a >，得1a =．…………………（10分）23．（本小题满分10分）【选修4−5：不等式选讲】解：（Ⅰ）∵()f x 在[2)+∞，上单调递增，且||32m +>， |4|22m -+≥， 故要使(||3)(|4|2)f m f m +>-+，只需||3|4|2m m +>-+，即只需|||4|1m m -->-， 当0m <时，有41->-，不成立，可知m ∈∅，当04m ≤≤时，有32m >，故342m <≤， 当4m >时，有41>-，故4m >，综上得实数m 的取值范围为32⎛⎫+∞ ⎪⎝⎭，．………………………………………………（5分） （Ⅱ）∵()(12][12)f x ∈-∞-+∞ ，，， 令()(12][12)y f x k y k k =+∈-∞-++∞ ，∴，，， 如果存在0x <使0y >，即12k >，则不能满足()4g x >对定义域内的所有x 恒成立，故有12k ≤，且函数定义域为(0)+∞，，则要使()4g x >对定义域内的所有x 恒成立，这时1216k +>，即4<≤．………………………………………………………………（10分）k>，∴412k。

云南师大附中2018届高考适应性月考卷（三）理科数学参考答案一、选择题（本大题共12小题，每小题5分，共60分）【解析】1．2{|{|30}[B x y x x ==-=≥，所以={101}A B - ，，，故选B ． 2．由题意知53i 22i 2i z =+=++，z 的共轭复数等于22i -，故选C ．3．q ⌝：A B ，在同高处的截面积恒相等，p A B ：，的体积相等，故q 是p ⌝的必要不充分条件，故选B ．4．5211x ⎛⎫- ⎪⎝⎭的展开式的通项为51521C (1)0r r r rT r x -+⎛⎫=-= ⎪⎝⎭ ，，1，2，3，4，5．当因式2(3)x +中提供2x 时，则取4r =；当因式2(3)x +中提供3时，则取5r =，所以5221(3)1xx ⎛⎫+-⎪⎝⎭的展开式的常数项是2，故选C ．5．双曲线22221(00)x y a b a b -=>>，的渐近线方程为b y x a =±，所以b a =，双曲线的一个焦点在抛物线2y =-准线方程x =上，所以c =2a b =，以双曲线方程为22143x y -=，故选A ．6．因为11π()sin 2sin 22cos22226f x x x x x x x ⎫⎛⎫=+=--⎪ ⎪⎪⎝⎭⎭，所以π()26f x x ⎛⎫'=- ⎪⎝⎭，故A 错误，当π2x =时，π5π2=66x -，故B 错误，对于D ，应向右平移π12个单位，故选C ．7．4n =时，31Q =，此时P Q >，则输入的a 的值可以为3，故选C ．8．设等比数列{}n a 的首项为1a ，公比为q ，依题意有：3242(2)a a a +=+，23428a a a ++=得38a =，故31123120=8a q a q a a q ⎧+=⎪⎨=⎪⎩，，解之得122a q =⎧⎨=⎩，或13212a q =⎧⎪⎨=⎪⎩，，又{}n a 单调递减，所以663S =，故选A ．9．由题意知，球O 的半径5R =，直三棱柱111ABC A B C -的底面外接圆半径为4，则直三棱柱111ABC A B C -的高为6，则该三棱柱的体积为D ．10．由题意，2225233b c b A c b a B a a ⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭，，，，，代入到椭圆方程整理得222225199c b a a +=，联立22b a =，解得3a =，故选D ．11．17115()()()48228AE AF AB BE AD DF AB BC AD DC λλλλ⎛⎫=++=++=++ ⎪⎝⎭ ≥，当且仅当122λλ=，即1λ=时取等号，故选D ．12．22()3()30f x x f x x -+--=∵，设2()()3g x f x x =-，则()()0g x g x +-=，∴()g x 为奇函数，又1()()62g x f x x ''=-<-，∴()g x 在(0)x ∈-∞，上是减函数，从而在R 上是减函数，又2(2)(2)12129f m f m m m +-++-≤等价于22(2)3(2)(2)3(2)f m m f m m +-+---≤，即(2)(2)g m g m +-≤，22m m +-∴≥，解得23m -≥，故选A ．二、填空题（本大题共4小题，每小题5分，共20分）【解析】 13．作出约束条件对应的平面区域，当目标函数2y x z =-+经过点(1，1)时，z 取得最小值3，故取值范围是[3)+∞，． 14．因为{bn}是等差数列，且16b =-，1012b =，故公差2d =．于是*=28() n b n n -∈N ，即128n n a a n +-=-，所以87651646246(6)(4)(2)a a a a a =+=++=+++==+-+-+-… 02463++++=．98811a a =+=，1091021a a =+=．15．因为球与各面相切，所以直径为4，且11AC AB CB ，，的中点在所求的截面圆上，所以所求截面为此三点构成的边长为由正弦定理知R =，所以面积8π3S =，以O 为顶点，以平面1A C B 截此球所得的截面为底面的圆锥体积为18π1336V =⨯⨯⨯．16．2()2f x ax bx c '=++，由题意，()0f x '≥在R 上恒成立，∴00.a >∆，≤即0a >，2.b ac ≤222221232323231b b b a b a b c a ab b a a a b b a b a ab a a ⎛⎫++++ ⎪++++⎝⎭==----∴≥，令1b t a =>，则221233(1)8(1)663(1)8111t t t t t t t t ++-+-+==-++---≥，当且仅当1t =成立．三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤）17．（本小题满分12分）解：（Ⅰ）由c =，且)(sin sin )()sin a C A b a B -=-，又根据正弦定理，得()()()c a c a b a b +-=-，化简得，222a b c ab +-=，故2221cos 22b a c C ba +-==， 所以60C =︒．……………………………………………………………………………（6分）（Ⅱ）由c 4sin 5A =，sin sin a c A C =得85a =，由a c <，得A C <，从而3cos 5A =，故sin sin()sin cos cos sin B A C A C A C =+=+=， 所以ABC △的面积为1sin 2S ac B ==．……………………………………（12分）18．（本小题满分12分）解：（Ⅰ）设图中从左到右的前3个小组的频率分别为23x x x ，，，则23(0.0370.013)51x x x ++++⨯=，解得0.125x =，∵第2小组的频数为15，频率为20.25x =，∴该校报考飞行员的总人数为：150.25=60÷（人）．…………………………………（6分） （Ⅱ）体重超过65公斤的学生的频率为(0.0370.013)50.25+⨯=，∴X 的可能取值为0，1，2，3，且1~34X B ⎛⎫ ⎪⎝⎭，， 303327(0)C 464P X ⎛⎫=== ⎪⎝⎭，21133127(1)C 4464P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， 1223319(2)C 4464P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，33311(3)C 464P X ⎛⎫=== ⎪⎝⎭， ∴X由于1~34X B ⎛⎫ ⎪⎝⎭，，13()344E X =⨯=．………………………………………………（12分） 19．（本小题满分12分）（Ⅰ）证明：由已知得113AM AD ==，如图，取BP 上靠近P 的四等分点T ，连接AT TN ，，由3NC PN =知//TN BC ，114TN BC ==．……………………………………………（3分）又//AD BC ，故TN 平行且等于AM ，四边形AMNT 为平行四边形，于是//MN AT ． 因为AT ⊂平面PAB ，MN ⊄平面PAB ，所以//MN 平面PAB ．…………………（6分） （Ⅱ）解：如图，取BC 的中点E ，连接AE ．由AB AC =得AE BC ⊥，从而AE AD ⊥，且AE ． 以A 为坐标原点，AE的方向为x 轴正方向，建立如图所示的空间直角坐标系A xyz -．由题意知，(004)P ，，，20)B -，，(010)M ，，，20)C ，，132N ⎫⎪⎪⎝⎭，，，24)PB =-- ，，(010)AM = ，，，132AN ⎫=⎪⎪⎝⎭ ，，．设()n x y z =，，为平面AMN 的一个法向量，则00n AM n AN ⎧=⎪⎨=⎪⎩ ，，即01302y y z =⎧++=，，……………………………………………（10分）可取40n ⎛= ⎝⎭ ，，．于是|||cos |||||n PB n PB n PB 〈〉== ，，所以直线PB 与平面AMN所成角的正弦值为．……………………………（12分）20．（本小题满分12分）解：（Ⅰ）设M N ，为短轴的两个三等分点，因为△MNF 为正三角形，所以|||OF MN =，213b b == ，解得2214a b =+=， 因此，椭圆C 的方程为22143x y +=．……………………………………………………（4分）（Ⅱ）设11()A x y ，，22()B x y ，，()P x y ，，AB 的方程为(3)y k x =-， 由22(3)143y k x x y =-⎧⎪⎨+=⎪⎩，，整理得2222(34)2436120k x k x k +-+-=， 由24222448(34)(31)0k k k ∆=-+->，得235k <， 221212222436123434k k x x x x k k -+==++，， 1212()()OA OB x x y y t x y +=++= ，，， 则2121222124118()()(34)(34)k k x x x y y y t t k t t k -=+==+=++，， 由点P 在椭圆上，得222222222(24)(18)+14(34)3(34)k k t k t k -=++，化简得22236(34)k t k =+，………………………………………………………………（8分）因为||PA PB -<12|x x -，即221212(1)[()4]3k x x x x ++-<， 即2222222(24)4(3612)(1)3(34)34k k k k k ⎛⎫-+-< ⎪++⎝⎭， 即429656390k k +->，所以2k ，………………………………………（10分）即235k <<，因为22236(34)k t k =+， 所以2222362793434k t k k ==-++，所以2204t <，即2t的取值范围为(204)．………………………（12分） 21．（本小题满分12分） （Ⅰ）解：2211()(0)a ax f x x x x x -'=-=>，当0a ≤时，()0(0)f x x '<>，()f x 在(0)+∞，上单调递减．当0a >时，由()0f x '=，得1x a =，10x a ⎛⎫∈ ⎪⎝⎭，时，()0f x '<，()f x 在10a ⎛⎫ ⎪⎝⎭，上单调递减，1x a ⎛⎫∈+∞ ⎪⎝⎭，时，()0f x '>，()f x 在1a ⎛⎫+∞ ⎪⎝⎭，上单调递增．………………………………………………………………（5分） （Ⅱ）证明：要证4222(1)ln 1ln 2ln (2)4n n nn n n n n -+++>∈* ≥，N ， 即证42223(1)ln 1ln 2ln (2)4n n n n n -+++>∈* ≥，N ． 由（Ⅰ）知，当1a =时，()f x 在(01)，上单调递减，在(1)+∞，上单调递增．1()ln 1(1)0f x x f x =+-=≥，∴1ln 1x x -≥，∴221ln 1x x -≥， ∴222222111ln1ln 2ln 11112n n +++-+-++- ≥，∴2221112ln12ln 22ln 12n n n ⎛⎫+++-+++ ⎪⎝⎭ ≥． 又2221111111+++121223(1)n n n +++<+⨯⨯- ， ∴2221111111+++121223(1)n n n n n ⎛⎫⎛⎫-+++>-+ ⎪ ⎪⨯⨯-⎝⎭⎝⎭211111(1)11+++2231n n n n n ⎡⎤-⎛⎫⎛⎫⎛⎫=-+---= ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦ ， ∴2(1)ln1ln 2ln 2n n n -+++> ．………………………………………………………（9分） 由柯西不等式，2222222(ln 1ln 2ln )(111)(ln1ln 2ln )n n +++++++++ ≥． ∴4222231(1)ln 1ln 2ln (ln1ln 2ln )4n n n n n -+++++> ≥+． ∴42223(1)ln 1ln 2ln 4n n n -+++> ， ∴4222(1)ln 1ln 2+ln (2*)4n n nn n n n n -++>∈N ≥，．…………………………………（12分） 22．（本小题满分10分）【选修4−4：坐标系与参数方程】解：（Ⅰ）将参数方程转化为一般方程1(l y k x =：，①21)3l y x k =：，②①×②消k 可得：2213x y +=．即P 的轨迹方程为221(0)3x y y +=≠．1C 的普通方程为221(0)3x y y +=≠．1C的参数方程为sin x y αα⎧=⎪⎨=⎪⎩，，（α为参数πk k α≠∈Z ，）．………………………（5分）（Ⅱ）由曲线2C：πsin 4ρθ⎛⎫+= ⎪⎝⎭得：(sin cos )θθ+=即曲线2C 的直角坐标方程为：80x y +-=，由（Ⅰ）知曲线1C 与直线2C 无公共点，曲线1C上的点sin )Q αα，到直线80x y +-=的距离为d == 所以当πsin 13α⎛⎫+= ⎪⎝⎭时，d的最小值为．………………………………………（10分）23．（本小题满分10分）【选修4−5：不等式选讲】解：（Ⅰ）由题意可得10()130111x x g x x x x x +⎧⎪=-<<⎨⎪--⎩，≤，，，，≥，因为()4g x >-，由图象可得不等式的解为53x -<<，所以不等式的解集为{|53}x x -<<．……………………………………………………（5分） （Ⅱ）因为存在1x ∈R ，也存在2x ∈R ，使得12()()f x g x =成立，所以{|()}{|()}y y f x x y y g x x =∈=∈≠∅R R ，，，又()|2||25||(2)(25)||5|f x x a x x a x a =-++--+=+≥，当且仅当(2)(25)0x a x -+≤时等号成立.由（Ⅰ）知，max ()1g x =，所以|5|1a +≤，解得64a --≤≤，所以实数a 的取值范围为[64]--，．…………………………………………………（10分）。

云南师大附中2018届高考适应性月考（一）理科数学试卷第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，集合，则（）A. B. C. D.【答案】B【解析】因为集合集合，所以，故选B.2. 已知复数，则（）A. 2B.C. 4D.【答案】D【解析】因为，故，故选D.3. 已知平面向量的夹角为，，，则（）A. 2B. 3C. 4D.【答案】D【解析】,,故选D.学,科,网...学,科,网...学,科,网...学,科,网...学,科,网...4. 将函数的图象向左平移个单位，所得的图象所对应的函数解析式是（）A. B. C. D.【答案】C【解析】的图象向左平移单位得到的图象，即将函数的图象向左平移个单位，所得的图象所对应的函数解析式是，故选C.5. 等差数列的前项和为，且，，则（）A. 8B. 9C. 10D. 11【答案】D【解析】因为，又，，故选D.6. 已知点在不等式组，表示的平面区域上运动，则的最大值是（）A. 4B. 3C. 2D. 1【答案】A【解析】画出不等式组，表示的平面区域，如图，平移直线，当直线过点时，直线截距最大，即当时，取得最大值，故选A. 【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.7. 从某社区随机选取5名女士，其身高和体重的数据如下表所示：（（）根据上表可得回归直线方程，据此得出的值为（）A. 43.6B. -43.6C. 33.6D. -33.6【答案】B【解析】由表中数据可得，因为回归直线必过，将代入回归方程，可得得，故选B.8. 若直线（）始终平分圆的周长，则的最小值为（）A. B. C. D.【答案】D【解析】直线平分圆周，则直线过圆心，所以有（当且仅当时取“=”），故选D.9. 函数的零点个数是（）A. 2B. 3C. 4D. 5【答案】C【解析】因为的零点个数就是的图象交点个数，作出的图象如图，由图象知有个交点，所以函数的零点个数是，故选C.10. 已知分别是的三条边及相对三个角，满足，则的形状是（）A. 等腰三角形B. 等边三角形C. 直角三角形D. 等腰直角三角形【答案】B【解析】由正弦定理得：，又，所以有，即，所以是等边三角形，故选B.11. 已知正三棱锥及其正视图如图所示，则其外接球的半径为（）A. B. C. D.【答案】D【解析】由三视图知：三棱锥是底面边长为，高为的正三棱锥，设其外接球的半径为，则有：，解得：，故选D.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响，对简单组合体三视图问题，先看俯视图确定底面的形状，根据正视图和侧视图，确定组合体的形状.12. 定义在上的偶函数，当时，，且在上恒成立，则关于的方程的根的个数叙述正确的是（）A. 有两个B. 有一个C. 没有D. 上述情况都有可能【答案】A【解析】由题意知：在上单调递增，在上恒成立，必有恒成立，，则函数在递增，在递减，且函数在时有最小值，所以的根有个，故选A.【方法点睛】本题主要考查函数的奇偶性、单调性以及不等式恒成立问题，属于难题.对于求不等式恒成立时的参数范围问题，在可能的情况下把参数分离出来，使不等式一端是含有参数的不等式，另一端是一个区间上具体的函数, 这样就把问题转化为一端是函数, 另一端是参数的不等式，便于问题的解决. 但要注意分离参数法不是万能的, 如果分离参数后,得出的函数解析式较为复杂, 性质很难研究, 就不要使用分离参数法.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 展开式中常数项是__________．【答案】495【解析】,解得，代入得常数项为，故答案为.【方法点晴】本题主要考查二项展开式定理的通项与系数，属于简单题. 二项展开式定理的问题也是高考命题热点之一，关于二项式定理的命题方向比较明确，主要从以下几个方面命题：（1）考查二项展开式的通项公式；（可以考查某一项，也可考查某一项的系数）（2）考查各项系数和和各项的二项式系数和；（3）二项展开式定理的应用.14. 执行如图所示的程序框图后，输出的结果是__________．（结果用分数表示）【答案】【解析】该程序执行的是,故答案为.15. 已知双曲线（）的右焦点为，过作轴的垂线，与双曲线在第一象限内的交点为，与双曲线的渐近线在第一象限的交点为，满足，则双曲线离心率的值是__________．【答案】【解析】由已知：，由知：，故答案为.【方法点睛】本题主要考查双曲线的几何性质及离心率，属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点，一般求离心率有以下几种情况：①直接求出，从而求出;②构造的齐次式，求出;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解．16. 设是的三边垂直平分线的交点，是的三边中线的交点，分别为角的对应的边，已知，则的取值范围是__________．【答案】【解析】，又，代入得，又，所以，代入得的取值范围为，故答案为.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知数列满足，（）.（1）求证：数列是等比数列；（2）若满足，求数列的前项和.【答案】(1)见解析;（2）.【解析】试题分析：（1）由题意得，即证证数列是以等比数列；（2）由（1）可求即，结合数列的特点，故利用错位相减求和即可.试题解析：（Ⅰ）证明：因为，所以，而，故数列是首项为4，公比为2的等比数列．（Ⅱ）解：由（Ⅰ）得数列是首项为4，公比为2的等比数列，即，因此．所以，，①，②−②有，所以．【易错点晴】本题主要考查等差数列的定义、“错位相减法”求数列的和，属于中档题. “错位相减法”求数列的和是重点也是难点，利用“错位相减法”求数列的和应注意以下几点：①掌握运用“错位相减法”求数列的和的条件（一个等差数列与一个等比数列的积）；②相减时注意最后一项的符号；③求和时注意项数别出错；④最后结果一定不能忘记等式两边同时除以.18. 某班级体育课举行了一次“投篮比赛”活动，为了了解本次投篮比赛学生总体情况，从中抽取了甲乙两个小组样本分数的茎叶图如图所示.甲乙（1）分别求出甲乙两个小组成绩的平均数与方差，并判断哪一个小组的成绩更稳定：（２）从甲组成绩不低于60分的同学中，任意抽取3名同学，设表示所抽取的3名同学中得分在的学生个数，求的分布列及其数学期望.【答案】(1)甲乙平均数均为68，方差分别为103，45; 乙组的成绩更稳定；（2）的分布列为：0 1 2 3P.【解析】试题分析：（1）算出甲乙两个小组成绩的平均数与方差，可得甲乙平均数均为68，方差分别为103，45，可得乙组的成绩更稳定；（2）的取值可能为：0，1，2，3，分别算出各随机变量对应的概率即可得分布列，利用期望公式可得结果.试题解析：（1），，，，所以乙组的成绩更稳定．（2）由题意知服从参数为3，3，7的超几何分布，即，的取值可能为：0，1，2，3，，，，，的分布列为：0 1 2 3P的数学期望：．19. 如图，在长方体中，与平面及平面所成角分别为，，分别为与的中点，且.（1）求证：平面；（2）求二面角的平面角的正弦值.【答案】(1)见解析;（2）.【解析】试题分析：（1）根据中位线定理可得MN∥CD，由长方体的性质可得CD⊥平面，从而可得结果；（2）以AB，AD，所在直线为x，y，z轴建立空间直角坐标系，分别求出平面与平面的的一个法向量，根据空间向量夹角余弦公式及同角三角函数之间的关系，可得结果.试题解析：（1）证明：在长方体中，因为，所以为的中位线，所以MN∥CD，又因为CD⊥平面，所以MN⊥平面．（2）解：在长方体中，因为CD⊥平面，所以为与平面所成的角，即=，又因为⊥平面，所以为与平面所成的角，即，所以，，，=，，如图2，分别以AB，AD，所在直线为x，y，z轴建立空间直角坐标系，∴A(0，0，0)，D(0，2，0)，，，C(2，2，0)，B(2，0，0)，在正方形ABCD中，BD⊥AC，∴是平面的法向量，.设平面的法向量为，由，，所以有∴取z=1，得平面的一个法向量为.设二面角的大小为，则.∴．【方法点晴】本题主要考查线面垂直的判定、利用空间向量求二面角，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.20. 已知椭圆（）的两个顶点分别为，，点为椭圆上异于的点，设直线的斜率为，直线的斜率为，.（1）求椭圆的离心率；（2）若，设直线与轴交于点，与椭圆交于两点，求的面积的最大值.【答案】(1);（2）面积的最大值为.【解析】试题分析：（1）可得，，所以，从而可得结果；（2）设直线的方程为：代入椭圆的方程有：，根据韦达定理，弦长公式即三角形面积公式可得，利用基本不等式可得结果.试题解析：（1），整理得：，又，，所以，．（2）由（Ⅰ）知，又，所以椭圆C的方程为.设直线的方程为：代入椭圆的方程有：，设，，令，则有，代入上式有，当且仅当即时等号成立，所以的面积的最大值为．21. 设函数（1）若函数在上单调递增，求的取值范围；（2）求证：当时，【答案】(1);（2）见解析.【解析】试题分析：（1）求出，讨论两种情况：，，分别令得增区间，令是其子集即可得结果；（2）由（1）知，当时，在上单调递增，由可得，化简即可得结果.试题解析：（1）解：，当时，在上恒成立，所以在上单调递增成立，当时，由，解得，易知，在上单调递减，在上单调递增，由题意有，，解得．综上所述，．（2）证明：由（1）知，当时，在上单调递增，对任意，有成立，所以，代入有，整理得：.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. 选修4-4：坐标系与参数方程已知曲线的参数方程为：（为参数），直线的参数方程为：（为参数），点，直线与曲线交于两点.（1）分别写出曲线在直角坐标系下的标准方程和直线在直角坐标系下的一般方程；（2）求的值.【答案】(1);（2）.【解析】试题分析：（1）利用平方法消去参数可得曲线在直角坐标系下的标准方程，利用代入法消去参数可得线在直角坐标系下的一般方程；（2）将直线的参数方程化为标准方程：代入椭圆方程，利用直线参数方程的几何意义及韦达定理可得结果.试题解析：（1）曲线C的标准方程为：，直线的一般方程为：．（2）将直线的参数方程化为标准方程：代入椭圆方程得：，解得，所以．23. 选修4-5：不等式选讲已知函数.（1）请写出函数在每段区间上的解析式，并在图中的直角坐标系中作出函数的图象；（2）若不等式对任意的实数恒成立，求实数的取值范围.【答案】(1)见解析;（2）.【解析】试题分析：（1）描点法可画出函数图象；（2）的最小值是，要使不等式恒成立，只需，解不等式可得结果.试题解析：（1）函数的图象如图所示．（2）由（1）知的最小值是，所以要使不等式恒成立，有，解之得．。

云南师大附中2018届高考适应性月考卷（七）语文参考答案1．（3分）B【解析】A项曲解文意，出处见第一段：“我国文化繁荣兴盛，国家文化软实力明显提高”，文化泛娱乐现象也随之出现。

C项张冠李戴，出处见第二段，“很多娱乐节目盲目博取点击率”是“文化泛娱乐化背后的动力”，而不是受众广泛的原因。

D项于文无依据。

2．（3分）B【解析】B项无中生有，文章第二段并没有指出文化泛娱乐现象的具体危害。

3．（3分）D【解析】D项张冠李戴。

“传播好真善美”应该是文化生产者的责任。

4．（3分）A【解析】A项分析不准确，“迅速瞄瞄”、“快走几步猫下腰”体现的是在饥荒时期素玉不想让其他人发现高粱穗的警惕心理；“轻轻放进筐里”表现出的是素玉对高粱穗的珍视。

5．（5分）①因为接连几个秋天，素玉都没有捡到一穗高粱，出于内心对粮食的渴望，所以会经常想起曾经捡到过的那穗高粱。

（2分）②素玉想到高粱满怀幸福是因为在最缺粮的时候，那穗高粱让她和孩子得以充饥，度过了那段艰难的日子，对那穗高粱充满了感恩。

（2分）③素玉想到当时几个孩子都给她递过来了半匙米粒，她感受到了孩子们对她的爱，感受到了亲情的暖意，所以回想起来满怀幸福。

（1分）6．（6分）①在环境方面，通过对素玉捡粮食场景的描写，展现了当时农村人民正在闹饥荒的社会环境，写出了农村生活的艰苦。

②在情节方面，小说以素玉认真仔细捡粮食开头，为下文素玉捡到高粱穗作了铺垫。

③在人物形象塑造方面，突出了素玉的勤劳、能干以及在恶劣环境中生存的智慧。

（每点2分）7．（3分）A【解析】增长量最大的是2013年。

今年上网人数—去年的上网人数=今年的增长量；本题学生应根据所给数据先算出2011年的上网人数，然后才能得出2012年的增长量。

8．（5分）D（3分）E（2分）【解析】A．因果倒置；B．说法绝对，商家要想获得贷款，需要满足信用要求，不是随便就可以贷款；C．材料三“以二维码为代表的‘条码支付’”说明“二维码”只是“条码”中的其中一种。

云南师大附中2018届高考适应性月考卷（七）语文参考答案1．（3分）B 【解析】A项歪曲文意，出处见第一段：“我国文化繁荣兴盛，国家文化软实力明显提高”，文化泛娱乐现象也随之显现。

C项张冠李戴，出处见第二段，“很多娱乐节目盲目博取点击率”是“文化泛娱乐化背后的动力”，而不是受众普遍的缘故。

D项于文无依据。

2．（3分）B 【解析】B项无中生有，文章第二段并无指出文化泛娱乐现象的具体危害。

3．（3分）D 【解析】D项张冠李戴。

“传播好真善美”应该是文化生产者的责任。

4．（3分）A 【解析】A项分析不准确，“迅速瞄瞄”、“快走几步猫下腰”表现的是在饥荒时期素玉不想让其他人发觉高粱穗的警戒心理；“轻轻放进筐里”表现出的是素玉对高粱穗的珍视。

5．（5分）①因为接连几个秋季，素玉都没有捡到一穗高粱，出于内心对粮食的期望，因此会常常想起曾经捡到过的那穗高粱。

（2分）②素玉想到高粱满怀幸福是因为在最缺粮的时候，那穗高粱让她和小孩得以果腹，度过了那段艰巨的日子，对那穗高粱充满了感恩。

（2分）③素玉想到那时几个小孩都给她递过来了半匙米粒，她感受到了小孩们对她的爱，感受到了亲情的暖意，因此回忆起来满怀幸福。

（1分）6．（6分）①在环境方面，通过对素玉捡粮食场景的描述，展现了那时农村人民正在闹饥荒的社会环境，写出了农村生活的艰苦。

②在情节方面，小说以素玉认真认真捡粮食开头，为下文素玉捡到高粱穗作了铺垫。

③在人物形象塑造方面，突出了素玉的勤劳、能干和在恶劣环境中生存的聪慧。

（每点2分）7．（3分）A 【解析】增加量最大的是2021年。

今年上网人数—去年的上网人数=今年的增长量；此题学生应依照所给数据先算出2020年的上网人数，然后才能得出2021年的增长量。

8．（5分）D（3分）E（2分）【解析】A．因果倒置；B．说法绝对，商家要想取得贷款，需要知足信誉要求，不是随意就能够够贷款；C．材料三“以二维码为代表的‘条码支付’”说明“二维码”只是“条码”中的其中一种。

云南师大附中2018届高考适应性月考卷（三）语文参考答案1．（3分）B【解析】A．曲解文意，此语言教学法的核心是“以明确任务为前提完成语言交际”。

C．以偏概全，这只是其中一种分类方式。

D．“直接引入”表述不当，还加入“驱动”一词，说明国内学者并非完全照搬。

2．（3分）A【解析】“历史沿革”指某事物发展和变化的历程。

本文只论述了这一概念产生的理论渊源。

3．（3分）D【解析】“避免套作、宿构”说法绝对，对传统作文材料的理解错误。

4．（3分）B【解析】“人情冷暖、世态炎凉”说法不准确，应是“可见作者情感的压抑与封闭”。

5．（5分）①内容意蕴上，以歌词和节奏来喻指普通人物的平凡生活和故事情节的简洁单调。

②情节组织上，起贯穿全文的线索作用。

文章开篇以“歌”来浓缩对老屋的回忆，奠定情感基调；中间以对“歌”的怀想来品评这段往事的意蕴；结尾呼应开头，以“歌声”的回环往复来体现情节的完整性，凸显怀旧的意味。

③人物刻画上，表现作者情感的冷峻、克制与压抑。

④思想主旨上，表达作者对生命的感悟：正因为有梦，单调的生活变得复杂，窄小的心灵变得广阔，充满苦难与绝望的现实变得有期望。

（评分标准：①②③每点1分，第④点2分）6．（6分）①“经验自我”是23岁时的“我”，用于对情节的叙述，写出年轻时的“我”的所见所闻所感，拉近“我”与读者之间的距离；②“叙述自我”是现在的“我”，用于对过往人和事的评述，写出“我”的所思所想所悟，推远“我”的故事与读者之间的距离；③两个“我”同时在场，让读者既感受主人公的心灵体验，又体会人生的哲理思考，在感性和理性之间极大丰富作品的审美内涵。

（每点2分）7．（3分）C【解析】这是“以前普遍认为”的观点，而非本文观点。

8．（5分）A（3分）E（2分）【解析】B．转移支付非必要条件。

C．说法绝对，以偏概全。

D．文中无据。

9．（4分）①加大中央财政转移支付力度，通过转移支付增加低收入阶层收入。

②进一步加大收入分配机制改革力度，完善税收政策，尽量缓解贫富分化现象。

2018届云南省师大附中高考适应性月考理科数学试卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合1{()1}3xA x =≤，2{230}B x x x =--≥，则AB =（ ）A ．{0}x x ≥B ．{1}x x ≤-C ．{3}x x ≥D ．{31}x x x ≥≤-或 2.设复数z 满足(1)12i z i +=-，则复数z 对应的点位于复平面内（ ） A ．第一象限 B ．第二象限 C ． 第三象限 D ．第四象限3.命题:p x R ∀∈，20x ax a ++≥，若命题p 为真命题，则实数a 的取值范围是（ ） A ．(0,4) B ．[0,4] C ．(,0)(4,)-∞+∞ D ．(,0][4,)-∞+∞4.执行如图所示的程序框图，则输出的结果是（ ）A ．4B ．-4 C.5 D ．-55.已知直线l 的倾斜角为23π，直线1l 经过(3)P -，(,0)Q m 两点，且直线l 与1l 垂直，则实数m 的值为（ ）A ．-2B ．-3 C. -4 D ．-56.若621()ax x +的展开式中常数项为1516，则实数a 的值为（ ） A ．2± B ．12 C.-2 D ．12±7.将函数()2cos()4f x x πω=+（0ω>）的图象向右平移4πω个单位，得取函数()y g x =的图象，若()y g x =在[0,]3π上为减函数，则ω的最大值为（ ）A ．2B ． 3 C. 4 D ．58.已知某空间几何体的三视图如图所示，则该几何体的表面积是（ ）A ．122226+．12226+ C. 12226+ D ．1226+ 9.已知三棱锥P ABC -的所有顶点都在球O 的球面上，PA AB ⊥，PA AC ⊥，060BAC ∠=，2PA =，2AB =，3AC =，则球O 的表面积为（ ）A ．403π B ．303π C. 203π D ．103π 10.点P 在椭圆22221(0)x y a b a b+=>>上，12,F F 是椭圆的两个焦点，01260F PF ∠=，且12F PF ∆的三条边2||PF ，1||PF ，12||F F 成等差数列，则此椭圆的离心率是（ ） A ．45 B ．34 C. 23 D ．1211.已知函数()2ln f x ax x x =+，32()21g x x x =--，如果对于任意的1,[,2]2m n ∈，都有()()f m g n ≥成立，则实数a 的取值范围为（ ）A ．[1,)-+∞B ．(1,)-+∞ C. 1[,)2-+∞ D ．1(,)2-+∞12.已知圆O 的半径为2，,P Q 是圆O 上任意两点，且060POQ ∠=，AB 是圆O 的一条直径，若点C 满足(1)OC OP OQ λλ=-+（R λ∈），则CA CB •的最小值为（ ） A ．-1 B ．-2 C.-3 D ．-4二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若实数,x y 满足不等式组2010220x x y x y -≤⎧⎪-+≥⎨⎪++≥⎩，则23z x y =+的最小值为 ．14.设数列{}n a 的前n 项和为n S ，且11a =，131n n a S +=+，则4S = ． 15.已知平面区域11{(,)}1x D x y y ⎧≤⎪=⎨≤⎪⎩，1221(1)D x dx -=-⎰，在区域1D 内随机选取一点M ，则点M 恰好取自区域2D 的概率是 ．16.已知函数23,30()ln(1),03x x x f x x x ⎧-+-≤≤=⎨+<≤⎩，若()()33g x f x ax a =--有三个零点，则实数a 的取值范围是 ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 在ABC ∆中，,,a b c 分别是角,,A B C 的对边，(2)cos cos 0b c A a C --=. （1）求角A 的大小；（2）若2a =，求ABC ∆的面积S 的最大值.18. 为考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校高中生中，从男生中随机抽取了70人，从女生中随机抽取了50人，男生中喜欢数学课程的占47，女生中喜欢数学课程的占710，得到如下列联表.（1）请将列联表补充完整；试判断能否有90%的把握认为喜欢数学课程与否与性别有关；（2）从不喜欢数学课程的学生中采用分层抽样的方法，随机抽取6人，现从6人中随机抽取2人，若所选2名学生中的女生人数为X ，求X 的分布列及数学期望.附：22()()()()()n ad bc k a b c d a c b d -=++++，其中n a b c d =+++.0k2.072 2.7063.841 5.024 6.635 7.879 10.82819. 如图，四棱锥P ABCD -的底面ABCD 是平行四边形，PA ⊥底面ABCD ，3PA =，2AD =，4AB =，060ABC ∠=.（1）求证：平面PBC ⊥平面PAC ； （2）E 是侧棱PB 上一点，记PEPBλ=（01λ<<），是否存在实数λ，使平面ADE 与平面PAD 所成的二面角为060若存在，求出λ的值；若不存在，请说明理由. 20. 已知函数1()ln1f x a x x=++. （1）求函数()f x 的单调区间和极值；（2）是否存在实数a ，使得函数()f x 在[1,]e 上的最小值为1？若存在，求出a 的值；若不存在，请说明理由.21. 已知点A 为圆228x y +=上一动点，AN x ⊥轴于点N ，若动点Q 满足(1)OQ mOA m ON =+-（其中m 为非零常数）（1）求动点Q 的轨迹方程；（2）若Γ是一个中心在原点，顶点在坐标轴上且面积为8的正方形，当22m =时，得到动点Q 的轨迹为曲线C ，过点(4,0)P -的直线l 与曲线C 相交于,E F 两点，当线段EF 的中点落在正方形Γ内（包括边界）时，求直线l 斜率的取值范围.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在平面直角坐标系xOy 中，已知直线l 经过点1(1,)2P ，倾斜角3πα=，在以原点O 为极点，x 轴的正半轴为极轴的极坐标系中，曲线C 的极坐标方程为ρ=（1）写出直线l 的参数方程，并把曲线C 的极坐标方程化为直角坐标方程； （2）设l 与曲线C 相交于,A B 两点，求PA PB •的值. 23.选修4-5：不等式选讲 设函数()221f x x x =--+. （1）解不等式()0f x ≤；（2）若对于x R ∀∈，使2()24f x m m -≤恒成立，求实数m 的取值范围.2018届云南省师大附中高考适应性月考卷数学（理）参考答案一、选择题（本大题共12小题，每小题5分，共60分）题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CBBADDBAADCC【解析】1．{|0}{|31}A x x B x x x ==-≥，≥或≤，∴{|3}A B x x =≥，故选C ．2．12i 13i 1i 22z -==--+，13i 22z =-+，故选B ．3．对于20x x ax a ∀∈++R ，≥成立是真命题，∴240a a ∆=-≤，即04a ≤≤，故选B ． 4．由题意可知输出结果为123484S =-+-+-⋅⋅⋅+=，故选A ． 5．∵130312l l k k m-=-=---，∴5m =-，故选D ．6．621ax x ⎛⎫+ ⎪⎝⎭的展开式通项为666316621C ()C rr r r r r r T ax a x x ---+⎛⎫== ⎪⎝⎭，令630r -=，则有2r =，∴24615C 16a =，即4116a =，解得12a =±，故选D ． 7．由题意可得函数()g x 的解析式为ππ()2cos 2cos 44g x x x ωωω⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦，函数()g x 的一个单调递减区间是π0ω⎡⎤⎢⎥⎣⎦，，若函数()y g x =在区间π03⎡⎤⎢⎥⎣⎦，上为减函数，则ππ003ω⎡⎤⎡⎤⊆⎢⎥⎢⎥⎣⎦⎣⎦，，，只要ππ3ω≥，∴3ω≤，则ω的最大值为3，故选B ．8．由三视图知：几何体为四棱锥，且四棱锥的一条侧棱与底面垂直，如图1，PA ⊥平面ABCD ，2PA =，2AB =，4AD =，2BC =，经计算，25PD =，23PC =，22DC =，∴PC CD ⊥，∴12222PAB S =⨯⨯=△，12442PAD S =⨯⨯=△，1222222PBC S =⨯⨯=△，12223262PCD S =⨯⨯=△，1(24)262ABCD S =⨯+⨯=，∴122226S =++表，故选A ．9．设ABC △外接圆半径为r ，三棱锥外接球半径为R ，∵2360AB AC BAC ==∠=︒，，，∴2222212cos602322372BC AB AC AB AC =+-︒=+-⨯⨯⨯=，∴BC 2sin60BCr ==︒，∴r =，由题意知，PA ⊥平面ABC ，则将三棱锥补成三棱柱可得，22221101293PA R r ⎛⎫=+=+= ⎪⎝⎭，∴210404π4ππ33S R ==⨯=，故选A ． 10．设1122||||PF r PF r ==，，由椭圆的定义得：122r r a +=，∵12F PF △的三条边2PF ||，112||||PF F F ，成等差数列，∴1222r c r =+，联立122r r a +=，1222r c r =+，解得 12224233a c a cr r +-==，，由余弦定理得：2221212(2)2cos60c r r r r =+-︒，将12224233a c a cr r +-==，代入2221212(2)2cos60c r r r r =+-︒可得，222243a c c +⎛⎫=+ ⎪⎝⎭2422242123332a c a c a c -+-⎛⎫- ⎪⎝⎭，整理得：2220c ac a +-=，由c e a =，得2210e e +-=，解得：12e =或1e =-（舍去），故选D ． 11．对于任意的122m n ⎡⎤∈⎢⎥⎣⎦，，，都有()()f m g n ≥成立，等价于在122⎡⎤⎢⎥⎣⎦，，函数min max ()()f x g x ≥，24()3433g x x x x x ⎛⎫'=-=- ⎪⎝⎭，()g x 在1423⎡⎤⎢⎥⎣⎦，上单调递减，在423⎛⎤⎥⎝⎦，上单调递增，且111(2)182g g ⎛⎫-=<=- ⎪⎝⎭，∴max ()(2)1g x g ==-．在122⎡⎤⎢⎥⎣⎦，上，()2ln 1f x ax x x =+-≥恒成立，等价于ln 112ln x x a x x x --=--≥恒成立．设1()ln h x x x =--，22111()x h x x x x -'=-+=，()h x 在112⎡⎤⎢⎥⎣⎦，上单调递增，在(12]，上单调递减，所以max ()(1)1h x h ==-，所以12a -≥，故选C ．12．因为2()()()CA CB CO OA CO OB CO CO OA OB OA OB =++=+++，由于圆O 的半径为2，AB 是圆O 的一条直径，所以0OA OB +=，22(1)4OA OB =⨯⨯-=-，又60POQ ∠=︒，所以22224[(1)]4(1)2(1)CA CB CO OP OQ OP OP OQ λλλλλ=-=-+-=-+- 224OQ λ+-224(331)44(33)λλλλ=-+-=-2134324λ⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，所以，当12λ=时，2min1333244λ⎡⎤⎛⎫--=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，故CA CB 的最小值为3434⎛⎫⨯-=- ⎪⎝⎭，故选C ．二、填空题（本大题共4小题，每小题5分，共20分）题号 13 14 15 16 答案14-8513ln 2163e ⎡⎫⎪⎢⎣⎭，【解析】13．画出不等式组表示的可行域知，23z x y =+的最小值为14-．14．131n n a S +=+①，131(2)n n a S n -=+≥②，①-②得：14(2)n n a a n +=≥，又1211314a a a ==+=，， ∴数列{}n a 首项为1，公比为4的等比数列，∴414166485S =+++=．15．依题意知，平面区域1D 是一个边长为2的正方形区域（包括边界），其面积为4， 112321114(1)d 33D x x x x --⎛⎫=-=-= ⎪⎝⎭⎰，如图2，点M 恰好取自区域2D 的概率41343P ==．16．由()|()|330g x f x ax a =--=，得|()|333(1)f x ax a a x =+=+，设3(1)y a x =+，则直线过定点(10)-， 作出函数|()|f x 的图象（图象省略）．两函数图象有三个交点. 当30a ≤时，不满足条件；当30a >时，当直线3(1)y a x =+经过点(3ln 4)，时，此时两函数图象有3个交点，此时ln 434a =，ln 26a =；当直线3(1)y a x =+与ln(1)y x =+相切时，有两个交点，此时函数的导数1()1f x x '=+，设切点坐标为()m n ，，则ln(1)n m =+，切线的斜率为1()1f m m '=+，则切线方程为1ln(1)()1y m x m m -+=-+，即1ln(1)11m y x m m m =-++++，∵131a m =+且3ln(1)1m a m m =-+++，∴1ln(1)11m m m m =-++++，即1ln(1)111m m m m +=+=++，则1e m +=，即e 1m =-，则1131e a m ==+，∴13ea =，∴要使两个函数图象有3个交点，则ln 2163ea <≤． 三、解答题（共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分）解：（Ⅰ）因为(2)cos cos 0b c A a C --=， 所以2cos cos cos 0b A c A a C --=，由正弦定理得2sin cos sin cos sin cos 0B A C A A C --=， 即2sin cos sin()0B A A C -+=，又πA C B +=-，所以sin()sin A C B +=， 所以sin (2cos 1)0B A -=，在ABC △中，sin 0B ≠，所以2cos 10A -=，所以π3A =． （Ⅱ）由余弦定理得：222222cos a b c bc A b c bc =+-=+-， ∴42bc bc bc -=≥，∴1sin 42S bc A ===，当且仅当b c =时“=”成立，此时ABC △为等边三角形， ∴ABC △的面积S18．（本小题满分12分） 解：（Ⅰ）22⨯列联表补充如下：由题意得2120(40153035) 2.0577*******K ⨯⨯-⨯=≈⨯⨯⨯，∵2.057 2.706<，∴没有90%的把握认为喜欢数学课程与否与性别有关．） （Ⅱ）用分层抽样的方法抽取时，抽取比例是624515=， 则抽取男生230415⨯=人，抽取女生215215⨯=人， 所以X 的分布列服从参数622N M n ===，，的超几何分布，X 的所有可能取值为012，，，其中22426C C ()(012)C i iP X i i -===，，． 由公式可得022426C C 6(0)C 15P X ===，112426C C8(1)C 15P X ===，202426C C 1(2)C 15P X ===， 所以X 的分布列为：所以X 的数学期望为6812()0121515153E X =⨯+⨯+⨯=． 19．（本小题满分12分）（Ⅰ）证明：由已知，得AC == ∵2BC AD ==，4AB =，又222BC AC AB +=，∴BC AC ⊥． 又PA ⊥底面ABCD ，BC ⊂平面ABCD ， 则PA BC ⊥，∵PA ⊂平面PAC ，AC ⊂平面PAC ，且PA AC A =，∴BC ⊥平面PAC ．∵BC ⊂平面PBC ，∴平面PBC ⊥平面PAC ．（Ⅱ）解：以A 为坐标原点，过点A 作垂直于AB 的直线为x 轴，AB AP ，所在直线分别为y 轴，z 轴建立空间直角坐标系A xyz -，如图3所示． 则(000)(040)(003)A B P ，，，，，，，，，因为在平行四边形ABCD 中，2460AD AB ABC ==∠=︒，，， 则30DAx ∠=︒，∴10)D -，． 又(01)PEPBλλ=<<，知(043(1))E λλ-，，． 设平面ADE 的法向量为111()m x y z =，，， 则00m AD m AE ⎧=⎪⎨=⎪⎩，，即1111043(1)0y y z λλ-=+-=⎪⎩，，取11x =，则1m ⎛= ⎝⎭，． 设平面PAD 的法向量为222()n x y z =，，， 则00n AP n AD ⎧=⎪⎨=⎪⎩，，即222300z y =⎧⎪-=，， 取21y =，则3103n ⎛⎫= ⎪ ⎪⎝⎭，，． 若平面ADE 与平面PAD 所成的二面角为60︒，则1cos cos602mn 〈〉=︒=，11012113++=+，化简得224123(1)λλ+=-，即2914λλ⎛⎫= ⎪-⎝⎭， 解得3λ=（舍去）或35λ=． 于是，存在35λ=，使平面ADE 与平面PAD 所成的二面角为60︒．20．（本小题满分12分）解：由题意知函数的定义域为{|0}x x >，()1a x a f x x x-'=-+=． （Ⅰ）①当0a ≤时，()0f x '>，所以函数()f x 的单调递增区间是(0)+∞，，无极值； ②当0a >时，由()0f x '>，解得x a >，所以函数()f x 的单调递增区间是()a +∞，， 由()0f x '<，解得x a <，所以函数()f x 的单调递减区间是(0)a ，． 所以当x a =时，函数()f x 有极小值()ln 1f a a a a =-++． （Ⅱ）由（Ⅰ）可知，①当1a ≤时，函数()f x 在[1e]，为增函数， ∴函数()f x 在[1e]，上的最小值为(1)ln1112f a =++=，显然21≠，故不满足条件； ②当1e a <≤时，函数()f x 在[1)a ，上为减函数，在[e]a ，上为增函数， 故函数()f x 在[1e]，上的最小值为()f x 的极小值()ln 1=1f a a a a =-++，即e a =，满足条件； ③当e a >时，函数()f x 在[1e]，为减函数，故函数()f x 在[1e]，上的最小值为1(e)ln e 11ef a =++=，即e a =，不满足条件． 综上所述，存在实数e a =，使得函数()f x 在[1e]，上的最小值为1．21．（本小题满分12分）解：（Ⅰ）设动点00()()Q x y A x y ，，，，则0(0)N x ，，且22008x y +=，① 又(1)OQ mOA m ON =+-，得001x x y y m==，， 代入①得动点Q 的轨迹方程为222188x y m+=． （Ⅱ）当2m =时，动点Q 的轨迹曲线C 为22184x y +=． 直线l 的斜率存在，设为k ，则直线l 的方程为(4)y k x =+，代入22184x y +=，得2222(12)163280k x k x k +++-=，由2222(16)4(12)(328)0k k k ∆=-+->，解得k << 设1122()()E x y F x y ，，，，线段EF 的中点()G x y ''，， 则2122284(4)21212x x k k x y k x k k +'''==-=+=++，． 由题设知，正方形Γ在y 轴左边的两边所在的直线方程分别为22y x y x =+=--，，注意到点G 不可能在y 轴右侧，则点G 在正方形Γ内（包括边界）的条件是22y x y x ''+⎧⎨''--⎩≤，≥，即22222248212124821212k k k k k k k k ⎧-+⎪⎪++⎨⎪-⎪++⎩≤，≥，解得k 于是直线l的斜率的取值范围为⎡⎢⎣⎦． 22．（本小题满分10分）【选修4−4：坐标系与参数方程】解：（Ⅰ）直线l的参数方程为：112()12x t t y ⎧=+⎪⎪⎨⎪=⎪⎩，为参数，，曲线C 的直角坐标方程为：2213x y +=． （Ⅱ）把直线l的参数方程11212x t y ⎧=+⎪⎪⎨⎪=⎪⎩，，代入曲线C 的方程2213x y +=中，得221113322t ⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭，即2104)50t t +-=， 设点A B ，所对应的参数分别为12t t ，，则1212t t =-，∴121211||||||||||22PA PB t t t t ===-=． 23．（本小题满分10分）【选修4−5：不等式选讲】 解：（Ⅰ）不等式()0f x ≤，即|2||21|x x -+≤，即2244441x x x x -+++≤，23830x x +-≥，解得133x x -≥或≤， 所以不等式()0f x ≤的解集为133x x x ⎧⎫-⎨⎬⎩⎭≥或≤. （Ⅱ）1321()|2||21|312232x x f x x x x x x x ⎧+<-⎪⎪⎪=--+=-+-⎨⎪-->⎪⎪⎩，，，≤≤，，， 故()f x 的最大值为1522f ⎛⎫-= ⎪⎝⎭， 因为对于x ∀∈R ，使2()24f x m m -≤恒成立， 所以25242m m +≥，即24850m m +-≥， 解得1522m m -≥或≤，∴5122m ⎛⎤⎡⎫∈-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭，，．。