求曲边梯形的面积详解

格式：ppt
大小：1.80 MB
文档页数：26

下载文档原格式

1.5定积分的概念(高中数学人教A版选修2-2)

C．f
D．f(0)

i－ 1 i 解析：当n很大时，f(x)＝x2在区间 n ，n 上的值可用该区
间上任何一点的函数值近似代替，显然可以用左端点或右端点的函数值近似代替．答案：C
3n －2n 3．linm ＝________. 2 →∞ n
分析：按照“分割→近似代替→求和→取极限”的步骤进行．
解析：(1)分割．
3 1,2，…，n)的长度为Δx＝ n .分别过各分点作x轴的垂线，把原
3i－1 3i 如上图，将区间[0,3]n等分，则每个区间 (i＝， n n
曲边梯形分成n个小曲边梯形．
(2)近似代替．以每个小区间的左端点函数值为高作n个小矩形．则当n
(4)取极限． S＝lim S n→∞ n ＝lim n→∞
1 1 1 1 － 1 － 1 －－ 9 ＋ 9 ＋ 9 n 2n n
＝－9(1－0)(1－0)＋9(1－0)＋9＝9，即所求曲边梯形面积为S＝9.
i－ 1
上，随着n的增大，f(x)的值的变化逐渐缩小，当n很大时，f(x)的值变化很小．答案：D
解析：函数f(x)＝x2在区间
i ， n n
i－1 i 2．当n很大时，函数f(x)＝x2在区间 n ，n

上的值可以用下
列哪个值近似代替(
)
2 B．f
3n2－2n 2 3 －解析： linm ＝ lim ＝3. 2 →∞ n→∞ n n 答案：3
2
求解曲边梯形的面积是用“以直代曲”和逼近的思想方法；其步骤为：①分割；②近似代替；③求和；④取极限．
导数及其应用

曲边梯形的面积完整版

a,b叫做积分区间,函数f x叫做被积函数, x叫
做积分变量, f x dx叫做被积式.
知识归纳
1.定积分的概念: 函数f(x)在区间[a, b]上的定积分,记作:
b
a f ( x)dx
b
n1
f (x)dx
a
f (i )
i0
xi
n
lim n i1
(b a) n
f (i )
2.定积分的几何意义:
• 在 [a, b]中任意插入 n -1个分点．
• 得n个小区间： [xi1 , xi ] (i=1, 2 , ···, n)．
• 区间[xi1 , xi ]的长度xi xi xi1 ．
y
f(2) f(1)
• 把曲边梯形分成 n 个窄曲边梯形．
y = f(x) f(i)
f(i)xi
O a 1 x1 2 x2
n nn
nn
nn
每个区间的长度为 x i i 1 1 nn n
过各区间端点作x轴的垂线，从而得到n 个小曲边梯形，他们的面积分别记作
S1, S2,, Si ,, Sn.
(2) 以直代曲
Si
f(i
1)x n
(i
1)2 n
1 n
(3) 作和
n
S S1 S2 Sn Si i1
• 于是得到弹簧从平衡位置拉长b所做的功为：
• [点拨] 按用定义求定积分的步骤即分割、近似代替、求和、取极限求解．
y=f(x)所围成的曲边梯形的面积(因而定积
分是一个确定的常数) y
3.定积分的作用 f (b)
f (a)
求曲边梯形的面积
0a
y f (x)
b

简述求曲边梯形面积的方法步骤

简述求曲边梯形面积的方法步骤求解曲边梯形面积是数学中的一个基本问题，它涉及到了多种数学知识和技巧。

在这里，我们将为大家详细介绍如何求解曲边梯形面积。

一、什么是曲边梯形？曲边梯形是指四边形中有两条平行线段且相邻两侧的线段长度不等的四边形。

其中，一条平行线段称为上底，另一条平行线段称为下底，相邻两侧的线段分别称为斜边或侧面。

二、求解曲边梯形面积的方法1. 通过公式计算当我们已知曲边梯形的上底长a、下底长b和高h时，可以通过以下公式来计算其面积：S = (a + b) × h ÷ 2其中，S表示曲边梯形的面积。

2. 分割成矩形和三角形当我们无法直接计算出曲边梯形的面积时，可以将其分割成矩形和三角形进行计算。

具体步骤如下：（1）将曲边梯形沿着高分成两个三角形和一个矩形；（2）根据三角形的面积公式计算两个三角形的面积；（3）矩形的面积等于上底和下底之和的一半乘以高；（4）将两个三角形的面积和矩形的面积相加，即可得到曲边梯形的面积。

3. 用相似三角形求解当我们已知曲边梯形上底长a、下底长b、高h和斜边长度l时，可以通过以下步骤来计算其面积：（1）将曲边梯形分割成一个小梯形和一个直角三角形；（2）利用相似三角形的性质，可以得到以下公式：h / l = (h - x) / a = x / b，其中x为小梯形上底长；（3）根据以上公式解出x和h - x的值；（4）根据小梯形和直角三角形的面积公式计算出它们各自的面积；（5）将小梯形和直角三角形的面积相加，即可得到曲边梯形的面积。

4. 利用勾股定理求解当我们已知曲边梯形上底长a、下底长b、高h和斜边长度l时，可以通过以下步骤来计算其面积：（1）将曲边梯形分割成一个小梯形和一个直角三角形；（2）利用勾股定理，可以得到以下公式：h² = x² + l²，其中x为小梯形上底长；（3）根据以上公式解出x的值；（4）根据小梯形和直角三角形的面积公式计算出它们各自的面积；（5）将小梯形和直角三角形的面积相加，即可得到曲边梯形的面积。

曲边梯形的面积

y = f(x) y
A1
Ai
An
Oa
bx
将曲边梯形分成 n个小曲边梯形，并用小矩阵形的面积代替
小曲边梯形的面积，于是曲边梯形的面积A近似为
A A1+ A2 + + An
—— 以直代曲,无限逼近
2．曲边梯形的面积
求曲边梯形的面积即
求 y f (x) 下的面积 f (x) 0
若“梯形” 很窄，可近似地用矩形面积代替在不很窄时怎么办？
f (i )
S第i个矩形
S第i个矩形
1 n
f (i )
y f (x)
第i个小曲边梯形
i-1 i
n i n
S黄色部分 S第1个黄色矩形 S第2个黄色矩形 ... S第n个黄色矩形
1 n
f (1)
1 n
f (2 ) ...
1 n
f (n )
n i1
1 n
f (i )
lim S曲边梯形
y
—— 分成很窄的小曲边梯形，然后用矩形面积代后求和。
y f (x)
y
x
Oa b
y f (x)
—— 以直代曲
Oa
bx
例1.求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积.
解:把底边[0,1]分成n等份,然后在每个分点作底边的垂线, 这样曲边三角形被分成n个窄条, 用矩形来近似代替,然后把这些小矩形的面积加起来, 得到一个近似值:
12 22 L i2 L n2
n3 n3
n3
n3
1 22 32 L n2
n3
4、取极限
S曲边梯形 S黄色部分
1 22 32 L n2

定积分的几何意义曲边梯形面积的代数和如图

积
分思路：把整段时间分割成若干小段，每小段上
的概
速度看作不变，求出各小段的路程再相加，便
念得到路程的近似值，最后通过对时间的无限细
分过程求得路程的精确值．
mathsoft
（1）分割 T0 t0 t1 t2 tn1 tn T1
第
ti ti ti1
si v( i )ti
则Ai f (i )xi
n
step3: 求和 A f (i )xi
i 1
mathsoft
step4 : 取极限当分割无限加细,即小区间的最大
长度 max{x1 , x2 ,xn }
n
第一
趋近于零
(

0) 时，A
lim Biblioteka 0 i1f(i )xi

sinxdx0

mathsoft
例3
利用定义计算
1
exdx 0
解：1。将[0，1]n等分，
一确定的极限I ，我们称这个极限I 为函数 f ( x)
节在区间[a,b]上的定积分，记为
定积分的
积分上限
b a
f ( x)dx

I
lim 0
n i 1
积分和
f (i )xi
概
积分下限
念
被
被
积 [a,b] 积分区间
积
积
分
函数
表达
变量
积分符号
式
mathsoft
A
1
节定 0a
bX
a
A2
b
a
b
积
分的

1.4.1曲边梯形的面积与定积分(上课用)

2、一般函数定积分的定义设f(x)是定义在区间[a，b]上的一个函数，在闭区间[a，b]上任取n－1个分点
a x0 x1 xi 1 xi xn b
把[a，b]分成 n个小闭区间，其长度依次为△x=xi+1－xi，i=0，1，2，„，n－1，记 λ为这些小区间长度的最大者，当λ趋近于0 时，所有小区间的长度都趋近于0，在每个 i [ xi 1 , xi ] 小区间内各取一点，
i 1 2 ) 为左端点的纵坐标 ( n 1
高，△x= 形，
n
为底作小矩
x O
1
于是图中曲线之下小矩形面积依次为
1 1 2 1 2 2 1 n 1 2 1 0 , ( ) , ( ) , , ( ) , n n n n n n n
2
所有这些小矩形的面积的和为
1 1 2 1 2 2 1 n 1 2 1 Sn 0 ( ) ( ) ( ) n n n n n n n
3.定积分的几何意义：
xa、xb与 x轴所围成的曲边梯形的面积。
求由抛物线y=x2与直线x=0、x=1、 1 y=0所围成的平面图形的面积．
B
四步曲：
曲边三角形
1°分割— 化整为零 1 2°近似代替— 以直代曲 O A x 0 x 1 x ? 3°求和 — 积零为整 1 1 2 n 1 0, , , ,, ,1 4°取极限(逼近) — n n n n 精益求精
2 kb 当n→+∞时，上式右端趋近于 2
于是得到弹簧从平衡位置拉长b所做的功为
kb W lim Wi n 2 i 0
n 1 2
以上两个实际问题，一个是求曲边梯形的面积，一个是求变力所做的功，虽然实际意义不同，但解决问题的方法和步骤是完全相同的，都归结为求一个函数在某一闭区间上的和式的极限问题.

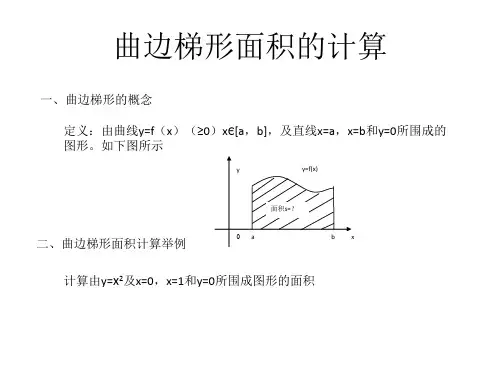
曲边梯形面积的计算

y
y=x2
Δ si
（2）在每个小区间上选取右端点的涵数值xi2 作为高，小区间的长度Δxi作用为宽，求出每 0 个小区间上对应图形面积的近似值（即以矩形面积代替） Δsi≈xi2Δxi=(i/n)2(1/n) ， i=1，2，…，n
Байду номын сангаасxi-1
xi
1
x
（3）把所有的近似值累加起来便得到整个曲边梯形面积的近似值
i 2 1 s si x xi ( n ) n i 1 i 1 2 i i 1 n n n 1 n3
(12 22 n 2 )
n ( n 1)( 2 n 1) 6 n3
（4）可以看到近似值会随着n的增大而逐渐趋于精确值，所以曲边梯形的面积
i 2 s lim x xi lim ( n ) n i 1 2 i n i 1 n n 1 n
)( 2 n 1) lim n ( n 1 6 n3 n
1 3
三、方法的一般化
（1）将区间[a，b]任意划分为n个小区间： [x0，x1]，[x1，x2]，…，[xn-1，xn]，Δxi=xi-xi-1， i=1，2，…，n，其中x0=a，xn=b （2）在[xi-1，xi]上任取一点ξi，以f（ ξi ）作为高，Δxi作为宽得到第i个小区间上对应的小曲边梯形面积Δsi的近似值，即
1 i n i
s lim f ( i ) xi
0
i 1
n
Δsi≈ f（ ξi ） Δxi ， i=1，2，…，n
y
y=f(x)
f(ξ i)
0
a
xi-1 ξ
i
xi
b
x
（3）将上述所有近似值累加起来得到整个曲边梯形的面积s的近似值，即

(精选)曲边梯形的面积

图1.5 3
曲边梯形面积的近似值.可以想象,随着拆分越来越
细,近似程度就会越来越好. 也即: 用化归为计算矩
形面积和逼近的思想方法求出曲边梯形的面积.我
们通过下面步骤来具体实施这种方法.
6
思考2：设想把该曲边梯形分作若干个小
梯形，具体如何操作？
1、分割 y
在区间0,1上间隔地插入n 1 y x2
2

2
32 3

112 3
m2
.
22
小结作业
1.用极限逼近原理求曲边梯形的面积，是一种“以直代曲” 的思想，它体现了对立统一，量变与质变的辨证关系.
2.求曲边梯形的面积的基本思路是：把曲边梯形分割成n 个小曲边梯形→用小矩形近似替代小曲边梯形→求各小矩形的面积之和→求各小矩形面积之和的极限.
3. 上述求曲边梯形面积的方法有一定的局限性，如果用一般方法不能求出各小矩形的面积之和，则得不到曲边梯形的面积.
在区间［0，2］上等间隔地插入n-1个
点，将区间［0，2］等分成n个小区间：
［0, 2］，［2 , 4］,［, 2n 1 ,2］
n
nn
n
n
则S＝ Si iБайду номын сангаас1
记第i个区间为［2i 1，2i］(i 1,2,n)，
nn
其长度为 x 2i 2i 1 2
nnn
分别过上述n-1个分点作x轴的垂线，从而得到n个小曲边
y＝x2
1x
4
可以发现,图1.5 2中的曲边梯形与" 直边图形" 的主要区
y y x2
别是,前者有一边是曲线段,
而" 直边图形" 的所有边都是

高中数学(新课标)选修2课件1.5.1-2曲边梯形的面积

＝n＋i－n1n＋i.
(3)求和
小曲边梯形的面积和
n
n
Sn＝ ΔSi＝
i＝1
i＝1
n n＋i－1n＋i
＝nn1－n＋1 1＋n＋1 1－n＋1 2＋…＋n＋1n－1－n＋1 n＝nn1－21n＝12. (4)取极限当 n 趋向于无穷大，即 Δx 趋向于 0 时，Sn 越来越趋向于 S，
从而有 linm→∞Sn＝12，所以由直线 x＝1，x＝2，y＝0 和曲线 y＝x12围成
＝－n13[02＋12＋22＋…＋(n－1)2]＋n12[0＋1＋2＋…＋(n－1)] ＝－n13·16n(n－1)(2n－1)＋n12·nn2－1 ＝－－n62n＋2 1＝－16n12－1.
(4)取极限
当分割无限变细，即 Δx 趋向于 0 时，n 趋向于∞，此时
－16n12－1趋向于
S.从而有
S＝li m n→∞
跟踪训练 1 求由直线 x＝1，x＝2，y＝0 及曲线 y＝x12围成图形的面积 S.
解析：(1)分割在区间[1,2]上等间隔地插入 n－1 个点，将它分成 n 个小区间为n＋ni－1，n＋n i(i＝1,2，…，n)，其长度为 Δx＝1n.分别过上述 n －1 个点作 x 轴的垂线，把曲边梯形分成 n 个小曲边梯形，它们的面积记 ΔSi(i＝1,2，…，n)． (2)近似代替在区间n＋ni－1，n＋n i上，当 n 趋向于无穷大，即 Δx 趋向于 0 时，我们用小矩形面积近似地代替 ΔSi，则有 ΔSi≈n＋i－n12n＋i·1n
状元随笔曲边梯形面积的求解过程，其实可以用下面的表
述：
(1)将区间[a，b]分割，等分为 n 个小区间，每个小区间的长度为 Δx＝b－n a；
(2)“近似代替”中每个小区间上函数 f(x)的值可任意取一点 ξi∈[xi －1，xi]，用 f(ξi)来代替，不影响极限的值．为了计算方便，可以取区间的一些特殊点，如区间的端点或中点等；

6.1.1定积分概念

练习题答案
一、1、lim f ( i )x i ；
0
i =1 n
2、被积函数,积分区间,积分变量； 3、介于曲线 y = f ( x ) , x 轴 ,直线 x = a , x = b 之间各部分面积的代数和； b 4、 dx .
a
1 3 3 二、 ( b a ) b a . 3 1 2 2 三、 ( b a ) . 2 五、88.2(千牛).
表示成定积分.
思路：
lim f (i )xi = f ( x )dx
b 0 i =1 a
n
1 注：一般考虑 a, b = 0,1 , n等分,xi = . n n 1 1 lim f (i ) = f ( x )dx 0 n n i =1
1 2 ( n 1) lim sin sin sin n n n n n
三、存在定理
定理1 当函数 f ( x ) 在区间[a , b]上连续时，
称 f ( x ) 在区间[a , b]上可积.
定理2 设函数 f ( x ) 在区间[a , b]上有界，
且只有有限个间断点，则 f ( x ) 在
区间[a , b ]上可积.
四、定积分的几何意义
f ( x ) > 0, f ( x ) < 0,
i =1 n
•如果当0时, 上述和式的极限存在, 且极限值与区间[a, b] 的分法和i的取法无关, 则称此极限为函数f(x)在区间[a, b]上
的定积分, 记为 f ( x)dx , a
b
b
即
n i=1
lim a f (x)dx = 0 f (i )xi
积分上限

曲边梯形的面积市公开课金奖市赛课一等奖课件

续曲线y=f(x)，直线x=a、x=b及x轴所围成图
形叫做曲边梯形。
y
y=f (x)
x=a
Oa
x=b
bx
第4页
思考： y
y = f(x)
A1
Oa
b
x
用一个矩形面积A1近似代替曲边梯形面积A，
得 A A1.
第5页
y = f(x) y
A1 Oa
A2
b
x
用两个矩形面积近似代替曲边梯形面积A，得 A A1+ A2
第6页
y = f(x) y
A1
A2
A3
A4
Oa
b
x
用四个矩形面积近似代替曲边梯形面积A，得 A A1+ A2+ A3+ A4
第7页
y = f(x) y
A1
Ai
An
Oa
bx
将曲边梯形分成 n个小曲边梯形，并用小矩形面积代替
小曲边梯形面积，于是曲边梯形面积A近似为
A A1+ A2 + + An
数，在闭区间[a，b]上任取n－1个分点
a x0 x1 xi1 xi xn b
把[a，b]分成 n个小闭区间，其长度依次
为△x=xi+1－xi，i=0，1，2，…，n－1，记 λ为这些小区间长度最大者，当λ趋近于0时，
所有小区间长度都趋近于0，在每个小区间
内各取一点，
i [xi1, xi ]
a,b内可积分，则f(x) g(x)也在此区间内
可积分，且 b a
f(x)
g
(
x)
dx
b
f (x)dx
a
b

15定积分(N-L先讲)

3
4、变限定积分的导数
设变上限积分 ( x ) f (t )dt，则
a x
( x ) ( f (t )dt ) f ( x )
a
x
证明：不妨设f(t)的一个原函数为F(t)，则有
( x ) ( f (t )dt ) ( F (t ) a )
x a
二、定积分的分部积分法
例4

0
1
xe 2 x dx
x
e
0

1
2x
1 2x e 2
0

0
1 2x e 4
1 2x 1 2x xe e 1 xe dx 4 2 1 1 0 1 1 2 2 0 e (1)e e 4 2 4
y
在每个小区间[ xi 1 , xi ] 上任取一点 i，
o a
x1
x i 1 i xi
xn1 b
x
以 [ xi 1 , xi ]为底， f (i ) 为高的小矩形面积为
Ai f ( i )xi
曲边梯形面积的近似值为
A f ( i )xi
i 1
n
当分割无限加细 ,即小区间的最大长度
a
a
例如

2
2
x 3 cos xdx 0
f ( x) x 3 cos x为连续的奇函数
连续或逐段连续的偶函数在对称区间上的定积分为一半区间上积分的2倍，即
设f ( x )为连续或逐段连续的偶函数，则

a
a
f ( x )dx 2 f ( x )dx
0
a
例3、 x 2 sin x 1 dx

定积分

0 i 1
n
b
n
n
0 i 1
a f ( x )dx a g( x )dx.
此性质可以推广到有限项代数和的情况
b
b
（3）（定积分的可加性）若 f ( x ) 在 [a, c],[c, b] 上都可积
则有

b a
f ( x )dx

c a
f ( x )dx f ( x )dx
e
1 i lim ln f n n n i 1

n
e
i1 lim ln f n n n i 1

n
f ( x)
在 [0,1] 上连续，且取正值，
所以 ln f ( x ) 在 [0,1]上有意义且取可积，
i 1 i 对 [0,1] 进行分割x i , 则 x i , 取 i n n n
0

2 e
0
x
dx 2xdx, e dx 0 xdx.
x
2
于是
0
2
性质5的推论：
（1）如果在区间[a , b]上 f ( x ) g( x ) ，
则 a f ( x )dx
b
a g( x )dx .
b
(a b)
则
b c
c
c
b
c
a b c, f ( x )dx
c
a f ( x )dx a f ( x )dx b f ( x )dx
a f ( x )dx c f ( x )dx.
b
（定积分对于积分区间具有可加性）
性质4
a 1 dx a
b a
b

元素法

xn1 b
x
.
.
1. 曲边梯形的面积 f ( i) y y=f (x)
元素法
1分割：化整为零 2近似：以直代曲 (以常代变) S i f ( i )xi 3求和：积零为整
S f ( i )x i
i 1 n
.
分法越细，越接近精确值
o
a
x i i x i 1
x
.
4取极限
.
o
a
a
x
来看动点的慢动作
8. 心形线 (圆外旋轮线)
一圆沿另一圆外缘无滑动地滚动，动圆圆周上任一点所画出的曲线。
y
o
a
a
x
2a
来看动点的慢动作
.
8. 心形线 (圆外旋轮线)
一圆沿另一圆外缘无滑动地滚动，动圆圆周上任一点所画出的曲线。
y
P
r = a (1+cos )
0 2
曲线可以看作这种点的轨迹：从极点射出半射线动点在射线上作等速运动同时此射线又绕极点作等速转动
0
r
.
请问：动点的轨迹什么样？
再看一遍
13.
阿基米德螺线 r =a
0
r
.
13.
阿基米德螺线 r =a
0
r
.
13.
阿基米德螺线 r =a
0
r
.
13.
阿基米德螺线 r =a
这里从 0
+
0 r 2a
o

r

x
2a
.
例6. 计算心形线
面积 . 解:
2 4 4 cos a 0 2
所围图形的

高中数学曲边梯形面积公式

曲边梯形的面积
石春蕊
扇形从直观上看类似三角形（一边为曲边），扇形的面积公式，从形式上看类似三
角形的面积公式。

因此，我们可以把扇形看作曲边三角形，把弧长l看作底，半径r看作底边上的高。

同样地，如图1所示，两个同心圆被两条半径截得的两段弧、与两条半径所围成的图形（称为扇环）。

从形式上看类似梯形（上、下底为曲边），不妨把它看作曲边梯形，把，
看作曲边梯形的上下底，两圆半径差R－r看作曲线梯形的高。

那么曲边梯形的面积是否符合梯形的面积公式
图1
设大小两圆的半径分别为R和r，两段弧所对的圆心角为n°，则有
，①
，②
①÷②，得
即
所以
因此，曲边梯形的面积同样适合一般梯形的面积公式，即
其中分别为曲边梯形的上下底，即两个扇形的弧长，h为曲边梯形的高，即两个同心
圆的半径之差
有了这个公式，用它来求解相关的问题是既快又准，请看以下两例。

例1. 如图2所示，，，且，求。

图2
解：由曲边梯形面积公式知
注：若用常规方法解之，可看出上述解法十分快捷。

1.5.1曲边梯形的面积

间 xi1 , xi 的长度 xi xi xi1 ，
第二步：近似代替，“以直代曲”。用矩形的面积近似代替小曲边梯形的面积，求出每个小曲边梯形面积的近似值．
3．求曲边梯形面积的四个步骤:
第三步：求和．
第四步：取极限。说明：1．归纳以上步骤，其流程图表示为：
分割→近似代替→求和→取极限 2．最后所得曲边形的面积不是近似值，而是真实值
在区间

i
n
1
,
i n
上，可以认为函数
f
x
x2 的值
变化很小，近似的等于一个常数，不妨认为它近似
的等于左端点
i
1 n
处的函数值
f

i
1 n
，从图形上
看，就是用平行于 x 轴的直线段近似的代替小曲边
梯形的曲边（如图）．
这样，在区间
i
1 n
,
i n
问题转化为求“直边图形”面积的问题？。
分析：曲边梯形与“直边图形”的主要区别：曲边梯形有
一边是曲线段，“直边图形”的所有边都是直线段．“以直
代曲”的思想的应用．
y
y
y
y
y x2
x
x
x
1x
1x
O
0.2 0.4 0.6 0.8 1
x
把区间 0 ,1 分成许多个1 小x 区间，进而把区边梯形拆为一些
S

lim
n
Sn

lim
n
n i 1
f
(i
1) n
1 n

lim 1 (1 n 3
1 )(1 n
1) 2n

1.5 .1曲边梯形的面积

方法总结：我们能否得到求一般性曲边梯形的面积
方法（如下图所示）？一般地，对如图所示的曲边梯形，我们也可采用分
割、近似代替、求和、取极限的方法，求出其面积。
求曲边梯形面积的“四步曲”： 1°分割 2°近似代替化整为零以直代曲
3°求和 4°取极限
积零为整刨光磨平
探究点二问题
求变速运动的路程
利用导数我们解决了“已知物体运动路程与时间的关
系，求物体运动速度”的问题．反之，如果已知物体的速度与时间的关系，如何求其在一定时间内经过的路程呢？
答物体以速度v做匀速直线运动时，经过时间t所行驶的路程为s＝vt.如果物体做变速直线运动，与求曲边梯形面积类似，我们采取“以不变代变”的方法，把求变速直线运动的路程问题，化归为求匀速直线运动的路程问题．
i＝1 n
小区间，
(2)近似代替
2i 取ξi＝ n (i＝1,2，„，n)．于是 2i 2i 2 2 ΔSi≈ΔS′i＝v( n )·Δt＝[3( n ) ＋2]· n 24i2 4 ＝ n3 ＋n(i＝1,2，„，n)． (3)求和 Sn＝ ΔS′i＝
i＝1 n n i＝1
本课时栏目开关
i－1 1 1 n i－1 2 Sn＝ f(1＋ n )· ＝n [(1＋ n ) ＋2] n i＝1 i＝1
n 2 1 n i－1 2i－1 ＝n [ n2 ＋ n ＋3] i＝1
1 1 2 2 2 1 2 ＝n{3n＋ 2[0 ＋1 ＋2 ＋…＋(n－1) ]＋n[0＋2＋4＋6＋…＋ n n－12n－1 n－1 2(n－1)]}＝3＋＋ n . 6n 2
于是所求平面图形的面积近似等于
本课时栏目开关
1 36 49 64 81 1 255 (1＋＋＋＋ )＝ × ＝1.02. 10 25 25 25 25 10 25

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ba n
f
i
即时小结
以上计算曲边三角形面积的过程可以用流程图表示：
分割
近似代替
求和
逼近
y
y
y
y
O
xO
xO
xO
x
一个案例两种思想三个方案四个步骤
课堂小结
求一个具体曲边梯形的面积 “以直代曲”和“无限逼近”思想方案一、方案二、方案三分割、近似代替、求和、求极限
• 有位成功人士曾说过：“做事业的过程就是在求解一条曲线长度的过程。每一件实实在在的小事就是组成事业曲线的直线段。”想想我们的学习过程、追求理想的过程又何尝不是这样？希望大家能用微积分的思想去学习、去做事！
观察以下演示，注意当分割加细时，矩形面积和与曲边梯形面积的关系。
观察以下演示，注意当分割加细时，矩形面积和与曲边梯形面积的关系。
返回
深入思考
• 通过动画演示我们可以看出，n越大，区间分的越细，各个结果就越接近真实值。为此，我们让n无限变大，这就是一个求极限的过程。
两个结论
• （1）在分割时一定要等分吗？不等分影响结果吗？
y x2 所围成的平面图形的面积 S？ y
y x2
o
1x
思维导航
看看怎样求出下列图形的面积?从中你有何启示？
y
y
A
A
∟
∟
o
B
x
o
B
x
不规则的几何图形可以分割成若干个规则的几何图形来求解
思维导航
-----割圆术
魏晋时期的数学家刘徽的割圆术
“…割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣…”
曲边梯形的面积
情境创设
金门大桥（美国）
概念形成曲边梯形：在直角坐标系中，由连续曲线
y=f(x)，直线x=a、x=b及x轴所围成的图形叫
做曲边梯形。
y
①、只有一边是曲线 ②、其他三边是特殊直线
y=f (x)
x=a
Oa
x=b
bx
案例探究
如何求由直线 x 0, x 1, y 0 与抛物线
的垂线, 这样[0,1]区间
分成n个小区间：0,
1 n
,

1 n
,
2 n
,

n
1 n
,1
记第i个区间为 i
1, n
i n
i
1,2,
,
n
y
长度: x i i 1 1
y=x2
nn n
对应的小曲边梯形面积为△Si
Sn S1 S2 Si Sn
1.在分割时，不管采用等分与不等分，结果一样。
• （2）在近似代替时用小区间内任一点处的函数值影响结果吗？
2. 在近似代替时，用小区间内任一点处的函数值作为近似值，结果也是一样的。
• （3）总结一般曲边梯形面积的表达式？
归纳概括
一般曲边梯形的面积的表达式
S
n
lim n i1
O 1 2 i 1 i n 11 x
n n nn n
案例探究
2、近似代替(以直代曲）思考3：对每个小曲边梯形
y
如何“以直代曲”？
y=x2
f ( i ) ( i )2 nn
f (i 1) (i 1)2
n
n
f ( i ) ( i )2 nn
O i 1 i
1x
nn
方案. 方案.. 方案… 方案….
——刘徽
刘徽的这种研究方法
对你有什么启示?
思维导航
-----割圆术
魏晋时期的数学家刘徽的割圆术
“…割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣…”
——刘徽
刘徽的这种研究方法
对你有什么启示?
思维导航

-----割圆术
割圆术：刘徽在《九章算术》注中讲到
“…割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣…”
——刘徽
以“直”代“曲” 无限逼近
刘徽的这种研究方法对你有什么启示?
案例探究
如何求由直线 x 0, x 1, y 0 与抛物线
y x2 所围成的平面图形的面积 S？
思考1：怎样“以直代曲”？
y
能整体以“直”代“曲吗？
思考2：怎样分割最简单？
y x2
o
1x
案例探究
1、分割把底边[0,1]分成n等份, 在每个分点作底边
深入思考
怎样使各个结果更接近真实值？
观察以下演示，注意当分割加细时，矩形面积和与曲边梯形面积的关系。
观察以下演示，注意当分割加细时，矩形面积和与曲边梯形面积的关系。
观察以下演示，注意当分割加细时，矩形面积和与曲边梯形面积的关系。
观察以下演示，注意当分割加细时，矩形面积和与曲边梯形面积的关系。